sigmoid和tanh激活函数与其导数的绘图详解
激活函数(Activation Function)主要针对学习复杂的和非线性的函数,有着十分重要的作用,尤其是在多层神经网络中,应用非常广泛,对于线性函数,我们在前面说到的线性回归和Softmax回归,有兴趣的可以先熟悉下,便于后期更加理解非线性函数的实际意义。线性回归(Linear Regression)模型的构建和实现![]() https://blog.csdn.net/weixin_41896770/article/details/124192672
https://blog.csdn.net/weixin_41896770/article/details/124192672
Softmax回归模型的构建和实现(Fashion-MNIST图像分类)![]() https://blog.csdn.net/weixin_41896770/article/details/124377665
https://blog.csdn.net/weixin_41896770/article/details/124377665
这两个模型都属于线性的,对于深度学习的多层叠加,如果是线性模型,不管叠加多少层,输出还是线性的,这对于学习复杂的非线性的函数来说,就显得没辙。所以这个时候我们引入了激活函数,使得神经网络可以逼近任何的非线性函数。
常见的激活函数有(ReLU、Sigmoid、tanh[双曲正切]),这里主要讲解sigmoid和tanh以及它们的求导过程,本人将步骤画出来了,通过图片让大家看得更直观。
上面是数学公式的求导过程,现在我们分别来绘制出激活函数与对应的导数的图(MXNet已包含了这些函数的绘制,可以方便调用),大家也可以不通过MXNet框架提供的函数,自己绘图来检验上面的求导是否正确,想了解更多如何绘制图形可以参看:
Python画图(直方图、多张子图、二维图形、三维图形以及图中图)![]() https://blog.csdn.net/weixin_41896770/article/details/119798960
https://blog.csdn.net/weixin_41896770/article/details/119798960
import d2lzh as d2l
from mxnet import autograd,nd
#定义一个绘图函数
def xyplot(x,y,n):
d2l.set_figsize(figsize=(5,2.5))
d2l.plt.plot(x.asnumpy(),y.asnumpy())
d2l.plt.xlabel('x')
d2l.plt.ylabel(n+'(x)')
#sigmoid函数
x=nd.arange(-10,10,0.1)
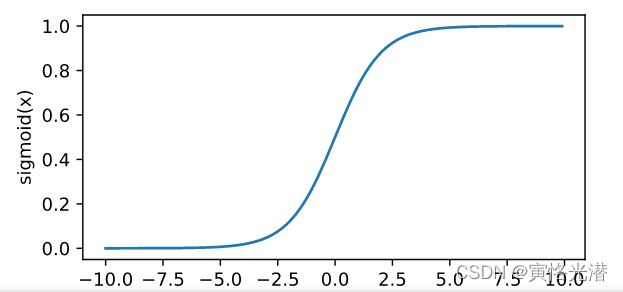
y=x.sigmoid()
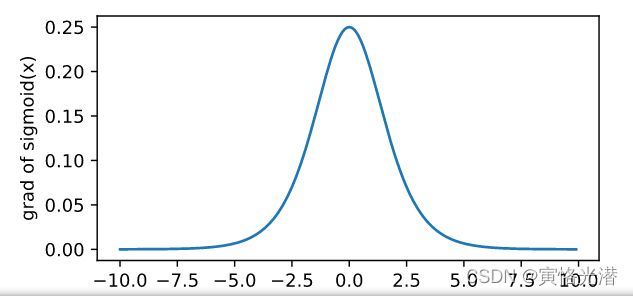
xyplot(x,y,'sigmoid')#sigmoid导数
x=nd.arange(-10,10,0.1)
x.attach_grad()
with autograd.record():
y=x.sigmoid()
y.backward()
xyplot(x,x.grad,'grad of sigmoid')#tanh函数
x=nd.arange(-10,10,0.1)
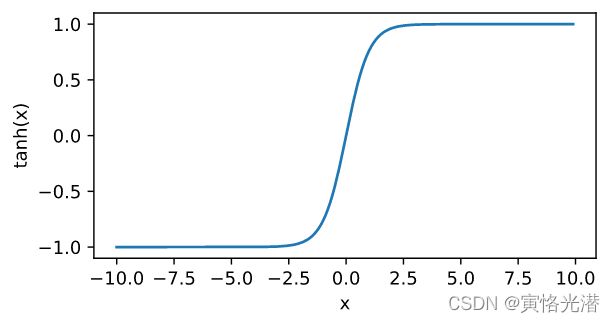
y=x.tanh()
xyplot(x,y,'tanh')tanh函数看起来和sigmoid长的特别像,区别在于tanh函数是关于原点对称
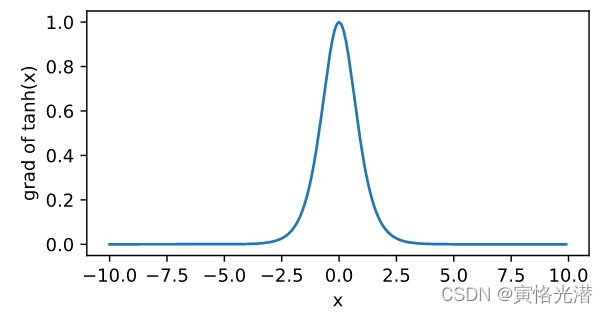
#tanh导数
x=nd.arange(-10,10,0.1)
x.attach_grad()
with autograd.record():
y=x.tanh()
y.backward()
xyplot(x,x.grad,'grad of tanh')