人工智能入门学习笔记（PyTorch）

项目：Purdue University BME595课程作业

这个项目是一位朋友向我推荐的入门学习用的，是在Github上下载的其他学生的作业，由于找不到作业要求，只有一个程序，所以每一个作业的目的，以及如何去理解这个程序都是我自己逆推出来的，包括在第二部分的卷积内容中，卷积核的目的是找出图像轮廓也是我自己猜想推理出来的，加之这是一份学习笔记，我也是初学此道，是以如果出现错误以及缺漏之处，还望诸位不吝赐教。

附参考程序：https://github.com/soumendukrg/BME595_DeepLearning

这位老哥的程序是我找了几个做对比后，相对而言readme写的较为详尽，且程序注释较多的一个。

另外，这是我第一次写博客分享学习笔记，也不太清楚是否会构成对这个项目亦或者这个老哥的程序的侵权什么的，如果有我会立刻修改。

Introduction

通过普渡大学的BME595课程作业的实例来学习人工智能的入门知识

项目包含六次课程作业和一次大作业，通过PyTorch实现

六次课程作业内容分别包括了：图像卷积、ANN、CNN

由于我本人初涉人工智能，因此会在笔记中包含大量PyTorch的方法，及最重要的人工智能的理论。

Homework01——Implementation of 2D Convolution

代码的实现目的是通过对图像进行卷积来提取输入图像的轮廓，从而掌握卷积核具有“提取特征”的作用

代码与效果图

# main.py
from conv import Conv2D
from PIL import Image
import torchvision.transforms as transforms


# 读入图片
input_image = Image.open("img0.jpg")
# 将Image图像转化为张量Tensor
input_image_tensor = transforms.ToTensor()(input_image)
# Initialize Conv2D
conv2d = Conv2D(input_channel=3, output_channel=1, kernel_size=3, stride=1)
# 对图像进行卷积操作
[num_of_ops, output_image_tensor] = conv2d.convolution(input_image_tensor)
# 此次卷积操作的操作数
num_ops = '\nThe total number of operations (multiplications and additions) for Task1 for Image is %d' % num_of_ops
print(num_ops)
# 将张量转化为numpy数组
output_image_array = output_image_tensor.numpy()
# 将数据处理后储存
conv2d.normalize(output_image_array)

# conv.py
from PIL import Image
import numpy as np
import torch


class Conv2D:
    def __init__(self, input_channel, output_channel, kernel_size, stride):
        self.input_channel = input_channel
        self.output_channel = output_channel
        self.kernel_size = kernel_size
        self.stride = stride
        # 这一卷积核对水平轮廓更敏感
        # self.kernel = torch.Tensor([[-1, -1, -1], [0, 0, 0], [1, 1, 1]])
        # 这一卷积核对铅垂轮廓更敏感
        self.kernel = torch.Tensor([[-1, 0, 1], [-1, 0, 1], [-1, 0, 1]])

    def convolution(self, input_image):
        self.input_image = input_image
        # 对于PIL Image或者numpy数组来说 其存储格式均为(Height, Width, Channel)
        # 而对于Tensor来说 其存储格式为(Channel, Height, Width)
        [channel, image_height, image_width] = self.input_image.size()
        count = 0
        # 初始化一个空的Tensor
        output_tensor = torch.zeros(image_height, image_width)
        # 将原本3*3的卷积核扩展为3*3*3的卷积核
        kernel = torch.stack([self.kernel for i in range(self.input_channel)])
        # 对图像进行卷积
        for row in range(1, image_height - 1):
            for column in range(1, image_width - 1):
            	# 边界默认为0 直接从(1,1)位置开始计算
            	# temp_tensor 用以暂存相乘后各位置的值
                temp_tensor = torch.mul(kernel, self.input_image[:, row-1:row+2, column-1:column+2])
                # output_tensor 用以存储最终计算出的值
                output_tensor[row, column] = temp_tensor.sum()
                count += 1
        # 由于此时的output_tensor为二维向量 故需人为再添加一维
        output_tensor = torch.unsqueeze(output_tensor, 0)
        num_ops = count * (torch.numel(kernel)) + count * (torch.numel(kernel) - 1)

        return(num_ops, output_tensor)

    def normalize(self, output_image_array):
        self.output_image_array = output_image_array
        for i in range(self.output_channel):
        	# 通过对每一个元素进行减去最小值后再除以最大元素和最小元素的差的方式 最终乘以255即可将图像轮廓清晰显示出来
            output_image_norm = (((self.output_image_array[i, :, :] - self.output_image_array[i, :, :].min()) / self.output_image_array[i, :, :].ptp()) * 255.0).astype(np.uint8)
            output_image_gray = Image.fromarray(output_image_norm)
            # image_name = 'out_Horizontal.jpg'
            image_name = 'out_Vertical.jpg'
            output_image_gray.save(image_name)

原图：

水平轮廓敏感图：

铅垂轮廓敏感图：

程序详解

一、读入图片并将位图转化为张量(Tensor)

通过input_image = Image.open("img0.jpg")将图片读入。

使用torchvision.transforms.ToTensor()方法将其转化为我们接下来要用来处理的张量格式。

input_image_tensor = transforms.ToTensor()(input_image)

二、对图像进行卷积

2.1 图像卷积原理

待卷积图像：

卷积核(kernel)：

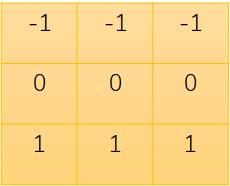
我们本例中采用卷积后图像大小与原图像一致，以及卷积时不处理边框，默认值为0。

因此我们第一个将要处理的是原图像的(1,1)处的元素。

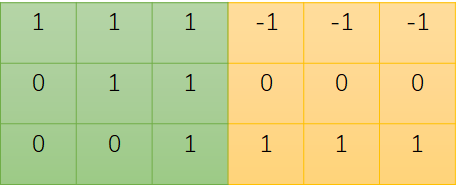
将对应位置的元素值进行相乘后得到如下图所示

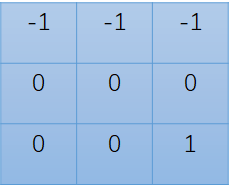
因此(1,1)处的元素应为-1 -1 -1 +0 +0 +0 +0 +0 +1 = -2 即：

如此反复处理后即可得到最终卷积后的图像。

2.2 初始化

初始化Conv2D时所需的参数共4个，分别为输入图像的通道、输出图像的通道、卷积核的尺寸和滑动步长。

输入图像的通道将会影响到卷积时对卷积核的处理。

在进行卷积前，程序先对卷积核进行了维数的扩充

kernel = torch.stack([self.kernel for i in range(self.input_channel)])

torch.stack(sequence, dim=0)将会沿一个新维度对输入张量进行连接。（dim指插入的维度）

例如：

import torch
kernel1 = torch.Tensor([[-1, -1, -1], [0, 0, 0], [1, 1, 1]])
kernel = torch.stack([kernel1 for i in range(3)])
print(kernel)
print(kernel.shape)

tensor([[[-1., -1., -1.],
         [ 0.,  0.,  0.],
         [ 1.,  1.,  1.]],

        [[-1., -1., -1.],
         [ 0.,  0.,  0.],
         [ 1.,  1.,  1.]],

        [[-1., -1., -1.],
         [ 0.,  0.,  0.],
         [ 1.,  1.,  1.]]])
torch.Size([3, 3, 3])
>>>

而滑动步长则代表了每次计算后卷积核滑动的步数，本例中采取步长为1，这样会使得输出图像与原图像大小相同，而如果将步长调整为2，则图像大小则会长宽各同比缩小2倍，即图像大小为原来的四分之一。

2.3 卷积

卷积的具体原理详见2.1

对于本例中使用到的这两种卷积核：

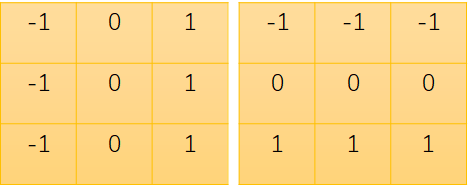
对于一个图像来说，色彩变化越多的地方，越应该是一个边界轮廓的位置，同理，颜色变化不大的时候，那么这个地方显然不会是一个轮廓所在的位置。

那么对于这两个卷积核来说，当色彩变化不大时，那么计算出的卷积后的值就越接近0，而色彩变化越大，那么他的值就离0越远，因此，可以通过这样的方式在数值上体现出一张图片的轮廓来。

for row in range(1, image_height - 1):
	for column in range(1, image_width - 1):
		temp_tensor = torch.mul(kernel, self.input_image[:, row-1:row+2, column-1:column+2])
		output_tensor[row, column] = temp_tensor.sum()
        count_mul += 1

torch.mul(input, value, out=None)表示用标量值value去乘input中的每个元素
torch.mul(input, other, out=None)表示input和other两个张量对应位置的元素相乘
torch.sum(input) → float表示将input中的所有元素加和后返回一个浮点型的值

同时由于我们此时计算出得到的output_tensor为一个二维的张量，而表示一个图像的张量应为三维(Channel, Height, Width)，又因为我们的输出图像只需要有一个通道即可，故使用output_tensor = torch.unsqueeze(output_tensor, 0)为其加上一个维度即可。

torch.unsqueeze(input, dim, out=None)将返回一个新的张量，对input张量指定的dim位置添加一个维度为一的张量

最后程序中还计算了参与整个卷积操作的操作个数，但由于我并未去做后面的图表，所以在此不再多赘述。

三、对数据处理后保存

为容易解释这一部分的数据处理，我绘制了一个简单的图形。

这是一张bmp格式的图片，因此读入之后的值只有0和1，同时为保持一致，故对这个图像在进行处理时也设置的是3通道，因此这一图形在卷积后的张量为：

数值来说是和2.1的实例是一致的，只是由于是三通道，所以计算出来的值为原来的三倍。

那么如果直接将这个张量进行输出的话，结果只会是一个在视觉上是纯黑的图片，产生这种情况的原因在于，加入只考虑黑白色彩的话，即灰度图的话，那么一张图片的颜色将从0-255分为256种灰色，0为黑色，255为白色，而我们计算出来的值相较之于255显然近乎为0，故而得到的图像一定是在视觉上分辨不出任何东西的黑色。

因此需要对张量的数值进行一些处理。

首先将张量修改为numpy数组output_image_array = output_image_tensor.numpy()

随后对数组内每一个元素进行如下处理：

1.找到整个数组的最小值numpy.min()，以及数组的最大值与最小值的差值numpy.ptp()。
2.用每个元素去减掉最小值后，再除以最大最小值的差值，最后去乘255，从而得到一个黑白分离的图像。

（这个图片由于12*12像素实在太小了，但是放大之后清晰度又实在是太差，但是原理嘛，依稀可见对角线上是黑色，而其他地方都为白色，符合我们卷积找到图像轮廓的目的）

总结

这个程序事实上还有其他的部分，比如改变卷积核的大小，以及步长之后对图像的影响。以及研究修改输出通道或者修改卷积核大小之后，对于卷积操作的操作个数的影响，并绘制函数图像，有兴趣的朋友可以去看一下我在开头写的那个在Github上的完整程序。