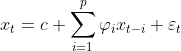机器学习——时间序列预测方法

目录

传统时序建模

自回归模型（Autoregressive model，简称AR）

移动平均模型（Moving Average model，简称MA ）

自回归滑动平均模型（Autoregressive moving average model，简称ARMA）

差分整合移动平均自回归模型（Autoregressive Integrated Moving Average model，简称ARIMA）

机器学习模型方法

深度学习模型方法

---

传统时序建模

自回归模型（Autoregressive model，简称AR）

定义

自回归模型（英语：Autoregressive model，简称AR模型），是统计上一种处理时间序列的方法，用同一变数例如x的之前各期，亦即x1至xt-1来预测本期xt的表现，并假设它们为一线性关系。因为这是从回归分析中的线性回归发展而来，只是不用x预测y，而是用x预测 x（自己）；所以叫做自回归。

其中： c是常数项；被假设为平均数等于0，标准差等于的随机误差值；被假设为对于任何的t都不变。文字叙述为：X的期望值等于一个或数个落后期的线性组合，加常数项，加随机误差。

优点与限制

自回归方法的优点是所需资料不多，可用自身变数数列来进行预测。但是这种方法受到一定的限制：必须具有自相关，自相关系数（）是关键。如果自相关系数(R)小于0.5，则不宜采用，否则预测结果极不准确。自回归只能适用于预测与自身前期相关的经济现象，即受自身历史因素影响较大的经济现象，如矿的开采量，各种自然资源产量等；对于受社会因素影响较大的经济现象，不宜采用自回归，而应改采可纳入其他变数的向量自回归模型。

移动平均模型（Moving Average model，简称MA ）

定义

移动平均模型不是在回归中使用预测变量的过去值，而是在类似回归的模型中使用过去的预测误差。

其中是白噪声，我们称之为移动平均模型，MA(q)，q阶移动平均模型，当然，我们不会也不能观测的值，所以它不是通常意义上的回归。请注意的每个值可以被认为是过去几个预测误差的加权移动平均值。

自回归滑动平均模型（Autoregressive moving average model，简称ARMA）

定义

由自回归模型（简称AR模型）与移动平均模型（简称MA模型）为基础“混合”构成。只针对平稳数据进行建模。

将预测指标随时间推移而形成的数据序列看作是一个随机序列，这组随机变量所具有的依存关系体现着原始数据在时间上的延续性。一方面，影响因素的影响，另一方面，又有自身变动规律，假定影响因素为x1，x2，…，xk，由回归分析，

其中Y是预测对象的观测值，Z为误差。作为预测对象受到自身变化的影响，其规律可由下式体现，

误差项在不同时期具有依存关系，由下式表示，

由此，获得ARMA模型表达式：

差分整合移动平均自回归模型（Autoregressive Integrated Moving Average model，简称ARIMA）

定义

非平稳时间序列，在消去其局部水平或者趋势之后，其显示出一定的同质性，也就是说，此时序列的某些部分 与其它部分很相似。这种非平稳时间序列经过差分处理后可以转换为平稳时间序列，那 称这样的时间序列为齐次非平稳时间序列，其中差分的次数就是齐次的阶。

将记为差分算子，那么有

对于延迟算子B，有

因此可以得出

设有d阶其次非平稳时间序列，那么有是平稳时间序列，则可以设其为ARMA（p，q）模型，即

其中,分别为自回归系数多项式和滑动平均系数多项式，为零均值白噪声序列。可以称所设模型为自回归求和滑动平均模型，记为ARIMA(p，d，q)。

当差分阶数d为0时，ARIMA模型就等同于ARMA模型，即这两种模型的差别就是差分阶数d是否等于零，也就是序列是否平稳，ARIMA模型对应着非平稳时间序列， ARMA模型对应着平稳时间序列。

建立模型的步骤

1. 时间序列的获取时间序列的获取可以通过实验分析获得，亦或是相关部门的统计数据。对于得到的数据，首先应该检查是否有突兀点的存在，分析这些点的存在是因为人为的疏忽错误还有有其它原因。保证所获得数据的准确性是建立合适模型，是进行正确分析的第一步保障。

2. 时间序列的预处理时间序列的预处理包括两个方面的检验，平稳性检验和白噪声检验。能够适用ARMA模型进行分析预测的时间序列必须满足的条件是平稳非白噪声序列。对数据的平稳性进行检验是时间序列分析的重要步骤，一般通过时序图和相关图来检验时间序列的平稳性。时序图的特点是直观简单但是误差较大，自相关图即自相关和偏自相关函数图相对复杂但是结果更加准确。本文先用时序图进行直观的判断再利用相关图进行更进一步的检验。对于非平稳时间序列中若存在增长或下降趋势，则需要进行差分处理然后进行平稳性检验直至平稳为止。其中，差分的次数就是模型ARIMA(p,d,q)的阶数，理论上说，差分的次数越多，对时序信息的非平稳确定性信息的提取越充分，但是从理论上说，差分的次数并非越多越好，每一次差分运算，都会造成信息的损失，所以应当避免过分的差分，一般在应用中，差分的阶数不超过2。

3. 模型识别模型识别即从已知的模型中选择一个与给出的时间序列过程相吻合的模型。模型识别的方法很多，例如Box-Jenkins模型识别方法等。

4. 模型定阶在确定了模型的类型之后，还需要知道模型的阶数，可使用BIC准则法进行定阶。

5. 参数估计对模型的参数进行估计的方法通常有相关矩估计法、最小二乘估计以及极大似然估计等。

6. 模型的验证模型的验证主要是验证模型的拟合效果，如果模型完全或者基本解释了系统数据的相关性，那么模型的噪声序列为白噪声序列，那么模型的验证也就是噪声序列的独立性检验。贝体的检验方法可利用Barlett定理构造检验统计量Q。如果求得的模型通不过检验，那么应该重新拟合模型，直至模型能通过自噪声检验。

总结：如果是处理单变量的预测问题，传统时序模型可以发挥较大的优势；但是如果问题或者变量过多，那么传统时序模型就显得力不从心了。

机器学习模型方法

这类方法以 lightgbm、xgboost 为代表，一般就是把时序问题转换为监督学习，通过特征工程和机器学习方法去预测；这种模型可以解决绝大多数的复杂的时序预测模型。支持复杂的数据建模，支持多变量协同回归，支持非线性问题。

不过这种方法需要较为复杂的人工特征过程部分，特征工程需要一定的专业知识或者丰富的想象力。特征工程能力的高低往往决定了机器学习的上限，而机器学习方法只是尽可能的逼近这个上限。特征建立好之后，就可以直接套用树模型算法 lightgbm/xgboost，这两个模型是十分常见的快速成模方法，除此之外，他们还有以下特点：

• 计算速度快，模型精度高；

• 缺失值不需要处理，比较方便；

• 支持 category 变量；

• 支持特征交叉。

深度学习模型方法

这类方法以 LSTM/GRU、seq2seq、wavenet、1D-CNN、transformer为主。深度学习中的 LSTM/GRU 模型，就是专门为解决时间序列问题而设计的；但是 CNN 模型是本来解决图像问题的，但是经过演变和发展，也可以用来解决时间序列问题。总体来说，深度学习类模型主要有以下特点：

• 不能包括缺失值，必须要填充缺失值，否则会报错；

• 支持特征交叉，如二阶交叉，高阶交叉等；

• 需要 embedding 层处理 category 变量，可以直接学习到离散特征的语义变量，并表征其相对关系；

参考链接：微信公众号深度学习初学者时间序列预测方法汇总：从理论到实践（附Kaggle经典比赛方案） (qq.com)