Pytorch：图像风格迁移

Pytorch: 图像风格迁移

Copyright: Jingmin Wei, Pattern Recognition and Intelligent System, School of Artificial and Intelligence, Huazhong University of Science and Technology

Pytorch教程专栏链接

---

本教程不商用，仅供学习和参考交流使用，如需转载，请联系本人。

Reference

Image Style Transfer Using Convolutional Neural Networks

A Neural Algorithm of Artistic Style

Perceptual Losses for Real-Time Style Transfer and Super-Resolution

图像风格迁移的主要任务是将图像的风格迁移到内容图像上，使得内容图像也具有一定的风格。

风格图像可以是艺术家的一些作品，包含艺术家的风格，也可以是经典的具有特色的照片，具有鲜明色彩。而内容图像通常来自现实世界。

利用风格迁移可以将内容图像处理为想要的风格。

常用的图像风格迁移方式

固定风格固定内容的普通风格迁移

参考文章：

Image Style Transfer Using Convolutional Neural Networks

A Neural Algorithm of Artistic Style

其思路为，把图片当做可以训练的变量，通过不断优化图片的像素值，降低其与内容图片的内容差异，并降低其与风格图片的风格差异，通过对卷积网络的多次迭代训练，能够生成一幅具有特定风格的图像。并且内容与内容图片的内容一致，生成图片的风格与风格图片的风格一致。

基于 VGG16 网络中卷积层的图像风格迁移如下：$a$ 为输入的风格图像， $p$ 为输入的内容图像，$x$ 则是表示有随机噪声生成的图像风格迁移后的图像。 ${\mathcal{L}}_{content}$ 表示图像的内容损失， ${\mathcal{L}}_{style}$ 表示图像的风格损失， $\alpha$ 和 $\beta$ 分别表示内容损失权重和风格损失权重。

使用较深层次的卷积计算得到的特征映射能够较好地表示图像内容，而较浅层次的卷积计算得到的特征映射能够较好地表示图像的风格，基于此就能通过不同卷积层的特征映射来分别度量，目标图像在风格上，以及内容上和风格图像的差异。

两个图像的内容相似性度量主要是通过在 conv4_2 层上特征映射的相似性，作为内容损失

$${\mathcal{L}}_{content}=\frac{1}{2}\sum _{i,j}(F_{ij}^l-P_{ij}^l{)}^2$$

$l$ 表示特征映射的层数， $F$ 和 $P$ 分别是目标图像和诶荣图像在读音卷积层输出的特征映射。

两个图像的风格损失并不是直接通过特征映射来比较的，而是计算 Gram 矩阵先计算出图像的风格，在进行比较。计算特征映射的 Gram 矩阵则是先将其特征映射变换为一个列向量，而 Gram 矩阵则使用这个列向量乘以其转置获得，它能更好地表示图像的风格。所以输入风格图像 $a$ 和目标图像 $x$ 使用 $A^l$ 和 $G^l$ 分别表示它们在 $l$ 层特征映射的风格表示(计算得到的 Gram 矩阵)，那么图像的风格损失可以通过下面的方式进行计算：

$$\begin{gathered} E_l=\frac{1}{4N_l^2{M}_l^2}\sum _{i,j}(G_{ij}^l-A_{ij}^l{)}^2 \\ {\mathcal{L}}_{style}=\sum _{l=0}^L{w}_l{E}_l \end{gathered}$$

$w_l$ 是每个层的风格损失的权重， $N_l$ 和 $M_l$ 对应着特征映射的高和宽。

固定风格任意内容的快速风格迁移

参考文章：

Perceptual Losses for Real-Time Style Transfer and Super-Resolution

即在普通图像风格迁移的基础上，添加一个可供训练的图像转换网络。针对一种风格图像进行训练后，可以将任意输入图像非常迅速的进行图像迁移学习，让该图像具有学习好的图像风格。

网络可看作两个部分，一部分是通过输入图像 $x$ 经过图像转换网络 $fw$ ，得到网络的输出 $\hat{y}$ ，这部分是普通风格迁移图像框架中没有的部分，普通的歉意的输入图像是随机噪声，而快速风格迁移的输入是一张图像经过转换网络 $fw$ 的输出。网络的另一部分是使用 VGG16 网络中的相关卷积层去度量一张图像的内容损失和风格损失。

在图像转换网络部分，可以分为 $3$ 个阶段，分别是图像降维部分、残差连接部分和图像升维部分。

图像降维：$3$ 个卷积层，$256\times 256\to 64\times 64$ ，通道数 $3\to 128$ 。

残差连接：$5$ 个残差块，对图像进行学习，学习如何在原图上添加少量内容，改变原图的风格。

主要思想是假设有一个网络 $M$ ，输出为 $X$ ，如果给网络 $M$ 增加一层称为性的网络 $M_{new}$ ，其输出为 $H(X)$ 。残差连接的设计思路是为了保证网络 $M_{new}$ 的性能比网络 $M$ 强，令网络 $M_{new}$ 的输出为 $H(X)=F(X)+X$ ，$M_{new}$ 在保证 $M$ 的输出 $X$ 的同时，增加了一项残差输出 $F(X)$ ，这样只要残差学习得到比"恒等于 $0$ "更好地函数，则能够保证网络 $M_{new}$ 的效果一定比网络 $M$ 好。

图像升维：输出 $5$ 个残差单元，通过 $3$ 个卷积层的操作，逐渐将其通道数从 $128$ 缩小到 $3$ ，每个特征映射尺寸从 $64\times 64$ 放大到 $256\times 256$ ，也可以使用转置卷积来完成升维部分。

针对快速风格迁移，除了使用内容损失和风格损失之外，还可以使用全变分损失，用来平滑图像。

固定风格固定内容的普通风格迁移

from PIL import Image
import matplotlib.pyplot as plt 
import numpy as np 
import requests
import time
import hiddenlayer as hl 
from skimage.io import imread

import torch
from torchvision import transforms
import torch.optim as optim
from torchvision import models

# 模型加载选择GPU
# device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
device = torch.device('cpu')
print(device)
print(torch.cuda.device_count())
print(torch.cuda.get_device_name(0))

cpu
1
GeForce MX250

准备 VGG19 网络

为了加快网络训练过程，不需要更新VGG19的参数权重，导入后将其权重冻结。

vgg19 = models.vgg19(pretrained = True).to(device)
# 不需要网络的分类器，只需要卷积和池化层
vgg = vgg19.features
# 将网络权重冻结，训练时不更新
for param in vgg.parameters():
    param.requires_grad_(False)

图像数据准备

提前控制图像的尺寸大小，为了加快风格迁移的速度。

第一个参数是读取的路径，第二第三个参数控制图像大小。

如果指定了 max_size，读取图像，若图像尺寸过大，图像会进行相应的缩小。如果指定了 shape，图像会转为 shape 大小。

def load_image(img_path, max_size = 400, shape = None):
    '''
    读取图像并保证图像的高和宽在默认情况下都小于400
    '''
    image = Image.open(img_path)
    # 如果图像尺寸过大，就进行尺寸转换
    if max(image.size) > max_size:
        size = max_size
    else:
        size = max(image.size)
    # 如果指定了图像尺寸，就将图像转化为shape指定的尺寸
    if shape is not None:
        size = shape
    # 使用transforms将图像转为张量，并进行标准化
    in_transform = transforms.Compose(
        [transforms.Resize(size), # 图像尺寸变换，短边匹配size
         transforms.ToTensor(), # 转为张量
         # 图像标准化
         transforms.Normalize((0.485, 0.456, 0.406),
                              (0.229, 0.224, 0.225))])
    # 使用图像的RGB通道，并添加batch维度
    image = in_transform(image)[:3, :, :].unsqueeze(dim = 0)
    return image

定义一个 im_covert 函数，将一张图像的四维张量转为可以使用 matplotlib 库可视化的三维数组。

def im_convert(tensor):
    '''
    将[1, c, h, w]维度的张量转为[h, w, c]的数组
    因为张量进行了标准化，所以要进行标准化逆变换
    '''
    image = tensor.data.numpy().squeeze() # 去除batch维度数据
    image = image.transpose(1, 2, 0) # 置换数组维度[c, h, w] -> [h, w, c]
    # 进行标准化逆操作
    image = image * np.array((0.229, 0.224, 0.225)) + np.array((0.485, 0.456, 0.406))
    image = image.clip(0, 1) # 将图像的取值剪切到0-1之间
    return image

# 读取内容和风格图像
content = load_image('./data/styletransfer/buildings1.png', max_size = 400)
print('content shape:', content.shape)
# 根据内容图像的宽和高设置风格图像的宽和高
style = load_image('./data/styletransfer/starry-sky1.png', shape = content.shape[-2: ])
print('style shape:', style.shape)
# 可视化内容图像和风格图像
fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (12, 5))
ax1.imshow(im_convert(content))
ax1.set_title('content')
ax2.imshow(im_convert(style))
ax2.set_title('style')
ax1.axis('off')
ax2.axis('off')
plt.show()

content shape: torch.Size([1, 3, 400, 526])
style shape: torch.Size([1, 3, 400, 526])

图像的输出特征和 Gram 矩阵的计算

输出图像在指定网络层上的特征映射，并将输出的结果保存在一个字典中。

# 用于获取图像在网络上指定层的输出
def get_features(image, model, layers = None):
    '''
    图像前向传播，并获取至顶层的特征映射
    '''
    # 将torch的VGGnet的完整映射层名称与论文中的名称相对应
    # layers参数指定：需要用于图像的内容和样式表示的图层
    # 如果layers没有指定，则使用默认的层
    if layers is None:
        layers = {'0': 'conv1_1',
                  '5': 'conv2_1',
                  '10': 'conv3_1',
                  '19': 'conv4_1',
                  '21': 'conv4_2', # 内容图层的表示
                  '28': 'conv5_1'}
    features = {} # 获取的每层特征保存在字典中
    x = image.to(device) # 需要获取特征的图像
    # model._modules是一个字典，保存着网络model每层的信息
    for name, layer in model._modules.items():
        # 从第一层开始获取图像特征
        x = layer(x)
        # 如果是layers参数指定的特征，那就保存到features中
        if name in layers:
            features[layers[name]] = x
    return features

比较两个图像是否具有相同的风格时，可以使用 Gram 矩阵来评价：

针对输入的四维特征映射，将其没一个特征映射设置为一个向量，得到一个行为d(特征映射数量)，列为h*w(每个特征映射的像素数量)的矩阵，该矩阵乘以其转置即可得到需要的Gram矩阵。

def gram_matrix(tensor):
    '''
    计算指定向量的Gram Matrix, 该矩阵表示图像的风格特征
    格拉姆矩阵最终能够在保证内容的情况下，进行风格的传输
    tensor：是一张图像前向计算后的一层特征映射
    '''
    # 获得tensor的batch_size, depth, height, width
    _, d, h, w = tensor.size()
    # 改变矩阵的维度
    tensor = tensor.view(d, h * w)
    # 计算gram matrix
    gram = torch.mm(tensor, tensor.t())
    return gram

针对内容图像和风格图像计算特征输出，并计算风格图像在每个特征输出上的 Gram 矩阵。

与此同时创建一个目标图像，该目标图像最后需要生成带有风格的内容图像，即最后的输出。

# 计算内容图像的风格表示
content_features = get_features(content, vgg)
# 计算风格图像的风格表示
style_features = get_features(style, vgg)
# 为风格图像的风格表示计算每层的Gram矩阵，使用字典保存
style_grams = {layer: gram_matrix(style_features[layer]) for layer in style_features}
# 使用内容图像的副本创建一个目标图像，训练时对目标图像进行调整
target = content.clone().requires_grad_(True) 

style_grams

{'conv1_1': tensor([[3.7243e+04, 2.7081e+04, 2.0501e+04,  ..., 2.0354e+04, 8.2865e+03,
          2.5033e+04],
         [2.7081e+04, 2.4493e+05, 8.2944e+03,  ..., 1.5048e+05, 2.6783e+04,
          7.1478e+04],
         [2.0501e+04, 8.2944e+03, 2.3988e+04,  ..., 3.0213e+02, 5.6838e+03,
          1.1918e+04],
         ...,
         [2.0354e+04, 1.5048e+05, 3.0213e+02,  ..., 5.8942e+05, 9.0042e+04,
          1.1757e+05],
         [8.2865e+03, 2.6783e+04, 5.6838e+03,  ..., 9.0042e+04, 3.7848e+04,
          2.4354e+04],
         [2.5033e+04, 7.1478e+04, 1.1918e+04,  ..., 1.1757e+05, 2.4354e+04,
          8.2842e+04]]),
 'conv2_1': tensor([[296869.7188,  49236.6797, 152745.6875,  ..., 174242.0000,
            5829.6772,  43843.0898],
         [ 49236.6797, 218713.1406,  69111.3750,  ..., 220573.0625,
           54444.7891,  33767.6641],
         [152745.6875,  69111.3750, 238272.3125,  ..., 200582.0938,
           21533.8379,  47187.3867],
         ...,
         [174242.0000, 220573.0469, 200582.0938,  ..., 818223.9375,
          113250.4219,  95792.5312],
         [  5829.6768,  54444.7812,  21533.8379,  ..., 113250.4219,
          137567.5156,  41182.2656],
         [ 43843.0898,  33767.6641,  47187.3828,  ...,  95792.5312,
           41182.2656, 100198.8750]]),
 'conv3_1': tensor([[168533.9844,  81754.6797,  13173.5088,  ...,  34211.4766,
           25890.6289,  18543.5273],
         [ 81754.6797, 222966.9688,  33485.1289,  ...,  40691.8750,
           19848.0703,  20585.1875],
         [ 13173.5088,  33485.1289,  55198.9297,  ...,  10051.2500,
            9299.3896,  20308.9043],
         ...,
         [ 34211.4766,  40691.8750,  10051.2500,  ..., 132741.6094,
           13946.0469,  19806.9453],
         [ 25890.6289,  19848.0703,   9299.3896,  ...,  13946.0469,
           63730.6484,   9267.3086],
         [ 18543.5273,  20585.1875,  20308.9043,  ...,  19806.9453,
            9267.3086,  90618.3594]]),
 'conv4_1': tensor([[3.4987e+04, 5.8576e+02, 1.1688e+02,  ..., 2.3752e+03, 1.7282e+03,
          3.0231e+03],
         [5.8576e+02, 3.3679e+03, 9.9288e+02,  ..., 2.1034e+02, 3.4831e+02,
          5.1952e+02],
         [1.1688e+02, 9.9288e+02, 5.4964e+03,  ..., 1.1056e+01, 1.0587e+03,
          2.6445e+02],
         ...,
         [2.3752e+03, 2.1034e+02, 1.1056e+01,  ..., 1.5815e+04, 9.8238e+02,
          1.1317e+03],
         [1.7282e+03, 3.4831e+02, 1.0587e+03,  ..., 9.8238e+02, 1.7580e+04,
          2.3249e+03],
         [3.0231e+03, 5.1952e+02, 2.6445e+02,  ..., 1.1317e+03, 2.3249e+03,
          1.6909e+04]]),
 'conv4_2': tensor([[23328.7051,   287.7626,  3417.6616,  ...,  1381.7507,  1568.5880,
           3186.7893],
         [  287.7626,  2798.1064,   159.8606,  ...,   291.2787,   854.2085,
            638.9219],
         [ 3417.6616,   159.8606,  8507.2031,  ...,   345.7476,   231.8674,
           2101.0503],
         ...,
         [ 1381.7509,   291.2787,   345.7476,  ..., 36131.4453, 10913.6895,
           4316.3608],
         [ 1568.5880,   854.2084,   231.8674,  ..., 10913.6895, 35504.9688,
           1602.5790],
         [ 3186.7893,   638.9219,  2101.0503,  ...,  4316.3608,  1602.5790,
          14670.7832]]),
 'conv5_1': tensor([[4.7642e+02, 1.4229e+02, 3.2485e+01,  ..., 3.5820e+00, 8.9516e+01,
          7.0400e+01],
         [1.4229e+02, 5.5915e+03, 1.2480e+02,  ..., 3.0045e+02, 3.9669e+01,
          2.7857e+02],
         [3.2485e+01, 1.2480e+02, 2.2647e+02,  ..., 1.5584e+01, 6.9174e+01,
          9.0861e+01],
         ...,
         [3.5820e+00, 3.0045e+02, 1.5584e+01,  ..., 2.9166e+02, 1.8115e+00,
          1.4014e+02],
         [8.9516e+01, 3.9669e+01, 6.9174e+01,  ..., 1.8115e+00, 3.1993e+02,
          2.5290e+01],
         [7.0400e+01, 2.7857e+02, 9.0861e+01,  ..., 1.4014e+02, 2.5290e+01,
          1.2658e+03]])}

图像风格迁移

为了训练效果，在计算风格时，针对不同层的风格特征映射 Gram 矩阵，定义不同大小的权重，此处使用 style_weights 字典法完成，并且针对最终的损失，内容损失权重 $\alpha$ 和风格损失权重 $\beta$ 分别定义为 $1$ 和 $1\times 10^6$ 。

# 定义每个样式层的权重
style_weights = {'conv1_1': 1.,
                 'conv2_1': 0.75,
                 'conv3_1': 0.2,
                 'conv4_1': 0.2,
                 'conv5_1': 0.2}
alpha = 1
beta = 1e6
content_weight = alpha
style_weight = beta

没有定义 conv4_2 的 Gram 权重，是因为该层的特征映射用于度量图像内容的相似性。

使用 Adam 优化器训练，学习率为 $0.0003$ ，每间隔 $1000$ 次迭代输出目标图像的可视化情况，并将迭代过程中每次相关损失保存在列表中。

show_every = 100 # 每迭代1000次输出一个中间结果
# 损失保存
total_loss_all = []
content_loss_all = []
style_loss_all = []
# 使用Adam
optimizer = optim.Adam([target], lr = 0.0003)
steps = 5000 # 优化时迭代的次数
t0 = time.time() # 计算需要的时间
for ii in range(1, steps + 1):
    # 获取目标图像的特征
    target_features = get_features(target, vgg)
    # 计算内容损失
    content_loss = torch.mean((target_features['conv4_2'] - content_features['conv4_2']) ** 2)
    # 计算风格损失，并初始化为0
    style_loss = 0
    # 将每层的Gram Matrix损失相加
    for layer in style_weights:
        # 计算要生成的图像的风格表示
        target_feature = target_features[layer]
        target_gram = gram_matrix(target_feature)
        _, d, h, w = target_feature.shape
        # 获取风格图像在每层的风格的Gram Matrix
        style_gram = style_grams[layer]
        # 计算要生成图像的风格和风格图像之间的风格差异，每层都有一个权重
        layer_style_loss = style_weights[layer] * torch.mean((target_gram - style_gram) ** 2)
        # 累加计算风格差异损失
        style_loss += layer_style_loss / (d * h * w)
    # 计算一次迭代的总损失，即内容和风格损失的加权和
    total_loss = content_weight * content_loss + style_weight * style_loss
    # 保留三种损失大小
    content_loss_all.append(content_loss.item())
    style_loss_all.append(style_loss.item())
    total_loss_all.append(total_loss.item())
    # 更新需要生成的目标图像
    optimizer.zero_grad()
    total_loss.backward()
    optimizer.step()
    # 输出每show_every次迭代后的生成图像
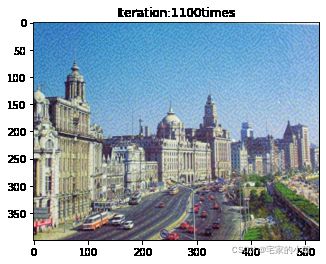
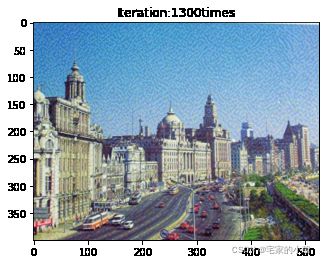
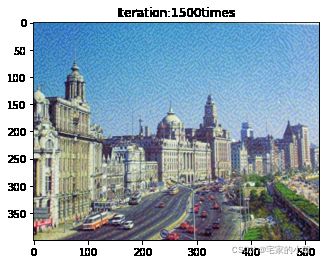
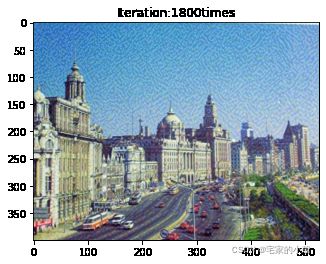
    if ii % show_every == 0:
        print('Total loss:', total_loss.item())
        print('Use time:', (time.time() - t0) / 3600, 'hour')
        newim = im_convert(target)
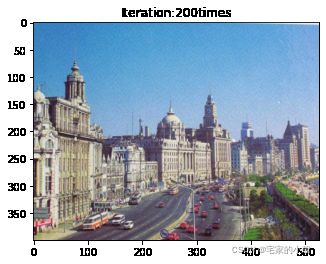
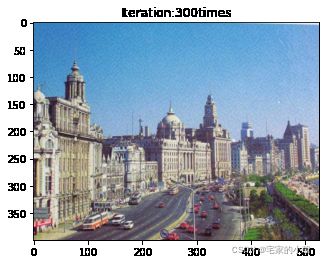
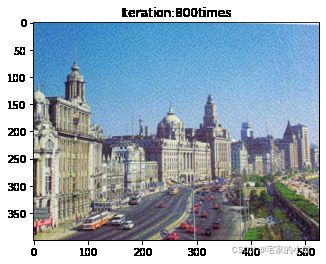
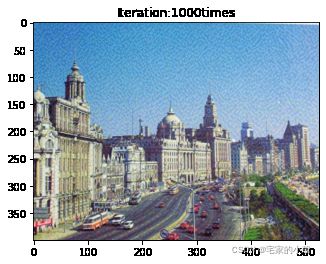
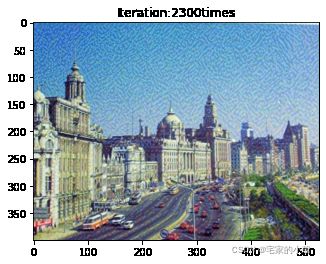
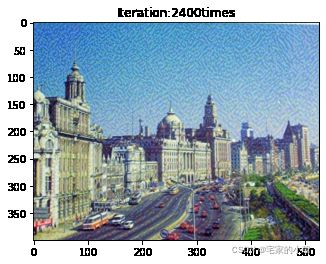
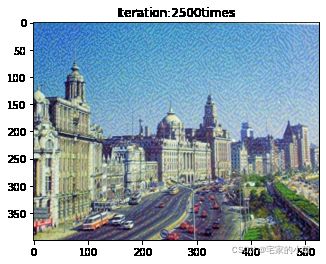
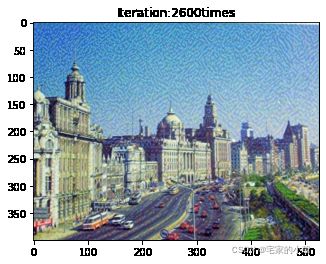
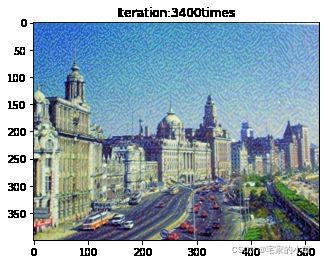
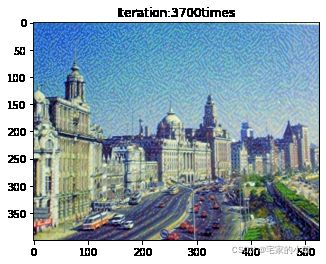
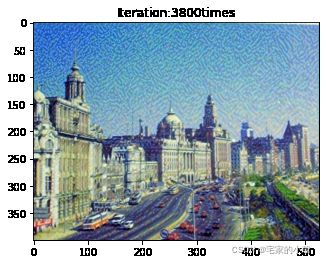
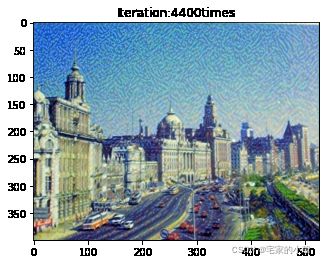
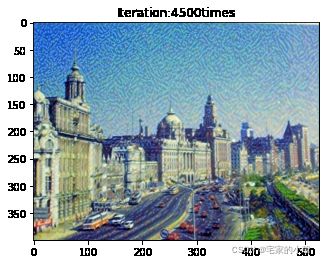
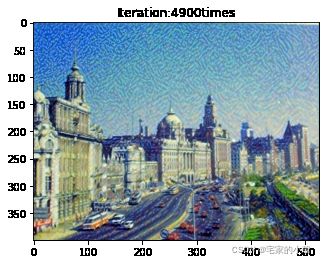
        plt.imshow(newim)
        plt.title('Iteration:' + str(ii) + 'times')
        plt.show()
        # 保存图片
        result = Image.fromarray((newim * 255).astype(np.uint8))
        result.save('./data/styletransfer/result/result' + str(ii) + '.png')

Total loss: 122845784.0
Use time: 0.09552362905608283 hour

Total loss: 94523616.0
Use time: 0.19464369164572823 hour

Total loss: 75496376.0
Use time: 0.2968603479862213 hour

Total loss: 62033356.0
Use time: 0.4009838284386529 hour

Total loss: 52134036.0
Use time: 0.5064849876695209 hour

Total loss: 44690424.0
Use time: 0.6129636422130796 hour

Total loss: 38979816.0
Use time: 0.7186389108498891 hour

Total loss: 34524896.0
Use time: 0.822829952902264 hour

Total loss: 30991986.0
Use time: 0.9157749527030521 hour

Total loss: 28144496.0
Use time: 1.0104362222221162 hour

Total loss: 25806564.0
Use time: 1.1048695998721652 hour

Total loss: 23855330.0
Use time: 1.2040331729915408 hour

Total loss: 22200796.0
Use time: 1.2968463142712912 hour

Total loss: 20776636.0
Use time: 1.3940133858389325 hour

Total loss: 19532510.0
Use time: 1.491570719215605 hour

Total loss: 18431378.0
Use time: 1.584603530433443 hour

Total loss: 17445626.0
Use time: 1.6766611027055316 hour

Total loss: 16553765.0
Use time: 1.77121149831348 hour

Total loss: 15739453.0
Use time: 1.8641047936677932 hour

Total loss: 14989285.0
Use time: 1.9569297609064313 hour

Total loss: 14294189.0
Use time: 2.053051912519667 hour

Total loss: 13646263.0
Use time: 2.15158909784423 hour

Total loss: 13039096.0
Use time: 2.245860044360161 hour

Total loss: 12466958.0
Use time: 2.3427789709303113 hour

Total loss: 11926141.0
Use time: 2.439336260954539 hour

Total loss: 11413008.0
Use time: 2.533568103114764 hour

Total loss: 10924717.0
Use time: 2.6285477293862236 hour

Total loss: 10458755.0
Use time: 2.7288781878021027 hour

Total loss: 10013593.0
Use time: 2.8237942422098583 hour

Total loss: 9587543.0
Use time: 2.9144839725229477 hour

Total loss: 9179240.0
Use time: 3.011672951777776 hour

Total loss: 8787736.0
Use time: 3.1060453993082047 hour

Total loss: 8411771.0
Use time: 3.18847301238113 hour

Total loss: 8050257.5
Use time: 3.2714244759745066 hour

Total loss: 7702339.5
Use time: 3.3536903029017977 hour

Total loss: 7367436.0
Use time: 3.436923085980945 hour

Total loss: 7045252.0
Use time: 3.5295680926243462 hour

Total loss: 6735090.0
Use time: 3.610985151529312 hour

Total loss: 6436338.0
Use time: 3.692777942617734 hour

Total loss: 6148604.0
Use time: 3.7746490195062425 hour

Total loss: 5871365.0
Use time: 3.8563965653710897 hour

Total loss: 5604487.0
Use time: 3.9382439964347418 hour

Total loss: 5347499.0
Use time: 4.020589534905222 hour

Total loss: 5100200.0
Use time: 4.10287761622005 hour

Total loss: 4862363.5
Use time: 4.193053228259086 hour

Total loss: 4633683.5
Use time: 4.289416976504856 hour

Total loss: 4414032.0
Use time: 4.39090823703342 hour

Total loss: 4203435.0
Use time: 4.492569035953945 hour

Total loss: 4001681.0
Use time: 4.573864739934604 hour

Total loss: 3808715.75
Use time: 4.657761905789375 hour

注意：

优化器使用方式为 optim.Adam([target], lr = 0.0003)，表明在优化其中，最终要优化的参数是目标图像的像素值，不会优化 VGG 网络中的权重等参数。

内容损失计算时，需提取指定层的输出，即使用 target_features[‘conv4_2’] 获得目标图像的内容表示，以及使用 content_features[‘conv4_2’] 获得内容图像的内容表示。

由于图像的风格表示的损失是通过多个层来表示，所以需要通过循环来逐层计算相关的 Gram 矩阵和风格损失。

最终的损失是风格损失和内容损失的加权和。

为了观察和保留图像风格在迁移过程中的结果，将图像每隔 $1000$ 次迭代计算后的结果进行可视化并保存到指定的文件中。

训练过程中，可视化内容损失、风格损失和总的损失如下：

plt.figure(figsize = (12, 4))
plt.subplot(1, 2 ,1)
plt.plot(total_loss_all, 'r', label = 'total_loss')
plt.legend()
plt.title('Total Loss')
plt.subplot(1, 2, 2)
plt.plot(content_loss_all, 'g-', label = 'content_loss')
plt.plot(style_loss_all, 'b-', label = 'style_loss')
plt.legend()
plt.title('Content and Style Loss')
plt.show()

​

​

目标图像初始化是内容图像，所以在训练过程中，内容损失逐渐增大，而风格损失逐渐减小，说明目标图像具有的风格就越明显。