《利用python进行数据分析》学习笔记二：Numpy模块（下）

《利用python进行数据分析》学习笔记

通用函数

通用函数，或称ufunc，是一种对数组（还是指的是ndarray数组）进行逐个元素进行标量操作，并将这些返回的结果封装进行向量化的函数
通用函数有很多种，比如较简单的逐个元素转换的一元通用函数：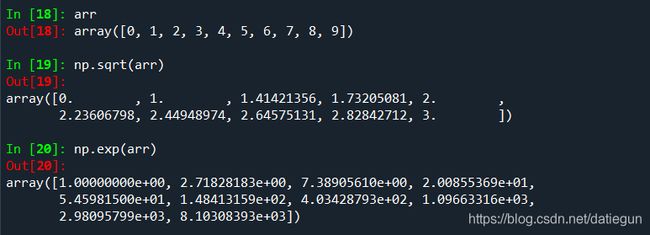
也有接收两个数组返回一个数组作为结果的二元通用函数：

也有接收多个数组，返回多个数组的函数（例子里是返回小数部分和整数部分）：

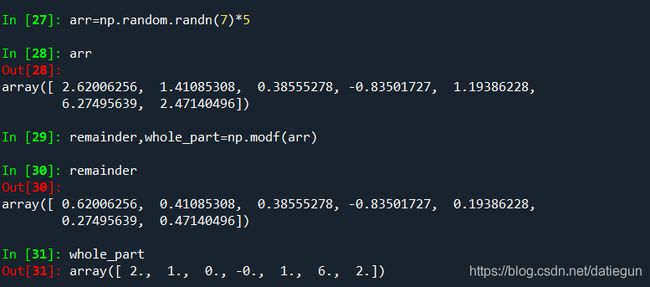
通用函数接收一个可选参数out，允许对数组按位置操作（没太理解什么意思，先把书中原文放这，例子也是，等后面看看）：

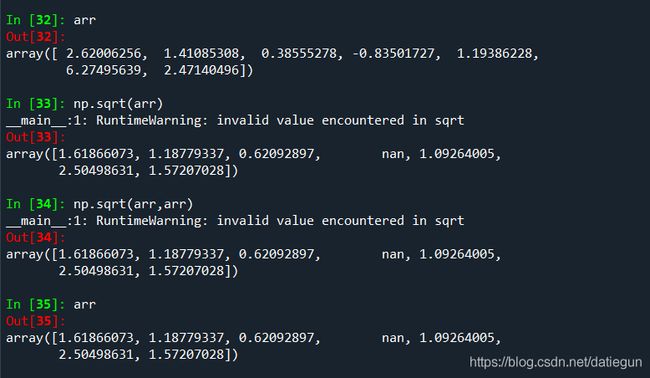
通用函数自然不止这些，还有很多，具体的见教材107页，等有需要再去查照好了；
**

使用数组进行面向数组编程

**
前面说过，Numpy可以使用数组来代替一些循环语句，这也是ndarray数组的优势之一。这种利用数组表达式来代替显式循环的方法，叫做向量化。
示例如下（np.meshgrid接收两个一维的数组，并根据两个数组的所有（x，y）对生成一个二维矩阵）：

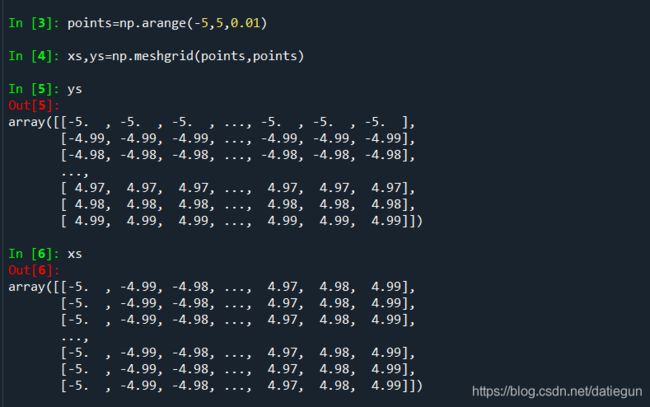
现在按照数组进行函数操作，而不用写循环语句：

图例显式是这样的（图没出来，明天检查下原因，应该是设置问题）：

**

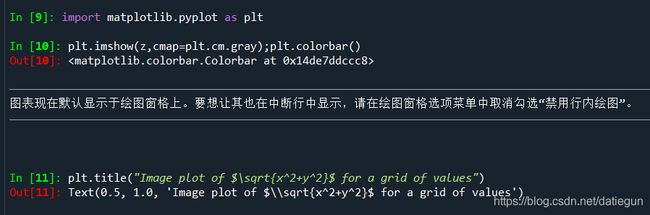
将条件逻辑作为数组操作

**
Numpy的numpy.where函数可看作三元表达式 x if condition else y的向量化版本：

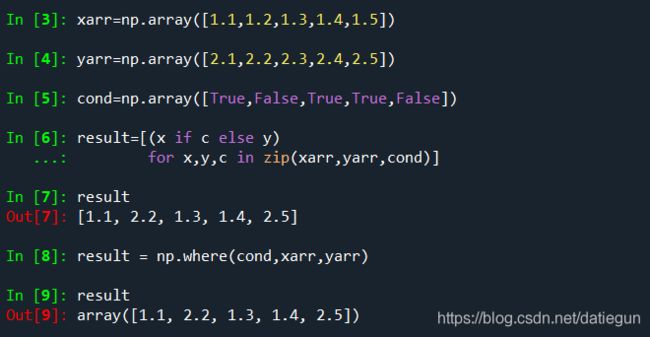
可以看到两者的结果是一致的，但后者的输出值也是一个数组；
在处理很大的数组时，使用numpy.where就有优势了，后者会快很多，而且在多维数组时，前者也就没法使用了；
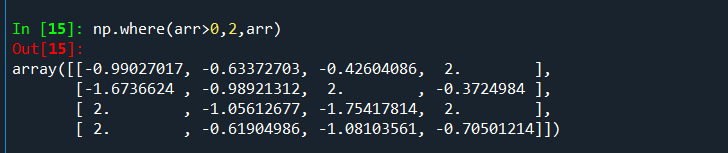
np.where的后两个参数并不需要时数组，是标量也可以，因此，这个函数的一个重要的用途就是利用一个数组来生成一个新的数组：

也可以这样数组和标量掺杂着当参数使用，即传递给numpy.where的参数既可以是同等大小的数组，也可以是标量：

**

数学和统计方法

**
许多计算整个数组统计值的函数也可以用在adarray数组中，当然也可以使用顶层的Numpy函数：

像sum、mean这类函数还有一个可接收的参数axis，表示给定的轴向（0，行向、1，列向，我暂时是这么理解的），并根据给定的轴向生成低一维度的数组：

更高维度的数组切片会按照轴向进行聚合：

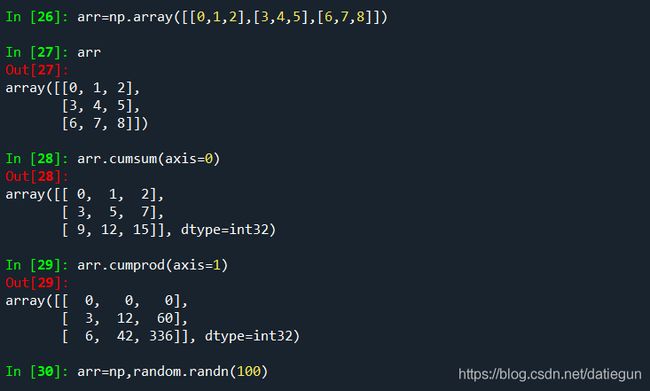
第一个是累积的和，第二个是累积的积，看清楚；

**

布尔值数组的方法

**
布尔值会被强制指定为1（True）和0（False），因此SUM
等参数也可以使用布尔值作为参数：

对于布尔值数组，有两个好用的方法：all和any，表示至少有一个，以及全部都是，和其他地方这两个函数的意思一致：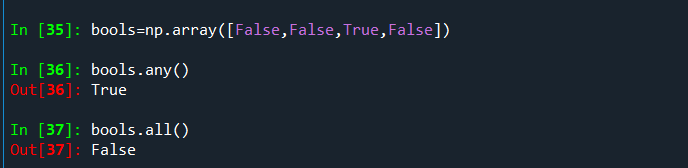
此外，这些方法也是可以用于非布尔值的数组，所有的非0元素都会被视作为True。
**

排序

**
Numpy的数组是可以使用sort方法对其进行排序的：

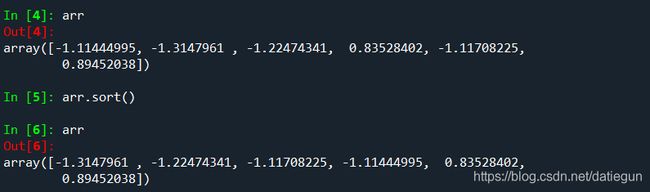
对于高维的数组，可以使用axis参数对其限制，选择排序的轴向：

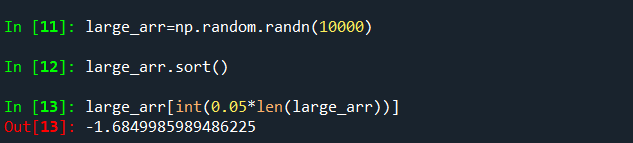
顶层的np.sort方法返回的是已经排好序的数组拷贝，而不是对原数组按位置排序（这我就不理解了，原数组的不是都被改变了么，怎么还是拷贝？），取得其中的分位数(5%)可以使用下面的方法:

**

两个重要的方法

**
np.unique：返回数组中的唯一值并排序，也就是去重后排序呗：

纯python代码当然也可以实现：

np.in1d:检查一个数组中的元素是否在另外一个数组中，返回一个布尔值数组

Numpy中其他集合函数列表：
intersect1d(x,y):交集，并排序；
union1d（x,y):并集，并排序；
setdifff1d(x,y)：差集；
setxor1d(x,y)：异或集（交集-并集）

**

使用数组进行文件输入和输出

**
这部分没什么意思，只讨论了Numpy内建的二进制格式，文本格式的内容在附录中，等后面再看好了，反正基本也会是用pandas进行存输：
存：单个数组

存：多个数组

存，并压缩文件：

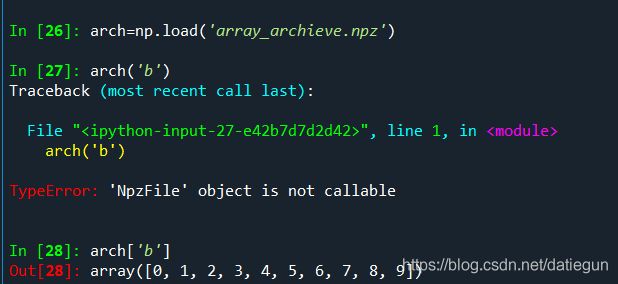
读取都是一个方法：


**

线性代数

**
因为Numpy中的数组*是逐元素进行计算的，所以矩阵的乘法需要函数dot参与：

x.dot(y)和np.dot(x,y)结果相同：
@也可以作为中缀操作符，用于矩阵点乘（这个方便一点）：
numpy.linalg拥有一个矩阵分解的标准函数集，以及一些其他的函数，使用其中的函数可以进行矩阵分解：


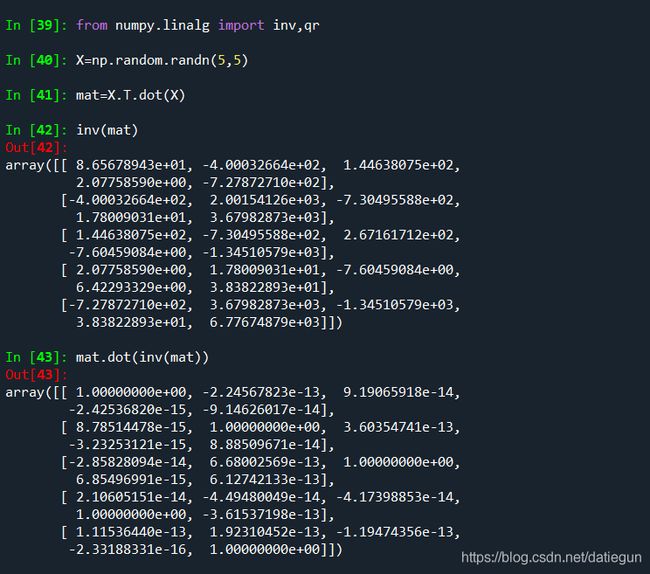
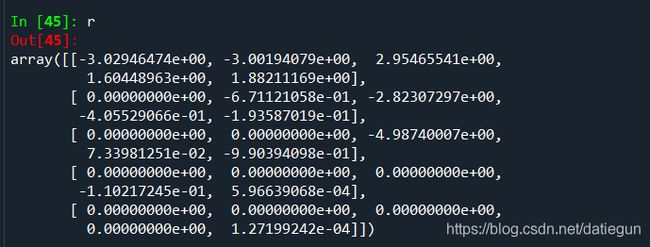
函数集中的其他函数在教材118页有列举，主要都是矩阵的运算，包括求逆矩阵、奇异值分解等内容；
**

伪随机数生成

**
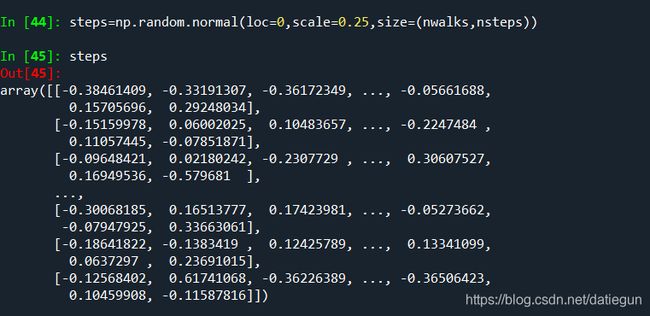
numpy.random模块可以高效得生成多种概率分布下的完整样本值数组（例：4*4的正态分布样本数组）：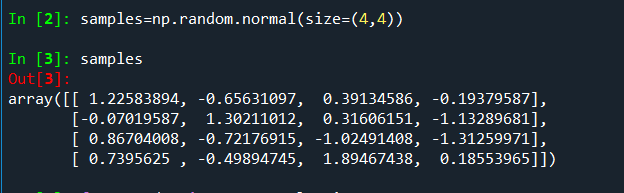
而且，相较于python内建的random模块，numpy.random在生成大型样本时的速度快了一个量级：

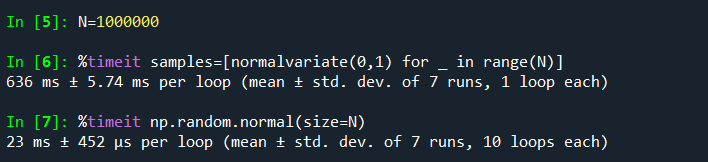
这些随机数被成为伪随计数，因为它们是由确定的算法，根据随机数生成器中的随机数种子生成的（也就是说如果种子一样，你多次生成的随机数样本也是一样的），可以通过np.random.seed来更改Numpy的随机数种子：

numpy.random的数据生成函数公用一个全局的随机数种子，如果想避免全局状态，可以使用mumpy.random.RandomState生成一个随机数生成器（是要再生成一个独立的随计数种子？），使数据独立于其他的随机数：
教材119页有部分常用的函数列表，包括从各种分布中抽取样本；

**

示例：随机漫步

**
经典的随机漫步的纯python实现如下：

可视化：

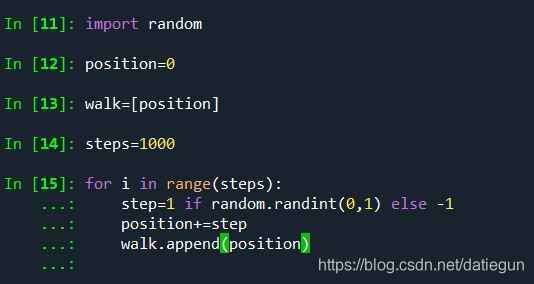
使用np.random模块模拟一次性抽取1000次掷硬币的结果，随后计算累计值也是一样的效果：

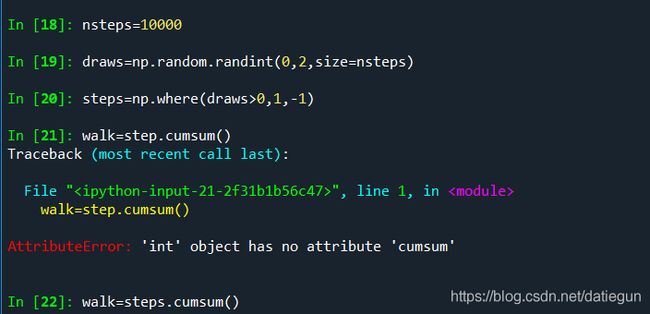
可以在漫步的轨道上提取一些统计数据：

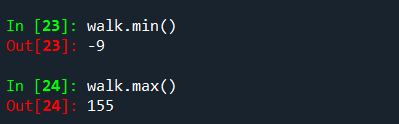
还有一种常用的数据：穿越时间，即随计漫步的某一步到达了某一个特定值例如想知道漫步中何时朝着一个方向连续走了10步，np.abs(walks)>=10可以返回一个布尔数组，但要想知道首次到达的位置，可以使用argmax函数，该函数返回布尔值数组中最大值的第一个位置（TRUE)：

**

一次性模拟多次随机漫步

**
如果输入一个2个元素的元组，就可以生成一个二维的抽样数组，再修改相应的代码，随机步数也可以相应修改：

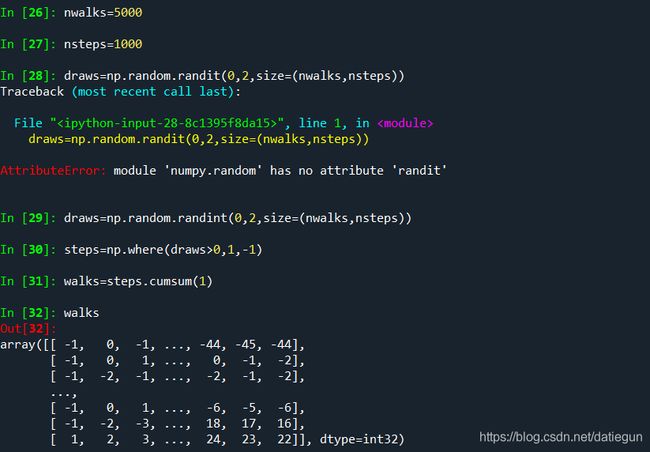
同样可以提取其中的统计数据：

如果想知道30或-30的穿越时间，因为不确定是否真的有连续走30步，可以使用ANY方法检查一下：

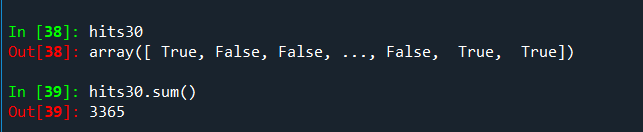
同样的使用ARGMAX函数获取具体位置（不过这里为什么要使用个mean函数？）

其他分布的随机漫步也是很容易实现的，只要换一个相应的随机数生成函数，如正态分布：