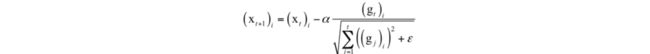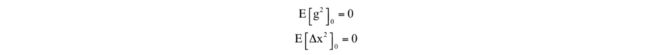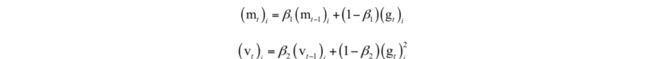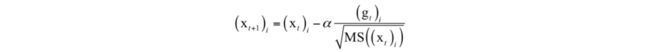梯度下降算法_理解梯度下降法
其它机器学习、深度学习算法的全面系统讲解可以阅读《机器学习-原理、算法与应用》,清华大学出版社,雷明著,由SIGAI公众号作者倾力打造。
- 书的购买链接
- 书的勘误,优化,源代码资源
导言
最优化问题在机器学习中有非常重要的地位,很多机器学习算法最后都归结为求解最优化问题。在各种最
优化算法中,梯度下降法是最简单、最常见的一种,在深度学习的训练中被广为使用。在本文中,SIGAI
将为大家系统的讲述梯度下降法的原理和实现细节问题最优化问题
最优化问题是求解函数极值的问题,包括极大值和极小值。相信所有的读者对这个问题都不陌生,在初中时我们就学会了求解二次函数的极值(抛物线的顶点),高中时学习了幂函数,指数函数,对数函数,三角函数,反三角函数等各种类型的函数,求函数极值的题更是频频出现。这些方法都采用了各种各样的技巧,没有一个统一的方案。
真正的飞跃发生在大学时,微积分为我们求函数的极值提供了一个统一的思路:找函数的导数等于0的点,因为在极值点处,导数必定为0。这样,只要函数的可导的,我们就可以用这个万能的方法解决问题,幸运的是,在实际应用中我们遇到的函数基本上都是可导的。
在机器学习之类的实际应用中,我们一般将最优化问题统一表述为求解函数的极小值问题,即:
其中x称为优化变量,f称为目标函数。极大值问题可以转换成极小值问题来求解,只需要将目标函数加上负号即可:
有些时候会对优化变量x有约束,包括等式约束和不等式约束,它们定义了优化变量的可行域,即满足约束条件的点构成的集合。在这里我们先不考虑带约束条件的问题。
一个优化问题的全局极小值
即全局极小值点处的函数值不大于任意一点处的函数值。局部极小值
并且在可行域内的所有x,有:
即局部极小值点处的函数值比一个局部返回内所有点的函数值都小。在这里,我们的目标是找到全局极小值。不幸的是,有些函数可能有多个局部极小值点,因此即使找到了导数等于0的所有点,还需要比较这些点处的函数值。
导数与梯度
由于实际应用中一般都是多元函数,因此我们跳过一元函数,直接介绍多元函数的情况。梯度是导数对多元函数的推广,它是多元函数对各个自变量偏导数形成的向量。多元函数的梯度定义为:
其中∇ 称为梯度算子,它作用于一个多元函数,得到一个向量。下面是计算函数梯度的一个例子:
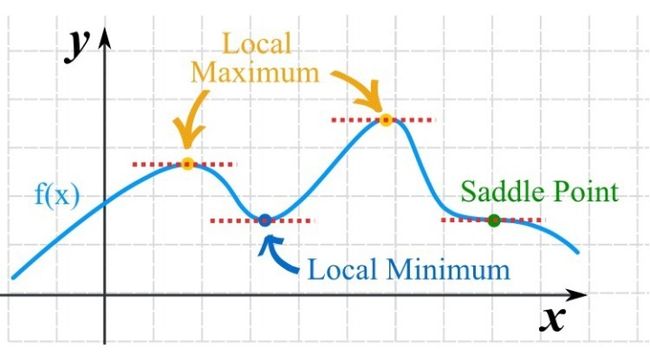
可导函数在某一点处取得极值的必要条件是梯度为0,梯度为0的点称为函数的驻点,这是疑似极值点。需要注意的是,梯度为0只是函数取极值的必要条件而不是充分条件,即梯度为0的点可能不是极值点。
至于是极大值还是极小值,要看二阶导数/Hessian矩阵,Hessian矩阵我们将在后面的文章中介绍,这是由函数的二阶偏导数构成的矩阵。这分为下面几种情况:
如果Hessian矩阵正定,函数有极小值
如果Hessian矩阵负定,函数有极大值
如果Hessian矩阵不定,则不是极值点(鞍点)这和一元函数的结果类似,Hessian矩阵可以看做是一元函数的二阶导数对多元函数的推广。一元函数的极值判别法为,假设在某点处导数等于0,则:
如果二阶导数大于0,函数有极小值
如果二阶导数小于0,函数有极大值
如果二阶导数等于0,情况不定在这里我们可能会问:直接求函数的导数/梯度,然后令导数/梯度为0,解方程,问题不就解决了吗?事实上没这么简单,因为这个方程可能很难解。比如下面的函数:
我们分别对x和y求偏导数,并令它们为0,得到下面的方程组:
这个方程非常难以求解,对于有指数函数,对数函数,三角函数的方程,我们称为超越方程,求解的难度并不比求极值本身小。
精确的求解不太可能,因此只能求近似解,这称为数值计算。工程上实现时通常采用的是迭代法,它从一个初始点
这些规则一般会利用一阶导数信息即梯度;或者二阶导数信息即Hessian矩阵。这样迭代法的核心是得到这样的由上一个点确定下一个点的迭代公式:
这个过程就像我们处于山上的某一位置,要到山底找水喝,因此我们必须到达最低点处:
此时我们没有全局信息,根本就不知道哪里是地势最低的点,只能想办法往山下走,走 一步看一步。刚开始我们在山上的某一点处,每一步,我们都往地势更低的点走,以期望能走到山底。
推导过程
首先我们来看一元函数的泰勒展开,以便于更好的理解多元函数的泰勒展开。如果一个一元函数n阶可导,它的泰勒展开公式为:
如果在某一点处导数值大于0(+),则函数在此处是增函数,加大x的值函数值会增加,减小x的值(-)函数会减小。相反的,如果在某一点处导数值小于0(-),则函数是减函数,增加x的值函数值会减小(+),减小x的值函数会增加。因此我们可以得出一个结论:如果x的变化很小,并且变化值与导数值反号,则函数值下降。对于一元函数,x的变化只有两个方向,要么朝左,要么朝右。
下面我们把这一结论推广到多元函数的情况。多元函数
这里我们忽略了二次及更高的项。其中,一次项是梯度向量∇
如果
这里的情况比一元函数复杂多了,是一个向量,
则有:
即函数值递减,这就是下山的正确方向。因为有:
在这里,||·||表示向量的模,
则能保证:
即选择合适的增量
只有当:
时
即在梯度相反的方向函数值下降的最快。此时有:
函数的下降值为:
只要梯度不为0,往梯度的反方向走函数值一定是下降的。直接用
其中
从初始点
只要没有到达梯度为0的点,则函数值会沿着序列
实现细节问题
下面我们介绍梯度下降法实现时的一些细节问题,包括初始值的设定,学习率的设定,下面分别进行介绍。
初始值的设定
一般的,对于不带约束条件的优化问题,我们可以将初始值设置为0,或者设置为随机数,对于神经网络的训练,一般设置为随机数,这对算法的收敛至关重要[1]。
学习率的设定
学习率设置为多少,也是实现时需要考虑的问题。最简单的,我们可以将学习率设置为一个很小的正数,如0.001。另外,可以采用更复杂的策略,在迭代的过程中动态的调整学习率的值。比如前1万次迭代为0.001,接下来1万次迭代时设置为0.0001。
面临的问题
在实现时,梯度下降法可能会遇到一些问题,典型的是局部极小值和鞍点问题,下面分别进行介绍。
局部极小值
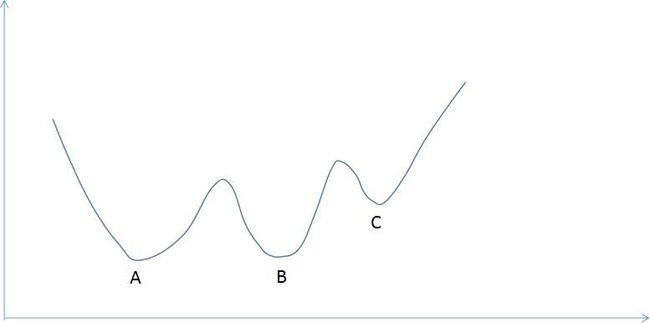
有些函数可能有多个局部极小值点,下面是一个例子:
这张图中的函数有3个局部极值点,分别是A,B和C,但只有A才是全局极小值,梯度下降法可能迭代到B或者C点处就终止。
鞍点
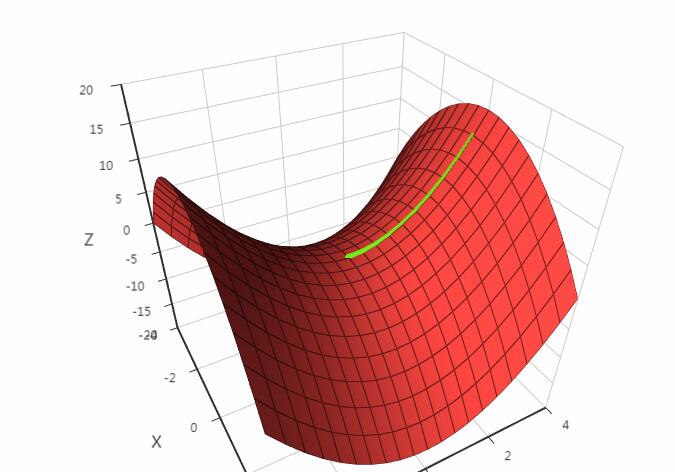
鞍点是指梯度为0,Hessian矩阵既不是正定也不是负定,即不定的点。下面是鞍点的一个例子,假设有函数:
显然在(0, 0)这点处不是极值点,但梯度为0,下面是梯度下降法的运行结果:
在这里,梯度下降法遇到了鞍点,认为已经找到了极值点,从而终止迭代过程,而这根本不是极值点。
对于怎么逃离局部极小值点和鞍点,有一些解决方案,在这里我们暂时不细讲,以后有机会再专门写文章介绍。对于凸优化问题,不会遇到上面的局部极小值与鞍点问题,即梯度下降法一定能找到全局最优解。凸优化的概念将在SIGAI后续的文章中介绍。
变种
梯度下降法有大量的变种,它们都只利用之前迭代时的梯度信息来构造每次的更新值,下面我们分别进行介绍。最直接的改进是为迭代公式加上动量项,动量项累积了之前的权重更新值,加上此项之后的参数更新公式为:
其中
动量项累积了之前的梯度信息,类似于保持行走时的惯性,以避免来回震荡,加快收敛速度。
AdaGrad的为自适应梯度,即adaptive gradient算法[2],是梯度下降法最直接的改进。唯一不同的是,AdaGrad根据前几轮迭代时的历史梯度值来调整学习率,参数更新公式为:
其中
AdaDelta算法[3]也是梯度下降法的变种,在每次迭代时也利用梯度值构造参数的更新值。假设要优化的参数为x,梯度下降法第t次迭代时计算出来的参数梯度值为
其中
在这里
这也是一个向量,计算时分别对向量的每个分量进行。然后计算参数的更新值:
参数更新的迭代公式为:
和带动量项的梯度下降法不同的是这里用历史梯度值来构造学习率,包括了梯度的平方值。
Adam算法[4]全称为adaptive moment estimation,它由梯度项构造了两个向量m和v,它们的初始值为0,更新公式为:
其中
在这里,用m代替梯度,用v来构造学习率。
NAG算法是一种凸优化方法,由Nesterov提出。和标准梯度下降法的权重更新公式类似,NAG算法构造一个向量v,初始值为0。v的更新公式为:
参数的更新公式为:
与带动量项的SGD相比NAG只是计算梯度时用的参数值不同,NAG计算误差梯度时考虑了动量项,使用的是
RMSProp算法[5]也是标准梯度下降法的变种,它由梯度值构造一个向量MS,初始化为0,更新公式为:
参数更新公式为:
其中
随机梯度下降法
对于有些机器学习问题,我们的目标函数是对样本的损失函数。假设训练样本集有N个样本,训练时优化的目标是这个数据集上的平均损失函数:
其中
批量随机梯度下降法在每次迭代中使用上面目标函数的随机逼近值,即只使用
个样本来近似计算损失函数。在每次迭代时要优化的目标函数变为:
已经证明,随机梯度下降法在数学期望的意义下收敛,即随机采样产生的梯度的期望值是真实的梯度。因为每次迭代时的目标函数实际上是不一样的,因此随机梯度下降法并不能保证每次迭代时函数值一定下降。
参考文献
[1] I. Sutskever, J. Martens, G. Dahl, and G. Hinton. On the Importance of Initialization and Momentum in Deep Learning. Proceedings of the 30th International Conference on Machine Learning, 2013.
[2] Duchi, E. Hazan, and Y. Singer. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. The Journal of Machine Learning Research, 2011.
[3] M. Zeiler. ADADELTA: An Adaptive Learning Rate Method. arXiv preprint, 2012.
[4] D. Kingma, J. Ba. Adam: A Method for Stochastic Optimization. International Conference for Learning Representations, 2015.
[5] T. Tieleman, and G. Hinton. RMSProp: Divide the gradient by a running average of its recent magnitude. COURSERA: Neural Networks for Machine Learning.Technical report, 2012.
[6] Rumelhart, David E.; Hinton, Geoffrey E.; Williams, Ronald J. (8 October 1986). Learning representations by back-propagating errors. Nature. 323 (6088): 533–536.
[7] L. Bottou. Stochastic Gradient Descent Tricks. Neural Networks: Tricks of the Trade. Springer, 2012.
推荐阅读:
[1] 机器学习-波澜壮阔40年 SIGAI 2018.4.13.
[2] 学好机器学习需要哪些数学知识?SIGAI 2018.4.17.
[3] 人脸识别算法演化史 SIGAI 2018.4.20.
[4] 基于深度学习的目标检测算法综述 SIGAI 2018.4.24.
[5] 卷积神经网络为什么能够称霸计算机视觉领域? SIGAI 2018.4.26.
[6] 用一张图理解SVM的脉络 SIGAI 2018.4.28.
[7] 人脸检测算法综述 SIGAI 2018.5.3.
[8] 理解神经网络的激活函数 SIGAI 2018.5.5.
[9]深度卷积神经网络演化历史及结构改进脉络-40页长文全面解读 SIGAI 2018.5.8.
原创声明
更多干货请关注V X公众号:SIGAI