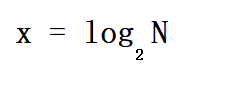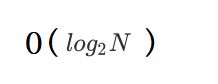不会有人还不知道这些常见代码的时间复杂度吧
☕目录☕
前言
常见代码的时间复杂度(一)
常见代码的时间复杂度(二)
常见代码的时间复杂度(三)
常见代码的时间复杂度(四)
常见代码的时间复杂度(五)
常见代码的时间复杂度(六)
常见代码的时间复杂度(七)
常见代码的时间复杂度(八)
写在最后
前言
本篇博客,只在列举一些常见的代码的时间复杂度的计算,作为这一篇博客的补充,有兴趣的可以来看一看:
【Java数据结构系列】第二章 —— 时间复杂度和空间复杂度
常见代码的时间复杂度(一)
public class TestDemo1 {
void func1 (int N){
int count = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
count++;
}
}
for (int k = 0; k < 2*N; k++) {
count++;
}
int M = 10;
while ((M--)>0){
count++;
}
}
}在func1中,我们可以看见,
有两个for循环嵌套,代码执行了 N^2 次,
下面一个for循环,代码执行了 2*N 次,
最后一个while循环,代码执行了 10 次,
所以func1执行的次数:F(N) = N^2 + 2*N + 10,
如果用 大O的渐进表示法表示,即:O(N^2)
常见代码的时间复杂度(二)
public class TestDemo2 {
void func2(int N) {
int count = 0;
for (int i = 0; i < 2*N; i++) {
count++;
}
int M=10;
while ((M--)>0){
count++;
}
System.out.println(count);
}
}很明显,在func2中,
for循环,代码执行了 2*N 次,
while循环,代码执行了 10 次,
即:func2中代码执行的次数:F(N) = 2*N + 10,
如果用 大O的渐进表示法表示,即:O(N)
常见代码的时间复杂度(三)
public class TestDemo3 {
void func3(int N,int M) {
int count = 0;
for (int i = 0; i < M; i++) {
count++;
}
for (int j = 0; j < N; j++) {
count++;
}
System.out.println(count);
}
}
在func3中,我们可以看见,
第一个for循环中,代码执行了 M 次,
第二个for循环中,代码执行了 N 次,
所以,在整个func3中,代码一共执行的次数:F(N) = M + N,
如果用 大O的渐进表示法表示,即:O(M+N)
常见代码的时间复杂度(四)
public class TestDemo4 {
void func4(int N) {
int count = 0;
for (int i = 0; i < 100; i++) {
count++;
}
System.out.println(count);
}
}
在func4中,我们可以看见,
for循环中,代码一共执行的次数:F(N) = 100,
如果用 大O的渐进表示法表示,即:O(1)
常见代码的时间复杂度(五)
public class TestDemo5 {
public static void bubbleSort(int[] array){
for (int i = 0; i < array.length-1; i++) {
boolean flg = false;
for (int j = 0; j < array.length-1-i; j++) {
if (array[j] > array[j+1]){
int tmp = array[j];
array[j] = array[j+1];
array[j+1] = tmp;
flg = true;
}
}
if (flg == false){
break;
}
}
}
}由上图我们可以看出,bubbleSort是一个升序的冒泡排序的算法,
假设,数组的长度就是N,即:array.length=N;
最好的情况下:正好所给的数据是 升序的数据(如:1,2,3,4,5,6,......,N)
此时,第一个for循环 i=0 时,执行到第二个for循环 j=array.length-1-i 后,
由于数组中的数据已经是 升序了,那么第二个for循环里面的if语句一直没有去执行,
即:flg一直是false,
那么,当执行下一句语句时,会执行break语句,直接跳出了循环,
即:第一个for循环只执行了一次,
即:在最好的情况下,程序一共执行的次数:F(N) = N,
也就是说,用大O的渐进法表示:O(N)
最坏的情况下:所给的数据 恰好是逆序的数据(如:N,N-1,N-2,......,3,2,1)
那么,很明显,两个for循环都要循环完,
即:冒泡N趟,
第一趟冒泡循环N次,
第二趟冒泡循环N-1次,
......
第N趟冒泡循环1次,
等差数列求和,准确次数(N+1)*N/2,
即:用大O的渐进法表示:O(N^2)
常见代码的时间复杂度(六)
public class TestDemo6 {
public static int Binary(int[] arr,int key){
int left=0;
int right=arr.length-1;
while(left<=right){
int mid=(left+right)/2;
if(keyarr[mid]){
left=mid+1;
}else{
return mid;
}
}
return -1;
}
} 很明显的,上面的代码是一个 二分查找的代码,
假设数组的长度是N,该程序一共执行了x次,
我们需要明白二分查找的思想,
一开始会给你一个数组,长度为N;
每查找一次,数组的长度都会减少到一半,
由于我们是按照最坏的情况 来计算时间复杂度的,那么,假设索要查找的数据就是最后一次所查找的,即 查找了x次以后,查找到了最后一个数据;
所以,我们就可以根据这个思想来计算出所要查找的次数x,
即:N/(2^x) = 1,
最后得出x的值:
常见代码的时间复杂度(七)
long factorial(int N) {
return N < 2 ? factorial(N-1) * N;
}在这里我们要知道,
递归的时间复杂度 = 递归的次数 * 每次递归之后 执行的次数;
在上面的递归中,每次递归之后 执行的次数 = 1,
即:此时 递归的时间复杂度 = 递归的次数;
而:由 factorial(N) —> factorial(N-1) —> factorial(N-2) —> ...... —> factorial(1),
递归次数一共是N次,
有的人可能会说,是从 factorial(N-1)开始的,
那也无所谓,时间复杂度反应的是一个大致的数据,
它们的时间复杂度都是:O(N)
常见代码的时间复杂度(八)
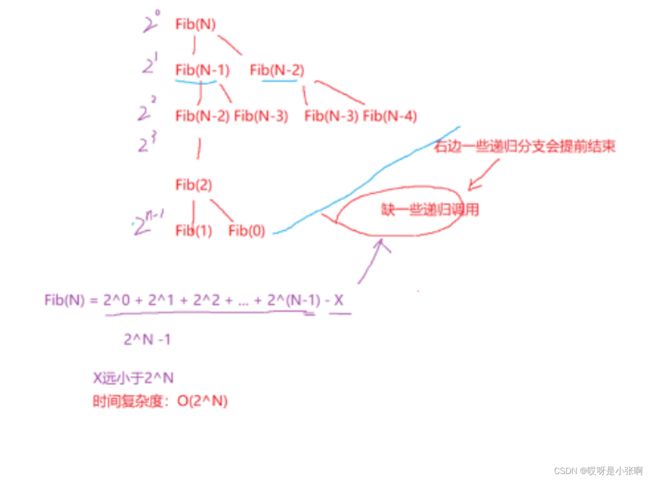
int Fib(int N) {
return N < 2 ? Fib(N-1) + Fib(N-2);
}时间复杂度为:O(2^N)
写在最后
由于博主水平有限,可能会出现一些表达不清楚,或者出现一些其他的情况,
欢迎各位铁汁们指出来,和博主一起改正,
一起努力,共同进步;
好了,如果这篇博客对铁汁们有帮助的话,可以送一个免费的 赞 嘛;
当然,顺手点个关注是再好不过的了......