dropout层_【深度学习理论】一文搞透Dropout、L1L2正则化/权重衰减

前言

本文主要内容——一文搞透深度学习中的正则化概念，常用正则化方法介绍，重点介绍Dropout的概念和代码实现、L1-norm/L2-norm的概念、L1/L2正则化的概念和代码实现～

要是文章看完还不明白，欢迎交流、分享、拍砖：）

详细内容如下：

• 1.正则化Regularization
  • 1.1 过拟合Overfitting
  • 1.2 欠拟合Underfitting
  • 1.3 泛化能力generalization ability
  • 1.4 解决或改善？
• 2.L1 L2正则化/权重衰减
  • 2.1 范数和欧几里得空间
    • 范数Norm
    • 欧几里得空间
  • 2.2 L1-范数和L2-范数
    • L1-范数
    • L2-范数
  • 2.3 L1/L2正则化和权重衰减
    • L1/L2正则化
    • 权重衰减weight decay
    • 代码实现—pytorch
• 3.Dropout
  • 3.1概述
    • 提出
    • 应用
    • 发展
  • 3.2 Vanilla Dropout
  • 3.3 Inverted Dropout
  • 3.4 代码实现——pytorch
    • 从零开始实现
    • 简洁实现
• 参考

原文发表于语雀文档：

【深度学习理论+代码】一文搞透Dropout、L1L2正则化/权重衰减 · 语雀​www.yuque.com

---

1.正则化Regularization

什么是正则化？其作用是怎样的？了解正则化之前，我们需要先了解一下机器学习中欠拟合和过拟合的概念

1.1 过拟合Overfitting

过度拟合的意思，意味着模型训练过程中，对训练集的模拟和学习过度贴合；
过拟合带来的影响：模型训练时的检测率很高效果很好，但是用于实际检验时，效果很差，模型不能很准确地预测，即泛化能力差。

1.2 欠拟合Underfitting

和过拟合相对，欠拟合是指模型和数据集间的拟合程度不够，学习不足。
欠拟合的影响：和过拟合相对，欠拟合是指模型和数据集间的拟合程度不够，可能是学习轮数不够、数据集特征不规则、模型选择有问题等。欠拟合时，模型的泛化能力同样会很差。

1.3 泛化能力generalization ability

是指一个机器学习算法对于没有见过的样本的识别能力。泛化能力自然是越高越好。
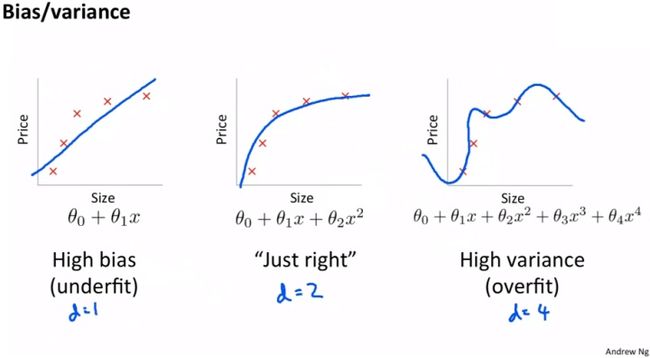
在吴恩达机器学习中有一个线性回归预测房价的例子，非常形象直观：

如上图，x轴表示房子面积，y轴表示房屋售价，图表中有5个样本点(训练集)，任务是找到合适的模型来拟合样本且用来预测未知的样本。
第一个模型是线性模型，对训练集样本欠拟合；
中间的二次方模型对样本拟合程度比较适中；
第三个四次方模型，对样本拟合程度更高，不过对于未来的新样本可能预测能力会很差，此为典型的过拟合。

1.4 解决或改善？

那么解决过拟合的方式有哪些？课程中给出了以下两点建议：1.丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征，或者使用一些模型选择的算法来帮忙（例如 PCA）2.正则化。保留所有的特征，但是减少参数的大小（magnitude）。当然，以上是机器学习中的一些通用做法，在深度学习中同样适用于。譬如深度学习中常见的降低过拟合/正则化方法：

• 使用L1正则化降低权重；
• 使用L2正则化/权重衰减weight decay；
• Early stopping 早停，防止过拟合；
• 使用BN层batch normalization来规范数据分布，间接起到正则化的作用；
• 使用Dropout(及各种变种和改进版)随机丢弃一些神经元，来减低模型对部分神经元的依赖，加强模型的鲁棒性，达到正则化的效果；
• Data augmentation数据增强，譬如将数据集图片处理后，增加平移旋转和缩放处理，增加噪声处理等，使得模型对各种复杂条件下的图像都能较好适应，增强鲁棒性。

有时L2正则化和weight decay常被人理解为同一种意思，实际上二者有时不可等价，见： https:// zhuanlan.zhihu.com/p/40 814046

当然，这么多正则化方式，每一点拎出来都可以出好几篇论文了～本文主要介绍的是常用的L2正则/权重衰减和Dropout，BN等放在以后的文章中介绍。

2.L1 L2正则化/权重衰减

本小节，讲讲L1正则化L2正则化和权重衰减(weight decay)，重点分为三个部分：

• 1.讲解L1/L2范数和L1/L2正则化的概念、来源、其在深度学习中的应用；
• 2.L2正则化和权重衰减的概念；
• 3.L2正则化/权重衰减在深度学习pytorch代码中的实现。

2.1 范数和欧几里得空间

范数Norm

在了解L1/L2正则化前，必须先了解L1-norm(L1范数)和L2-norm（L2范数），因为本质上，L1/L2正则化，即在机器学习/深度学习的loss损失函数中添加L1/L2范数的正则化项，以起到惩罚权重，达到正则化的效果，故称为L1/L2正则化。范数norm的定义是基于向量空间（Vector space）的，向量空间也称为线性空间，其概念起源于17世纪的解析几何、矩阵和欧几里得空间(Euclidean space)。我这里就不摆公式定义了，可以参考ｗｉｋｉ。

欧几里得空间

简单理解，欧几里得空间（Euclidean space）是向量空间的子集，起源于是古希腊学者欧几里得对物理空间的一种抽象(来源于生活中常见的二维平面，三维空间)并在其中定义了点线、内积、距离、角的概念。譬如：二维平面中一个点可以有坐标x,y；两点之间的距离表现为一条直线，其大小可以用

)表示；三维空间中，两点之间距离表现为一个向量，其大小可以用：

表示，两向量ａ和ｂ的内积定义为：

。当然，欧式空间也可以拓展至ｎ维度。在n=时，一个点需要用3个坐标来定义，而ｎ维欧式空间中，需要用n个坐标定义。

2.2 L1-范数和L2-范数

明明讨论的是范数，怎么扯到欧几里得空间去了？！

我也很无奈啊，因为Ｌ２范数也被称为欧几里得范数：）这里，我就不摆范数的定义了。简单来说，我们可以把L2-norm放在欧式空间中来理解，且直观地理解其意义为向量的模长。p-范数的公式定义如下：

L1-范数

p = 1时为L1范数(L1-norm):

L1范数(又称为Taxicab norm or Manhattan norm)，看起来L1-norm即一组数的绝对值累加和。

L2-范数

p = 2时为L2范数(L2-norm):

L2范数又称为欧几里得范数/平方范数(还可称为 L norm, ℓ norm, 2-norm)，其用于表示向量_ x = (_x, x, ..., x__n)距离原点的距离。

2.3 L1/L2正则化和权重衰减

L1/L2正则化

前面说了那么多，有木有一脸懵逼？？？别慌，都是浮云～我们只要记住L1范数是绝对值和，L2范数是平方和(开根号)即可。简单来说，L1/L2正则化就是在机器学习/深度学习中应用了L1/L2范数，具体来说，就是在损失函数loss上增加了L1或L2范数项，达到参数惩罚的作用，即实现了正则化的效果，从而称为L1/L2正则化。

在之前的专栏文章：【吴恩达机器学习】第三周—逻辑回归、过拟合、正则化中，有个栗子比较形象地展示了L2正则化的过程，如下图：

图中最右边的线性回归模型表达式为：

由于其高次项参数的使用，使得模型对训练数据过分拟合，导致对未来更一般的数据预测性大大下降，为了缓解这种过拟合的现象，我们可以采用L2正则化。具体来说就是在原有的损失函数上添加L2正则化项(l2-norm的平方)：

=>

这里，通过设置正则化系数

可以较好地惩罚高次项的特征，从而起到降低过拟合，正则化的效果。至于高次项的特征如何受到系数的影响，如何被惩罚的，详见：【吴恩达机器学习】第三周—逻辑回归、过拟合、正则化。添加L2正则化修正以后的模型曲线：

权重衰减weight decay

权重衰减weight decay，并不是一个规范的定义，而只是俗称而已，可以理解为削减/惩罚权重。在大多数情况下weight dacay 可以等价为L2正则化。L2正则化的作用就在于削减权重，降低模型过拟合，其行为即直接导致每轮迭代过程中的权重weight参数被削减/惩罚了一部分，故也称为权重衰减weight decay。从这个角度看，不论你用L1正则化还是L2正则化，亦或是其他的正则化方法，只要是削减了权重，那都可以称为weight dacay。
设：

• 参数矩阵为p（包括weight和bias）；
• 模型训练迭代过程中计算出的loss对参数梯度为d_p；
• 学习率lr；
• 权重衰减参数为decay

则不设dacay时，迭代时参数的更新过程可以表示为：p= p - lr×d_p;
增加weight_dacay参数后表示为：p = p - lr ×(d_p + p × dacay)

代码实现—pytorch

在深度学习框架的实现中，可以通过设置weight_decay参数，直接对weight矩阵中的数值进行削减（而不是像L2正则一样，通过修改loss函数）起到正则化的参数惩罚作用。二者通过不同方式，同样起到了对权重参数削减/惩罚的作用，实际上在通常的随机梯度下降算法(SGD)中，通过数学计算L2正则化完全可以等价于直接权重衰减。（少数情况除外，譬如使用Adam优化器时，可以参考：L2正则=Weight Decay？并不是这样）
正因如此，深度学习框架通常实现weight dacay/L2正则化的方式很简单，直接指定weight_dacay参数即可。

在pytorch/tensorflow等框架中，我们可以方便地指定weight_dacay参数，来达到正则化的效果，譬如在pytorch的sgd优化器中，直接指定weight_decay = 0.0001：

optimizer 

在模型训练过程中，每一轮迭代时通过：l.backward()来自动求梯度；之后通过optimizer.step()进行参数矩阵的梯度更新。

在sgd的代码实现中，我们重点看step()方法的第26行：if weight_decay != 0: 表示了应用weight_decay参数的情况；倒数第二行：p.add_(d_p, alpha=-group['lr'])表示了参数矩阵的梯度更新。

@torch.no_grad

---

3.Dropout

3.1概述

提出

Dropout的提出，源于2012年Hinton的一篇论文——《Improving neural networks by preventing co-adaptation of feature detectors》。论文中描述了当数据集较小时而神经网络模型较大较复杂时，训练时容易产生过拟合，为了防止过拟合，可以通过阻止特征检测器间的共同作用来提高模型性能。

应用

2012年，大名鼎鼎的AlexNet网络的论文——《ImageNet Classification with Deep Convolutional Neural Networks》中，应用了Dropout,并且证明了其在提高模型精度和降低过拟合方面效果出色。由于AlexNet有效的网络结构+Dropout的应用，此模型在12年的ImageNet分类赛上以大幅优势领先第二名，从而使得深度卷积神经网络CNN在图像分类上的应用掀起一波热潮～

发展

在这以后，围绕Dropout又涌现出不少论文：
《Dropout:A Simple Way to Prevent Neural Networks from Overfitting》
《Improving Neural Networks with Dropout》
《Dropout as data augmentation》
等等。

不过总结起来，Dropout的原理都类似，只是实现方式有不同而已。比较流行的实现主要有两种类型：

• Vanilla Dropout
• Inverted Dropout

其中Vanilla Dropout是原论文中提出的，朴素实现版本；而Inverted Dropout则是更广为使用和流行的实现

3.2 Vanilla Dropout

Vanilla Dropout是原论文中提出的，这里我简单介绍下主要原理和流程。从上面的介绍中可知，Dropout的提出是为了降低过拟合的，具体是应用在深度神经网络的中间隐藏层上，对于某一层l,如果应用了概率p（可选超参数，例如可设置p = 0.5）的Dropout,即表面该层的神经元，在网络的训练/测试过程中，每个神经元都有50%的概率被“丢弃”，即此神经元不参与权重矩阵的计算。
具体流程如下：

模型训练时应用Dropout的流程，概况一下描述就是：

• 1.随机概率p随机dropout部分神经元，并前向传播
• 2.计算前向传播的损失，应用反向传播和梯度更新(对剩余的未被dropout的神经元)
• 3.恢复所有神经元的，并重复过程1

此训练过程理解起来很简单，但是有个问题，就是测试时会比较麻烦。为了保持模型的分布相同，测试时也需要保持模型分布和训练时一样，需要以一个概率p来丢失部分神经元(即乘以1-p的概率来保留),这样会不太方便，而且同一个输入可能每次预测的结果不一样，不稳定。所以Vanilla Dropout并没有得到广泛应用，取而代之的是更方便的Inverted Dropout,我们在之前的文章——【吴恩达深度学习】—参数、超参数、正则化中介绍的就是这种Dropout。

3.3 Inverted Dropout

Inverted Dropout是在在各大深度学习框架中是更广泛使用的版本，其原理类似，就是实现起来和原始版本的dropout稍微有些区别。Inverted Dropout在训练阶段,同样应用p的概率来随机失活，不过额外提前除以1-p，这样相当于将网络的分布提前“拉伸”了，好处就是在预测阶段，网络无需再乘以1-p(来压缩分布)，这样预测时网络无需改动，输出也更加稳定。丢弃法不改变输入的期望
假设随机变量

为0和1的概率分别为p和1-p(丢弃和保留的概率)，则任意神经元

可以表示为：

而

，所以有：

即，Dropout并不改变神经元的期望值，即不改变整个输入的期望。

3.4 代码实现——pytorch

下面，我们借用《动手学习深度学习-pytorch版》的一个例子来描述Inverted Dropout的原理和代码实现。

首先，我们的神经网络模型如下：

很简单总共3层，输入层4个神经元；中间隐藏层5个神经元

；输出层3个；

ϕ_为激活函数，输入为

，隐藏层中单元i的权重参数为：

，偏差bias为bi

则隐藏层激活单元表达式如下：

对隐藏层使用Dropout，设隐藏层中任意神经元被“丢弃” 的概率设为p，（保留的概率为1-p）。所谓的丢弃指将此神经元的值设为0(故其值不能被传递到下一层，相当于被砍掉了)。使用Dropout后，可能的一种网络形态：

代码实现主要是这个简单神经网络模型在Fashion-mnist数据集上的训练，部分和书中一样，有两种实现方式：

• 1.从零开始实现
• 2.简洁版实现

1.从零开始实现主要是自定义dropout函数，自定义网络等；2.简洁实现即用pytorch现成的dropout和网络定义来实现模型的训练。

从零开始实现

为了表达对于某一层输入X应用dropout,我们可以定义以下函数：

def 

dropout函数核心有两点：

• 1.mask = (torch.rand(X.shape) < keep_prob).float()
• 2. Y = mask * X / keep_prob

1.mask矩阵使用torch.rand可以产生0~1之间均匀分布的数字，< keep_prob(=1-p)处理后得到的矩阵中元素为True的概率为1-p,为False的概率为p，float()转换为1和0后，即完成了dropout的过程。mask矩阵和X相乘来模拟随机dropout(×0.0的即被失活，×1.0的即得到保留)2.mask * X即完成了p概率的dropout,再除以1-p是为了后面预测阶段无需更改网络
完整代码如下：

import 

简洁实现

import 

参考

• 深度学习中Dropout原理解析
• 神经网络Dropout层中为什么dropout后还需要进行rescale？
• 都9102年了，别再用Adam + L2 regularization了
• l1正则与l2正则的特点是什么，各有什么优势？
• 《动手学习深度学习》-pytorch版
• https://en.wikipedia.org/wiki/Norm_(mathematics)