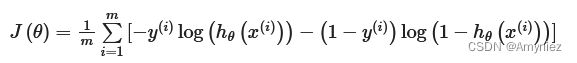逻辑回归（Logistics Regression）

1. 前言

    今天学习了吴恩达机器学习的逻辑回归部分，逻辑回归属于分类问题（classification），这里主要是考虑有sigmoid函数（也叫做Logistic函数）。
    这里我主要是介绍一些逻辑回归函数的实现过程。首先，我的数据来源于吴恩达机器学习数据集（学生录取成绩数据，含标签label（0,1））。设想你是大学相关部分的管理者，想通过申请学生两次测试的评分，来决定他们是否被录取。现在你拥有之前申请学生的可以用于训练逻辑回归的训练样本集。对于每一个训练样本，你有他们两次测试的评分和最后是被录取的结果，通过逻辑回归的方式来对其他学生的成绩进行预测。

2. 实现过程

2.1 数据可视化过程

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

path = r'C:\Users\Administrator\Desktop\logisticRegression_1.txt' # 对样本1进行训练
data = pd.read_csv(path, header=None, names=['Exam 1', 'Exam 2', 'Admitted'])
data.head()

positive = data[data['Admitted'].isin([1])] # .isin是pandas中DataFrame的布尔索引，可以用满足布尔条件的列值来‘过滤数据’
negative = data[data['Admitted'].isin([0])]

fig, ax = plt.subplots(figsize=(8,5)) # 产生空白画布，设置画布大小
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=50, c='b', marker='o', label='Admitted') # 列表；s：size；蓝色；
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=50, c='r', marker='x', label='Not Admitted') #红色
ax.legend() # legend n.（图片或地图的）文字说明，图例
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
plt.show()

2.2 Sigmoid函数

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

nums = np.arange(-10, 10, step=1)

# plt.subplots()创建一个画像(figure)和一组子图(subplots)；
# 返回一个Figure实例fig和一个AcesSubplot实例ax；
# flg代表整个图像，ax代表坐标轴和画的图。
fig, ax = plt.subplots(figsize=(8,5))
ax.plot(nums, sigmoid(nums), 'r')
plt.show()

2.3 代价函数（costFunction）

# costFunction定义
def cost(theta, X, y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
    return np.sum(first - second) / (len(X))

2.4 其他设置

# 添加1列数据x0
data.insert(0, 'Ones', 1)

# 设置X和y数据
cols = data.shape[1]         # 1表示列，矩阵的第二维
X = data.iloc[:,0:cols-1]
y = data.iloc[:,cols-1:cols] # 取出最后一列数据

# 将数值转换为数组格式，并初始化theta值
X = np.array(X.values)
y = np.array(y.values)
theta = np.zeros(3)

代价计算：

cost(theta, X, y)

0.6931471805599453（效果不错）

2.5 梯度下降函数

注意：我们实际上没有在这个函数中执行梯度下降，我们仅仅在计算一个梯度步长。这是一个优化的过程，就像Octave中的 fminunc() 函数一样，寻找最优的成本和梯度参数。而在Python中，可以用SciPy的 optimize 命名空间来做同样的事情。

def gradient(theta, X, y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    
    parameters = int(theta.ravel().shape[1])
    grad = np.zeros(parameters)
    
    error = sigmoid(X * theta.T) - y
    
    for i in range(parameters):
        term = np.multiply(error, X[:,i])
        grad[i] = np.sum(term) / len(X)
    
    return grad

此处的代码，我还没有完全弄明白，还需要继续学习相关的优化算法，之后再回过头来思考！！！

2.5.1 梯度下降结果（初始参数为0）：

gradient(theta, X, y)

array([ -0.1 , -12.00921659, -11.26284221])

2.5.2 SciPy’s truncated newton（TNC）寻找最优参数：

import scipy.optimize as opt
result = opt.fmin_tnc(func=cost, x0=theta, fprime=gradient, args=(X, y))
result

(array([-25.16131863, 0.20623159, 0.20147149]), 36, 0)

2.5.3 代价计算：

cost(result[0], X, y)

0.20349770158947458（比之前计算的代价值更好，达到了优化算法的目的）

2.6 精度函数

def predict(theta, X):
    probability = sigmoid(X * theta.T)
    return [1 if x >= 0.5 else 0 for x in probability]

theta_min = np.matrix(result[0])
predictions = predict(theta_min, X)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]
accuracy = (sum(map(int, correct)) % len(correct))
print ('accuracy = {0}%'.format(accuracy))

accuracy = 89%(效果不错，但是可能会高于真实值)

3. 逻辑回归实现

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import math

# OrderedDict实现了对字典对象中元素的排序；
# 普通的字典，传入的顺序不一样，但是依然是相同的字典（输出一样）；
# orderedDict字典，传入的顺序不一样，那么得到的字典是不一样的（按照输入的顺序进行排列）。
from collections import OrderedDict 


# 1.数据导入
def inputData():
    data = pd.read_csv('C:\\Users\\Administrator\\Desktop\\logisticRegression_1.txt'
                ,dtype={0:float,1:float,2:int}) 
    data.insert(0,"one",[1 for i in range(0,data.shape[0])]) #插入全为1的列，即theta0用于矩阵线性计算
    # 读取X和y
    # iloc（）：前面的冒号是取行数，后面的冒号是取列数，
    X=data.iloc[:,0:3].values  # 取.txt文件取每行的前 3 列
    y=data.iloc[:,3].values    # 取.txt文件的第 3 列
    y=y.reshape(y.shape[0],1)  # shape（）：查看数据有多少行多少列，0表示行数，1表示列数
                               # reshape()：数组array中的方法，将数据重构
    return X,y


# 2.数据可视化
def showData(X,y):
    for i in range(0, X.shape[0]):  # range(start, stop, step)；开始值默认为0；左闭右开；
        if(y[i,0]==1):
            plt.scatter(X[i,1],X[i,2],marker='o', s=50, c='b',label='Admitted')
        elif(y[i,0]==0):
            plt.scatter(X[i,1],X[i,2],marker='x', s=50, c='r',label='Not admitted')
    #设置坐标轴和图例
    plt.xticks(np.arange(30,110,10)) # 步长为10
    plt.yticks(np.arange(30,110,10))
    plt.xlabel('Exam 1 score')
    plt.ylabel('Exam 2 score')
    #因为上面绘制的散点不做处理的话，会有很多重复标签
    #因此这里导入一个集合类消除重复的标签
    handles, labels = plt.gca().get_legend_handles_labels()     # 获得标签,gca:Get Current Axes
    by_label = OrderedDict(zip(labels, handles))                # 通过集合来删除重复的标签
    plt.legend(by_label.values(), by_label.keys())              # 显示图例
    plt.show()

    
# 3.sigmoid函数
def sigmoid(z):
    return 1/(1+np.exp(-z))


# 4.代价函数
def showCostsJ(X,y,theta,m):
    # 式子中加了1e-6次方是为了扩大精度，防止出现除0的警告！！！
    # X @ theta与X.dot(theta)等价，X*theta
    costsJ = ((y*np.log(sigmoid(X@theta)+ 1e-6))+((1-y)*np.log(1-sigmoid(X@theta)+ 1e-6))).sum()/(-m)
    return costsJ


# 5.梯度下降函数
def gradientDescent(X,y,theta,m,alpha,iterations):
    for i in range(0,iterations): 
        ys=sigmoid(X@theta)-y
        temp0=theta[0][0]-alpha*(ys*(X[:,0].reshape(X.shape[0],1))).sum()  #注意这里一定要将X[:,1]reshape成向量
        temp1=theta[1][0]-alpha*(ys*(X[:,1].reshape(X.shape[0],1))).sum()
        temp2=theta[2][0]-alpha*(ys*(X[:,2].reshape(X.shape[0],1))).sum()
        theta[0][0]=temp0          #进行同步更新θ0和θ1和θ2
        theta[1][0]=temp1
        theta[2][0]=temp2

        # 使用X.T@ys可以替代掉之前的同步更新方式，更简洁
        # theta=theta-alpha*(X.T@ys)/m
        
    return theta


# 6.决策边界可视化函数
def evaluateLogisticRegression(X,y,theta):
    # 与数据可视化函数相同
    for i in range(0,X.shape[0]):
        if(y[i,0]==1):
            plt.scatter(X[i,1],X[i,2],marker='o', s=50, c='b',label='Admitted')
        elif(y[i,0]==0):
            plt.scatter(X[i,1],X[i,2],marker='x', s=50, c='r',label='Not admitted')
    plt.xticks(np.arange(30,110,10))
    plt.yticks(np.arange(30,110,10))
    plt.xlabel('Exam 1 score')
    plt.ylabel('Exam 2 score')
    handles, labels = plt.gca().get_legend_handles_labels()
    by_label = OrderedDict(zip(labels, handles))
    plt.legend(by_label.values(), by_label.keys())

    minX=np.min(X[:,1])         #取得x1中的最小值
    maxX=np.max(X[:,1])         #取得x1中的最大值
    xx=np.linspace(minX,maxX,100)   #创建等间距的数100个
    yy=(theta[0][0]+theta[1][0]*xx)/(-theta[2][0])      #绘制决策边界
    plt.plot(xx,yy)
    plt.show()

    
# 7.准确率函数
def judge(X,y,theta):
    ys=sigmoid(X@theta)         #根据假设函数计算预测值ys
    yanswer=y-ys                #使用真实值y-预测值ys
    yanswer=np.abs(yanswer)     #对yanswer取绝对值
    print('accuary:',(yanswer<0.5).sum()/y.shape[0]*100,'%')   #计算准确率并打印结果


X,y = inputData()           #输入数据   
theta=np.zeros((3,1))       #初始化theta数组
alpha=0.0002                 #设定alpha值
iterations=200000            #设定迭代次数
theta=gradientDescent(X,y,theta,X.shape[0],alpha,iterations)        #进行梯度下降
judge(X,y,theta)            #计算准确率
evaluateLogisticRegression(X,y,theta)  

accuary: 91.91919191919192 %

4. 正则化逻辑回归实现（减少过拟合，提高泛化能力）

当特征值features过多，且数据量少于特征值时，将会出现过拟合的情况，过拟合的泛化效果不好，不能应用于其他的预测项目中，所以需要进行调整，主要包括两种方法：

• 1.减少特征值的个数；
• 2.正则化（regularization）；

正则化就是保证特征数量不变的情况下，减小特征值的大小或者量级，即对特征值进行相应的惩罚，其中包括：lamda（正则参数 regularization parameter）。

图一表示欠拟合，图二是合适的分类结果，图三为过拟合的情况。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt

# 对样本2进行训练
# 数据读取
path = r'C:\Users\Administrator\Desktop\logisticRegression_2.txt' 
data2 = pd.read_csv(path, header=None, names=['Test 1', 'Test 2', 'Accepted'])
data2.head()

# 数据可视化
positive = data2[data2['Accepted'].isin([1])]
negative = data2[data2['Accepted'].isin([0])]

fig, ax = plt.subplots(figsize=(8,5))
ax.scatter(positive['Test 1'], positive['Test 2'], s=50, c='b', marker='o', label='Accepted')
ax.scatter(negative['Test 1'], negative['Test 2'], s=50, c='r', marker='x', label='Rejected')
ax.legend()
ax.set_xlabel('Test 1 Score')
ax.set_ylabel('Test 2 Score')
plt.show()

# 创建新的多项式特征theta，一共10个theta
degree = 5
x1 = data2['Test 1']
x2 = data2['Test 2']

data2.insert(3, 'Ones', 1)

for i in range(1, degree):
    for j in range(0, i):
        data2['F' + str(i) + str(j)] = np.power(x1, i-j) * np.power(x2, j)

data2.drop('Test 1', axis=1, inplace=True)
data2.drop('Test 2', axis=1, inplace=True)

data2.head()

4.1 正则化函数：

实行过程：

# 正则化代价函数
def costReg(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
    reg = (learningRate / (2 * len(X))) * np.sum(np.power(theta[:,1:theta.shape[1]], 2))
    return np.sum(first - second) / len(X) + reg

吴恩达老师讲到的正则化原理，其中分为两部分，theta0不需要进行正则化：

def gradientReg(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    
    parameters = int(theta.ravel().shape[1])
    grad = np.zeros(parameters)
    
    error = sigmoid(X * theta.T) - y
    
    for i in range(parameters):
        term = np.multiply(error, X[:,i])
        
        if (i == 0):
            grad[i] = np.sum(term) / len(X)
        else:
            grad[i] = (np.sum(term) / len(X)) + ((learningRate / len(X)) * theta[:,i])
    
    return grad

5. 正则化完整实现

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict

#用于导入数据的函数
def inputData():
    #从txt文件中导入数据，注意最好标明数据的类型
    data=pd.read_csv('C:\\Users\\Administrator\\Desktop\\logisticRegression_2.txt'
                ,dtype={0:float,1:float,2:int})
    #插入一列全为1的列
    data.insert(0,"ones",np.ones((data.shape[0],1)))
    #分别取出X和y
    X=data.iloc[:,0:3]
    X=X.values
    y=data.iloc[:,3]
    y=(y.values).reshape(y.shape[0],1)
    return X,y

#用于最开始进行数据可视化的函数
def showData(X,y):
    #分开考虑真实值y是1和0的行，分别绘制散点，并注意使用不同的label和marker
    for i in range(0,X.shape[0]):
        if(y[i][0]==1):
            plt.scatter(X[i,1],X[i,2],marker='o', s=50, c='b',label='y=1')
        else:
            plt.scatter(X[i,1],X[i,2],marker='x', s=50, c='r',label='y=0')
    #设置坐标轴和图例
    plt.xticks(np.arange(-1,1.5,0.5))
    plt.yticks(np.arange(-0.8,1.2,0.2))
    plt.xlabel('Microchip Test 1')
    plt.ylabel('Microchip Test 2')
    #因为上面绘制的散点不做处理的话，会有很多重复标签
    #因此这里导入一个集合类消除重复的标签
    handles, labels = plt.gca().get_legend_handles_labels()     #获得标签
    by_label = OrderedDict(zip(labels, handles))                #通过集合来删除重复的标签
    plt.legend(by_label.values(), by_label.keys())              #显示图例
    plt.show()

#定义sigmoid函数
def sigmoid(z):
    return 1/(1+np.exp(-z))

#计算代价值的函数
def computeCostsJ(X,y,theta,lamda,m):
    #根据吴恩达老师上课讲的公式进行书写
    hx=sigmoid(X@theta)
    costsJ=-(np.sum(y*np.log(hx)+(1-y)*np.log(1-hx)))/m+lamda*np.sum(np.power(theta,2))/(2*m)
    return costsJ

#进行特征映射
def featureMapping(x1,x2,level):
    answer = {}         #定义一个字典
    for i in range(1,level+1):      #外层循环，映射的阶数
        for j  in range(0,i+1):     #内存循环，x1的次数
            answer['F{}{}'.format(i-j,j)]=np.power(x1,i-j)*np.power(x2,j)    #形成字典中的key-value   
    answer = pd.DataFrame(answer)       #转换为一个dataframe
    answer.insert(0,"ones",np.ones((answer.shape[0],1)))        #插入第一列全1
    return answer.values

#进行梯度下降的函数
def gradientDescent(X,y,theta,alpha,iterations,m,lamda):
    for i in range(0,iterations+1):
        hx=sigmoid(X@theta)
        temp0=theta[0][0]-alpha*np.sum(hx-y)/m          #因为x0是不需要进行正则化的，因此需要单独计算
        theta=theta-alpha*(X.T@(hx-y)+lamda*theta)/m    #根据公式进行同步更新theta
        theta[0][0]=temp0                           #单独修改theta0
    return theta

#利用训练集数据判断准确率的函数
def judge(X,y,theta):
    ys=sigmoid(X@theta)         #根据假设函数计算预测值ys
    yanswer=y-ys                #使用真实值y-预测值ys
    yanswer=np.abs(yanswer)     #对yanswer取绝对值
    print('accuary',(yanswer<0.5).sum()/y.shape[0]*100,'%')    #计算准确率并打印结果

#对决策边界进行可视化的函数
def evaluateLogisticRegression(X,y,theta):
    #这里和上面进行数据可视化的函数步骤是一样的，就不重复阐述了
    for i in range(0,X.shape[0]):
        if(y[i][0]==1):
            plt.scatter(X[i,1],X[i,2],marker='o', s=50, c='b',label='y=1')
        else:
            plt.scatter(X[i,1],X[i,2],marker='x', s=50, c='r',label='y=0')
    plt.xticks(np.arange(-1,1.5,0.5))
    plt.yticks(np.arange(-0.8,1.2,0.2))
    plt.xlabel('Microchip Test 1')
    plt.ylabel('Microchip Test 2')
    handles, labels = plt.gca().get_legend_handles_labels()
    by_label = OrderedDict(zip(labels, handles))
    plt.legend(by_label.values(), by_label.keys())
    
    #通过绘制等高线图来绘制决策边界
    x=np.linspace(-1,1.5,250)       #创建一个从-1到1.5的等间距的数
    xx,yy = np.meshgrid(x,x)        #形成一个250*250的网格，xx和yy分别对应x值和y值
    #利用ravel()函数将xx和yy变成一个向量，也就是62500*1的向量
    answerMapping=featureMapping(xx.ravel(),yy.ravel(),6)   #进行特征映射
    answer=answerMapping@theta      #代入映射后的数据进行计算预测值
    answer=answer.reshape(xx.shape) #将answer换成一样格式
    plt.contour(xx,yy,answer,0)     #绘制等高线图，0代表绘制第一条等高线
    plt.show()


X,y = inputData()       #导入数据
theta=np.zeros((28,1))      #初始化theta数组
iterations=200000       #定义迭代次数
alpha=0.001             #定义alpha值
lamda=50             #定义lamda
mappingX = featureMapping(X[:,1],X[:,2],6)      #进行特征映射
theta=gradientDescent(mappingX,y,theta,alpha,iterations,X.shape[0],lamda)   #进行正则化的梯度下降
judge(mappingX,y,theta)         #计算预测的准确率
evaluateLogisticRegression(X,y,theta)       #绘制决策边界

accuary 65.8119658119658 %