直纹面的简要介绍 以及matlab程序实现

一. 直纹面的定义

        直纹面是一类特殊的曲面，它可以由一族直线“织成”，即过曲线上每一点都存在过该点的直线落在该曲面上。
        直纹面在几何造型中的应用非常广泛。直纹面是直线段在空间中沿某一定曲线运动所形成的轨迹. 定曲线称为准线，直线段称为母线。如下图：

        设准线为$h(u)$, 母线的方向向量为$l(u)$, 则直纹面的方程为：
       
$$P(u,v)=h(u)+vh(u),$$
其中，$u\in [u_0,u_1],v\in [v_0,v_1].$

       在实际应用中，直纹面还可以表示为
       
$$P(u,v)=(1-v)a(u)+vb(u),$$
其中，$u\in [u_0,u_1],v\in [0,1].$ 显然曲线$a(u),b(u)$为直纹面在$v=0,1$时的两条边界曲线
       
       

       
       
       

二. matlab程序：

function Ruled_surface
% 直纹面编程示例：
% 直纹面方程：p(u,v) = (1-u)*a(v) + u*b(v) ; 
% 其中a(v)，b(v)程序中分别取了两个bezier曲线
clear;
clc;
[U,V] = meshgrid(0:0.02:1,0:0.02:1);
%第一条bezier曲线  a(v)
rx=[0,1,2,3,4,7];
ry=[0,0,-3,5,6,6];                         %控制顶点(0,0),(1,0),(2,-3),...
M = 40;
hx = 1/M;                                    %将[0,1]区间M等分
x = V;
n=length(rx)-1;
Rx = 0;
Ry = 0;
for i = 1:n+1
    Rx = Rx + rx(i)*B(x,n,i-1) ;       %将控制顶点与Bernstein基函数相乘得到bezier曲线
    Ry = Ry + ry(i)*B(x,n,i-1) ;
end
figure(1)
plot(Rx,Ry,'r')                             %bezier曲线a(v)

%第二条bezier曲线  b(v)
px=[0,1,2,3,4,6];
py=[0,2,15,5,6,6];                       %控制顶点(0,0),(1,2),....
M = 40;
hx = 1/M;                                    %将[0,1]区间M等分
x = V;
n=length(px)-1;
PX = 0;
PY = 0;
for i = 1:n+1
    PX = PX + px(i)*B(x,n,i-1) ;       %将控制顶点与Bernstein基函数相乘得到bezier曲线
    PY = PY + py(i)*B(x,n,i-1) ;
end
figure(2)
plot(PX,PY,'b')                              %bezier曲线b(v)

%将两条边界bezier曲线带入直纹面方程
X = (1-U).*Rx + U.*PX;
Y = (1-U).*Ry + U.*PY ;
Z = (1-U).*2 + U.*(33) ;
%两种方式画图
figure(3)
surf(U,V,Y)
figure(5)
surf(X,Y,Z)
figure(4)
mesh(X,Y,Z)
end
%  第i个bernstein基函数
function y = B(x,n,i)
y = N(n,i).*(x.^i).*((1-x).^(n-i));
end
% 组合数  Number of combinations
function y = N(n,i)
y1 = factorial(n);            %n的阶乘
y2 = factorial(i)*factorial(n-i);
y = y1/y2;
end

可以直接在matlab上运行的。

              
       

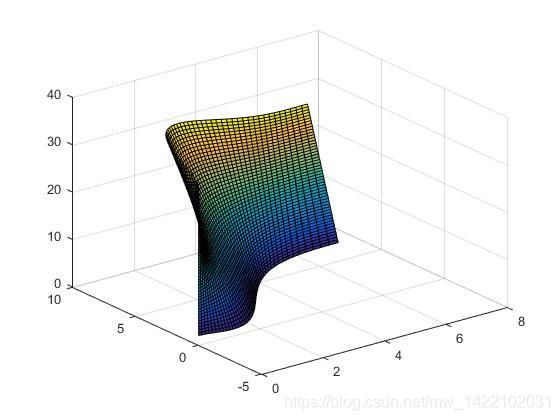
三. 图像

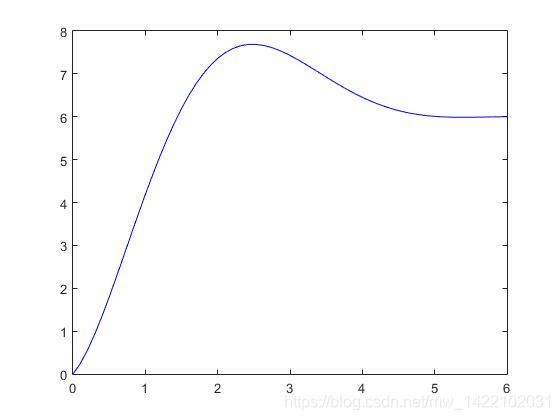
1.第一条边界bezier曲线：

      
        
2. 第二条边界bezier曲线：

       
3. 最终生成的直纹面

四、更新后的程序：

function Ruled_surface_1
% date : 2020.10.15
% 直纹面编程示例：
% 直纹面方程：p(u,v) = (1-u)*a(v) + u*b(v) ; 
% 其中a(v)，b(v)程序中分别取了两个bezier曲线
% author ： mw_1422102031
clear;
clc;
% 直纹面编程示例：
% 直纹面方程：p(u,v) = (1-u)*a(v) + u*b(v) ; 
% 其中A(v)，B(v)程序中分别取了两个bezier曲线

 %A曲线的控制顶点
A0 = [0,0,0];  A1 = [1,1,0];  A2 = [2,0,0]; 
ax = [A0(1),A1(1),A2(1)];
ay = [A0(2),A1(2),A2(2)];
az = [A0(3),A1(3),A2(3)];                                  
[U,V] = meshgrid(0:0.02:1,0:0.02:1);
%B曲线的控制顶点
B0 = [0.5,0,0.5];  B1 = [1,1,2];  B2 = [3,0,1];
bx = [B0(1),B1(1),B2(1)];
by = [B0(2),B1(2),B2(2)];
bz = [B0(3),B1(3),B2(3)];
%A_bezier曲线
x = V;
n=length(ax)-1;
Ax = 0;
Ay = 0;
Az = 0;
for i = 1:n+1
    Ax = Ax + ax(i)*B(x,n,i-1) ;       %将控制顶点与Bernstein基函数相乘得到bezier曲线
    Ay = Ay + ay(i)*B(x,n,i-1) ;
    Az = Az + az(i)*B(x,n,i-1) ;
end
figure(1)
plot3(ax,ay,az,'k',ax,ay,az,'m*')  
hold on
plot3(Ax,Ay,Az,'r')                             %bezier曲线a(v)

%B_bezier曲线
x = V;
n=length(bx)-1;
Bx = 0;  By = 0;  Bz = 0;
for i = 1:n+1
    Bx = Bx + bx(i)*B(x,n,i-1) ;       %将控制顶点与Bernstein基函数相乘得到bezier曲线
    By = By + by(i)*B(x,n,i-1) ;
    Bz = Bz + bz(i)*B(x,n,i-1) ;
end
figure(2)
plot3(bx,by,bz,'k',bx,by,bz,'m*')  
hold on
plot3(Bx,By,Bz,'r')   

%将两条边界bezier曲线带入直纹面方程
X = (1-U).*Ax + U.*Bx ;
Y = (1-U).*Ay + U.*By ;
Z = (1-U).*Az + U.*Bz ;
%两种方式画图
figure(3)
mesh(X,Y,Z)
figure(4)
mesh(X,Y,U)    %总感觉有点怪怪的
end

总感觉有问题，如果有人发现有什么问题给我说一下，谢谢！

% date : 2020.10.15
% 直纹面编程示例：
% 直纹面方程：p(u,v) = (1-u)*a(v) + u*b(v) ; 
% 其中a(v)，b(v)程序中分别取了两个bezier曲线
% author ： mw_1422102031
clear;
clc;
% 直纹面编程示例：
% 直纹面方程：p(u,v) = (1-u)*a(v) + u*b(v) ; 
% 其中A(v)，B(v)程序中分别取了两个bezier曲线

 %A曲线的控制顶点
% A0 = [0,0,0];  A1 = [1,1,0];  A2 = [2,0,0]; 
ax = [0,1,2,3,4,6];
ay = [0,2,15,5,6,6]; 
az = [0,1,0,1,0,0];                                   
[U,V] = meshgrid(0:0.02:1,0:0.02:1);
%B曲线的控制顶点
% B0 = [0.5,0,0.5];  B1 = [1,1,2];  B2 = [3,0,1];
bx = [2,1,2,3,4,7];
by = [1,0,-3,5,6,6];    
bz = [1,0,1,0,0,3];    
%A_bezier曲线
x = V;
n=length(ax)-1;
Ax = 0;
Ay = 0;
Az = 0;
for i = 1:n+1
    Ax = Ax + ax(i)*B(x,n,i-1) ;       %将控制顶点与Bernstein基函数相乘得到bezier曲线
    Ay = Ay + ay(i)*B(x,n,i-1) ;
    Az = Az + az(i)*B(x,n,i-1) ;
end
figure(1)
plot3(ax,ay,az,'k',ax,ay,az,'m*')  
hold on
plot3(Ax,Ay,Az,'r')                             %bezier曲线a(v)

%B_bezier曲线
x = V;
n=length(bx)-1;
Bx = 0;  By = 0;  Bz = 0;
for i = 1:n+1
    Bx = Bx + bx(i)*B(x,n,i-1) ;       %将控制顶点与Bernstein基函数相乘得到bezier曲线
    By = By + by(i)*B(x,n,i-1) ;
    Bz = Bz + bz(i)*B(x,n,i-1) ;
end
figure(2)
plot3(bx,by,bz,'k',bx,by,bz,'m*')  
hold on
plot3(Bx,By,Bz,'r')   

%将两条边界bezier曲线带入直纹面方程
X = (1-U).*Ax + U.*Bx ;
Y = (1-U).*Ay + U.*By ;
Z = (1-U).*Az + U.*Bz ;
%两种方式画图
figure(3)
mesh(X,Y,Z)
figure(4)
mesh(X,Y,U)

更新的程序用到的函数：

%  第i个bernstein基函数
function y = B(x,n,i)
y = N(n,i).*(x.^i).*((1-x).^(n-i));
end
% 组合数  Number of combinations
function y = N(n,i)
y1 = factorial(n);            %n的阶乘
y2 = factorial(i)*factorial(n-i);
y = y1/y2;
end