1. 分类与回归树原理(CART)
1. 简介
分类与回归树(Classification And Regression Tree),采用二分递归分割技术,将当前样本集划分成两个子集,即其结构为二叉树,每个内部节点均只有两个分支。左分支为特征值为True的样本集合,右分支为特征取值为False的样本集合。
CART既可以处理连续型特征,也可以处理离散型特征,基于预测值的取值类![]() 型不同,可划分成回归树和分类树两种。
型不同,可划分成回归树和分类树两种。
- 预测值为连续型变量,则CART生成回归树。
- 预测值为离散型变量,则CART生成分类树。
2. 特征处理
CART既可以使用离散特征,也可以使用连续特征。
(1)连续特征的处理
对于连续型特征,需要进行离散化处理。假设数据集![]() 有
有![]() 个样本,关于连续特征
个样本,关于连续特征![]() ,按照样本取值大小,从小到大进行排列,得到样本集关于A取值序列
,按照样本取值大小,从小到大进行排列,得到样本集关于A取值序列![]() 。CART取两个连续取值的中点作为切分点,即第
。CART取两个连续取值的中点作为切分点,即第![]() 个切分点为
个切分点为![]() ,关于连续特征
,关于连续特征![]() 的切分点一共有
的切分点一共有![]() 个。
个。
当选择第![]() 个切分点
个切分点![]() 时,左分支的样本子集为关于特征
时,左分支的样本子集为关于特征![]() 取值小于
取值小于![]() 的样本的集合,右分支的样本子集为剩余样本的集合。
的样本的集合,右分支的样本子集为剩余样本的集合。
(2)离散特征的处理
离散特征,把特征的各个取值作为切分点,例如,离散特征![]() 有
有![]() 个取值
个取值![]() ,则关于该特征共有
,则关于该特征共有![]() 个切分点。其中第
个切分点。其中第![]() 切分点,表示选择
切分点,表示选择![]() 作为特征,左分支表示关于特征
作为特征,左分支表示关于特征![]() 取值为
取值为![]() 的样本的集合,右分支为剩余样本的集合。
的样本的集合,右分支为剩余样本的集合。
3. CART分类树
当预测值为连续值时,生成CART分类树。CART分类树采用基尼系数(Gini)进行分类特征的选择。
基尼系数(Gini)反映的是数据集的纯度,表示的是直接从数据集中随机抽取两个样本,这两个样本属于不同类别的概率。基尼系数越小,表示数据集的纯度越高。
(1)基尼系数计算公式
假设数据集![]() 有
有![]() 个类别,其基尼系数的计算公式如下:
个类别,其基尼系数的计算公式如下:
以离散型特征为例,假设特征![]() ,有
,有![]() 个取值,分别为
个取值,分别为![]() ,若选择特征
,若选择特征![]() 取值为
取值为![]() ,则将数据集
,则将数据集![]() 划分成两个子集
划分成两个子集![]() (左分支,特征
(左分支,特征![]() 取值为
取值为![]() )和
)和![]() (右分支,特征
(右分支,特征![]() 取值不等于
取值不等于![]() ),则数据集选取该特征进行分类后的基尼系数如下:
),则数据集选取该特征进行分类后的基尼系数如下:
(2)特征选择
针对所有特征的所有取值,选择基尼系数最小的特征取值作为当前切分点,即
![]()
4. CART回归树
当预测值为离散值时,生成CART回归树。CART回归树采用平方误差(MSE)作为特征选择的准则。
平方误差标示的预测值与真实值之差的平方的期望。平方误差越小,说明模型拟合的越好。
(1)平方误差计算公式
假设数据集![]() 关于特征
关于特征![]() 的切分点为
的切分点为![]() (离散型特征为具体值,连续特征为按照取值从小到大的序列,具体可参考第2部分特征处理的内容)。以连续型特征为例,若选择连续特征
(离散型特征为具体值,连续特征为按照取值从小到大的序列,具体可参考第2部分特征处理的内容)。以连续型特征为例,若选择连续特征![]() 的切分点
的切分点![]() ,将数据集划分成
,将数据集划分成![]() (左分支,特征
(左分支,特征![]() 的取值小于
的取值小于![]() 的样本集合)和
的样本集合)和![]() (右分支,剩余样本的集合)两个子集。数据集选取该特征进行切分时的平方误差如下:
(右分支,剩余样本的集合)两个子集。数据集选取该特征进行切分时的平方误差如下:
其中, ![]() 表示样本子集
表示样本子集![]() 的预测值,
的预测值, ![]() 表示样本子集
表示样本子集![]() 的预测值。
的预测值。
(2)特征选择
针对所有特征的所有取值,选择平方误差最小的特征取值作为切分点,即
其中,![]() 表示样本子集
表示样本子集![]() 的预测值,
的预测值, ![]() 表示样本子集
表示样本子集![]() 的预测值。
的预测值。
(3)样本预测值
针对某个切分点,要使得切分后的平方误差最小,只需切分后的两个样本子集的平方误差均最小即可。根据一元二次方程求最小值的策略,可知:
![]()
即![]() 等于样本子集
等于样本子集![]() 的真实值的均值,
的真实值的均值,![]() 为样本子集
为样本子集![]() 的真实值的均值。
的真实值的均值。
5. CART树的构建
输入:训练数据集![]()
输出:CART树![]() (分类树or回归树)
(分类树or回归树)
根据训练数据集,从根节点开始,递归地对每个节点进行以下操作,构建二叉决策树:
① 如果当前节点的样本数小于阈值,或者没有多余的特征时,停止递归,返回决策子树;
② 对于分类树来说,如果全部样本均为同一类别时,停止递归,返回决策树;
③ 如果计算出来的特征选择准则(分类树:基尼系数,回归树:平方误差)小于阈值,停止递归,返回决策子树;
④ 针对当前节点的全部特征的全部切分点,计算每个特征每个切分点的特征选择准则(分类树:基尼系数,回归树:平方误差);
⑤ 选择特征选择准则(分类树:基尼系数,回归树:平方误差)最小的切分点作为最有切分点,将数据集切分成两个子集![]() ,生成两个左右两个子节点。
,生成两个左右两个子节点。
⑥ 针对上述两个子节点,递归地调用①-⑤步,生成CART决策树。
6. 剪枝策略
一个完全完全生长的决策树,可能会发生过拟合,即在进行预测值,效果比较差。因此,需要对决策树进行剪枝,从而提高模型的泛化能力。
(1)预剪枝与后剪枝
决策树的剪枝方式有两种,分别是预剪枝和后剪枝。
预剪枝:在决策树生成过程中进行剪枝。预剪枝停止决策树生长的方法有如下三种:
① 决策树达到预先设定的深度;
② 当前结点的样本数小于预先设定的阈值;
③ 在选择新的特征进行分裂时,需要在验证集上计算分裂前后的损失函数值(或精度),如果分裂后损失函数值变得更大(或者精度降低),则需要进行剪枝,不在进行分裂。若为分类问题,叶子结点的预测值为样本数量最多的类别;若为回归问题,叶子结点的预测值为样本标签的均值。步骤如下:
① 将当前节点标记为叶结点,计算验证集精度。
② 基于特征选择准则,进行分裂点的选取,并在验证集上计算划分后的精度。
③ 比较划分前后的精度,如果划分后精度增大,则进行划分,否则不进行划分。
预剪枝的优点是降低过拟合的风险,减少决策树的训练时间开销和预测时间开销,适合解决大规模问题;缺点是基于“贪心策略”,可能得不到最优解,有欠拟合的风险。
后剪枝:首先,训练生成一颗完整的决策树,然后按照自底向上(或自顶向下)的方式进行剪枝。将以当前结点作为叶结点的子树进行剪枝,用一个叶子结点进行代替。若为分类问题,叶子结点的预测值为样本数量最大的类别;若为回归问题,预测值为样本标签的均值。计算剪枝前后的损失函数值(或精度),若剪枝后,损失函数值得到下降(或精度得到提升),则进行剪枝,否则,保留该结点。步骤如下:
① 计算当前决策树的精度(或损失函数值);
② 对以当前结点为叶结点的子树进行剪枝,以一个叶结点代替;
③ 计算剪枝后的决策树的精度(或者损失函数值)。
常见的后剪枝方法包括错误率降低剪枝(Reduced Error Puring,REP,例如西瓜书的后剪枝方法)、悲观剪枝(Pessimistic Error Pruning,PEP)、代价复杂度剪枝(Cost Complexity Pruning, CCP,例如CART树剪枝方法)、最小误差剪枝(Minimum Error Pruning, MEP)、CVP(Critical Value Pruning)、OPP(Optimal Pruning)等方法,这些剪枝方法各有利弊,关注不同角度的优化。
后剪枝的优点是能够保持更多的分支,基于全局最有策略,出现欠拟合的风险很小,泛化性能往往由于预剪枝。缺点是需要更大的训练时间开销。
(2)CART剪枝策略
I. 损失函数
CART决策树采用的损失函数如下:
![]()
其中,![]() 表示的是对训练数据的预测误差(如分类树,可以使用基尼系统等);
表示的是对训练数据的预测误差(如分类树,可以使用基尼系统等);![]() 表示的是树的叶结点个数,也就是树的复杂度;
表示的是树的叶结点个数,也就是树的复杂度;![]() 为超参数,用来权衡训练数据的拟合度以及模型的复杂度。
为超参数,用来权衡训练数据的拟合度以及模型的复杂度。![]() 表示在参数为
表示在参数为![]() 时,树
时,树![]() 的整体损失。
的整体损失。
对于固定的![]() ,一定存在使得损失函数
,一定存在使得损失函数![]() 最小的子树(以树
最小的子树(以树![]() 的根结点为根结点,剪去以部分内部结点为根结点的子树后,得到的子树),表示为
的根结点为根结点,剪去以部分内部结点为根结点的子树后,得到的子树),表示为![]() 。
。![]() 在损失函数
在损失函数![]() 最小的意义下是最优的。容易验证这样的子树是唯一的。当
最小的意义下是最优的。容易验证这样的子树是唯一的。当![]() 大的时候,最优子树
大的时候,最优子树![]() 偏小;当
偏小;当![]() 小的时候,最优子树
小的时候,最优子树![]() 偏大。极端情况,当
偏大。极端情况,当![]() 时,整体树是最优的。当
时,整体树是最优的。当![]() 时,根结点组成的单结点树是最优的。
时,根结点组成的单结点树是最优的。
II. 代价复杂度剪枝(CCP)
CART决策树采用后剪枝策略中的代价复杂度(CCP)剪枝方法进行剪枝,分成两步;采用留出法进行模型评估,即留出一部分数据用作“验证集”以进行性能评估。第一步是,采用自底向上的方式计算每个结点的损失函数,然后按照自顶向下的方式进行剪枝,剪掉当前结点为根结点的子树,直到根节点,得到一个列子树系列![]() 。第二步是,在验证集上采用交叉验证方法,对子树序列进行测试,从中选择最优子树。
。第二步是,在验证集上采用交叉验证方法,对子树序列进行测试,从中选择最优子树。
第一步:剪枝,形成一个子树序列
Breiman等人证明:可以用递归的方法对树进行剪枝。将![]() 从小增大,
从小增大,![]() ,产生一系列的区间
,产生一系列的区间![]() ;剪枝得到的子树序列对应着区间
;剪枝得到的子树序列对应着区间![]() 的最优子树序列
的最优子树序列![]() ,序列中的子树是嵌套的。
,序列中的子树是嵌套的。
具体地,从整体树![]() 开始剪枝。对
开始剪枝。对![]() 的任意内部结点
的任意内部结点![]() ,以
,以![]() 为单结点树的损失函数是
为单结点树的损失函数是
![]()
以![]() 为根结点的子树
为根结点的子树![]() 的损失函数是
的损失函数是
![]()
当![]() 及
及![]() 充分小时,有不等式
充分小时,有不等式
![]()
当![]() 增大时,在某一
增大时,在某一![]() 有
有
![]()
当![]() 再增大时,不等式反向。只要
再增大时,不等式反向。只要![]() ,
,![]() 与
与![]() 有相同的损失函数值,而
有相同的损失函数值,而![]() 的结点少,因此
的结点少,因此![]() 比
比![]() 更可取,对
更可取,对![]() 进行剪枝。
进行剪枝。
为此,对![]() 中每一个内部结点
中每一个内部结点![]() ,计算
,计算
它表示剪枝后整体损失函数减少的程度。在![]() 中剪去
中剪去![]() 最小的
最小的![]() ,将得到的子树作为
,将得到的子树作为![]() ,同时将最小的
,同时将最小的![]() 设为
设为![]() 。
。![]() 为区间
为区间![]() 的最优子树。
的最优子树。
如此剪枝下去,直至根结点。在这一过程中,不断增加![]() 的值,产生新的区间。
的值,产生新的区间。
第二步,在剪枝得到的子树序列![]() 中通过交叉验证选取最优子树
中通过交叉验证选取最优子树![]() 。
。
具体地,利用独立的验证集,测试子树序列![]() 中各个子树的平方误差或基尼系数。平方误差或基尼系数最小的决策树被认为是最优的决策树。
中各个子树的平方误差或基尼系数。平方误差或基尼系数最小的决策树被认为是最优的决策树。
具体操作步骤如下:
输入: CART算法生成的决策树![]()
输出:最优决策树![]()
① 设![]() ;
;
② ![]() ;
;
④ 自上而下地访问内部结点![]() ,如果有
,如果有![]() ,进行剪枝,并对结点
,进行剪枝,并对结点![]() 以多数表决(分类)或者取标签值的平均值(回归)得到叶子结点标签,得到决策树
以多数表决(分类)或者取标签值的平均值(回归)得到叶子结点标签,得到决策树![]() ;
;
⑤ 设![]() ;
;
⑥ 如果![]() 不是由根结点和两个叶子结点构成的树,则回到步骤②;否则,令
不是由根结点和两个叶子结点构成的树,则回到步骤②;否则,令![]() ,进行下一步。
,进行下一步。
⑦ 采用交叉验证法在验证集上进行验证,在![]() 中选取最优子树
中选取最优子树![]() 。
。
7. 分类树类别不平衡处理机制
CART分类树对类别不平衡的情况做了处理,无需用户干预。它采用先验机制,计算每个结点关于根结点的类别频率的比值,作用相当于对类别进行加权。以二分类为例,结点(node)被分类成为1的条件是![]() 。
。
附录:
1. 机器学习之分类与回归树(CART)
2. 决策树算法--CART分类树算法 - 知乎
3. 分类回归树 ( CART) - 简书
4. 决策树剪枝:预剪枝、后剪枝_WellWang_S的博客-CSDN博客_预剪枝和后剪枝
5. 第4.2章:决策树(decision tree)_决策树的剪枝&优缺点_popo-shuyaosong的博客-CSDN博客_决策树剪枝会导致预测效果下降
6. 李航《统计学习方法》
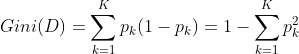
![min_{A, a} \left [ min_{c_{1}} \sum_{x_{i} \in D_{1}} \left ( y_{i} - c_{1}\right ) ^ 2 + min_{c_{2}} \sum_{x_{i} \in D_{2}} \left ( y_{i} - c_{2}\right ) ^ 2 \right ]](http://img.e-com-net.com/image/info8/24e653c77404425d8e571769991584f0.gif)