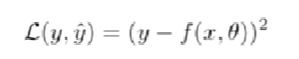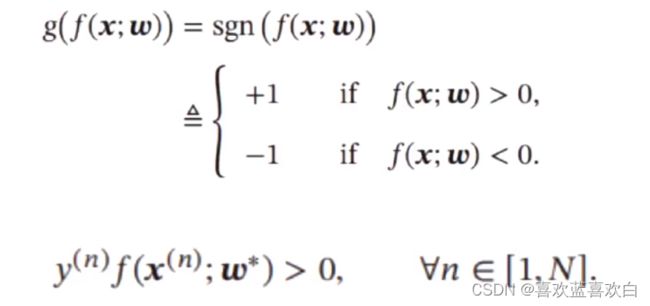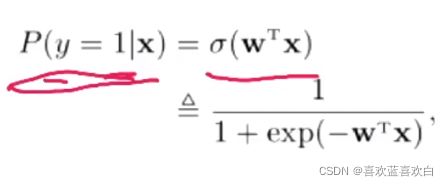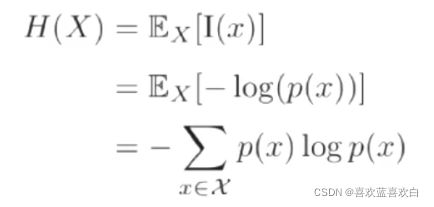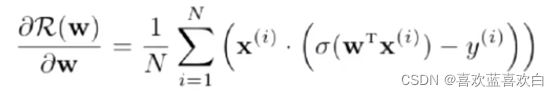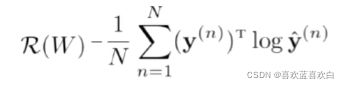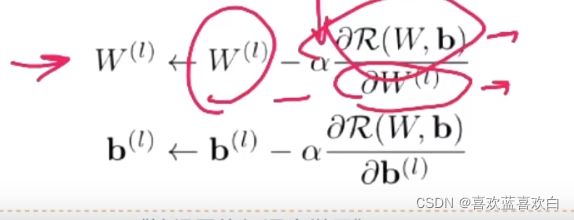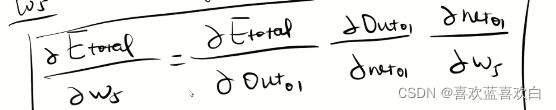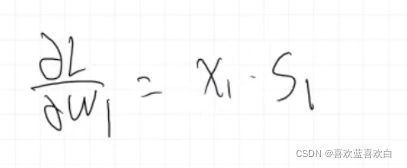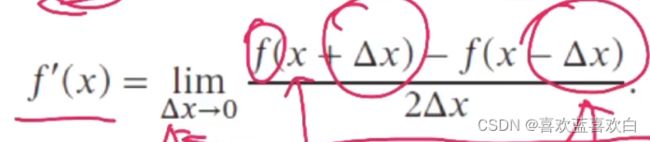喜欢蓝喜欢白

《神经网络与深度学习》基础篇

此文为看视频后个人见解，原著请看：神经网络与深度学习理论与实战-TensorFlow2.0_哔哩哔哩_bilibili本课程的目的是争取让零基础的同学也能理解深度学习的相关知识，理解代码的编程思路。课程中的很多素材都来自网络，特别感谢邱锡鹏老师的《神经网络与深度学习》和网易云课堂龙龙老师的《深度学习》，还有csdn、知乎等平台上的众多文章，在此一并表示感谢。如有侵权，请联系我删除（b站写私信给我）。本人能力水平非常有限，课程中难免有各种错误，请大家多多指正，多多包涵。想了解 TenosrFlow 更多新功能，可点https://www.bilibili.com/video/BV155411t7ad

一：机器学习基础

1.1 机器学习的三要素

1.1.1. 模型

1.1.2.1. 学习准则-损失函数。

1.1.1.2. 学习准则-参数学习

1.2. 梯度下降法

1.2.1. 原理及种类

1.2.2. 随机梯度下降法（实战）

1.3. 线性回归

1.3.1. 经验风险最小化-最小二乘法：

1.3.2. 经验风险最小化-岭回归

1.3.3. 从概率的角度看待线性回归

1.3.4. 最小二乘法求二元线性回归回归（实战）

二：线性模型

2.1. 分类介绍

2.2. 线性模型处理分类问题

2.3. 二分类问题

2.4. 多分类

2.5. 从概率角度看待分类问题

2.5.1. 多元线性回归进行分类产生的问题

2.5.2. 从概率角度解决分类问题

2.6. 交叉熵

2.6.1. 信息量的数学期望就是熵

2.6.2. 相对熵

2.7. 逻辑回归（实战）

2.8. softmax

2.8.1. 理论

2.8.2. softmax（实战）

2.9. 感知器

2.9.1. 感知器理论

2.9.2. 感知器（实战）

2.10. 用softmax回归进行MNIST数据集的手写数字识别（实战）

三：前馈神经网络

3.1. 神经元与激活函数

3.2. 全连接神经网络（前馈神经网络/多层感知器）介绍

3.3. 反向传播算法

3.4. 自动梯度计算

3.5. Himmelblau函数求极小值（实战）

3.6. 全连接神经网络MNIST分类（实战）

四：TF2 基础（实战）

4.1. 变量与张量介绍

4.2. 张量的计算与转换

4.3. 张量的合并与分割

4.4. 张量的数据统计

4.5. 张量的填充与复制

4.6. tf.gather()

4.7. tf.boolean_mask()

4.8. tf.where(cond,x,y)

4.9. scatter_nd(indices,updates,shape)

4.10. tf.meshgrid()

4.11. 数据集加载与预处理

五：Keras高层接口

5.1. 模型的装配、训练和测试

5.2. 模型的装配、训练与测试

5.3. 模型的保存和加载

5.4. 自定义网络层类

5.5. 测量工具和可视化

六：卷积神经网络

6.1. 全连接神经网络存在的问题

6.2. 卷积是什么？

6.2.1. 1D卷积

6.2.2. 2D卷积

6.2.3. 卷积扩展-步长和填充

6.3. 通道与卷积核

6.3.1. 单通道-单卷积核

6.3.2. 多通道-单卷积核

6.3.3. 多通道-多卷积核

6.4. 卷积运算（实战）

6.4.1. 卷积计算

6.5. 池化层

6.6. 卷积网络结构

6.7. 梯度计算

6.8. LeNet-5（实战）

6.9. AlexNet -------第一个现代深度卷积网络模型（理论+实战）

6.10. BN （理论+实战）

6.11. VGG （理论+实战）

6.12. GoogleNet（理论+实战）

6.13. ResNet（实战）

6.14. 卷积的变种、应用、总结

七：循环神经网络

7.1. Embedding

7.2. RNN介绍

7.2.1. memory机制

7.3. SimpleRNN （实战）

7.4. 循环神经网络的问题

7.5. LSTM

7.6. LSTM层在情感分类（实战）

7.7. GRU （理论+实战）

一：机器学习基础

1.1 机器学习的三要素

1.1.1. 模型

首先明确机器学习的主要任务：确定样本空间的输入x和输出y，及x和y之间找到一个f(x, $\Theta$ ) -> y。的模型f(x, $\Theta$ ) ，且尽可能与输出y相匹配。一开始不知道这样的函数是什么样的，所以我们要g根据经验，假设有一个函数集合（f1,f2,f3,f4,f5……，fn），这样的假设函数集合有时候也成为假设空间，我们通过观察，这一系列函数，在训练集中的表现，来选取一个fi在训练集D中最理想，那么fi就是最适合的，或者说是最理想的假设。

我们常说的模型有：

线性模型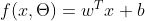： $f(x,\Theta ) = w^{T}x + b$ ，是一个参数化的线性函数族。
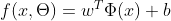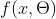广义线性方法： $f(x,\Theta ) = w^{T}\Phi (x) + b$ ,其中 $\Phi (x)$ 为可学习的非线性基函数， $f(x,\Theta )$ 就等价于神经网络。

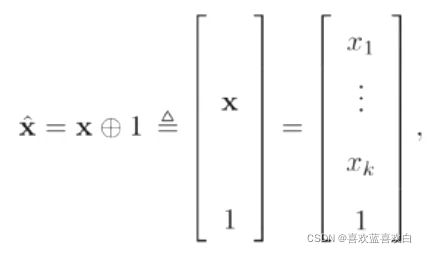
线性模型：w是一个权重向量，x是一个特征向量，w的转置与X相乘，得到一个值再与b相加即为当前模型下的预期值y^。

非线性模型：x经过一个非线性的函数 $\Phi (x)$ ，可以得到一个非线性的特征向量 $[\Phi (x_{1}) ,\Phi (x_{2}) , \Phi (x_{3}) , ....... , \Phi (x_{n})]$ ，而 $\Phi (x)$ 又是一个可以学习的非线性基函数，则 $\Phi (x)$ 可以再套一层非线性基函数。依次类推。

经过多层学习基函数后得到的向量，又可以作为新的输入x继续重新进行训练，这与全连接神经网络有异曲同工之妙。

1.1.2.1. 学习准则-损失函数。

我们有，训练集D，模型 $f(x,\Theta )$ 。现在将测试集放入模型 $f(x,\Theta )$ 中得到一个结果y^，再拿预测值y^与真实值y作比较。而作比较的手段即学习准则。

通常思路是：得到所有预测值y^ 与真实值y之间的差值绝对值之和，我们要尽可能使这个和小于一定值，则满足要求。若是概率也是类似。

所以说我们要度量一个模型的好坏，需要引入一个期望风险（expected risk）的概念。期望的风险是一个数学期望。即 $R(\Theta ) = E( L(y,f(x,\Theta )))$ ,我们求的数学期望是Loss函数（损失函数）的期望。

损失函数有很多种类，如：

0-1损失函数：

数学性质不太好（倒数 = 0），所以我们需要一个连续可微的损失函数。如平方差损失函数

平方差损失函数：

平方损失函数一般用在结果为实值上，即连续的值，但不适合分类，即离散的值。一般会使用交叉熵损失函数（又称为负的对数似然函数 ,将实值之间的比较转换成概率值之间的比较）。

还有一种二分类损失函数Hinge：L= max(0 , 1 - y * y^)，若y与y^相近则正负性相同，相乘为正，1 减去一个大于0 的数则 loss值相对较小。

1.1.1.2. 学习准则-参数学习

由以上可以得出，我们在寻找一个适合的模型，评判标准就是这个模型 $f(x,\Theta )$ 在数据集上有一个比较小的期望风险。期望风险是在训练集和测试集上共同的得到的风险加到一起。而我们只能在训练集上做这些预测，测试集的东西是未知的，因此期望风险是未知的，一般通过在一部分数据集上预测的结果即经验风险，来近似。

利用经验风险，在局部上逐步取得最优化：

$R(\Theta ) = \frac{1}{N}\sum_{n=1}^{N}L(y^{n},f(x^{n},\Theta ))$

经验风险最小化

在选择合适的风险函数后，我们寻找一个参数 $\Theta ^{*}$ ，使得经验风险最小化。
机器学习转化为一个最优化问题：

当在训练集上通过更新参数，不断最小化经验风险的方法，是一个不断拟合的过程。

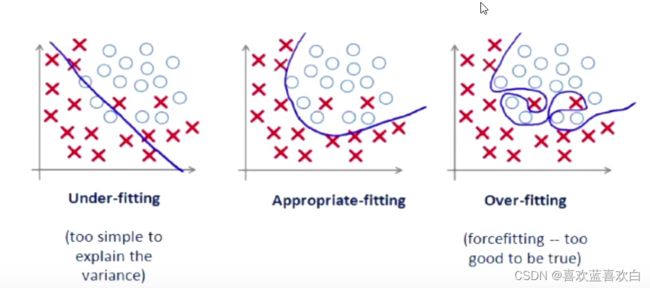
过拟合：模型过于复杂，在训练集上训练的还行，在测试集不一定可以。一般由于数据少或者噪声的影响。
欠拟合：在训练集上表现得不好，在测试集上也可能表现得不好。

因此我们需要找到一个中间的状态，如下图中的第二张图片。

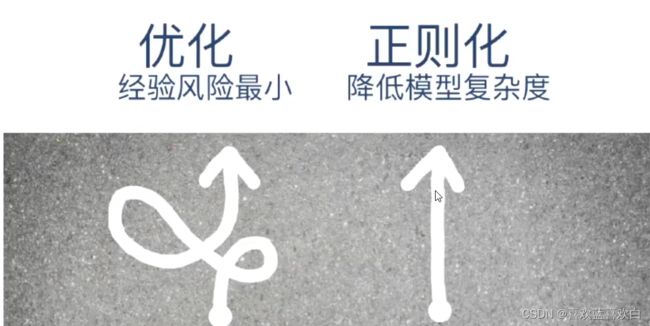
增强泛化能力：

正则化后，模型适合更多数据，且降低模型复杂度，何为正则化，所有损害优化的操作都是正则化！有1.增强约束，如增加L1/L2约束，2.干扰优化过程，如提前终止优化。

1.2. 梯度下降法

1.2.1. 原理及种类

我们之前提及，机器学习是一个最优化的问题，那最优化有何种途径呢？一个很直接的方法就是梯度下降法，逐步找到最小值。

图中曲线是一个凸函数(这里的凸函数与国内考研教材凸函数定义相反)： $R(\Theta )$ ，我们如何更新参数使得风险函数最小呢？

假设曲线中某一点的斜率（导数或偏导）为负数，那原来的 $\Theta$ 就会减去一个负数，从而向右移动，即向使得风险函数更小的方向移动。相同的，假如该点斜率为正数，那么就会减去一个负数， $\Theta$ 就会往左移动。其中的 $\alpha$ 是学习率。

学习率的取值也是一个很关键的因素，以下图片总结：

上面提到的 $\Theta$ 是一个通过样本可学习的参数，不是我们定义的，通常模型的性质中会包含。而 $\alpha$ 是我们定义的，这里是指一次学习速度的快慢，我们把这种自己定义的，与模型无关，但是在训练过程中又能对模型的训练起到至关重要作用的参数成为超参，像这样的参数还有网络的层数，聚类的个数，分类的个数等。

梯度下降法分为：

批量随机下降法（BGD）：每个样本都要进行更新。
随机梯度下降法（SGD）：每次都是取随机的对一个样本更新，对那种不完全是凸函数的模型有时会找到相对于批量随机下降法更好的参数。但不利于利用计算机的并行能力。
小批量的随机梯度下降法：随机取出其中的一堆，进行更新。

1.2.2. 随机梯度下降法（实战）

图片来源于网课截图。

import numpy as np
X = np.arange(0,50)
# RandomArray是 [-5,5)的噪声值
np.random.seed(1)#让每次取到的随机值都是一样的。
RandomArray = (np.random.random(50)*2-1)*5

y  = 2 * X + RandomArray

import matplotlib.pyplot as plt
plt.scatter(X,y)

X = X.reshape(50,1)
y = y.reshape(50,1)
#把X,y连接起来，第一个值是特征值，第二个值是标签
All_date = np.concatenate((X,y),axis = 1)#默认的是第一个维度即按行，这里要按列
All_date #此时数据集完成！

np.random.shuffle(All_date)

train_date = All_date[:40]
test_date = All_date[40:]
np.sum(All_date[:,0] * 2 - All_date[:,1]) # 所有 x - y 值的和 后面的0，1 是维度。

# 超参初始化
lr = 0.001 #学习率
N = 100
epsilon = 195
randint = np.random.randint(0,40)#随机的一个索引。
rand_x = train_date[randint][0] # x值是第一个值，因此取 0
rand_y = train_date[randint][1] # y是第二个值，同理

#要学习的参数
theta = np.random.rand()
theta

#开始训练（核心代码）
Num = 1
theta_list = []
loss_list=[]
while True:
    #重新排序
    np.random.shuffle(train_date)
    for n in range(N):
        randint = np.random.randint(0,40)#随机的一个索引。
        rand_x = train_date[randint][0] # x值是第一个值，因此取 0
        rand_y = train_date[randint][1] # y是第二个值，同理
        #先要计算梯度，在此基础上更新参数，
        # 1.计算梯度
        grad = rand_x * (rand_x *theta -rand_y)
        # 2.更新参数theta
        theta = theta - lr * grad
    #计算更新theta后的错误率
    X = train_date[:,0]#同下。
    y = train_date[:,1] # 是不是应该用测试集？？
    loss = np.sum(0.5*(theta*X -y)**2)
    print("Number: %d,theta %f loss: %f"%(Num,theta,loss))
    Num = Num + 1
    theta_list.append((theta))
    loss_list.append(loss)
    if loss < epsilon :
            break
# 画图
plt.plot(range(len(theta_list)),theta_list)
plt.plot(range(len(loss_list)),loss_list)

1.3. 线性回归

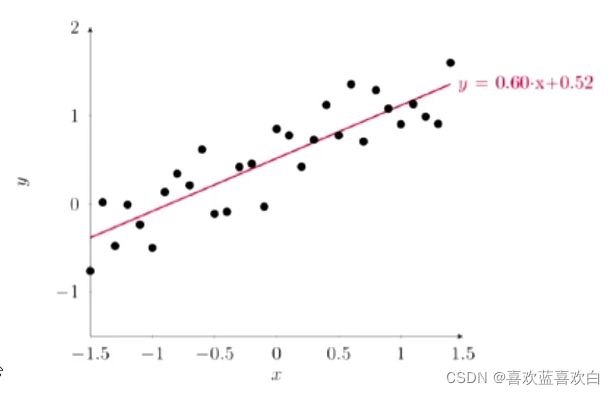
之前的模型x即特征只有一种，但一般情况肯定不会只有一种，当样本维度为1时，我们成为简单回归（左图）；当特征有很多个的时候，即x有很多维度时，我们就说他是多元回归（右图）。

模型： $f(x;w,b) = w^{T}x + b$
增广权重向量：
增广特征向量：

（ 2和3共同组成了 $f(x;\hat w) = \hat{w}^{T}\hat{x}$ 。）

优化方法：

实值：经验风险最小化，结构风险最小化。
概率值：最大似然估计值，最大后验估计。

1.3.1. 经验风险最小化-最小二乘法：

模型： $f(x;w) = w^{T}x + b$
学习准则：损失函数可以用平方差函数。只在训练集上训练，即经验风险，经验风险最小化经验风险最小化，即希望预测值与真实值尽可能最小化。即希望 $R(w) =\sum_{n=1}^{N}L(y^{n},f(x^{n},w))$ 最小，经验风险也可以转换为范数形式: $\frac{1}{2}\left \| y - X^{T}w^{(n)} \right \|$

（范数：向量空间种度量一个向量的长度或大小。如1范数是所有向量绝对值之和。2范数是所有向量平方和再开根号，也叫欧几里得范数。）

优化：，

以上提到的优化方法是最小二乘法，需要存在逆矩阵，即保证每个数据是独立的。但是不能保证每个数据特征是独立的，因此最小二乘法有很多约束。

1.3.2. 经验风险最小化-岭回归

为了解决最小二乘法造成的影响，我们引入了岭回归的概念，给 $XX^{T}$ 的对角线加上一个常数，这样就保证其满秩，即相互独立。原来： $w^{*} = (XX^{T})^{-1}Xy$ ，变为： $w^{*} = (XX^{T} + \lambda I)^{-1}Xy$ ，其中I是一个单位矩阵。经过整理最后风险函数变为： $\frac{1}{2}\left \| y - X^{T}w^{(n)} \right \|^{2} + \frac{1}{2}\lambda \left \|w \right \|^{2}$ 。我们也可以理解为，对影响最大的权重进行正则化。

1.3.3. 从概率的角度看待线性回归

此部分已经在另一板块花了好几天总结，在此省略。

值得一提的是，之前最小二乘法用梯度下降法求参数是寻找经验风险最小值，而类似于正态分布这种凹函数，用梯度下降法最后求得的是极大值！也正好符合我们需要求参数取何值时下，样本在某模型上表现得更好的需求！

1.3.4. 最小二乘法求二元线性回归回归（实战）

import numpy as np;

np.random.seed(1)
X = np.random.normal(size = (1000,2),scale = 1) # X1，X2
X

RandomArray =(np.random.random(1000)*2 - 1)*5
y  = 2 * X[:,0] + (-3)*X[:,1] + 4 + RandomArray

import matplotlib.pyplot as plt
plt.scatter(X[:,0],y)

plt.scatter(X[:,1],y)

from mpl_toolkits import mplot3d
ax = plt.axes(projection = '3d')
ax.scatter3D(X[:,0],X[:,1],y)

All_date = np.concatenate((X,y.reshape(1000,1)),axis = 1)
All_date

#构造训练集和测试集
np.random.shuffle(All_date)
train_date = All_date[:700,:]
test_date = All_date[700:,:]
train_date.shape,test_date.shape

W = np.random.normal(size = (2))
b = np.random.rand()
W[0],W[1],b

loss = 0.5 * np.sum( (y - (2*X[:,0] + (-3)*X[:,1] + 4)) ** 2)

#计算当前模型的损失值
loss = 0.5*np.sum( (y -(W[0]*X[:,0]+ W[1]*X[:,1] + b))**2 )

X = train_date[:,:2]
X = X.reshape(2,700)
y = train_date[:,-1]
X.shape

#构建增广矩阵
W_hat = np.concatenate((W,np.array([b]))).reshape(3,1)
X_hat = np.concatenate((X,np.ones((1,700))),axis = 0)
W_hat.shape,X_hat.shape

W_hat,X_hat

np.sum((y.reshape(700,1) - np.dot(X_hat.T,W_hat))**2)/700

lr = 0.0001 # 学习率
Num = 1
w0_list = []
w1_list = []
b_list = []
loss_list = []

while True:
    #训练集上更新参数
    W_hat = W_hat + lr * np.dot(X_hat,(y.reshape(700,1) - np.dot(X_hat.T,W_hat)))
    #记录参数
    w0_list.append(W_hat[0])
    w1_list.append(W_hat[1])
    b_list.append(W_hat[2])
    # 训练集上计算总错误
    loss = np.sum((y.reshape(700,1) - np.dot(X_hat.T,W_hat))**2)/2
    loss_list.append(loss)
    if Num % 10 == 1 :
        print("Number: %d, loss: %f"%(Num,loss))
    Num = Num + 1
    if loss < 1000 or Num >1000:
        break

plt.plot(range(len(loss_list)),loss_list)
plt.plot(range(len(w0_list)),w0_list)
plt.plot(range(len(w1_list)),w1_list)
plt.plot(range(len(b_list)),b_list)

二：线性模型

线性模型（line model），之前已经接触过很多次。它主要是通过把样本的特征线性组合，然后在进行一个预测。线性模型反应了机器学习非常重要的一个思路：从错误中学到知识或经验，关键是正确的认识错误。

之前都是预测一个实值，或找到一个概率。总而言之都是找到一个值（预测或回归问题）。接下来，都是总结线性模型在分类上的应用。

2.1. 分类介绍

怎么把实值转换成一个离散的值（离散的值能表示具体的分类，如判断是猫还是狗，结果是1就是猫，0就是狗。）？我们需要引入一个决策函数（有时称为符号函数），如把f(x)作为自变量进过决策函数g(f(x))运算后就转换为一个离散值。

如：狗，猫，猴概率值是{0.2,0.9,0.1}，那么可以认为输出就是猫。

让原来的线性模型输出一个非线性的输出。

2.2. 线性模型处理分类问题

之前的实战的内容都是特征只有一种的，即在二维坐标中的一条线。

但在真正分类的过程中，要识别出一个物品，我们需要依据他很多的特征，即X (X1,X2……)，把这个X经过线性模型输出的结果在经过几个决策函数，就可以得到一个分类的结果。

如图，x有很多个特征，b是偏执项。右图是二者相加得到的增广权重矩阵乘以增广特征矩阵，后将结果经过一个决策函数，最后得到一个结果。最后在经过分类器可以得到分类结果。

2.3. 二分类问题

下图右图，连坐标轴表示的是两个特征。假如是一分类就是一个坐标轴。

二分类就是要找到一条线y = w1*x1 + w2*x2 + b = 0，把两个特征给分开，下图右图就是把实心圆和空心圆分开。

怎么分呢？把样本点带进y中，最后得出结果若小于0，则是线下方的值，大于0则是上方的值，这里的决策函数就是左图所示。最后得到了两种离散值，这就是决策函数的功能。

为什么把结果带进去之后大于0小于0就能直接分类呢？我们可以通过求距离公式，距离公式的分子就是w1**2 + w2**2再开根号，也就是其二范式。其>0最终就是取决于分子是否大于0.

2.4. 多分类

一对其余：用一条直线将一个与其他所有分开，假如有c个特征的话，我们需要c条直线将其分开。但缺点就是，会有少数点不能区分是哪一类。

一对一：用c（i，j）表示类别i和类别j之间的区分，这样根据排列组合，我们需要c（c-1）/ 2条直线将其分开。

“argmax”方式：一种改进的一堆其余的方式，C个特征共需要C个判别式，求出每个样本是所有类别的可能性，最终取最大可能的类别。

2.5. 从概率角度看待分类问题

2.5.1. 多元线性回归进行分类产生的问题

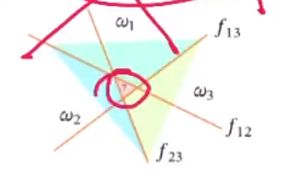
无法处理极度离群的样本，如下图红圈内的差本应该出现在直线右边，但此时彻底的在左边。

无法处理非线性的分类：如下图圈和差。

2.5.2. 从概率角度解决分类问题

为了解决线性函数不适合进行分类的问题，我们引入非线性函数g来预测表情的后验概率,即f(x;w) = x时，标签取c的概率是多少。p既然是概率那么一定就是一个[0,1]的值。

则我们可以想象，我们引入的非线性函数一定是一个可以把f（x；w）挤压到[0,1]的函数。

接下来举例介绍1个这样的非线性函数：

Logistics函数（sigmoid函数）： $\frac{1}{1+e^{-x}}$ 。（这是s族函数中的一种，用得比较多。）

在sigmoid的基础上，在f（x；w） = x时，目标类别y = 1的概率又可以表示为：

模型有了，那么学习准则用什么表示呢？

真实值：
预测值：

怎么衡量这两个条件分布之间的差异呢？这时就可以利用交叉熵了！

2.6. 交叉熵

如以上所讲，在机器学习中，交叉熵就是用来评价目标概率和真实概率之间的差异。在信息论中，交叉熵用来衡量一个随机事件的不确定性。

在理解交叉熵之前，我们理解一下信息量的概念

2.6.1. 信息量的数学期望就是熵

比如说，我们听说了两件事，狗咬人，第二件事，人咬狗。在可能性上，狗咬人的可能性比人咬狗的时间可能性大。在信息量上，我们认为狗咬人不算是什么特别的事，人们之前就知道了，获取的信息量可以认为很低，但是若发生了人咬狗事件，则认为信息量很大。因此，我们认为，可能性和信息量刚好呈一个反比。

那么我们现在假设X是一个试验，x1离散型的随机变量是实验X中的一个可能事件，设x发生的概率为p(x) = p(X = x)，那么信息量可以为 $I(x_{1}) = -log(p(x))$ ，但x = 1时，ln(x) = 0即信息量为0，但x = 0时，信息量无限趋近于正无穷。

则熵是什么呢？一个事情可能有很多种可能性，每种可能性都有一种给概率。（即分类类别都有一种概率），则每个时间的概率都可以求出来一个信息量，而熵就是所有信息量的数学期望。

特殊的对于二分类问题，

2.6.2. 相对熵

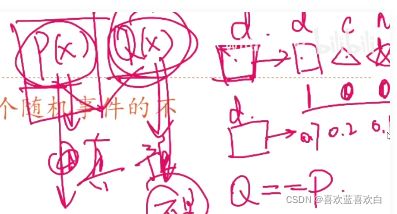
相对熵有时称为KL散度。我们真实值是：p(x),预测值是Q(x)，但预测值的离真实值还有一定距离时，我们需要增加信息量，来让Q(x)无限接近于p(x)，直到我们可以认为Q == P。KL散度就是描述Q和P接近程度的一个概念。 $D_{KL} = \sum plog(\frac{p}{q}) = \sum plog(p)-\sum plog(q)$ ，KL散度越小则认为P和Q差距较小，因为但他们越接近时，他们的比值越接近1，则KL散度就越接近0。

KL散度的计算公式中第一个元素 $\sum plog(p)$ 就是每个事件的信息量*这个信息量的概率之和，即熵，是我们选取样本后知道的，确定的固定值，也就是说这个p是已知的。而在相对熵中我们不知道的就是q，即预测值。因此我们可以把KL散度的公式中的前半部分给移去，只留下后半部分， $H(p,q) = -\sum plog(q)$ 来描述p和q之间是否接近。而这个H(p,q)就是交叉熵！！！

交叉熵作为损失函数，模型在训练集上的风险函数为（二分类）：

这显然又是一个更新参数的过程，怎么更新呢？可以使用梯度下降法。

梯度为：

2.7. 逻辑回归（实战）

import numpy as np
import matplotlib.pyplot  as plt

#设置种子，让每次取得值都是一样的
np.random.seed(0)
Num = 100

# X(x1,x2) y 0/1
# y = 1
x_1 = np.random.normal(6,1,size=(Num))
x_2 = np.random.normal(3,1,size=(Num))
y = np.ones(Num)
c_1 = np.array([x_1,x_2,y])#如此直接拼接
c_1.shape
#np.random.normal(loc ,scale,size)
#loc:正态分布的均值，以此为中心，scale：标准差，标准差越大，曲线越矮胖，小则高瘦

x_1 = np.random.normal(3,1,size=(Num))
x_2 = np.random.normal(6,1,size=(Num))
y = np.zeros(Num)
c_0 = np.array([x_1,x_2,y])#如此直接拼接
c_0.shape

# 让表头是特征，行是样本
c_1 = c_1.T
c_0 = c_0.T

plt.scatter(c_1[:,0],c_1[:,1],marker='+')
plt.scatter(c_0[:,0],c_0[:,1])

#默认是按行拼接
All_date = np.concatenate((c_1,c_0))
All_date.shape

#一般是在第一维度打乱
np.random.shuffle(All_date)
train_date_X = All_date[:150,:2]
train_date_y = All_date[:150,-1]
text_date_X = All_date[150:,:2]
text_date_y = All_date[150:,-1]
train_date_X.shape,train_date_y.shape

# y = w*1xx1 + w2*x2 = 0
W = np.random.rand(2,1)
W

#w1 *x +w2*y = 0
plt.scatter(c_1[:,0],c_1[:,1],marker='+')
plt.scatter(c_0[:,0],c_0[:,1])
x = np.arange(10)
y = -(W[0]*x)/W[1]
plt.plot(x,y)

# 逻辑回归里，使用交叉熵作为损失函数
#定义损失函数,交叉熵
def cross_entropy(y,y_hat):
    return -np.mean( y*np.log(y_hat) + (1-y)*np.log(1-y_hat))

#y_hat = sigmoid(w*x)
def sigmoid(z):
    return 1./(1.+np.exp(-z))

#开始训练
lr = 0.001
loss_list = []
for i in range(1000):
    #计算交叉熵loss,监控一下变化情况，希望loss从大变小
    y_hat = sigmoid(np.dot(train_date_X,W))
    loss = cross_entropy(train_date_y,y_hat)
    loss_list.append(loss)
    # 计算梯度
    grad = - np.mean( (train_date_X*(train_date_y-y_hat.T).T),axis = 0 )#第一个维度上
    #在第一位都上求平均后（150，2） -> （1，2）
    #更新梯度 w参数
    W = W - (lr*grad).reshape(2,1)
    #输出
    if i%10 == 1:
        print("i: %d,loss:%f"%(i,loss))

#画图
plt.scatter(c_1[:,0],c_1[:,1],marker='+')
plt.scatter(c_0[:,0],c_0[:,1])
x = np.arange(10)
y = -(W[0]*x)/W[1]
plt.plot(x,y)

plt.plot(loss_list)

# 预测一下
# y_hat = w1*x1 +w2*x2 > 0，与真实值进行比较
y_hat = np.dot(W.T,text_date_X.T)
y_pred = np.array(y_hat>0,dtype=int).flatten()
a = text_date_y == y_pred

test_acc = np.sum(a)/a.size
test_acc

2.8. softmax

2.8.1. 理论

softmax是logistics在多分类上的推广，多分类的标签会有多个取值。而标签取c1的概率为：

分母为所有在训练集上标签取所有种类可能的概率之和。

模型确定了可以使用softmax，那风险函数呢？我们仍然可以使用交叉熵来判定。此时的交叉熵仍是所有信息量的数学期望（当然是哈哈哈，定义就是这样。）

优化方式仍然可以采用梯度下降法：

虽然书本上常看到的W权重和X特征向量都是增广向量，即加了那个偏执项。但是我们在计算的时候，往往会先计算W（参数）的偏导，即grad 再通过W = W - lr*grad的方式更新W。然后再求b的偏导，以同样的方式更新b的值。

学到这里里感觉softmax有点像贝叶斯公式，求的是一个后验概率。

2.8.2. softmax（实战）

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)
Num = 100

# y = 0
x_1 = np.random.normal(3,1,size = (Num)) # 3附近的满足高斯分布的点
x_2 = np.random.normal(-3,1,size = (Num)) # 3附近的反差为1的点
y = np.zeros(Num)
c_0 = np.array([x_1,x_2,y]) #[x1,x2]是特征,y是样本的预测值。

# y = 1
x_1 = np.random.normal(-3,1,size = (Num)) # -1附近的满足高斯分布的点
x_2 = np.random.normal(-3,1,size = (Num)) # 3附近的反差为1的点
y = np.ones(Num)
c_1 = np.array([x_1,x_2,y]) #[x1,x2]是特征,y是样本的预测值。

# y = 2
x_1 = np.random.normal(-3,1,size = (Num)) # -3附近的满足高斯分布的点
x_2 = np.random.normal(3,1,size = (Num)) # 3附近的反差为1的点
y = np.ones(Num)*2
c_2 = np.array([x_1,x_2,y]) #[x1,x2]是特征,y是样本的预测值。

# y = 3
x_1 = np.random.normal(3,1,size = (Num)) # 3附近的满足高斯分布的点
x_2 = np.random.normal(3,1,size = (Num)) # 3附近的反差为1的点
y = np.ones(Num)*3
c_3 = np.array([x_1,x_2,y]) #[x1,x2]是特征,y是样本的预测值。

c_0 = c_0.T
c_1 = c_1.T
c_2 = c_2.T
c_3 = c_3.T

plt.scatter(c_1[:,0],c_1[:,1],marker = '+')
plt.scatter(c_0[:,0],c_0[:,1],marker = '^')
plt.scatter(c_2[:,0],c_2[:,1],marker = '*')
plt.scatter(c_3[:,0],c_3[:,1])

All_data = np.concatenate( (c_0,c_1,c_2,c_3) )
All_data.shape

np.random.shuffle(All_data)

train_data_X = All_data[:300,:2]
train_data_y = All_data[:300,-1].reshape(300,1)
test_data_X = All_data[300:,:2]
test_data_y = All_data[300:,-1].reshape(100,1)

# 有四组W1，W2，则W的形状是4行2列
W = np.random.rand(4,2)

# 而b只有四个直线，因此只需定义一个1行4列的偏置值即可
bias = np.random.rand(1,4)

plt.scatter(c_1[:,0],c_1[:,1],marker = '+')
plt.scatter(c_0[:,0],c_0[:,1],marker = '^')
plt.scatter(c_2[:,0],c_2[:,1],marker = '*')
plt.scatter(c_3[:,0],c_3[:,1])
x = np.arange(-5,5)
y1 = -(W[0,0]*x + bias[0,0])/W[0,1]
y2 = -(W[1,0]*x + bias[0,1])/W[1,1]
y3 = -(W[2,0]*x + bias[0,2])/W[2,1]
y4 = -(W[3,0]*x + bias[0,3])/W[3,1]
plt.plot(x,y1,'b')
plt.plot(x,y2,'y')
plt.plot(x,y3,'g')
plt.plot(x,y4,'r')

# softmax(x) = e^x / sum(e^x)
#把所有实值转化为概率值
# 一维
def softmax1(z):
    return np.exp(z)/np.sum(np.exp(z))

a = np.array([1,2,3])
softmax1(a)

b = np.array([1,2,3,4,5,6,7,8,9]).reshape(3,3)
softmax1(b)

# 对于多行的z,即矩阵，希望softmax的分母是当前行的exp之和
def softmax(z):
    exp = np.exp(z)
    sum_exp = np.sum(np.exp(z),axis = 1,keepdims=True)
    return exp/sum_exp

softmax(b)

def one_hot(temp):
    one_list = np.zeros((len(temp),len(np.unique(temp) )))
    one_list[np.arange(len(temp)) , temp.astype(np.int).T] = 1
    return one_list

one_hot(train_data_y)

# 计算 y_hat
def compute_y_hat(W,X,b):
    return np.dot(X,W.T) + b

# 计算交叉熵
def cross_entropy(y,y_hat):
    return -(1/len(y))*np.sum(y*np.log(y_hat))

# w = w - lr*grad
lr = 0.01
loss_list = []
for i in range(10000):
    # 计算loss
    X = train_data_X
    y = one_hot(train_data_y)
    y_hat = softmax(compute_y_hat(W,X,bias))
    loss = cross_entropy(y,y_hat)
    loss_list.append(loss)
    # 计算梯度
    grad_w = (1/len(X))*np.dot(X.T,(y_hat - y))
    grad_b = (1/len(X))*np.sum(y_hat - y)
    #更新参数
    W = W - lr*grad_w.T
    bias = bias - lr*grad_b
    #输出
    if i%300 == 1:
        print("i: %d,loss : %f"%(i,loss))

plt.plot(loss_list)

plt.scatter(c_1[:,0],c_1[:,1],marker = '+')
plt.scatter(c_0[:,0],c_0[:,1],marker = '^')
plt.scatter(c_2[:,0],c_2[:,1],marker = '*')
plt.scatter(c_3[:,0],c_3[:,1])
x = np.arange(-5,5)
y1 = -(W[0,0]*x + bias[0,0])/W[0,1]
y2 = -(W[1,0]*x + bias[0,1])/W[1,1]
y3 = -(W[2,0]*x + bias[0,2])/W[2,1]
y4 = -(W[3,0]*x + bias[0,3])/W[3,1]
plt.plot(x,y1,'b')
plt.plot(x,y2,'y')
plt.plot(x,y3,'g')
plt.plot(x,y4,'r')

def predict(x):
    y_hat = softmax(compute_y_hat(W,x,bias))
    #取one_hot编码中的最大值
    return np.argmax(y_hat,axis = 1)[:,np.newaxis]

np.sum(predict(test_data_X) == test_data_y)

2.9. 感知器

2.9.1. 感知器理论

感知器也是一个非常经典的机器学习线性模型的参数学习算法，他处理的是二分类问题：

给定大小为N的样本的训练集{(X1,y1),(X2,y2)……(Xn,yn)}，感知器的算法希望找到一组参数W，使得对于所有样本都有 y*W.T*X > 0

感知器也是一个由错误驱动的算法，因此我们也可以通过一个权重向量w，每次分错一个样本（x,y）时，可以得到yW.T*X < 0,其中y*x是小于0的，我们用y*x来更新权重：

感知器的学习过程：

损失函数：

梯度：

感知器的不足：

在数据集线性可分时，我们能找到一个超平面将两类数据分开，但并不能保证其泛化能力。
感知器对样本出现的顺序比较敏感，不同顺序找到的超平面往往也不一样。
如果训练集不是线性可分的，那就永远不会收敛。

2.9.2. 感知器（实战）

注意，感知器严格要求标签是1和-1。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)
Num = 100

# y = 1
x_1 = np.random.normal(6,1,size = (Num)) # 6附近的满足高斯分布的点
x_2 = np.random.normal(3,1,size = (Num)) # 3附近的反差为1的点
y = np.ones(Num)
c_1 = np.array([x_1,x_2,y]) #[x1,x2]是特征,y是样本的预测值。
c_1.shape

# y = -1
x_1 = np.random.normal(3,1,size = (Num)) # 6附近的满足高斯分布的点
x_2 = np.random.normal(6,1,size = (Num)) # 3附近的反差为1的点
y = np.ones(Num)*-1
c_0 = np.array([x_1,x_2,y]) #[x1,x2]是特征,y是样本的预测值。
c_0.shape

# 一般表头是特征，行是样本。
c_1 = c_1.T
c_0 = c_0.T

plt.scatter(c_1[:,0],c_1[:,1],marker = '+')
plt.scatter(c_0[:,0],c_0[:,1])

#混合
All_data = np.concatenate((c_1,c_0))
All_data.shape #(默认在行上拼接)

np.random.shuffle(All_data) #默认是在第一维度，也就是列上打乱。

np.random.shuffle(All_data)  #默认是在第一维度，也就是列上打乱。
train_data_X = All_data[:150, :2]
train_data_y = All_data[:150, -1].reshape(150,1)
test_data_X = All_data[150:, :2]
test_data_y = All_data[150:, -1].reshape(50,1)
train_data_X.shape, test_data_y.shape

W = np.zeros((2,1))
T = 10
k = 0
train_data = np.concatenate( (train_data_X,train_data_y) ,axis = 1 )

for t in range(T):
    np.random.shuffle(train_data)
    for i in range(len(train_data)):
        # 选取第 i 个样本
        pre = np.dot(W.T,( train_data[i][-1]*train_data[i][:2] ).reshape(2,1))[0,0]
        if pre <= 0:
            W = W + (train_data[i][-1]*train_data[i][:2]).reshape(2,1)

# y = w*x + w2 *x2
plt.scatter(c_1[:,0],c_1[:,1],marker = '+')
plt.scatter(c_0[:,0],c_0[:,1])
x = np.arange(10)
y = -(W[0]*x)/W[1]
plt.plot(x,y)

2.10. 用softmax回归进行MNIST数据集的手写数字识别（实战）

一个正确率为0.9009的W，也许是因为后面不小心多训练了几千次，导致有些偏执。

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import datasets

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()

x_train.shape , y_train.shape,x_test.shape,y_test.shape

plt.imshow(x_train[0]/255.,cmap='gray')

# 把数据集形状变为： (60000,784)
x_train = x_train.reshape(-1,784)
x_train.shape

np.random.seed(0)
W = np.random.rand(784,10)
bias = np.random.rand(1,10)
W,bias.shape

#计算每个类别的预测值
def softmax(z):
    exp = np.exp(z - np.max(z,axis = 1).reshape(len(z),1))
    sum_exp = np.sum(exp,axis = 1,keepdims=True)
    return exp/sum_exp

#测试
tmp = np.arange(6).reshape(2,3)
softmax(tmp)

#给标签进行one-hot编码
def one_hot(temp):
    one_list = np.zeros((len(temp),len(np.unique(temp) )))
    one_list[np.arange(len(temp)) , temp.astype(np.int).T] = 1
    return one_list

#测试
one_hot(y_train)

#就算y_hat
def compute_y_hat(W,X,b):
    return np.dot(X,W) + b

# x_train.shape,W.shape,bias.shape
compute_y_hat(W,x_train,bias)

# 定义损失函数
def cross_entropy(y,y_hat):
    return -(1/len(y))*np.sum(np.nan_to_num(y*np.log(y_hat + 1e-9)))
# 测试

#定义超参数和其他参数：
Num = 100
lr = 0.001
loss_list = []
one_hot(y_train).shape,compute_y_hat(W,x_train,bias).shape

for t in range(Num):
    X = x_train
    y = one_hot(y_train)
    y_hat = compute_y_hat(W,X,bias)
    #讲y_hat转换为概率
    y_hat = softmax(y_hat)
    loss = cross_entropy(y,y_hat)
    loss_list.append(loss)
    # 计算梯度
    grad_w = (1/len(X))*np.dot(X.T,(y_hat - y))
    grad_b = (1/len(X))*np.sum(y_hat - y)
    #更新参数
    W = W - lr*grad_w
    bias = bias - lr*grad_b
    #输出
    if t%30 == 1:
        print("i: %d,loss : %f"%(t,loss))

W

plt.plot(loss_list)

def predict(x):
    y_hat = softmax(compute_y_hat(W,x,bias))
    #取one_hot编码中的最大值
    return np.argmax(y_hat,axis = 1)[:,np.newaxis]

x_test = x_test.reshape(-1,784)

pre = predict(x_test)
np.sum(pre.T == y_test)/len(y_test)

三：前馈神经网络

3.1. 神经元与激活函数

神经元：下图有d个输入，我们可以认为当d是净输入的时候，d就是神经元的输入，让净输入加权求和并加上偏执项，并最终求和，得到一个输出，将这个输出作为激活函数的输入，其会对加权和再做一次运算最后输出a。这就是一个典型的神经元。

激活函数：对于上图右部分即激活函数，其主要作用就是加强网络的表达能力，还有学习能力。我们要求激活函数是：

1. 连续的，可以允许个别点不可导，但绝大多数都是可导的，并且是非线性的。这样的函数是可以让参数是可学习的

2. 我们还希望激活函数是尽可能简单。

3. 还希望激活函数的治愈是在一个比较小的区间内。

常用的激活函数有：

Sigmoid：是一个s型的函数，两端是饱和的，即在负无穷和正无穷的时候，导数都趋近于0
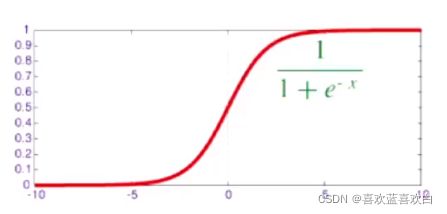
logistics：下图红色的曲线，值域在(0,1)间。可以看成一个挤压的函数，不管输入是多少，我都可以把区间挤压到(0,1)之间，当x趋近于0的时候，基本都是一个线性，导数是很明显的。可以看成是一个软性门（softGATE），控制输入的量。
tanh：黑色虚线，值域在(-1,1)之间。是0中心化的。非0中心化的输出会使得其后一层神经元的输入发生偏移，会导致收敛速度降低。

ReLU神经元：

好处：

只采用加乘的计算，使得训练过程变得简单。计算更加高效。
单侧抑制，款兴奋边界。
因为样本中往往只有较少的是有用的，而ReLU是一个稀疏的网络，只让少数神经元起作用。
在一定程度上缓解了梯度消失的问题。

坏处：因为稀疏性，也会使某些神经元死亡，不再起作用，就会误杀。因此有很多优化版本

3.2. 全连接神经网络（前馈神经网络/多层感知器）介绍

前馈神经网络：各神经元分别属于不同的层，层内无连接。而是层与层之间的连接。整个网络无反馈，信号从输入层向输出层单向传播。

他的信息是单向的，经过每层网络提取不同的特征，最终的到结果。

通用近似定理：因为前馈神经网络具有很强的拟合能力。只要至少有一个隐藏层，一些常见的连续的非线性函数都可以使用前馈神经网络近似。

将通用近似定理应用到机器学习上，神经网络就可以当做一个万能函数来使用，可以用来进行复杂的特征转换，或逼近一个复杂的条件分布。

每一个函数f都是可以进行一个特征转换，直到最后经过分类器g。最后得到我们需要的参数 $\theta$ 。他们都可以作为激活函数。中间的激活函数一般用ReLU。

3.3. 反向传播算法

先说训练参数的方法，再先就是确定损失函数。

其中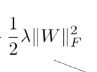是一个正则化项。是一个F范数，是用来减轻过拟合的。F范数是矩阵范数的一种，他是矩阵元素绝对值平方和再开方。

加入上图是一个神经网络，第一层有n个神经元，第二层有m层神经元。则这两层间的W有n*w个。第三个又有多少神经元……从最左到最优，所有的W就会组成一个矩阵，对于这个矩阵，我们可以用F范数作为他的正则化项。 $\lambda$ 是一个正超参数，当他越大，W越接近于0。

在定义了损失函数后，我们就可以通过梯度下降法来优化参数。

当有l层时，我们需要对每一层的W都有一个更新。

用链式法则逐一的对参数求导是很低效率的。可以采用反向传播算法来高效的实现求导。

链式法则：

反向传播也是在链式法则的基础上实现的。

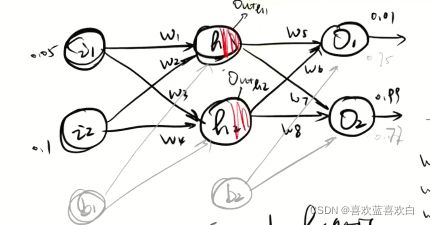
假如现在的神经网络是上图这样，当我们按照经过一层输入层，再经过隐藏层进行正向传播后，我们就可以开始反向传播了。

设总体的误差为两个神经元的和。Et = E1 + E2。分别算出两个神经元的误差后，得出总体的误差。

反向传播算法看了很多网课，我也很难了解本质。之后再总结。

3.4. 自动梯度计算

1. 在进行数值微分的时候，为了减少舍入的误差。将deta x 扩大为两倍。

2. 符号微分：先化简再求导。

3. 自动微分：利用链式法则自动计算复合函数的梯度。

比如把公式转为图的形式解释：

公式：

如果一个参数有多条路径，则要把每个路径相加。

因为输入到输出过程中，维度可能增加也可能减少，当减少时，适合反向传播，增加则适合正向传播，我们一般都是减少为维度的过程，因此一般都是用反向传播。

3.5. Himmelblau函数求极小值（实战）

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import  cm

def himmelblau(x):
    # x : [x[0],x[1]]
    return (x[0]**2 + x[1] - 11)**2 + (x[0]+x[1]**2 - 7)**2

x = np.arange(-6,6,0.1)
y = np.arange(-6,6,0.1)
x.shape,y.shape

X,Y = np.meshgrid(x,y) #形成坐标矩阵

Z = himmelblau([X,Y])
Z

fig = plt.figure('himmelblau')
ax = fig.gca(projection='3d')
ax.plot_surface(X,Y,Z)
ax.view_init(60,30)
plt.show()

# 参数初始化
x = tf.constant([4.,0.0])

lr = 0.01
for t in range(100):
    with tf.GradientTape() as tape:
        tape.watch(x)
        y = himmelblau(x)
        grads = tape.gradient(y,x)
    x = x - lr*grads
x,y

3.6. 全连接神经网络MNIST分类（实战）

建立了三层网络模型，输入层784个神经元，第一个隐藏层256个神经元，第二个隐藏层128个神经元，输出层10。标签通过one-hot编码，转变为一个向量。

权重和偏执的维度：

完整代码：

import tensorflow as tf
import matplotlib.pyplot as plt

tf.__version__

#输入层 h0 784
# w1
#隐藏层 h1 256
# w2
#隐藏层 h2 128
# w3
#输出层 h3 10

# 初始化参数
w1 = tf.Variable(tf.random.truncated_normal([784,256] , stddev = 0.1) ) #truncated_normal 有截断的正态分布
w2 = tf.Variable(tf.random.truncated_normal([256,128] , stddev = 0.1))
w3 = tf.Variable(tf.random.truncated_normal([128,10] , stddev = 0.1))

b1 = tf.Variable(tf.zeros([256]))
b2 = tf.Variable(tf.zeros([128]))
b3 = tf.Variable(tf.zeros([10]))
b1.shape

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
x_train.shape , y_train.shape , x_test.shape , y_test.shape

#x值都是0-255之间的，我们想让他先变为0到1之间。并且想数据类型为浮点数。
x_train = tf.convert_to_tensor(x_train , dtype = tf.float32)/255.
y_train = tf.convert_to_tensor(y_train,dtype=tf.int32)

# 把训练集拉平，并且转换为tensor类型。
x_train = tf.reshape( x_train ,[-1,784] )
max(x_train[0])

# h1: net(z = wx+b ) out1( ReLU(z) )
# [60000,784]@[784,256] + [256]
net1 = x_train@w1 + tf.broadcast_to(b1 , [x_train.shape[0],256])
# net1是输入层的输出，其作为输入再次进入第一个隐藏层的特征
out1 = tf.nn.relu(net1)

# [60000,256]@[256,128] + [128]
net2 = out1@w2 + b2
out2 = tf.nn.relu(net2)

# [60000,128]@[128,10] + [10]
net3 = out2@w3 + b3
out3 = tf.nn.softmax(net3)

y_train = tf.one_hot(y_train,depth=10)

loss = tf.nn.softmax_cross_entropy_with_logits(labels = y_train,logits = out3)
loss

#原本是在每个值上做了个对比，我们想求出一个平均
loss = tf.reduce_mean(loss)
loss

with tf.GradientTape() as tape:
    tape.watch([w1,b1,w2,b2,w3,b3])
    out1 = tf.nn.relu(x_train@w1 + b1)
    out2 = tf.nn.relu(out1@w2 + b2)
    out3 = tf.nn.softmax(out2@w3 + b3)
    loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels = y_train,logits = out3))
grads = tape.gradient(loss , [w1,b1,w2,b2,w3,b3])


lost_list = []

lr = 0.1

#更新参数
#w = w - lr*grads
w1.assign_sub(lr*grads[0])
b1.assign_sub(lr*grads[1])
w2.assign_sub(lr*grads[2])
b2.assign_sub(lr*grads[3])
w3.assign_sub(lr*grads[4])
b3.assign_sub(lr*grads[5])

for step in range(3000):
    with tf.GradientTape() as tape:
        tape.watch([w1,b1,w2,b2,w3,b3])
        out1 = tf.nn.relu(x_train@w1 + b1)
        out2 = tf.nn.relu(out1@w2 + b2)
        out3 = tf.nn.softmax(out2@w3 + b3)
        loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels = y_train,logits = out3))
    grads = tape.gradient(loss , [w1,b1,w2,b2,w3,b3])
    #更新梯度
    w1.assign_sub(lr*grads[0])
    b1.assign_sub(lr*grads[1])
    w2.assign_sub(lr*grads[2])
    b2.assign_sub(lr*grads[3])
    w3.assign_sub(lr*grads[4])
    b3.assign_sub(lr*grads[5])
    #输出
    lost_list.append(loss)
    if step % 100 == 1:
        print(step ,"loss: ",float(loss))

plt.plot(lost_list)

x_test = tf.convert_to_tensor(x_test , dtype=tf.float32)/255
y_test = tf.convert_to_tensor(y_test , dtype=tf.int32)

x_test  = tf.reshape(x_test , [-1,784])

out1 = tf.nn.relu(x_test@w1 + b1)
out2 = tf.nn.relu(out1@w2 + b2)
out3 = tf.nn.softmax(out2@w3 + b3)

y_predict =  tf.math.argmax(out3,axis=-1)
y_predict = tf.cast(y_test,tf.int32)

result = tf.equal(y_predict,y_test)
result = tf.cast(result , dtype=tf.int32)
true_sum = tf.reduce_sum(result)
accuracy = true_sum/len(y_test)
accuracy

最后在测试集上的正确率为 100%。注意此代码用的是批量随机梯下降法。

因此计算速度偏低

可以使用小批量随机梯度下降法

在tensorflow中有专门的batch方式

# batch_size

batchDataset = tf.data.Dataset.from_tensor_slices((x_train , y_train)).batch(128)
train_iter = iter(batchDataset)
sample = next(train_iter) #取值
sample[0].shape, sample[1].shape

四：TF2 基础（实战）

4.1. 变量与张量介绍

import tensorflow as tf

tf.__version__

# 张量 Tensor 张量其实就是一个多维数组
# 张量的维度可以是0 : 1,2,3
# dim = 0 : 1,2,3 (一组数)
# dim = 1 : [1,2,3] (向量)
# dim = 2 : [ [2,3],[4,4] ] (二维矩阵)

tf.constant(1.)

#无法进行浮点数转整数
# tf.Variable(1.,dtype=tf.int32)
#但可以整数转浮点数
tf.Variable(1 ,dtype=tf.float32)

tf.constant("hello")

tf.constant(True)

tf.constant([1,2,3,4])

tf.range(10)

a = tf.reshape(tf.range(10) , [2,5])

a.shape

aa = a.cpu()

aa.device

aa = a.gpu()

aa.device

tf.is_tensor(aa)

isinstance(aa,tf.Tensor)

a = tf.zeros([3,5])
a

b = tf.ones_like(a)
b

tf.fill([5,7],3,0)

tf.random.normal([3,5],stddev=2,mean=5)
#这样的生成随机数的值，两边趋近于0，因此容易出现梯度消失的问题

#为了解决以上问题,把某些值截断
tf.random.truncated_normal([3,5])

# 索引和切片与numpy差不多
v = tf.Variable([1,2,3,4])
v[0]

a = tf.Variable(tf.reshape(tf.range(10),[2,5]))
a

a[1,2]

# 行全选，列选取第2列
a[:,2]

4.2. 张量的计算与转换

tf.add(1,2)

tf.add([1,2],[3,4])

a = tf.Variable(5)
a**2

tf.square(5)

# 一般求均值，求和，求最大值等都会有个降维的操作
tf.reduce_sum([1,2,3])

tf.reduce_sum([[1,2,3],[4,5,6]])

tf.reduce_sum([[1,2,3],[4,5,6]] ,axis = 0)

tf.reduce_sum([[1,2,3],[4,5,6]] ,axis = 1)

a = tf.constant([[1]])
b = tf.constant([[2,3]])
tf.matmul(a,b)

a@b

#转换为numpy
a.numpy()

# 转换为张量
tf.convert_to_tensor(a)

4.3. 张量的合并与分割

t1 = tf.constant( [[1,2,3],[4,5,6]])
t2 = tf.constant( [[7,8,9],[10,11,12]])
t1,t2

tf.concat([t1,t2],axis = 1)

tf.concat([t1,t2] ,axis=0)

# 假如img1，img2是一个图片，我们想把图片叠加在一起。
img1 = tf.random.uniform([3,4])
plt.matshow(img1)
img2 = tf.random.uniform([3,4])
plt.matshow(img2)

img_stack = tf.stack([img1,img2],axis = 0)
img_stack

img_stack.shape

# 除了要合并的维度可以不同，其他维度值是相同的。
#就比如，图片的数量可以是不相同的，但是每张图片的像素点是相同的
#就是说，stack 所有的张量的形状都是相同的

# unstack
a,b = tf.unstack(img_stack,axis=0)

a,b

#拆分 把数据按维度拆分为几份
# [2,3,4]
# [60000,28,28]
a,b = tf.split(img_stack , axis=2,num_or_size_splits=[1,3])

a,b

4.4. 张量的数据统计

# 向量的范数
x = tf.ones([2,3])
x

# 1范数
tf.norm(x , ord=1)

# 在某维度上求那一维度的范数
tf.norm(x,ord=1,axis = 0)

# 无穷范数
tf.norm(x,ord=np.inf)

# 求最大值、最小值、均值、和
a = tf.reduce_min(x,axis = 0)
b = tf.reduce_mean(x,axis = 0)
a,b

#比较
a = tf.ones([5],dtype=tf.int32)
b = tf.constant([1,2,1,2,3,])
a,b

z = tf.equal(a,b)
z

# 转变数据类型
z = tf.cast(z,dtype=tf.int32)
tf.reduce_sum(z)

4.5. 张量的填充与复制

tf.pad(x,[ ]) 第二个参数[ [a1,b1], [a2,b2] ,[a3 ,b3] ] 中填的是某维度(第几个就是第几维度)，左边的参数是那个维度上，左边填充多少，如[a1,b1]意思是左边填充a1个单位，右边填充b1个单位

# 填充一般会在收/尾加0，通过填充来满足我们数据形状的要求
# padding

# I like the weather day  .
# 1  2    3     4     5   6
# so do I .
# 7  8  9 6
# 我们想把这两个句子放在同一个张量中去，形状就要一样

a = tf.constant([1,2,3,4,5,6])
b = tf.constant([7,8,1,6])

# tf.pad(x,padding)
#padding [ [],[],[] ] # 第一个中括号对就是第几维度的，中括号左边的是在那一维度上，左边填充的0，右边就是右边填充的0

b = tf.pad( b,[ [0,2] ] )
b

c = tf.stack([a,b],axis = 0)
c

# 有些句子比较长，因此我们只需要找到适合大部分句子的最大长度
# 因此有些句子要截取相应的长度。一般取80

total_words = 1e5
max_review_len = 80
embedding_len = 100

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.imdb.load_data()

len(x_train[0])

# tf.keras.preprocessing.sequence.pad_sequences 针对数据集进行操作

x_train = tf.keras.preprocessing.sequence.pad_sequences(x_train,maxlen=max_review_len,truncating='post',padding='post')
x_train.shape

# 截取，并且补0，并转变为数组
x_train

x = tf.random.truncated_normal([4,28,28])
x.shape

# 把x转变为 [32,32]
x = tf.pad(x,[[0,0],[2,2],[2,2]])

x.shape

# tf.tile() 实现长度为1的在任意维度复制功能

x = tf.random.truncated_normal([4,28,28,3])
x = tf.tile(x,[2,3,3,1])
x.shape

# [4,28,28,3],四张图片，像素点为28*28,有三个通道
x[1,:,:,1].shape

# 数据的限幅 tf.maximunm(x,a) # [a,+……]
x = tf.range(9)
x

#下限
tf.maximum(x,6)

#上限
tf.minimum(x,6)

# 另外 relu本身也是一个有限幅功能的激活函数
def relu(x):
    return tf.maximum(x,0.)

# 一起用就是一个范围
tf.minimum(tf.maximum(x,2),7)

#或者使用
tf.clip_by_value(x,2,7)

4.6. tf.gather()

tf.gather(x, []) ，第二个参数中填的是坐标，最后组成一个数组。

如：班级i ，学生j ，成绩k

tf.gather_nd(x ,[ [1,1,2] ,[2,2,3], [3,3,4] ]) 就是 [1,1,2] ,[2,2,3], [3,3,4] 对应的三个值或数组组成的另一个数组。

# 4个班级 35个人 8个科目
x = tf.random.uniform( [4,35,8],maxval=100,dtype=tf.int32 )
x

x[:2]

tf.gather(x,[0,1], axis=0)

# 所有第0维度的，第1，5，8第1维度的所有第2维度的数据
tf.gather(x,[0,4,7] ,axis=1)

# 所有班的所有同学的，第3，5门成绩
tf.gather(x,[2,4],axis=2)

# 第2，3班的第第[3，4，5，6，27]的成绩
#gather具有语义性
ban = tf.gather(x,[1,2],axis = 0)
xues = tf.gather(ban,[2,3,5,6,27],axis = 1)
xues

# 抽2班的2号，3班的3号，4班的4号
x[1,1],x[2,2],x[3,3]

tf.stack([x[1,1],x[2,2],x[3,3]],axis = 0)

# tf.gather_nd,采样多个样本，后面的是坐标
tf.gather_nd(x,[[1,1],[2,2],[3,3]])

# 班级i ，学生j ，成绩k
tf.gather_nd(x ,[ [1,1,2] ,[2,2,3], [3,3,4] ])

4.7. tf.boolean_mask()

# 班级的维度上进行采样
mask = [True ,False ,False ,True ] #mask的形状必须与想选取的样本数据的维度相等
tf.boolean_mask(x,mask,axis=0)

4.8. tf.where(cond,x,y)

        cond == True ：x 否则y

a = tf.ones([2,2])
b = tf.zeros([2,2])
a,b

cond = tf.constant([[True,False] , [False,True]])

tf.where(cond , a,b)

# 不指定x，y 只返回为真的索引
tf.where(cond)

#假如我们想知道张量中为正数的索引是哪些
x = tf.random.normal([3,3])
x

# 直接返回了为true的坐标
indices = tf.where(x>0)

#获取索引后，又可以通过gather_nd获取相应的位置，并打包
tf.gather_nd(x,indices)

4.9. scatter_nd(indices,updates,shape)

        可以高效的刷新张量的部分数据,可以根据索引，用update来更新shape

indices = tf.constant( [ [4],[3],[1],[7] ] ) # 坐标
updates = tf.constant( [1.,2.,3.,4.] ) # 对应坐标即将填充的值
tf.scatter_nd(indices , updates,[8]) # 在白板上填充值

4.10. tf.meshgrid()

# 暴力操作
points = []
for x in np.arange(-8,8,0.1):
    for y in np.arange(-8,8,0.1):
        z = x**2 + y**2
        points.append([x,y,z])
len(points)

x = tf.linspace(-8.,8.,160) # 平均分为160份
y = tf.linspace(-8.,8.,160)
x,y = tf.meshgrid(x,y)

z = x**2 + y**2

fig = plt.figure()
ax = Axes3D(fig)
ax.contour3D(x,y,z,500)
plt.show()

4.11. 数据集加载与预处理

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()

# 合并
train_db = tf.data.Dataset.from_tensor_slices( (x_train , y_train) )

# 打乱操作
train_db = train_db.shuffle(10000) #buffer_size 缓冲区大小，防止随机每次按照不一定的随机。

# 每次训练只是进行 小批量训练
#batch_size ，每一批训练的样本大小
train_db = train_db.batch(128)

# 预处理
#一开始的数据不满足我门的要求
def preprocess(x,y):
    x = tf.cast(x,dtype=tf.float32)/255.
    y = tf.one_hot(y,depth=10)
    return x,y

# 直接就是一个映射
train_db = train_db.map(preprocess)

for x,y in train_db:
    print(y)

# 一个batch 的训练 step
# 多个step完成一个epoch
# 多个epoch完成一个训练

for epoch in range(20):
    for step , (x,y) in enumerate(train_db):
        #训练
        pass

五：Keras高层接口

5.1. 模型的装配、训练和测试

import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow import keras
from tensorflow.keras import Sequential,layers

x = tf.constant([1.,2.])

# 实例化 一个softmax
softmax = keras.layers.Softmax()

softmax(x)

#直接用不能用，只能先实例化
keras.layers.Softmax(x)

# sequential,内部写，网络的输入之后考虑
network = Sequential([
    #全连接
    layers.Dense(3), # 三个神经元
    layers.ReLU(), #神经元可以写里面，也可以写在外面
    layers.Dense(2,activation=layers.ReLU())
])

x = tf.random.truncated_normal([4,3])
network(x)

# 参数还包括偏执
network.summary()

# 也可以通过add增加新的层，动态实现网络维护
model = Sequential()
model.add(layers.Dense(3))
model.add(layers.Dense(3))
model.build((None, 4)) # None指的是样本个数为任意值，4是指有多少个特征和3个神经# 元做连接
model.summary()

5.2. 模型的装配、训练与测试

# 装配
model = Sequential([
    layers.Dense(256,activation='relu'),
    layers.Dense(128,activation='relu'),
    layers.Dense(64,activation='relu'),
    layers.Dense(32,activation='relu'),
    layers.Dense(10,activation='softmax')
])

model.build(input_shape=(None,784))

model.summary()

# 确定优化器optimizer(求梯度的方式)、损失函数loss、监控指标metrics等
model.compile(
            optimizer=keras.optimizers.SGD(learning_rate=0.01),
              loss = tf.keras.losses.CategoricalCrossentropy(),
              metrics = ['accuracy']
              )

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()

def preprocess(x,y):
    x = tf.cast(x,dtype=tf.float32)/255.
    x = tf.reshape(x,[-1,784])
    y = tf.one_hot(y,depth=10)
    return x,y

# 合并
train_db = tf.data.Dataset.from_tensor_slices( (x_train , y_train) )
# 打乱操作
train_db = train_db.shuffle(10000) #buffer_size 缓冲区大小，防止随机每次按照不一定的随机。
# 每次训练只是进行 小批量训练
# batch_size ，每一批训练的样本大小
train_db = train_db.batch(128)
# 预处理
#一开始的数据不满足我门的要求
# 直接就是一个映射
train_db = train_db.map(preprocess)

model.fit(train_db,epochs=10

# 合并
test_db = tf.data.Dataset.from_tensor_slices( (x_test , y_test) )
# 打乱操作
test_db = test_db.shuffle(10000) #buffer_size 缓冲区大小，防止随机每次按照不一定的随机。
# 每次训练只是进行 小批量训练
# batch_size ，每一批训练的样本大小
test_db = test_db.batch(128)
# 预处理
#一开始的数据不满足我门的要求
# 直接就是一个映射
test_db = test_db.map(preprocess)

model.predict(test_db)

model.evaluate(test_db)

5.3. 模型的保存和加载

!dir
# 以张量的形式保存
model.save_weights('weight.ckpt') #以此保存是最轻量级的，并没有保存模型的结构

!dir

# 删除模型
del model

# 装配
model = Sequential([
    layers.Dense(256,activation='relu'),
    layers.Dense(128,activation='relu'),
    layers.Dense(64,activation='relu'),
    layers.Dense(32,activation='relu'),
    layers.Dense(10,activation='softmax')
])

# 确定优化器optimizer(求梯度的方式)、损失函数loss、监控指标metrics等
model.compile(
            optimizer=keras.optimizers.SGD(learning_rate=0.01),
              loss = tf.keras.losses.CategoricalCrossentropy(),
              metrics = ['accuracy']
              )

model.load_weights('weight.ckpt')

model.evaluate(test_db)

model.save('model.h5')

!dir

del model

model = keras.models.load_model('model.h5')

model.evaluate(test_db)

# 部署在实际中，具有平台的无惯性
tf.compat.v1.keras.experimental.export_saved_model(model,'save_model')

!dir

del model

model = tf.compat.v1.keras.experimental.load_from_saved_model('save_model')

# 这样读取的还是一个sequential
model

# 我们还需要把compile加进来
# 确定优化器optimizer(求梯度的方式)、损失函数loss、监控指标metrics等
model.compile(
            optimizer=keras.optimizers.SGD(learning_rate=0.01),
              loss = tf.keras.losses.CategoricalCrossentropy(),
              metrics = ['accuracy']
              )

model.evaluate(test_db)

5.4. 自定义网络层类

继承tf.keras.layers.Layer 类，并重写init、 build 、和call三个方法

__init__ ，可以在其中执行所有与输入无关的初始化
build，你可以在其中了解输入张量的形状，并可以执行其余的初始化
call，在这里进行正向计算

import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow import keras
from tensorflow.keras import Sequential,layers

tf.test.is_gpu_available()

class MyDense_relu(tf.keras.layers.Layer):
    # 自定义的全连接层
    def __init__(self,units):
        super().__init__()
        self.units = units

    def build(self, input_shape):
        self.w = self.add_variable(name='w',
                                   shape=[input_shape[-1],self.units],#第一个维度是输入的最后形状最后一个数，即特征个数，第二个维度是网络神经元个数
                                   initializer = tf.initializers.RandomNormal() #初始化
                                   )
        self.b = self.add_variable(name='b',
                                   shape=[self.units],
                                   initializer = tf.initializers.Zeros())

    def call(self, inputs, **kwargs):
        # w*x + b
        # w [input_shape[-1] ,units]
        # x [50000]
        return tf.nn.relu(inputs @self.w + self.b)

class MyDense_softmax(tf.keras.layers.Layer):
    # 自定义的全连接层
    def __init__(self,units):
        super().__init__()
        self.units = units

    def build(self, input_shape):
        self.w = self.add_variable(name='w',
                                   shape=[input_shape[-1],self.units],#第一个维度是输入的最后形状最后一个数，即特征个数，第二个维度是网络神经元个数
                                   initializer = tf.initializers.RandomNormal() #初始化
                                   )
        self.b = self.add_variable(name='b',
                                   shape=[self.units],
                                   initializer = tf.initializers.Zeros())

    def call(self, inputs, **kwargs):
        # w*x + b
        # w [input_shape[-1] ,units]
        # x [50000]
        return tf.nn.softmax(inputs @self.w + self.b)

class MyMdoel(keras.Model):
    def __init__(self):
        super().__init__()
        self.fc1 = MyDense_relu(512)
        self.fc2 = MyDense_relu(256)
        self.fc3 = MyDense_relu(128)
        self.fc4 = MyDense_softmax(10)

    def call(self,inputs):
        fc1w_out = self.fc1(inputs)
        fc2w_out = self.fc2(fc1w_out)
        fc3w_out = self.fc3(fc2w_out)
        fc4w_out = self.fc4(fc3w_out)
        return fc4w_out

myModel = MyMdoel()
myModel.build(input_shape=(None,784))
myModel.summary()

myModel.compile(optimizer=keras.optimizers.SGD(),
                loss=keras.losses.CategoricalCrossentropy(),
                metrics=['accuracy'])

def preprocess(x,y):
    x = tf.cast(x,dtype=tf.float32)/255.
    x = tf.reshape(x,[-1,784])
    y = tf.one_hot(y,depth=10)
    return x,y

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
# 合并
train_db = tf.data.Dataset.from_tensor_slices( (x_train , y_train) )
# 打乱操作
train_db = train_db.shuffle(10000) #buffer_size 缓冲区大小，防止随机每次按照不一定的随机。
# 每次训练只是进行 小批量训练
# batch_size ，每一批训练的样本大小
train_db = train_db.batch(128)
# 预处理
#一开始的数据不满足我门的要求
# 直接就是一个映射
train_db = train_db.map(preprocess)

# 合并
test_db = tf.data.Dataset.from_tensor_slices( (x_test , y_test) )
# 打乱操作
test_db = test_db.shuffle(10000) #buffer_size 缓冲区大小，防止随机每次按照不一定的随机。
# 每次训练只是进行 小批量训练
# batch_size ，每一批训练的样本大小
test_db = test_db.batch(128)
# 预处理
#一开始的数据不满足我门的要求
# 直接就是一个映射
test_db = test_db.map(preprocess)

myModel.fit(train_db,epochs=10)

myModel.evaluate(test_db)

5.5. 测量工具和可视化

新建测量器->写入数据->读入统计数据->清零测量器

import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow import keras
import numpy as np
from tensorflow.keras import Sequential,layers
tf.test.is_gpu_available()

# y_hat[0,1,1]
# y [0,1,2]

# 新建测量器
m= keras.metrics.Accuracy() #适用于实值
# 写入数据
m.update_state([0,1,1],[0,1,2])
# 读取统计信息
m.result()

#不清除的话，若是循环，肯定会在新建那里出问题
m.reset_states()

m.result()

# y_hat[0,1,1]
# y [0,1,2]

# 新建测量器
m= keras.metrics.CategoricalAccuracy()
# 写入数据
m.update_state([ [0,0,1] ,[0,1,0]],[ [0.1,0.9,0.8], [0.05,0.95,0]] )
# 读取统计信息
m.result()


#不清除的话，若是循环，肯定会在新建那里出问题
m.reset_states()

acc_meter = keras.metrics.Accuracy()
loss_meter = tf.keras.metrics.Mean()

# 装配
model = Sequential([
    layers.Dense(256,activation='relu'),
    layers.Dense(128,activation='relu'),
    layers.Dense(64,activation='relu'),
    layers.Dense(32,activation='relu'),
    layers.Dense(10,activation='softmax')
])

model.build(input_shape=(None,784))
model.compile(optimizer=keras.optimizers.SGD(),
                loss=keras.losses.CategoricalCrossentropy(),
                metrics=['CategoricalAccuracy'])

def preprocess(x,y):
    x = tf.cast(x,dtype=tf.float32)/255.
    x = tf.reshape(x,[-1,784])
    y = tf.one_hot(y,depth=10)
    return x,y
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
# 合并
train_db = tf.data.Dataset.from_tensor_slices( (x_train , y_train) )
# 打乱操作
train_db = train_db.shuffle(10000) #buffer_size 缓冲区大小，防止随机每次按照不一定的随机。
# 每次训练只是进行 小批量训练
# batch_size ，每一批训练的样本大小
train_db = train_db.batch(128)
# 预处理
#一开始的数据不满足我门的要求
# 直接就是一个映射
train_db = train_db.map(preprocess)
# 合并
test_db = tf.data.Dataset.from_tensor_slices( (x_test , y_test) )
# 打乱操作
test_db = test_db.shuffle(10000) #buffer_size 缓冲区大小，防止随机每次按照不一定的随机。
# 每次训练只是进行 小批量训练
# batch_size ，每一批训练的样本大小
test_db = test_db.batch(128)
# 预处理
#一开始的数据不满足我门的要求
# 直接就是一个映射
test_db = test_db.map(preprocess)

op = tf.optimizers.Adam(0.01)

for epoch in range(5):
    for step, (x,y) in enumerate(train_db):
        with tf.GradientTape() as tape:
            loss = tf.losses.categorical_crossentropy(y,model(x))
            loss_meter.update_state(loss)
        grads = tape.gradient(loss,model.trainable_variables)
        op.apply_gradients(zip(grads,model.trainable_variables))
        if step % 100 == 1:
            print("epoch: ",epoch ,'step' , step ,'loss' ,loss_meter.result().numpy())
        loss_meter.update_state(loss)

    for step, (x,y) in enumerate(test_db):
        out = model(x)
        pred = tf.cast(tf.argmax(out,axis = -1) , dtype = tf.int32)
        y = tf.cast(tf.argmax(y,axis = -1) , dtype = tf.int32)
        acc_meter.update_state(y,pred)
    print('epoch:' , epoch , 'acc:' ,acc_meter.result().numpy())
    acc_meter.reset_states()

六：卷积神经网络

6.1. 全连接神经网络存在的问题

权重矩阵的参数非常多

有较高的内存占用，依赖硬件。

我们通常取I层中对J层中j点影响最大的前k个点作为集合去计算。

因此我们需要知道第I层节点对第J层节点影响大小分布。

为了解决这个问题，我们一般都会引入一些先验知识

位置近与否？

以一个中心点到之外的窗口宽的位置，我们认为他很重要，这个区域成为感受野

上述总的中心点在输出中设为j，感受野是输入中的关于j的一块小区域。

2. 时间近与否？

除了上述讲的感受野的局部相关性的思想，我们还可以通过权值共享的思想减少参数。网络部分区域始终使用一个参数。

局部不变形的特征

自然图像中的物体都具有局部不变性的特征，比如尺寸缩放、平移、旋转等操作不影响其语义信息。

而全连接网络很难提取这些局部不变特征。

6.2. 卷积是什么？

两函数的卷积、本质上就是先将一个函数翻转、然后进行滑动叠加。

1D连续卷积：连续形式，相当于积分求面积。离散时相当于求所有点值的和。

g(t) 是一个响应信号，f(t)是个输入信号。输出与输入信号与响应的程度相关。如下图，响应程度越来越小，即使输入信号有时很大，但最后还是会对输入影响越来越小。

在1D中的翻转可以理解为响应信号的翻转。

接下来是滑动。

而叠加，就是上面说的“ 1D连续卷积：连续形式，相当于积分求面积。离散时相当于求所有点值的和。”

6.2.1. 1D卷积

现在我们假设信号发生器每个时刻t产生一个信号xt，其信号衰减率为wk（上述说的g(t) ），即在k-1个时间步长后，信息为原来的wk倍。（假设W1 = 1，W2 = 1/2 ， w3 = 1/4）

时刻t收到的信号yt为当前产生的信息和以前时刻延迟信息的叠加。这也是离散的卷积，其中wk也被称为滤波器（或卷积核）。

信号序列x和滤波器w，卷积的输出为：

举一个1D卷积的例子：

输入：

卷积核：[-1,0,1]

卷积过程：翻转滑动求和

则第一步：翻转卷积核 [1,0,-1]

输入序列分别与卷积三三相乘并求和（第3步）。假设滑动（第二步）步长为1的情况小，得出输出序列 [-1,2,1,1,0]

6.2.2. 2D卷积

图像处理中，图像是以二维矩阵的形式输入到神经网络中，因此，我们需要二维卷积。

步长为1的情况下，先将卷积核翻转，再进行以下这样的滑动，滑动完就进行求和。

卷积常备作为特征的提取器。

计算卷积时还需要进行翻转操作，但卷积的目标是：提取特征，因此往往翻转是不必要的，这样的卷积操作被称为互相关操作，除非特别声明，卷积一般是指“互相关”的。

6.2.3. 卷积扩展-步长和填充

这里的步长s和零填充p都是针对滤波器的。

步长是指：滤波器滑动时的时间间隔或越过数量。

步长越大，输出形状就越小。

填充的作用是什么呢？如果我们经过卷积计算后，输出过小，我们想维持特征的数量，这时就要对卷积核进行0填充。

输出的大小可以通过一个公式算出：其中n为输入矩阵（n*n），m是卷积核（m*m），p是0填充数，s是步长。

$\frac{n - m + 2p}{s} + 1$

因此卷积核的大小，我们要设定好，保持输出为整数。且通过公式我们又进一步得出，步长越大，输出形状越小。

回到0补充，为了保持特征的数量，我们一般可以通过计算得出正确的补0数。

6.3. 通道与卷积核

综上我们可以通过卷积层代替全连接层解决权重矩阵参数过过多的问题。

6.3.1. 单通道-单卷积核

单通道是对于黑白照片而言的，他矩阵中的每一个值都是一个标量，表示像素点。

6.3.2. 多通道-单卷积核

一张彩色图片一个像素点有3个通道。输入图片有三个通道，那么我们的卷积核也应该有对于的三个通道。即卷积的通道数与输入通道数一致！

每个通道都与对应的权重矩阵滑动，求和，最后再进行一个权重向量的求和。

但是单卷积核只能适用于对某一特点的特征提取的作用，但往往图片也不可能只有一个特征，因此我们最常用的是多通道-多卷积核的操作。

6.3.3. 多通道-多卷积核

一个卷积核，虽然有多个通道，但是最后使用求和方式让权重叠加，这仍是一个特征。而两个卷积核可以提取两个特征，最后将两个个特征stack，这样就代表两个特征。多个卷积核同理。

6.4. 卷积运算（实战）

6.4.1. 卷积计算

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
tf.test.is_gpu_available()
import matplotlib.pyplot as plt

# batch_shape + [in_height, in_width, in_channels]
#定义输入
x = tf.random.normal([1,5,5,3])
x

plt.imshow(x[0])

# 定义卷积核
# [filter_height, filter_width, in_channels, out_channels]
w = tf.random.normal([3,3,3,6]) # 6个卷积核在做运算。最后得出6个特征。

out1 = tf.nn.conv2d(x,w,[1,1],[[0, 0], [0, 0], [0, 0], [0, 0]])
# 步长 ：1（水平，竖直都移动这个数） ， 2（分别代表水平竖直）， 4个数
# padding: ‘SAME’输入和输出都是同样大小的。自动在四周补0（直接等于一个字符串）padding = 'SAME',
# 而VALID操作则是不够的地方直接抛弃，不再计算边缘。就是和不补0是一样的结果
out1

out2 = tf.nn.conv2d(x,w,[1,1],'SAME')
out2

# 而VALID操作则是不够的地方直接抛弃，不再计算边缘。就是和不补0是一样的结果
out3 = tf.nn.conv2d(x,w,[1,1],'VALID')
out3

# 与卷积计算不一样的是，卷积层不用设置卷积的权值张量和偏执，他会自动设置这些。
cnnlayer = layers.Conv2D(filters=4,kernel_size=3) #kernel_size 是指卷积核的宽度,并不是通道数。

x

out = cnnlayer(x)
out

6.5. 池化层

直观上也会进行一个特征选择，从而降低特征的数量，从而进一步降低参数的数量，除此之外，他还解决全连接前馈网络不具备空间不变性的问题。

通过卷积层得到的特征数据不具备空间不变性（空间不变性如下图，位置，大小，亮度等），只有通过池化层才能具备空间不变形的特征。

池化层可以理解为对图像进行一个下采样的过程，对于每一次滑动窗口内的所有值，输出其中的最大值，均值或其他方法产生的值，而不再是像卷积中一样全部乘后求和。

我们从上图也可以看出经过池化层后特征映射空间也能在很大幅度上减小特征空间，在减小特征空间后又有一个很直接的好处，那就是减少过拟合。

同时还能增加下一次的kernel感受野。

池化也有一个很严重的问题：

我们的采样区如果对于图片过大的时候，那么带来的直接的结果就是造成信息损失。

6.6. 卷积网络结构

卷积网络是由卷积层。池化层、全连接层交叉堆叠而成：

而上面的这个结构肯能也会由多个组成，最后再加上一个全连接层。

卷积趋向于小卷积、大深度。全卷积、少池化的趋势发展。

表示学习：

我们总说层数越深，网络的表达能力就越强，那怎么样才能表示能力强呢？于是人们提出了反卷积神经网络使得可视化出特征映射到底是什么样的情况。因此图片学习也是一个表示学习的过程，先提取颜色特征再提取边缘特征再提取高阶的特征……

6.7. 梯度计算

卷积的反向传播是怎样进行的呢？

假设我们有一张图片（3*3），卷积核（2*2）。s = 1,p = 0时，通过点积运算得到一个输出。再利用这个输出与真实值比较得到一个loss从而进行反向传播得到梯度，再来进行梯度更新。

6.8. LeNet-5（实战）

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
tf.test.is_gpu_available()

batch = 32

model = tf.keras.Sequential([
    layers.Conv2D(6,3),#卷积核的数量是6，卷积核的大小是3*3
    layers.MaxPool2D(pool_size=2,strides=2),#最大值池化层
    keras.layers.ReLU(),
    layers.Conv2D(16,3),#卷积核的数量是16，卷积核的大小是3*3
    layers.MaxPool2D(pool_size=2,strides=2),#最大值池化层
    layers.ReLU(),
    layers.Flatten(),#把原来权重矩阵拉平，方便做全连接层
    layers.Dense(120,activation='relu'),
    layers.Dense(84,activation='relu'),
    layers.Dense(10,activation='softmax')
])

model.build(input_shape=(batch,28,28,1))

model.summary()

model.compile(
    optimizer=keras.optimizers.Adam(),
    loss = keras.losses.CategoricalCrossentropy(),
    metrics=['accuracy']
)

def preprocess(x,y):
    x = tf.cast(x,dtype=tf.float32)/255.
    x = tf.reshape(x,[-1,28,28,1])
    y = tf.one_hot(y,depth=10)
    return x,y
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
# 合并
train_db = tf.data.Dataset.from_tensor_slices( (x_train , y_train) )
# 打乱操作
train_db = train_db.shuffle(10000) #buffer_size 缓冲区大小，防止随机每次按照不一定的随机。
# 每次训练只是进行 小批量训练
# batch_size ，每一批训练的样本大小
train_db = train_db.batch(128)
# 预处理
#一开始的数据不满足我门的要求
# 直接就是一个映射
train_db = train_db.map(preprocess)
# 合并
test_db = tf.data.Dataset.from_tensor_slices( (x_test , y_test) )
# 打乱操作
test_db = test_db.shuffle(10000) #buffer_size 缓冲区大小，防止随机每次按照不一定的随机。
# 每次训练只是进行 小批量训练
# batch_size ，每一批训练的样本大小
test_db = test_db.batch(128)
# 预处理
#一开始的数据不满足我门的要求
# 直接就是一个映射
test_db = test_db.map(preprocess)

model.fit(train_db,epochs=5)

model.evaluate(test_db)

6.9. AlexNet -------第一个现代深度卷积网络模型（理论+实战）

创新点：

使用多GPU进行并行训练
使用了ReLu作为非线性激活函数
使用Dropout防止过拟合

由下图可以看出，Dropout会使一部分神经元在作用时消失。

Dropout具体工作流程：

先随机的删除网络中的一般半的隐藏神经元，输入输出的神经元保持不变。
然后把输入x通过修改后的网络向前传播，然后把得到的损失值通过修改后的网络进行反向传播。一小批样本执行玩这个过程后，在没有被删除的神经元上按照随机梯度下降法更新对应的（w,b）
然后重复这一过程：恢复被删除的神经元，再随机删掉，再通过删掉部分隐藏神经元后的样本进行训练，得到的输出仍保持不变。即删除的神经元只在训练时体现被删除。

使用数据增强技术

因为神经网络训练的参数多，表达能力强。因此我们需要比较多的数据量，不然容易造成过拟合。当训练数据有限时，可以通过一些变换从已有的数据集中产生新的数据。对于图像而言，我们可以进行一些形变（翻转，随机裁剪，平移，颜色光照变换）操作。

此外，AlexNet还进行了主成分分析。

层叠池化

在LeNet中池化是不重叠的，即吃化的窗口的大小和步长相等的。

而在AlexNet中使用的池化确实可以重叠的，也就是说，在池化的时候，每次移动的步长小于池化窗口的长度，这样就有部分的重叠，重叠池化有个好处就是抑制过拟合。

局部响应归一化（LRN）

LRN是仿造生物学上，活跃的神经元会对相邻的神经元造成抑制现象，好处是：

归一化有助于快速收敛‘；

对局部神经元活动创建一个竞争机制，使得其中响应较大的值变得更大，并抑制其他反馈较小的神经元，增强了模型的泛化能力；

局部响应突出的是待归一化的点，之和相同通道上附近的点，做相乘求和加偏执再次方等运算。

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
tf.test.is_gpu_available()

x = tf.random.normal([1,227,227,3])
x

#对于x这张图片
#第一层:卷积
c1_c = layers.Conv2D(filters=96,kernel_size=11,strides=4)
out1 = c1_c(x)
out1

#第二层 relu
relu = layers.ReLU()
out2 = relu(out1)
out2

# 第三层：MaxPooling
mp = layers.MaxPool2D(pool_size = (3,3) , strides=2)
out3 = mp(out2)
out3

#第四层：局部归一化
out4 = tf.nn.local_response_normalization(out3,5,2,0.0001,0.75)
out4

class c2(layers.Layer):
    def __init__(self):
        super().__init__()

    def build(self, input_shape):
        self.w = tf.random.normal([5,5,input_shape[-1] ,256])

    def call(self, inputs, **kwargs):
        return tf.nn.conv2d(inputs,filters=self.w,strides=1,padding = [[0, 0], [2, 2], [2, 2], [0, 0]])

## 卷积核的数量有点像特征的数量。

x = tf.random.normal([1,227,227,3])

alexNet = keras.Sequential([
    #第一大层
    layers.Conv2D(96,11,4),
    layers.ReLU(),
    layers.MaxPool2D((3,3),2),
    layers.BatchNormalization(),

    #第二大层
    c2(),
    layers.ReLU(),
    layers.MaxPool2D((3,3),2),
    layers.BatchNormalization(),

    #第三大层
    layers.Conv2D(384,3,1,padding='SAME'),
    layers.ReLU(),

    #第四大层
    layers.Conv2D(384,3,1,padding='SAME'),
    layers.ReLU(),

    #第五大层
    layers.Conv2D(256,3,1,padding='SAME'),
    layers.ReLU(),
    layers.MaxPool2D((3,3),2),

    #第六层
    layers.Flatten(),
    layers.Dense(4096),
    layers.ReLU(),
    layers.Dropout(0.25),

    #第七层
    layers.Flatten(),
    layers.Dense(4096),
    layers.ReLU(),
    layers.Dropout(0.25),

    layers.Dense(1000),
    layers.Softmax()
])

alexNet(x).shape

alexNet.build(input_shape=([None,227,227,3]))
alexNet.summary()

# 读取数据
# alexNet.compile()
# alexNet.fit(train_db,epochs=5)

6.10. BN （理论+实战）

BN层：batch normalization

为什么要有normalization（归一化）

为了解决全连接神经网络参数过多，我们选用了卷积，卷积可以减少参数，增加网络的深度。但是越深的网络就越对超参数敏感，即超参数小的变化可能就会对网络训练轨迹有很大的影响。

为了解决这个问题，有人就设计出来一个参数标准化的准则。

而BN层也是这种标准化，他可以让网络超参初始化能够更加的随意、自由。切网络的收敛速度会更快，性能也会更好。此后卷积层，BN层，ReLu层，池化层一度成为网络结构的标配。

那么第一层的输出作为第二层输入的时候，标准化操作具体的好处呢？

之前我们在做MNIST数据集手写数字识别的时候，开始做了一个归一化的操作，即把所有数除以255，让所有数全部在0到1之间，这样有什么好处呢？

1. 网络学习的本质：输入数据的一个分布，一旦训练数据和测试数据分布不同，泛化能力就不同。所以我们在选择样本的时候都要满足独立同分布。

2. 如果分布不同的话，网络收敛速度也会降低。

3. 输入的图片可能只是光照不同，可是读数据的时候，差别可能会很远，但事实上他们是一个东西。

在模型里面为什么要做归一化呢？

模型训练后，训练的参数就会发生变化，比如W，W变化的时候，下一层输入也会发生相应变化，这种现象叫做ICS。这种偏移现象我们也不希望发生，所以希望在输入到下一层的时候，我们也希望它能够标准化。

如上图，梯度趋近与0和趋近于正无穷的地方，通过标准化，让x趋近于0和正无穷的数趋近于0，也就是让样本几乎都在这中间。这样就减轻了梯度弥散的现象。

再举个例子，现有两个输入，y = x1*w1 + x2*w2，

当两个输入分布相同时（如右图），它能够很好的逐步找到最优值，但是当分布不同时（如左图），他很曲折的才能走到最优值。

总结就是，希望分布较小，且接近。

如何进行标准化呢？

我们可以在输入的时候直接加一个预处理，比如，我们希望均值为0，方差为1.

原本经过ReLu小于0的样本会被截断，但是在进行一般标准化后，有部分样本又会小于0，因此又要经过一些变化（如下图），乘以的是缩放/放大，加的数是平移，如刚讲的我们希望大于0的话，让样本往右适当平移即可，有其他需求就进行相应的变换即可。

训练过程是：1.先计算均值，和方差。再根据上图公式，计算BN层的输入。同时按照下图更新方式，更新全局统计值均值和方差。

测试过程是： 直接计算并输出x_test。

之后还要进行一个反向传播。

BN存在的问题：

如果下图中，batchSize设置的过小的话，或者样本数据本来就很少，那么那些数据并不能代表整体的分布，但是太大的话，硬件又不能支持训练所需的条件。

为了解决BN的这个问题，有人又提出了GN层（Group Normalization）。

下图红色曲线是GN，其在batch_size逐渐增大的时候，错误率任然很稳定。而BN（下图蓝线）却在逐步上升。

H、W是高宽，C是通道数，N是batch坐标轴，如下图知，BN是在做batch上的归一化（N*H*W）.Layer Norm 是在channel上做归一化（C*H*W），Instance Norm统计每个样本每个通道上的均值和方差（H*W）。GN在channel上做了一个分组，在每个组上做归一化（G*H*W）。因此GN就与batch是没有关系的。

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
tf.test.is_gpu_available()

# 构造BN层输入

# [b,h,w,c]
x = tf.random.normal([100,32,32,3])

x = tf.reshape(x,[-1,3])

#第一步，计算三个通道上的均值μ
tf.reduce_mean(x,axis = 0)

model = keras.Sequential([
    layers.Conv2D(6,3),
    layers.BatchNormalization(),
    layers.ReLU(),
    layers.MaxPool2D()
])

out1 = model(x)
model.variables

out2 = model(x,training=False)
model.variables

6.11. VGG （理论+实战）

VGG的改进：

1. 显著增加了网络层数（16到19）

2. 大大减小了Kernnel size，全部使用3*3的CONV stride 1 padding 1的卷积核，相对于AAlexNet中的11*11、5*5、3*3的卷积核，参数量更小，计算代价更低。

3. 采用了更小的池化层：2*2的窗口，步长为2。不过AlexNet的池化层好处就是池化窗口宽度大于步长，因此是个叠加的池化层。

VGG的优点：

1. VGGNet的结构非常简洁，整个网络都使用了同样大小的卷积核尺寸（3*3）和最大池化尺寸（2*2）

2. 几个小滤波器（3*3）卷积层的组合比一个大滤波器（5*5）卷积层要好。

3. 验证了可以通过不断加深网络的结构来提升性能。

VGG的缺点：

耗费资源多，全连接层有较多参数。

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import datasets, layers , optimizers , models , regularizers
import numpy as np
import matplotlib.pyplot as plt
tf.__version__

# 零均值归一化
def normalize(X_train,X_test):
    #归到0到1之间
    X_train = X_train / 255.
    X_test = X_test / 255.

    mean = np.mean(X_train,axis=(0,1,2,3))
    std = np.std(X_train , axis=(0,1,2,3))
    print("mean: ",mean ,"std: ",std)

    # 0均值标准化
    X_train = (X_train - mean) / (std + 1e-7)
    X_test = (X_test - mean) / (std + 1e-7) #注意均值方差用的都是训练集的。

    return X_train,X_test

#读入数据
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data()
(x_train.shape, y_train.shape), (x_test.shape, y_test.shape)

#归一化数据
x_train,x_test = normalize(x_train,x_test)

def preprocess(x ,y):
    x = tf.cast(x,tf.float32)
    y = tf.cast(y,tf.int32)
    y = tf.squeeze(y,axis = 1)
    y = tf.one_hot(y,depth=10)
    return x,y

train_db = tf.data.Dataset.from_tensor_slices((x_train,y_train))
train_db = train_db.shuffle(50000).batch(128).map(preprocess)

test_db = tf.data.Dataset.from_tensor_slices((x_test,y_test))
test_db = train_db.shuffle(50000).batch(128).map(preprocess)

# VGG 16
num_classes = 10 #当前分类有10类,VGG16是1000,的数据集

model = keras.Sequential()

model.add(layers.Conv2D(64 , (3,3) ,padding='same', activation='relu'))
model.add(layers.Conv2D(64 , (3,3) ,padding='same', activation='relu'))
model.add(layers.MaxPool2D(pool_size=(2,2) , strides=2)) #参数高宽减半

model.add(layers.Conv2D(128 , (3,3) ,padding='same', activation='relu'))
model.add(layers.Conv2D(128 , (3,3) ,padding='same', activation='relu'))
model.add(layers.MaxPool2D(pool_size=(2,2) , strides=2)) #参数高宽减半

model.add(layers.Conv2D(256 , (3,3) ,padding='same', activation='relu'))
model.add(layers.Conv2D(256 , (3,3) ,padding='same', activation='relu'))
model.add(layers.Conv2D(256 , (3,3) ,padding='same', activation='relu'))
model.add(layers.MaxPool2D(pool_size=(2,2) , strides=2)) #参数高宽减半

model.add(layers.Conv2D(512 , (3,3) ,padding='same', activation='relu'))
model.add(layers.Conv2D(512 , (3,3) ,padding='same', activation='relu'))
model.add(layers.Conv2D(512 , (3,3) ,padding='same', activation='relu'))
model.add(layers.MaxPool2D(pool_size=(2,2) , strides=2)) #参数高宽减半

model.add(layers.Conv2D(512 , (3,3) ,padding='same', activation='relu'))
model.add(layers.Conv2D(512 , (3,3) ,padding='same', activation='relu'))
model.add(layers.Conv2D(512 , (3,3) ,padding='same', activation='relu'))
model.add(layers.MaxPool2D(pool_size=(2,2) , strides=2)) #参数高宽减半

model.add(layers.Flatten())
model.add(layers.Dense(256 , activation='relu')) # VGG 16为4096,但是这里没有必要，因为其实输入的像素点也不是那么多
model.add(layers.Dense(128 , activation='relu')) # VGG 16为4096,
model.add(layers.Dense(num_classes,activation='softmax'))

model.build(input_shape = (None,32,32,3))

model.summary()

model.compile(optimizer=optimizers.Adam(0.0001),
              loss=keras.losses.CategoricalCrossentropy(from_logits=True),# API上说加上from_logits=True这句话可能可以得到更好的结果
              metrics=['accuracy']
              )

history = model.fit(train_db,epochs=50) #用history可以得到一些监控指标

import matplotlib.pyplot as plt

plt.plot(history.history['loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()

model.evaluate(test_db)

我们可以通过最后得到的loss知道，训练到还没到一半，他的loss逐步上升，开始朝着不好的方向训练，那原因是什么呢？可能是学习率比较大。初始化等多种原因。

我们一般可以：

1. 调低学习率。

2. 调整参数的初始化方法。

3. 调整输入数据的标准化方法

4. 修改loss函数

5. 增加正则化

6.使用BN/GN层（中间层数据的标准化）（可以不受学习率的影响）

7.使用dropout

改进版本：

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import datasets, layers , optimizers , models , regularizers
import numpy as np
import matplotlib.pyplot as plt
tf.__version__

# 零均值归一化
def normalize(X_train,X_test):
    #归到0到1之间
    X_train = X_train / 255.
    X_test = X_test / 255.

    mean = np.mean(X_train,axis=(0,1,2,3))
    std = np.std(X_train , axis=(0,1,2,3))
    print("mean: ",mean ,"std: ",std)

    # 0均值标准化
    X_train = (X_train - mean) / (std + 1e-7)
    X_test = (X_test - mean) / (std + 1e-7) #注意均值方差用的都是训练集的。

    return X_train,X_test

#读入数据
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data()
(x_train.shape, y_train.shape), (x_test.shape, y_test.shape)

#归一化数据
x_train,x_test = normalize(x_train,x_test)

def preprocess(x ,y):
    x = tf.cast(x,tf.float32)
    y = tf.cast(y,tf.int32)
    y = tf.squeeze(y,axis = 1)
    y = tf.one_hot(y,depth=10)
    return x,y

train_db = tf.data.Dataset.from_tensor_slices((x_train,y_train))
train_db = train_db.shuffle(50000).batch(128).map(preprocess)

test_db = tf.data.Dataset.from_tensor_slices((x_test,y_test))
test_db = test_db.shuffle(50000).batch(128).map(preprocess)

# VGG 16
num_classes = 10 #当前分类有10类,VGG16是1000,的数据集
weight_decay =  0.000
model = keras.Sequential()

model.add(layers.Conv2D(64 , (3,3),padding='same',kernel_regularizer=regularizers.l2(weight_decay)))
model.add(layers.Activation('relu'))
model.add(layers.BatchNormalization())
model.add(layers.Dropout(0.3))

model.add(layers.Conv2D(64 , (3,3) ,padding='same',kernel_regularizer=regularizers.l2(weight_decay)))
model.add(layers.Activation('relu'))
model.add(layers.BatchNormalization())

model.add(layers.MaxPool2D(pool_size=(2,2) , strides=2)) #参数高宽减半

model.add(layers.Conv2D(128 , (3,3) ,padding='same', kernel_regularizer=regularizers.l2(weight_decay)))
model.add(layers.Activation('relu'))
model.add(layers.BatchNormalization())
model.add(layers.Dropout(0.4))

model.add(layers.Conv2D(128 , (3,3) ,padding='same', kernel_regularizer=regularizers.l2(weight_decay)))
model.add(layers.Activation('relu'))
model.add(layers.BatchNormalization())

model.add(layers.MaxPool2D(pool_size=(2,2) , strides=2)) #参数高宽减半

model.add(layers.Conv2D(256 , (3,3) ,padding='same', kernel_regularizer=regularizers.l2(weight_decay)))
model.add(layers.Activation('relu'))
model.add(layers.BatchNormalization())
model.add(layers.Dropout(0.4))
model.add(layers.Conv2D(256 , (3,3) ,padding='same', kernel_regularizer=regularizers.l2(weight_decay)))
model.add(layers.Activation('relu'))
model.add(layers.BatchNormalization())
model.add(layers.Dropout(0.4))
model.add(layers.Conv2D(256 , (3,3) ,padding='same', kernel_regularizer=regularizers.l2(weight_decay)))
model.add(layers.Activation('relu'))
model.add(layers.BatchNormalization())

model.add(layers.MaxPool2D(pool_size=(2,2) , strides=2)) #参数高宽减半

model.add(layers.Conv2D(512 , (3,3) ,padding='same', kernel_regularizer=regularizers.l2(weight_decay)))
model.add(layers.Activation('relu'))
model.add(layers.BatchNormalization())
model.add(layers.Dropout(0.4))
model.add(layers.Conv2D(512 , (3,3) ,padding='same',kernel_regularizer=regularizers.l2(weight_decay)))
model.add(layers.Activation('relu'))
model.add(layers.BatchNormalization())
model.add(layers.Dropout(0.4))
model.add(layers.Conv2D(512 , (3,3) ,padding='same', kernel_regularizer=regularizers.l2(weight_decay)))
model.add(layers.Activation('relu'))
model.add(layers.BatchNormalization())

model.add(layers.MaxPool2D(pool_size=(2,2) , strides=2)) #参数高宽减半

model.add(layers.Conv2D(512 , (3,3) ,padding='same', kernel_regularizer=regularizers.l2(weight_decay)))
model.add(layers.Activation('relu'))
model.add(layers.BatchNormalization())
model.add(layers.Dropout(0.4))
model.add(layers.Conv2D(512 , (3,3) ,padding='same',kernel_regularizer=regularizers.l2(weight_decay)))
model.add(layers.Activation('relu'))
model.add(layers.BatchNormalization())
model.add(layers.Dropout(0.4))
model.add(layers.Conv2D(512 , (3,3) ,padding='same', kernel_regularizer=regularizers.l2(weight_decay)))
model.add(layers.Activation('relu'))
model.add(layers.BatchNormalization())

model.add(layers.MaxPool2D(pool_size=(2,2) , strides=2)) #参数高宽减半

model.add(layers.Flatten())
model.add(layers.Dense(512 , kernel_regularizer=regularizers.l2(weight_decay)))
model.add(layers.Activation('relu'))
model.add(layers.BatchNormalization())

model.add(layers.Dropout(0.5))
model.add(layers.Dense(num_classes,activation='softmax'))

model.build(input_shape = (None,32,32,3))

model.summary()

model.compile(optimizer=optimizers.Adam(0.0001),
              loss=keras.losses.CategoricalCrossentropy(from_logits=True),# API上说加上from_logits=True这句话可能可以得到更好的结果
              metrics=['accuracy']
              )
history = model.fit(train_db,epochs=50) #用history可以得到一些监控指标

import matplotlib.pyplot as plt

plt.plot(history.history['loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()

model.evaluate(test_db)

50次epoch后，loss仍然在下降。结果还可以更好

loss收敛图：

6.12. GoogleNet（理论+实战）

GoogleNet也是一个有很高的的深度的模型，但是他的参数量（500完）却比AlexNet以及VGG要小很多。VGG大概是GoogleNet的3倍。

GoogleNet是怎样进一步提高神经网络的性能的呢？首先来看深度网络结构存在的问题：

1. 增加深度（增加层数），增加宽度（增加神经元的数量），可以提高网络性能，但是会带来而更多的参数，如果训练数据集是有限的，就很容易造成一个过拟合。

2. 网络过大、参数过多，计算复杂度大，难以应用

3. 网络越深，容易出现梯度弥散的问题（梯度往后越容易消失），难以优化模型。

有没有一种办法既能优化网络，又能提高性能计算呢？

能不能把全连接变成稀疏连接呢？其实无论是稠密矩阵，还是稀疏矩阵他在做相乘的时候，各地方的数字都是会相乘，那我们能不能利用稀疏矩阵的稀疏性，来直观地增大计算时间呢？

已经有人证明，把稀疏矩阵聚集成一个密集的矩阵，是能够进行增加计算的性能。

GoogleNet提出了Inception基本结构

如何设计卷积核的大小是一个很重要的问题，在Inception结构中，一个卷积层包含多个不同大小的卷及操作，称为Inception模块。

Inception模块可以同时使用不同大小的卷积核，并将得到的特征映射在深度上堆叠起来作为输出的特征映射。当然即使是不同的卷积核，我们也希望结果大小是一样的，因此会使用一个‘SAME’的操作。

通过设计一个稀疏的网络结构，但是又能产生稠密的数据，因此满足了加强网络表现，又保证计算资源的使用效率。

原始的Inception基本结构中5*5的卷积核会造成输出厚度过大，为了避免这样的情况。我们可以在3*3，5*5之前，maxpooling之后分别加上1*1的卷积核，以降低特征图的厚度。

而GoogleNet就是用多个Inception模块和少量汇聚层堆叠。

V2版本中，发现，5*5的参数量是3*3的接近3倍，于是就提出，用两层3*3的卷积层来替代5*5。之后又想能不能用更小的卷积核呢？于是就考虑了n*1的网络。

import os
import tensorflow as tf
import numpy as np
from tensorflow import keras
tf.__version__

# 零均值归一化
def normalize(X_train,X_test):
    #归到0到1之间
    X_train = X_train / 255.
    X_test = X_test / 255.

    mean = np.mean(X_train,axis=(0,1,2,3))
    std = np.std(X_train , axis=(0,1,2,3))
    print("mean: ",mean ,"std: ",std)

    # 0均值标准化
    X_train = (X_train - mean) / (std + 1e-7)
    X_test = (X_test - mean) / (std + 1e-7) #注意均值方差用的都是训练集的。
    return X_train,X_test

def preprocess(x ,y):
    x = tf.cast(x,tf.float32)
    y = tf.cast(y,tf.int32)
    y = tf.squeeze(y,axis = 1)
    y = tf.one_hot(y,depth=10)
    return x,y

#读入数据
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data()
(x_train.shape, y_train.shape), (x_test.shape, y_test.shape)

#归一化数据
x_train,x_test = normalize(x_train,x_test)

train_db = tf.data.Dataset.from_tensor_slices((x_train,y_train))
train_db = train_db.shuffle(50000).batch(128).map(preprocess)

test_db = tf.data.Dataset.from_tensor_slices((x_test,y_test))
test_db = test_db.shuffle(50000).batch(128).map(preprocess)

class ConvBNRelu(keras.Model):
    # Conv + BN + ReLu,加了一个BN层
    def __init__(self,filters,kernelSize=3,strides=1,padding='same'):
        super().__init__()

        self.model = keras.models.Sequential([
            keras.layers.Conv2D(filters=filters,
                                kernel_size=kernelSize,
                                strides=strides,
                                padding=padding
                                ),
            keras.layers.BatchNormalization(),
            keras.layers.ReLU()
        ])

    def call(self,x,training=None):
        x =self.model(x,training=training)
        return x

# 注意这里的卷积 和 池化 是并行的

class Inception_v2(keras.Model):
    # 构造Inception_v2模块
    def __init__(self , filters , strides = 1):
        # strides 控制是否缩减特征图，=1 不缩减， =2 ，缩减
        super().__init__()

        self.conv1_1 = ConvBNRelu(filters , kernelSize=1,strides=1)
        self.conv1_2 = ConvBNRelu(filters , kernelSize=3,strides=1)
        self.conv1_3 = ConvBNRelu(filters , kernelSize=3,strides=strides)

        self.conv2_1 = ConvBNRelu(filters , kernelSize=1,strides=1)
        self.conv2_2 = ConvBNRelu(filters , kernelSize=3,strides=strides)

        self.pool = keras.layers.MaxPooling2D(pool_size=3,
                                              strides=strides,
                                              padding='SAME')

    def call(self, inputs, training=None):
        x1_1 = self.conv1_1(inputs,training=training)
        x1_2 = self.conv1_2(x1_1,training=training)
        x1_3 = self.conv1_3(x1_2,training=training)

        x2_1 = self.conv2_1(inputs , training=training)
        x2_2 = self.conv2_2(x2_1,training = training)

        x3 = self.pool(inputs)

        # 在最后一个，即通道维度上
        x = tf.concat([x1_3,x2_2,x3],axis = 3)

        return x

class GoogleNet(keras.Model):

    def __init__(self , num_blocks,num_classes,filters = 16):
        # 构造GoogleNet模型
        # num_blocks：包含具有相同filter的n个Inception_v2模块的模块数

        super().__init__()

        self.filters = filters
        self.conv1 = ConvBNRelu(filters)

        self.blocks = keras.models.Sequential()

        for block_id in range(num_blocks):
            for Inception_id in range(2): #每个block里有2个Inception，也可以设置变量
                if Inception_id == 0:
                    block = Inception_v2(self.filters , strides=2) #缩放
                else:
                    block = Inception_v2(self.filters , strides=1) #不缩放
                self.blocks.add(block)

            #下一层的block中的卷积数量闭上一层的卷积核多一倍
            self.filters *= 2

        self.avg_pool = keras.layers.GlobalAvgPool2D()
        self.fc = keras.layers.Dense(num_classes,activation='softmax')

    def call(self , x , training = None):
        out = self.conv1(x , training=training)
        out = self.blocks(out , training=training)
        out = self.avg_pool(out)
        out = self.fc(out)
        return out

model = GoogleNet(2,10)
model.build(input_shape=(None , 32,32,3))
model.summary()

model.compile(optimizer=keras.optimizers.Adam(0.0001),
              loss=keras.losses.CategoricalCrossentropy(from_logits=True),# API上说加上from_logits=True这句话可能可以得到更好的结果
              metrics=['accuracy']
              )

history = model.fit(train_db,epochs=50) #用history可以得到一些监控指标

import matplotlib.pyplot as plt

plt.plot(history.history['loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()

model.evaluate(test_db)

Loss收敛图：

6.13. ResNet（实战）

上面一直在讲，深度越大，网络表达能力越强，但是深度越大，有什么坏处吗？

会带来梯度消失的问题。

解决办法：残差网络：

通过在非线性的卷积层上增加直连边的方式提高星系传播效率，在另一个方向上直接越过当前网络。值就是一个跨层链接的重要思想。

将目标函数分为两个部分：

import os
import tensorflow as tf
import numpy as np
from tensorflow import keras
tf.__version__

# 零均值归一化
def normalize(X_train,X_test):
    #归到0到1之间
    X_train = X_train / 255.
    X_test = X_test / 255.

    mean = np.mean(X_train,axis=(0,1,2,3))
    std = np.std(X_train , axis=(0,1,2,3))
    print("mean: ",mean ,"std: ",std)

    # 0均值标准化
    X_train = (X_train - mean) / (std + 1e-7)
    X_test = (X_test - mean) / (std + 1e-7) #注意均值方差用的都是训练集的。
    return X_train,X_test

def preprocess(x ,y):
    x = tf.cast(x,tf.float32)
    y = tf.cast(y,tf.int32)
    y = tf.squeeze(y,axis = 1)
    y = tf.one_hot(y,depth=10)
    return x,y

#读入数据
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data()
(x_train.shape, y_train.shape), (x_test.shape, y_test.shape)

#归一化数据
x_train,x_test = normalize(x_train,x_test)

train_db = tf.data.Dataset.from_tensor_slices((x_train,y_train))
train_db = train_db.shuffle(50000).batch(128).map(preprocess)

test_db = tf.data.Dataset.from_tensor_slices((x_test,y_test))
test_db = test_db.shuffle(50000).batch(128).map(preprocess)

#第一个s=2，后面的都为1
class ResnetBlock(keras.Model):
    def __init__(self , filters , kernelsize = 3 , strides = 1,padding = 'same'):
        super().__init__()

        self.conv_model = keras.models.Sequential([
            # 第一个卷积层
            keras.layers.Conv2D(filters=filters,
                                kernel_size=kernelsize,
                                strides=strides,
                                padding=padding),
            keras.layers.BatchNormalization(),
            keras.layers.ReLU(),
            # 第2个卷积层
            keras.layers.Conv2D(filters=filters,
                                kernel_size=kernelsize,
                                strides=1,
                                padding=padding),
            keras.layers.BatchNormalization()
        ])
        if strides != 1:
            # 即f（x）和 x形状不同的时候就要构建identity让后面相加的时候保持形状相同。
            self.identity = keras.models.Sequential([
                keras.layers.Conv2D(filters=filters,
                                    kernel_size=1,
                                    strides=strides,
                                    padding=padding
                                    ),
            ])
        else:
            # 保持原样输出
            self.identity = lambda x:x

    def call(self , inputs,training=None):
        conv_out = self.conv_model(inputs)
        identity_out = self.identity(inputs)
        out = conv_out + identity_out
        out =tf.nn.relu(out)
        return out

class ResNet(keras.Model):
    def __init__(self,block_list,num_classes):
        # block_list: 卷积核的个数和block的数量 eg. [ [64,3],[128,4] ]
        super().__init__()

        self.conv__initial = keras.layers.Conv2D(16,5,1,padding='same')
        self.blocks = keras.models.Sequential()

        # build all the blocks
        for block_id in range(len(block_list)):
            for layer_id in range(block_list[block_id][1]):
                if layer_id == 0:
                    # 每个方块中的第一个conv的stride = 2
                    self.blocks.add(ResnetBlock(filters=block_list[block_id][0],strides=2))
                else:
                    # 其他conv的stride = 1
                    self.blocks.add(ResnetBlock(filters=block_list[block_id][0],strides=1))
        self.final_bn = keras.layers.BatchNormalization()
        self.avg_pool = keras.layers.GlobalAvgPool2D()
        self.fc = keras.layers.Dense(num_classes)

    def call(self,inputs,training=None):
        out = self.conv__initial(inputs)
        out = self.blocks(out , training=training)
        out = self.final_bn(out , training = training)
        out =tf.nn.relu(out)
        out = self.avg_pool(out)
        out = self.fc(out)

        return out

num_classes = 10
batch_size = 32
epochs = 10

model = ResNet([ [64,2] , [128,3] , [256, 4] ] , num_classes)
model.compile(optimizer=keras.optimizers.Adam(0.001),
                loss = keras.losses.CategoricalCrossentropy(from_logits=True),
                metrics = ['accuracy'])

model.build(input_shape=(None , 32,32,3))
model.summary()

history = model.fit(train_db,epochs=10) #用history可以得到一些监控指标

import matplotlib.pyplot as plt

plt.plot(history.history['loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()

model.evaluate(test_db)

Loss收敛图：

在训练集上正确率高达0.97，但是在测试集上，却只有0.77的正确率。

6.14. 卷积的变种、应用、总结

其他的卷积种类：

转置卷积：低纬特征映射到高位特征，一般用在DCGAN，可以逐层放大特征图。

空洞卷积：直接增大感受野。却也增加了特征数，参数量也随之增加。因此可以使用空洞卷积，感受野变大了，但是取得值任然是3*3的。

CNN总结：

演化历史：

卷积应用：

图像识别，目标检测，图像分割，OCR，图像生成，对抗样本。

七：循环神经网络

7.1. Embedding

以前讲的都是常用与空间性的学习，而时序性的学习则需要使用循环神经网络。

那项声音，文字等序列是如何表示的呢？

可以利用序列的相关性表示。

这就可以讲到一个Embedding了。

Embeddin层：

通过计算相似度，在空间中查找最近邻。
实现高纬稀疏特征向量像低稠密特征向量的转换。
训练好的embedding可以当作输入深度学习模型的特征。

常用Embedding方式：

Word2vec（使用最为广泛的词嵌入方法）：速度快，效果好，容易扩展，简单。

一般Word2vec分为两个模型：

CBOW

1. 输入层：上下文单词的onehot。（要训练此的上下文）
所欲的onehot分别乘以共享的输入权重矩阵W
所有的向量相加求平均作为隐层向量
乘以输出权重矩阵W
得到向量经过激活函数处理得到概率分布
概率最大的index所指示的单词为预测的中间词（target word）与true label的onehot作比较，误差越小越好（更具误差更新权重矩阵）
假设我们此时的到的概率分布已经达到了设定的迭代次数，那么输入层的每个单词与矩阵W相乘得到的向量的就是我们想要的词向量。

TF实战实例：

注意：输入进去的不是真的字，而是是一个索引！！！

import tensorflow as tf
from tensorflow import keras

x = tf.range(5)
x

x = tf.random.shuffle(x)
x

net = tf.keras.layers.Embedding(input_dim=5,output_dim=4)
# input_dim 输入单词的个数 是可处理的容量，要大于真正的输入，这次实验是>5
# output_dim 是一个向量有多少个数表示。我理解为特征。

net(x)

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.imdb.load_data()

(x_train.shape, y_train.shape), (x_test.shape, y_test.shape)

tf.keras.datasets.imdb.get_word_index()

#Embedding 输入必须是等长的。因此要对数据做一些处理。
x = tf.keras.preprocessing.sequence.pad_sequences(x_train , maxlen=250)
len(x[0]),len(x_train[0])

net = tf.keras.layers.Embedding(input_dim=90000,output_dim=4)

net(x) # 25000个句子，一个句子250个单词，一个单词由4个词向量组成

情感分析，具体演示循环神经网络过程：

把序列通过数字输入，经过Embedding层转为词向量，词向量是[句子数，单词长度，词向量长度（特征）] 。

7.2. RNN介绍

首先思考这样的二分类全连接神经网络可行吗？

没一个单词对应的词向量经过一个网络层，最后再经过一个合并，然后最后再进行一个类别的区分。可这样的话，和以前的相同的，参数量也会过多。同事每个句子也没法保证每个句子的长度保一样。这样构建的全连接网络层是动态变化的。是不太好的。而且每个输入之间是没有关系的。比如x1只会和x1有关系，但是一个句子是一句话，他们之间是有关系的，我们不能捕捉这种关系。因此我们要逐一解决这种问题。

解决思路：

以前在卷积就提出过，权值共享的思路，既能减少网络的参数量，但是这一段话的句子还是将句子分开几个部分理解，还是不能理解句子的整体特征。

7.2.1. memory机制

那么怎么获取网络的整体语义信息呢？或者说怎么将特征逐渐积累，直至最后提取整个句子的信息呢？我们提出了memory机制。

如果说，网络提供一个单独的网络特征词向量，我们每次提取网络的词向量特征的时候，同时刷新memory，直到序列的最后。

将memory机制实现成一个状态张量h：

除了每个词都有一个句子的共享权值w_xh，还有一个w_hh是一个额外增加的权重。

最后一个h就能够很好的代替整个句子的语义信息。

基于上述的过程，有人提出了这样一个网络层：

在每一个时间戳上都进行一个输入输出的循环计算，在每个时间戳上，网路都会接受一个输入xt(词向量),输入网络的xt会与上一个网络的输出ht-1，计算得到该网络的输出，简要公式是：

$h(t) = f_{\Theta }(h_{t-1},x_{t})$

其中f是一个网络逻辑， $\Theta$ 是一个参数集合。

这样的网络模型，我们既可以保留之前句子的信息，也能有当前词的信息。

一个基本的CNN是：激活函数里面的，就是CNN的网络逻辑。

模型简化：

7.3. SimpleRNN （实战）

先介绍梯度的计算：

上图模型最后得到的O，可以与真实值进行比较，然后得到一个loss，然后对loss进行反向传播求得梯度，再对参数进行更新。不过循环神经网络一个很大的问题就是，我们求得的梯度过程中要进行一个Whh的连乘计算，计算起来比较慢。

SimpleRNNCell：

SimpleRNNCell是指只完成了一个时间戳上的计算（因为每个时间戳都有一个输出，这个输出与h有关），而SimpleRNN是一整个CNN过程。

输入的形状是什么呢？总共的训练集是：[多少句话,句子单词数,每个词的Embedding后的词向量长度]，训练是在句子每个单词序列上展开的，则输入的是：[句子单词数，embedding后的特征]。

那么每次运算后我们希望能够降维，只要利用 [b,f] @ [f,n]，设置n大小即可。

CNN还可以纵向进行多层训练。因为out也是一个输出，把out作为新层的输入即可。

具体计算方式既可以先纵向，再横向。当然也可以先横向再纵向。

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers

cell = layers.SimpleRNNCell(3) # 输出的个数，即n
cell.build(input_shape=(None,4)) #4是输入的，3是输出神经元的个数
cell.trainable_variables

# 【4，3】是输出有四句话，每句话被Embedding到3个词向量长度。
# 【3，3】是当前的whh,是一个额外的向量。

h_0 = [tf.zeros([4,64])] # 4个句子，做计算后姜维的到64个词向量大小
x = tf.random.normal([4,80,100]) # 4句话，每句话80个单词，100个Embedding后的大小。

# 沿着80展开，让【4,100】 @ 【100,64】
x_1 = x[:,0,:] #第一个词
x_1.shape

cell = layers.SimpleRNNCell(64)
#两个输出，一个out，一个h，h还要进入下一层进行计算。
out_1,h_1 = cell(x_1,h_0)
#这里两者完全相等
out_1==h_1

out_1.shape

h = h_0
for x_i in tf.unstack(x,axis=1):
    out , h = cell(x_i , h)

out

x_1 = x[:,0,:]

cell_0 = layers.SimpleRNNCell(64)
cell_1 = layers.SimpleRNNCell(32)

h_0 = [tf.zeros([4,64])] #把他转换为一个列表
h_1 = [tf.zeros([4,32])]

for x_i in tf.unstack(x,axis = 1): # 再s上扩展
    out_0 ,h_0 = cell_0(x_i,h_0)
    out_1 ,h_1 = cell_1(out_0,h_1)

out_1

layer = layers.SimpleRNN(64)

out = layer(x)
out

model = keras.Sequential([
    #return_sequences=True，除了最末层以外，每个时间戳伤都要返回一个状态的输出
    layers.SimpleRNN(64,return_sequences=True),
    layers.SimpleRNN(32)
])

model(x)

7.4. 循环神经网络的问题

当层数过多的时候，RNN的长期依赖问题：梯度爆炸和梯度弥散（消失）

上述梯度中有一个连乘计算，当Whh的最大特征值大于1时，就会出现梯度爆炸（因为指数级的计算是很庞大的）。而Wt 与等于 Wt-1时就会出现梯度弥散现象

使用权重衰减或梯度截断（裁剪）解决

权重衰减是通过给参数增加l1范数或l2范数的正则来限制参数的取值范围，从而使得γ <= 1，

梯度截断是另一种有效的启发式方法，当梯度的模大于一定阈值时，就将他截断成为一个较小的数。

如下图这种情况，如果不进行截断，会一下子上去，因此要在之前就要进行截断。

除了以上提到的梯度爆炸问题，梯度消失问题是循环神经网络的最主要的问题。RNN最大的问题就是，当层数增多时，之前的记忆会逐渐模糊！！！即短时记忆。除了改变学习率，减小层数，等方法外，最直接的方法就是改变学习的模型

解决方案：让过去得输出不仅作为输入，还要作为输出的一部分保留信息。

改进模型1：乘法保持信息。但是梯度爆炸的速度就更加快了。一般都会有限制，使用也只用于控制。
改进模型2：加法保持信息。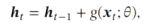会丢失非线性激活的性质，降低模型表达能力。所以我们可以把ht-1放进g（）中，即改进3.
改进模型3：增加非线性关系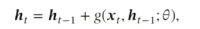：即存在线性关系，又是非线性关系。所以可以缓解改进2的丢失非线性激活的性质，但仍然存在梯度爆炸问题以及记忆容量问题。

因为每次记忆都会储存，则会出现即已饱和现象。随着时间，ht会越来越大，但是机器能存储的记忆容量是有限的，则越来越多时，也会出现记忆丢失现象。

为了解决这两个问题，我们可以引入门控这一个概念。

7.5. LSTM

相比传统的CNN来说，LSTM更擅长于处理长时间的记忆。

LSTM的原理：

与RNN的区别：

1. 除了输入的xt和ht-1之外，还加入了一个长时记忆单元c，而h控制的是一个短时的记忆。

2. 还有门控机制：输入门、遗忘门、输出门，通过三个门来控制信息的流转。

门控机制：

输出有多少取决于门控值！我们称门控程度为：门控值，其可以控制阈值。首先把门控值压缩到（0，1）之间，当sigmoid输出为0时是完全关闭，1时是完全打开。

输入门： 刷新Memory

控制LSTM对输入的接收程度，不全接收所有输入。

ht-1是之前记住的20个单词，xt表示新的10个单词。经过tanh将这两个输入做了一个融合（或者说对输入做一个非线性变换，提取所有的输入的信息，最后输出）。tanh还可以把值都压缩至（-1,1）之间。有点像归一化。而 $\sigma$ 值是阀门，可以用sigmoid产生（0,1）之间的值。

遗忘门：

Ht-1相当于短时记忆，Ct-1相当于长时记忆。遗忘门来决定长时记忆能记住多少。记住多少也是取决于ht-1和xt。而以前的记忆到底能记住记住多少个，就要看遗忘门。

当前的输出，能全部输出吗？这要看输出门。

输出门：

ct-1是直接输入，但是输入ht-1与xt则与输入门差不多，是部分输入。

输入门	遗忘门	LSTM行为
0	1	只能记忆
1	1	综合输入和记忆
0	0	清除记忆
1	0	输入覆盖记忆

LSTM变形：

1. 没有遗忘门

2. 耦合输入门和遗忘门：输入门和遗忘门，有一定的相同功能，同时使用两个门会有些冗余，于是可以将两者耦合

3.peephole连接：把长时的记忆也放进RNN中。

7.6. LSTM层在情感分类（实战）

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.imdb.load_data()
(x_train.shape, y_train.shape), (x_test.shape, y_test.shape)

# 我们希望每个输入的长度都是相同的
x_train = keras.preprocessing.sequence.pad_sequences(x_train,maxlen=250)
x_test = keras.preprocessing.sequence.pad_sequences(x_test,maxlen=250)

# 整合成一个train_db，和test_db
train_db = tf.data.Dataset.from_tensor_slices((x_train,y_train))
test_db = tf.data.Dataset.from_tensor_slices((x_test,y_test))

train_db = train_db.shuffle(10000).batch(128 , drop_remainder=True) # drop_remainder多余的就不要了
test_db = test_db.shuffle(10000).batch(128 , drop_remainder=True)

class myLSTM(keras.Model):
    def __init__(self):
        super().__init__()
        #可以吧两个输入整个作为一个输入
        self.state_0 = [tf.zeros([128,64]) , tf.zeros([128,64])]
        self.state_1 = [tf.zeros([128,32]) , tf.zeros([128,32])]

        self.embedding = layers.Embedding(input_dim=100000,output_dim=100)

        self.lstm_cell_0 = layers.LSTMCell(64)
        self.lstm_cell_1 = layers.LSTMCell(32)

        self.fc = layers.Dense(1)

    def __call__(self,inputs, *args, **kwargs):
        x = self.embedding(inputs)
        state_0 = self.state_0
        state_1 = self.state_1
        for x in tf.unstack(x,axis = 1):
            out_0 , state_0 = self.lstm_cell_0(x,state_0)
            out_1 , state_1 = self.lstm_cell_1(out_0,state_1)
        x = self.fc(out_1)
        x = tf.sigmoid(x)

        return x

model = myLSTM()
model.compile(
    optimizer=keras.optimizers.Adam(0.001),
    loss=keras.losses.BinaryCrossentropy(from_logits=True),
    metrics=['accuracy']
)

history = model.fit(train_db,epochs=10)

import matplotlib.pyplot as plt

plt.plot(history.history['loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()

model.evaluate(test_db)

也可以直接写在一个LSTM中：

class myLSTM(keras.Model):
    def __init__(self):
        super().__init__()
        self.embedding = layers.Embedding(input_dim=100000,output_dim=100)
        self.lstm_0= layers.LSTM(64 ,return_sequences=True) #与RNN同理除了最后一个前面所有都需要一个return
        self.lstm_1 = layers.LSTM(32)
        self.fc = layers.Dense(1)

    def call(self,inputs):
        x = self.embedding(inputs)
        x = self.lstm_0(x)
        x = self.lstm_0(x)
        x = self.fc(x)
        x = tf.sigmoid(x)

        return x

LOSS收敛图：

测试机上的正确率：

7.7. GRU （理论+实战）

前面说了，LSTM主要是为了解决梯度弥散的问题，但是其有个缺点就是计算复杂。

三个门复杂，参数量大。如何进行优化呢？

经过一些研究发现，遗忘门在LSTM中是最重要的一个门，这个已经在2018年的论文中得到证实，甚至发现只有遗忘门在多个数据集上能有良好的表现，甚至有些数据集上只有遗忘门的网络更优于3个门都有的网络。

在很多简化版LSTM中GRU门控循环网络是引用最广泛的LSTM变种。

GRU把状态向量，输出向量做出了一个合并。统一成为一个向量h，且把门控减少到2

复位门（重置门）：控制上一个时间戳的状态ht-1进入GRU网络的一个量。他不再像LSTM中用2个输入c和h，这里只有一个输入h。

至于上一时段的记忆通过什么来控住阈值呢？还是g作为门控。至于Wr和br只是对记忆h和输入的信息做一个特征提取。然后上一个记忆ht-1经过门控g的控制，再与当前信息x作为输入经过Wr和br的特征提取，最后经过一个激活函数tanh即可。

更新门：控制上一个时间戳上的记忆ht-1和新的ht_hat。

首先对上一个记忆ht-1和当前信息进行特征提取，并经过一个sigmoid，g这里也是阀门。ht-1经过的阀门与ht_hat加起来为1，即此消彼长，二者相互竞争的关系，最后流向ht。

具体代码：

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.imdb.load_data()
(x_train.shape, y_train.shape), (x_test.shape, y_test.shape)

# 我们希望每个输入的长度都是相同的
x_train = keras.preprocessing.sequence.pad_sequences(x_train,maxlen=250)
x_test = keras.preprocessing.sequence.pad_sequences(x_test,maxlen=250)

# 整合成一个train_db，和test_db
train_db = tf.data.Dataset.from_tensor_slices((x_train,y_train))
test_db = tf.data.Dataset.from_tensor_slices((x_test,y_test))

train_db = train_db.shuffle(10000).batch(128 , drop_remainder=True) # drop_remainder多余的就不要了
test_db = test_db.shuffle(10000).batch(128 , drop_remainder=True)

class myGRU(keras.Model):
    def __init__(self):
        super().__init__()
        #可以吧两个输入整个作为一个输入
        self.state_0 = [tf.zeros([128,64])]
        self.state_1 = [tf.zeros([128,32])]

        self.embedding = layers.Embedding(input_dim=100000,output_dim=100)

        self.gru_cell_0 = layers.GRUCell(64)
        self.gru_cell_1 = layers.GRUCell(32)

        self.fc = layers.Dense(1)

    def call(self,inputs):
        x = self.embedding(inputs)
        state_0 = self.state_0
        state_1 = self.state_1
        for x in tf.unstack(x,axis = 1):
            out_0 , state_0 = self.gru_cell_0(x,state_0)
            out_1 , state_1 = self.gru_cell_1(out_0,state_1)
        x = self.fc(out_1)
        x = tf.sigmoid(x)

        return x

model = myGRU()
model.compile(
    optimizer=keras.optimizers.Adam(0.001),
    loss=keras.losses.BinaryCrossentropy(from_logits=True),
    metrics=['accuracy']
)

history = model.fit(train_db,epochs=10)

import matplotlib.pyplot as plt

plt.plot(history.history['loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()

model.evaluate(test_db)

class myGRU(keras.Model):
    def __init__(self):
        super().__init__()
        self.embedding = layers.Embedding(input_dim=100000,output_dim=100)
        self.gru_0= layers.GRU(64 ,return_sequences=True) #与RNN同理除了最后一个前面所有都需要一个return
        self.gru_1 = layers.GRU(32)
        self.fc = layers.Dense(1)

    def call(self,inputs):
        x = self.embedding(inputs)
        x = self.gru_0(x)
        x = self.gru_1(x)
        x = self.Drop(x)
        x = self.fc(x)
        x = tf.sigmoid(x)

        return x

# 为了防止过拟合
可以加入Dropout
# 为了防止梯度爆炸
可以加入正则化项

class myGRU(keras.Model):
    def __init__(self):
        super().__init__()
        self.embedding = layers.Embedding(input_dim=100000,output_dim=100)

        self.gru_0= layers.GRU(64 ,return_sequences=True) #与RNN同理除了最后一个前面所有都需要一个return
        self.gru_1 = layers.GRU(32)

        self.bn = layers.BatchNormalization()
        self.Drop = layers.Dropout(0.5)
        self.fc = layers.Dense(1)

    def call(self,inputs):
        x = self.embedding(inputs)
        x = self.gru_0(x)
        x = self.gru_1(x)
        x = self.Drop(x)
        x = self.fc(x)
        x = tf.sigmoid(x)

        return x

model = myGRU()
model.compile(
    optimizer=keras.optimizers.Adam(0.001),
    loss=keras.losses.BinaryCrossentropy(from_logits=True),
    metrics=['accuracy']
)

history = model.fit(train_db,epochs=10)

Loss1:

训练集和测试集上的准确率：0.943，0.8345。

改进后Loss2（没有加入正则项，因为发现加入正则项无法收敛）：

训练集和测试集上的准确率：0.9529，0.8516 （10个epoch）0.9732，0.8598（20个epoch）0.9605，0.8397（学习率=0.0004，再训练10次）

7.8. 深层循环神经网络

之前说过CNN由于梯度爆炸和梯度弥散，很难进行深层训练。而LSTM主要就是用来解决梯度弥散，至于梯度爆炸可以用梯度截断的方式。

因为GRU（LSTM的改版）解决了梯度弥散的问题，于是循环神经网络就可以变得更加深层。

深层循环神经网络有以下几种形式：

堆叠循环神经网络：就是之前的纵向计算，之前是堆叠了两层。当然还可以继续堆叠。
双向循环神经网络：顺序方向和逆序方向分别训练，后进行纵向叠加。

应用场景：

RNN的特点：引入记忆，但是长程依赖问题，或是记忆容量问题，很难深层。

八：无监督学习

在现实应用中，机器学习的难点在于数据的标签难以获取。有时我们称这个工作为：数据标注工作。那有没有办法让机器来学习到数据本身的分布，是有的，我们称之为无监督学习。

无监督学习是指从无标签的数据中学习出一些有用的模式，即只有x。

无监督学习一般分为：

无监督特征学习：一般用来降维，数据可视化，或是数据预处理。
密度估计：根据一组样本来估计样本空间的概率密度。
聚类：将一组训练样本，根据不同的规则划分至不同的组里面。

8.1. 无监督特征学习

主要可分为：PCA、稀疏编码、自编码。

8.1.1. PCA （主成分分析）

是一种最常用的数据降维操作，使得在转换后的空间中的数据方差最大。假如现有一大堆东西其有很多成分构成，有些成分特别重要，有些则不。而我们需要做的工作就是把最重要的挖掘出来，所谓的降维就是将重要的特征取出来，然后特征的降低，即可以达到维度的降低。把高位数据集映射到低位空间中。

PCA一般会用来做数据预处理，但是PCA并不能一定提高模型的准确性，因为在降维的时候，就已经有一定的信息丢失。即通过降维提高准确性是不很可靠的。

因此PCA只是用在那种准确率本来就已经很高，我们可以使用PCA来实现模型的简化复杂度。对于太复杂的模型，PCA就可以实现即简单准确率又高。

那么我们是怎么将 N维向量降到R维，并且保留大部分的信息呢？

找到一条直线，使得两个特征的点在线上的产生映射，最后从二维降到一维。这条线的选取标准就是想让所有的点在线上的映射会足够的分散，即方差足够的大。

其他维度都是类似的。先找第一个方向方差最大，之后找第二个方差最大。我们希望每个维度的信息相关性足够小，甚至完全不相关。即正交！

协方差可以表示两个维度的相关性，当协方差为0的时候就是正交，我们就说此时两变量是完全不相关的。

总结就是在每个维度内，我们都希望方差是最大的（即点足够分散），但是维度之间，我们希望协方差为0（即特征之间尽可能没有关系）。即我们要找到R个正交基。同时每个维度方差足够大。

如M*M -> N*M我们希望每行间的协方差=0，行内方差最大。

用这样一个矩阵来表示各行之间协方差的关系：

假设有一个原始矩阵：有一个X: M个N维的向量，原始协方差矩阵就是一个C: N*N的矩阵。我们需要的到一个Y : R*M的矩阵，它的协方差矩阵为：D : R*R。而协方差为0，就是希望对角线上的个每个元素（同一特征的而反差）都足够大，而其它元素（每个元素之间的反差）都是0.

实际上就是实现协方差矩阵的一个对角化。

对D做一个推导：

D = 1/M * Y * Y.T, Y = R * M, 则D = R*R。

我们需要一个变换矩阵：P(R,M)

1. 需要一个X （N*M）矩阵。

2. 01均值化。

3. 求出协方差矩阵C。

4. 求出协方差C的特征值（就是y每个元素的方差，从大到小沿对角线排列就可以构成D），和特征向量。

5. 将特征向量，按照特征量的大小排序，按实际需要，降维的多少，需要的数据量是多少，得到一个降维的矩阵p。

完整代码：

import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt 

class DimensionValueError(ValueError):
    """定义异常类"""
    pass

class PCA(object):
    """定义PCA类"""

    # n_components 可是是自己选的降维后的维度，也可以是PCA算法自动算出来他认为最优的维度（若不填）
    def __init__(self , x,n_components = None):
        """"x的数据结构应为： (ids,features)"""
        self.x = x
        self.dimension = x.shape[1]
        self.n_components = n_components
        # 希望降维后的维度小于原有的维度
        if n_components and n_components >= self.dimension:
            return DimensionValueError("n_components error")

    # x -> C
    def cov(self):
        """求x的协方差矩阵"""
        x_T = np.transpose(self.x) # 矩阵转置
        x_cov = np.cov(x_T)
        return x_cov

    #C -> 特征值和特征向量
    def get_feature(self):
        """求协方差矩阵C的特征值和特征向量"""
        x_cov = self.cov()
        a , b = np.linalg.eig(x_cov)
        m = a.shape[0]
        c = np.hstack((a.reshape((m,1)) , b)) # 得到特征值
        c_df = pd.DataFrame(c)
        c_df_sort = c_df.sort_values(0,ascending=False)
        return c_df_sort

    def explained_varience_(self):
        c_df_sort = self.get_feature()
        return c_df_sort.values[:,0]

    def paint_varience_(self):
        explained_varience_ = self.explained_varience_()
        plt.figure()
        plt.plot(explained_varience_,'k')
        plt.xlabel('n_components',fontsize=16)
        plt.xlabel('explained_varience_',fontsize=16)
        plt.show()

    def reduce_dimension(self):
        """根据指定维度降维/根据方差贡献率降维"""
        c_df_sort = self.get_feature()
        varience = self.explained_varience_()

        if self.n_components:
            p = c_df_sort.values[0:self.n_components,1:]
            y = np.dot(p,np.transpose(self.X)) #矩阵叉乘
            return np.transpose(y)

        varience_sum = sum(varience) #利用反差贡献率来自动选择降维后维度
        varience_radio = varience / varience_sum

        varience_contribution = 0
        for R in range(self.dimension):
            varience_contribution += varience_radio[R] #前R个反差贡献之和
            if varience_contribution >= 0.99: #前R个方差贡献度之和大于0.99，则认为前R个特征可以代表数据特征
                break

        p = c_df_sort.values[0:R + 1,1:] #取前R个特征维度
        y = np.dot(p,np.transpose(self.x)) #矩阵叉乘
        return np.transpose(y)

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()

x = tf.reshape(x_train,shape=(-1,784))
x.shape

if __name__ == '__main__':
    pca = PCA(x)
    y = pca.reduce_dimension()
    print(y.shape)
    pca.paint_varience_()

8.1.2. 稀疏编码

我们人收到外界刺激真正只是一少部分的神经元，感受到的一直是少数的局部特征，具有稀疏性，首次启发。有人提出稀疏编码的模型。

线性编码：给定一组基向量A = [a1,a2……an],将输入样本x表示这些基向量的线性组合。

如输入一张图片28*28，共784个点，输入的维度就是784，基向量是p，编码就是对D维空间的x找到其在p维空间的一个表示。每个基向量之间是独立的。输入样本可以通过Z和a重构出来。所以编码的主要工作找到一个完备的基向量a，PCA也是其中一个方法。但是PCA得到的一个向量是稠密的，没有稀疏性。

为什么要强调稀疏性呢？就比如医生看病，也许生病有100种特征，医生诊断的时候只会根据几种来判断病因。但是这几种特征应该具有完备性。

完备性：

如果有p个基向量刚好能支撑p维的欧氏空间，则这p个向量是完备的。如果可支撑的维度d大于p的话，则这个基向量是过完备的。而稀疏编码得到目的是找到一组“超完备”的基向量来进行编码。

在此基础上，我们可以加入很多空的点，以此让他变得稀疏。

稀疏编码的目标函数：

我们怎么判断x输出的稀疏编码与x之间相差多少？最简单的方法之一就是l2范数。我们希望对应的稀疏编码Az能够尽量完全代表x。

$L(A,Z) = \sum_{n=1}^{N}(\left \| x^{(n)} - Az^{(n)} \right \|^{2}+\eta (z^{(n)}))$

稀疏性主要看 $\eta z^{(n)}$ 部分， $z^{(n)}$ 是个系数衡量函数，当越稀疏，他的值就越小。最直接简单的的就是l0范数，即非0元素的个数，但是其不连续不可导，所以我们可以使用l1范数，即所有数的绝对值之和。即越靠近0的向量，就越接近稀编码。 $\eta$ 是个超参数。

在整个公式中，我们不知道的是A和z。怎么求呢？训练过程是：

1. 固定基向量A，对每个输入的x，计算其对应的最优编码Z，即L(A，Z)为最小值的时候

2. 固定上一步的得到的编码向量Z1，Z2……Zn，计算器最优的基向量A。

稀疏编码的优点：

1. 降低计算量。

2. 可解释性，只有非常少数的非零元素，有生物的解释性。

3. 实现特征的自动选择，只选择和输入样本相关的最少特征，从而更好地表示输入呀昂本，降低噪声，并减轻过拟合。

8.1.3. 自编码器

PCA或是稀疏编码本质上都是一个线性变换。那能不能通过神经网络这样一个非线性的方式来实现呢？神经网络一般训练方式需要一个输入x，以及标签y。那我们可不可以利用输入本身作为一个监督信号，从而指导网络的训练呢？即用f(x) -> x。

为了实现这个目的，我们可以把网络分为两个部分：编码器，解码器。

编码器：是将x得到一个映射关系，也相当与一个将降维的过程。

解码器：是反过来得到与输入相同维度的向量。

当然二者之间可以有很多隐藏层。

8.2. 自编码器在MNIST上的图片重建实战

import tensorflow as tf
import numpy as np
from tensorflow import keras
import matplotlib.pyplot as plt
from PIL import Image
tf.__version__

image_size = 28*28
h_dim = 20
num_epochs = 50
batch_size = 100
learning_rate = 1e-3
new_im = Image.new('L',(280,280))

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
x_train , x_test = x_train.astype(np.float32)/255. , x_test.astype(np.float32)/255.
train_db = tf.data.Dataset.from_tensor_slices(x_train)
train_db = train_db.shuffle(batch_size*5).batch(128).batch(batch_size)

test_db = tf.data.Dataset.from_tensor_slices(x_test)
test_db = train_db.batch(batch_size)

class AE(keras.Model):
    '''自编码器模型'''
    def __init__(self):
        super().__init__()
        # 创建Encoder网络
        self.encoder = keras.Sequential([
            keras.layers.Dense(256,activation='relu'),
            keras.layers.Dense(128,activation='relu'),
            keras.layers.Dense(h_dim),
        ] , name='decoder')

        # 创建Decoder网络
        self.decoder = keras.Sequential([
            keras.layers.Dense(128,activation='relu'),
            keras.layers.Dense(256,activation='relu'),
            keras.layers.Dense(image_size),
        ])
    def call(self, inputs, training=None, mask=None):
        # 编码
        h = self.encoder(inputs)
        # 解码
        x_hat = self.decoder(h)
        return x_hat

model = AE()
model.build(input_shape=(None,image_size))
model.summary()

for epoch in range(num_epochs):
    for step, x in enumerate(train_db):
        # step划分成批次的批次数，x就是[100,28,28]
        x = tf.reshape(x, [-1,784])
        with tf.GradientTape() as tape:
            # 前向传播
            x_reconstruction_logits = model(x) # 类似于通过前向传播求出的 预估值
            # 计算loss
            reconstruction_loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=x,logits=x_reconstruction_logits)
            #对100张图片求出平均的loss
            reconstruction_loss = tf.reduce_mean(reconstruction_loss)
        # 自动求导
        gradients = tape.gradient(reconstruction_loss ,model.trainable_variables)
        # 自动更新
        tf.optimizers.Adam(learning_rate).apply_gradients(zip(gradients,model.trainable_variables))

        if epoch % 100 == 0:
            print("epoch: ",epoch," step: ",step," loss: ",reconstruction_loss)

    #每次迭代完成后，构建图片进行比较
    out_logits = model(x[:batch_size//2])
    out = tf.nn.sigmoid(out_logits)
    out = tf.reshape(out, [-1,28,28]).numpy() * 255.

    x = tf.reshape(x[:batch_size // 2], [-1,28,28])
    x_concat = tf.concat( [x,out] ,axis = 0).numpy() * 255.
    x_concat = x_concat.astype(np.uint8)

    index = 0
    for i in range(0,280,28):
        for j in range(0,280,28):
            im = x_concat[index]
            im = Image.fromarray(im,mode='L')
            new_im.paste(im,(i,j))
            index += 1

    new_im.save('images/_%d.png' % (epoch))
    plt.imshow(np.asarray(new_im))
    plt.show()
    print('new image saved !')

# 取测试机中的一个批次的图片
x = next(iter(test_db))

8.3. 自编码器变种

8.3.1 稀疏自编码器

给自编码器的隐藏层z上增加了稀疏性限制,希望编码层的输出维度大于输入的维度。

公式中的稀疏性限制ρ可以是KL散度。是神经元激活的概率。

8.3.2. 堆叠自编码器

通过逐层堆叠的方式训练一个深层的自编码器。

由于深层的网络会发生过拟合，以及参数量过大。我们就可以使用Droupout编码器，混合使用，来降低过拟合。

8.3.3. 降噪自编码器

给输入数据随即增加一些噪声，随机的将x的一些维度值设置为0，得到一个被破坏的向量x。

8.3.4. 对抗自编码器

通过任意先验分布与VAE隐藏代码向量的聚合后验匹配。将聚合后的后验与先验相匹配，确保从先验空间的任何部分产生的样本是有意义的。

原来的自编码器是实值与实值的比较，而变分自编码器，是将实值用概率值的方式考虑。实际上变分自编码器VAE是普通自编码器与贝叶斯模型的混合。

8.3.4. 变分自编码器

原来的自编码器，本质上是给定一个x，我们找到一个映射关系到Z。这本质上是一个判别模型，最后z解码后生成的x’本质上还是x生成的。那我们能不能通过隐藏的z来生产一个x‘呢？

可以从x得到隐变量z相应的一些概率分布。通过全概率分布p(x) = p(x|z)p(z),则可以得到一个p(x)的概率分布。

假设服从正态分布的Z，在生成器decoder的作用下，可以生成新的样本。那新的样本和原来的分布是否相等呢？

我们不能用KL散度来计算分布是否相等。

z（隐变量）可以理解为是有可能影响分布的一些可能性。生成的x肯定也会有一些z的特性

上述公式，假设p(z)是满足正态分布的，而p(x|z)：即贝叶斯公式。

而公式中的p（z|x）可以用变分推断的方式，用一个q（z|x）来逼近，因为可以证明，总有方法使得一个映射到另一个概率分布。我们可以用KL散度来比较两种分布的差距。