Matlab数字图像处理学习记录【5】——彩色图像处理

一.Matlab中彩色图像的表示方法

一般来说在IPT里，彩色图像被当做索引图像和RGB图像来处理。所以重点学习这两个图像。

1.1RGB图像

这个没啥说的，就是将红绿蓝三色图像组合起来。当然，可以用cat将图像组合起来。
frgb = cat(dim, fr, fg, fb) dim是将后者矩阵叠加的维度。此处写3即可。
当然，也可以通过切片的方式来分割成图像分量：
fR = frgb(:, :, 1); 、fG = frgb(:, :, 2);、fB = frgb(:, :, 3);
创建函数，建立一个可以自定义观测角度的RGB立方体：

%使用rgbcube展示RGB彩色立方体示意图
function rgbcube(vx,vy,vz)
%rgbcube用于展示RGB彩色立方体示意图，其中观测的角度是(vx,vy,vz)。如果无输入角度，默认为（10，10，4）.
patch('Vertices',vertices_matrix,'Faces',faces_matrix,'FaceVertexCData',colors,'FaceColor','interp','EdgeAlpha',0)
%处理观测点
if nargin==0
    vx=10;vy=10;vz=4;
elseif nargin~=3
    error('Wrong number of inputs.')
end
axis off%取消对坐标轴的一切设置
view([vx, vy, vz])%输入观测点
axis square%使绘图区域为正方形

传参即可

rgbcube(0.7, 0.2, 0.3)

1.2索引图像

索引图像有两个分量。一个是数据矩阵X，一个是色彩映射矩阵map。
映射矩阵map存放颜色数据，长度由颜色的数量决定。数据矩阵则是存放指向映射矩阵的索引值。
这样做的好处就是，假设需要更换颜色类型。那么直接修改map即可，而不需要对数据矩阵进行复杂的变换操作。
若需要显示该图像，一般使用
imshow(X, map)或者image(X)、colormap(map).
可以通过[Y, newmap] = imapprox(X, map, n)
利用该函数，将X和map 变为不超过n中颜色的新组合Y和newmap但注意其对值矩阵的缩放。
指定色彩图像，可以用：
map(k, :) = [r(k), g(k), b(k)]
其中[r(k), g(k), b(k)]是RGB值，指定色彩映射的一行，变化k的值，就可以填充满整个图。
修改图像的背景色可以用
whitebg()，推荐填RGB值，当然也可以填名字：

在显示图像，或者置映射map的时候，我们可以用预设的彩色映射：

1.3用来处理RGB图像或索引图像的IPT函数

比如dither，可以用于灰度图和彩色图像(但是我试了RGB不行, 只能单通道)，比如在灰度图里，使用它可以在白色背景上添加黑点得到灰色调。也就是用二值化的图模拟灰度图。
用法bw = dither(gray_image)

gray_image = imread('gray.jpg');
bw = dither(gray_image);
subplot(1,2,1);
imshow(gray_image);
subplot(1,2,2);
imshow(bw);

在处理彩色图像的时候，抖动函数需要和rgb2ind结合使用，这个函数后面讨论。
然后就是通过一个阈值，将gray图生成一幅索引图像的：X = grayslice(gray_image, n)
其中阈值为：$\frac{1}{n}、\frac{2}{n}、\frac{3}{n}\dots \frac{n-1}{n}$
如果将标量n改为向量v，则可以自定义映射map的大小。其中向量v的取值在[0,1]之间，函数会自己缩放。
利用[X, map] = gray2ind(gray_image, n)缩放后，会用彩色映射，也就是表6.2中的gray(n)进行转换。若n省略，则默认64.
ind2gary()同理。
[X, map] = rgb2ind(rgb_image, n, dither_option) 参数同灰度图，不过多了个参数。
若填字符串dither则执行抖动，会提高空间分辨率达到更好的颜色分辨力。nodither则是将颜色映射到新图上最金额近的颜色。
rgb_image = ind2rgb(X, map)和gray_image = rgb2gray(rgb_image)同理。

二.转换值其他彩色空间

2.1NTSC彩色空间

NTSC色彩空间中，颜色由亮度Y、色调I、饱和度Q组成。
亮度描述灰度信息，色调和饱和度描述彩色信息。
转换公式：
$$\left[\begin{array}{c}Y\\ I\\ Q\end{array}\right]=\left[\begin{array}{ccc}0.299& 0.587& 0.114\\ 0.596& -.0274& -0.322\\ 0.211& -0.523& 0.12\end{array}\right]\left[\begin{array}{c}R\\ G\\ B\end{array}\right]$$
转换函数为：yiq_image = rgb2ntsc(rgb_image)
输出为double类图像，当然还是可以通过切片提取Y、I、Q。
类似：
$$\left[\begin{array}{c}R\\ G\\ B\end{array}\right]=\left[\begin{array}{ccc}1.000& 0.956& 0.621\\ 1.000& -.0272& -0.647\\ 0.211& -1.106& 1.703\end{array}\right]\left[\begin{array}{c}Y\\ I\\ Q\end{array}\right]$$
函数rgb_image = ntsc2rgb(yiq_image)

2.2YCbCr彩色空间

$$\left[\begin{array}{c}Y\\ Cb\\ Cr\end{array}\right]=\left[\begin{array}{c}16\\ 128\\ 128\end{array}\right]+\left[\begin{array}{ccc}64.481& 128.553& 24.966\\ -37.797& -74.203& 112.000\\ 112.000& -93.786& -18.214\end{array}\right]\left[\begin{array}{c}R\\ G\\ B\end{array}\right]$$
函数ycbcr_image = rgb2ycbcr(rgb_image)和rgb_image = ycbCr2rgb(ycbcr_image)

2.3HSV色彩空间

HSV(色调、饱和度、亮度)是较常用的一种模型。

色调是围绕彩色六边形的角度来描述的。沿锥体的轴来测量值，也就是我这里说的亮度。V = 0时，轴的末端为黑色，V=1是，州的末端为白色。比如要制作呼吸灯，那么保持HS不变，变化V的大小，即可完成在近似相同的颜色的情况下调整亮度。RGB转HSV的方法就是将RGB坐标系映射指柱坐标系，这里没有推导，可以去别处看。
函数是：hsv_image = rgb2hsv(rgb_image)和rgb_image = hsv2rgb(hsv_image)。

2.4CMY和CMYK彩色空间

一般用于打印机内部的颜色。

理论上，等量的颜料原色即青色、品红色和黄色混合会产生黑色。在实践中,将这些颜色加以混合来印刷会生成一幅模糊不清的黑色图像。所以，为了生成一种纯正的黑色(打印中使用的主要颜色)，便要添加第四种颜色，即黑色，从而出现了CMYK彩色模型。这样，当出版者谈论“四色印刷”时，他们其实是在说CMY彩色模型的三种颜色加上黑色。
函数：cmy_image = imcomplement(rgb_image)和rgb_image = imcomplement(cmy_image)

2.5 HSI彩色空间

HSI(hue色度；saturation饱和度，intensity亮度)彩色空间，该模型将亮度分量用途一幅彩色图像中携带的彩色信息分开，是一种对于开发基于彩色描述的图像处理算法是个理想的工具。
其推导过程：

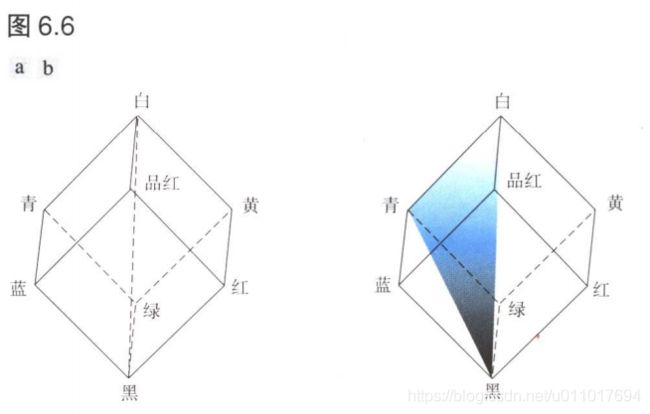
• 如在6.1.1节中讨论过的那样，RGB彩色图像是由三幅单色的亮度图像构成的，所以一定可以从一幅RGB图像中提取出亮度。若拿图6.2所示的彩色立方体来看，一切就很清楚。假设我们站在黑色顶点(0,0,0)处，如图6.6(a)所示，它的正上方是白色顶点（1,1,1)。再同图6.2联系起来看，亮度是沿着连接着两个点的连线分布的。在图6.6所示的排列中,这条连接黑色和白色顶点的线(亮度轴）是垂直的。因此，若想确定图6.6中任意彩色点的亮度分量，我们就需要经过一个包含该点且垂直于亮度轴的平面。这个平面和亮度轴的交点就给出了范围在[0,1]之间的亮度值。我们也注意到饱和度是一个与亮度轴之间的距离的函数。事实上，亮度轴上的点的饱和度为零,亮度轴上的所有点都是灰色的这个事实是很显然的。为了弄清从一个给定RGB点确定色调的方式，可参考图6.6(b)，它显示了一个由三个点（黑色、白色和青色)所定义的平面。该平面上含有黑色和白色顶点的事实告诉我们亮度轴同样在这个平面上。此外,可以看到由亮度轴和立方体边界共同定义的平面上的所有点都有相同的色调(在此例中为青色)。这是因为在一个彩色三角形内，颜色是由这三个顶点颜色的多种多样的组合或者混合而成的。若这些顶点中的两个是黑色和白色,第三个顶点是-一个彩色的点,则这个三角形中所有点的色调都是相同的，因为白色和黑色分量对于色彩的变化没有影响(当然，在这个三角形中，点的亮度和饱和度会变化)。以垂直的强度轴旋转这个个阴影平面，可以获得不同的色调。
  
• 图6.7(b)显示了六边形和一个任意的彩色点(用点的形式显示)。这个点的色调是由其与某参考点的夹角决定的。一般来说(但也不总是如此)，与红色轴的夹角为0°，色调在此处按逆时针方向增加。饱和度(距垂直轴的距离）是从原点到该点的向量的长度。注意，原点由该彩色平面与垂直亮度轴的交点定义。HSI彩色空间的重要分量包括垂直亮度轴、到彩色点的向量长度以及该向量与红色轴间的夹角。因此,当用刚才讨论过的六边形甚至如图6.7©和如图6.7(d)所示的三角形或圆形时,这些形式定义一个HSI平面是不足为奇的。选择哪种形状是不重要的,因为任意一种形状都可以通过几何变换变换成另一种形状。图6.8显示了基于彩色三角形和圆形的HSI模型。
  
  
  那么从RGB变HSI的过程：
  H分量：
  $$\begin{gathered} H=\{\begin{array}{ll}\theta ,& 若B\le G\\ 360-\theta ,& 若＞G\end{array} \\ 其中\theta =arccos\{\frac{0.5[R-G]+R-B}{[(R-G{)}^2+(R-B)(G-B{)}^{0.5}]}\} \end{gathered}$$
  S分量：
  $$S=1-\frac{3}{(R+B+G)}[min(R,G,B)]$$
  I分量：
  $$I=\frac{1}{3}(R+B+G)$$
  若RGB输入为[0,1]将H/360°，则HSI输出也为[0,1]
  若将HSI转换为RGB则是根据H来决定：

1. RG区(0°≤H＜120°)
   $$\begin{gathered} R=I[1+\frac{ScosH}{cos(60°-H)}] \\ B=I(1-S) \\ G=3I-(R+B) \end{gathered}$$
2. GB区(120°≤H＜240°)
   $$\begin{gathered} H=H-120° \\ G=I[1+\frac{ScosH}{cos(60°-H)}] \\ R=I(1-S) \\ B=3I-(R+G) \end{gathered}$$
3. BR区(240°≤H＜360°)
   $$\begin{gathered} H=H-240° \\ B=I[1+\frac{ScosH}{cos(60°-H)}] \\ G=I(1-S) \\ R=3I-(G+B) \end{gathered}$$
   那么代码为：

function rgb = hsi2rgb(hsi) 
%HSI2RGB Converts an HSI image to RGB. 
%   RGB = HSI2RGB(HSI) converts an HSI image to RGB, where HSI is 
%   assumed to be of class double with:   
%     hsi(:, :, 1) = hue image, assumed to be in the range 
%                    [0, 1] by having been divided by 2*pi. 
%     hsi(:, :, 2) = saturation image, in the range [0, 1]. 
%     hsi(:, :, 3) = intensity image, in the range [0, 1]. 
% 
%   The components of the output image are: 
%     rgb(:, :, 1) = red. 
%     rgb(:, :, 2) = green. 
%     rgb(:, :, 3) = blue. 
%   Copyright 2002-2004 R. C. Gonzalez, R. E. Woods, & S. L. Eddins 
%   Digital Image Processing Using MATLAB, Prentice-Hall, 2004 
%   $Revision: 1.5 $  $Date: 2003/10/13 01:01:06 $ 
% Extract the individual HSI component images. 
H = hsi(:, :, 1) * 2 * pi; 
S = hsi(:, :, 2); 
I = hsi(:, :, 3); 
% Implement the conversion equations. 
R = zeros(size(hsi, 1), size(hsi, 2)); 
G = zeros(size(hsi, 1), size(hsi, 2)); 
B = zeros(size(hsi, 1), size(hsi, 2)); 
% RG sector (0 <= H < 2*pi/3). 
idx = find( (0 <= H) & (H < 2*pi/3)); 
B(idx) = I(idx) .* (1 - S(idx)); 
R(idx) = I(idx) .* (1 + S(idx) .* cos(H(idx)) ./ cos(pi/3 - H(idx))); 
G(idx) = 3*I(idx) - (R(idx) + B(idx)); 
% BG sector (2*pi/3 <= H < 4*pi/3). 
idx = find( (2*pi/3 <= H) & (H < 4*pi/3) ); 
R(idx) = I(idx) .* (1 - S(idx)); 
G(idx) = I(idx) .* (1 + S(idx) .* cos(H(idx) - 2*pi/3) ./ cos(pi - H(idx))); 
B(idx) = 3*I(idx) - (R(idx) + G(idx)); 
% BR sector. 
idx = find( (4*pi/3 <= H) & (H <= 2*pi)); 
G(idx) = I(idx) .* (1 - S(idx)); 
B(idx) = I(idx) .* (1 + S(idx) .* cos(H(idx) - 4*pi/3) ./cos(5*pi/3 - H(idx))); 
R(idx) = 3*I(idx) - (G(idx) + B(idx)); 
% Combine all three results into an RGB image.  Clip to [0, 1] to 
% compensate for floating-point arithmetic rounding effects. 
rgb = cat(3, R, G, B); 
rgb = max(min(rgb, 1), 0); 

function hsi = rgb2hsi(rgb) 
%RGB2HSI Converts an RGB image to HSI. 
%   HSI = RGB2HSI(RGB) converts an RGB image to HSI. The input image 
%   is assumed to be of size M-by-N-by-3, where the third dimension 
%   accounts for three image planes: red, green, and blue, in that 
%   order. If all RGB component images are equal, the HSI conversion 
%   is undefined. The input image can be of class double (with values 
%   in the range [0, 1]), uint8, or uint16.  
% 
%   The output image, HSI, is of class double, where: 
%     hsi(:, :, 1) = hue image normalized to the range [0, 1] by 
%                    dividing all angle values by 2*pi.  
%     hsi(:, :, 2) = saturation image, in the range [0, 1]. 
%     hsi(:, :, 3) = intensity image, in the range [0, 1]. 

%   Copyright 2002-2004 R. C. Gonzalez, R. E. Woods, & S. L. Eddins 
%   Digital Image Processing Using MATLAB, Prentice-Hall, 2004 
%   $Revision: 1.4 $  $Date: 2003/09/29 15:21:54 $ 

% Extract the individual component immages. 
rgb = im2double(rgb); 
r = rgb(:, :, 1); 
g = rgb(:, :, 2); 
b = rgb(:, :, 3); 

% Implement the conversion equations. 
num = 0.5*((r - g) + (r - b)); 
den = sqrt((r - g).^2 + (r - b).*(g - b)); 
theta = acos(num./(den + eps)); 

H = theta; 
H(b > g) = 2*pi - H(b > g); 
H = H/(2*pi); 

num = min(min(r, g), b); 
den = r + g + b; 
den(den == 0) = eps; 
S = 1 - 3.* num./den; 

H(S == 0) = 0; 

I = (r + g + b)/3; 

% Combine all three results into an hsi image. 
hsi = cat(3, H, S, I); 

三.彩色图像处理基础

一般把彩色图像处理细分为三个主要类别：

1. 颜色变换
2. 单独颜色平面的空间处理
3. 颜色向量处理

第一类就类似于处理每个彩色平面的像素，以像素值为基础，处理方法类似。而第二类则对各个彩色平面空间进行空间滤波。第三类则是同时处理所有分量。每个像素则为一个向量：
$$c=\left[\begin{array}{c}{c}_R\\ c_G\\ c_B\end{array}\right]=\left[\begin{array}{c}R\\ G\\ B\end{array}\right]$$
若用x，y表示则是：
$$c(x,y)=\left[\begin{array}{c}{c}_R(x,y)\\ c_G(x,y)\\ c_B(x,y)\end{array}\right]=\left[\begin{array}{c}R(x,y)\\ G(x,y)\\ B(x,y)\end{array}\right]$$
为了使独立的彩色分量和以向量为基础的处理都相同，必须满足两个条件：
首先，处理要对向量和标量都可以用。
对向量的每个分量的运算必须独立于其他分量。

四.彩色变换

在单个彩色模型的情况下，处理彩色图像的彩色分量或单色图像的亮度分量。对于彩色图像有：$s_i=T_i(r_i),i=1,2,...,n$若该图像是单色的，则方程可以改为：$s_i=T_i(r),i=1,2,...,n$
其中，r表示灰度级的值，s_i和T 如上所示，n是s_i中的彩色分量数。该方程描述把灰度级转换成任意颜色的映射，这一处理常称为伪彩色变换或伪彩色映射。注意，若令r₁=r₂= r₃=r，则第一个方程可用来处理RGB中的单色图像。
第3章已介绍过一些灰度变换:

1. imcomplement，它计算一幅图像的负片，与被变换图像的灰度级内容无关。
2. 另外，如果与灰度级分布有关的histeq是自适应的，则一旦估计了必要的参数，变换就会固定。
3. imadjust，它要求使用者选择合适的曲线形状参数，且最好是交互式地指定。当用伪彩色和全彩色映射时,尤其是涉及到人的观察和说明(如彩色平衡)时,存在相似的情况。

在这些应用中,直接产生候选函数的图形表示并在被处理图像上观察其组合效果（实时）的方法，是选择合适的映射函数的最好方法。
使用双插值z=interp1q(x, y, xi)可以用图形来指定映射函数。
它返回一个列向量，该向量包括在点xi处使用-维函数z线性插值的值。列向量x和y指定控制点的水平和垂直坐标。x的元素必须单调增长。z的长度等于xi的长度。
例如:z = interp1q([0 255]', [0 255]', [0: 255]')则产生了一个产生一个有着256个元素的一一映射，以连接控制点（0,0）和(255,255)，即z=[ 012…255]’。
三次样条插值函数则是：z=interp1q(x, y, xi)
交互式产生变换函数可以用ice生成：
g = ice ( 'Property Name ', 'Property value', . . .)
其中，Property Name和Property value必须成对出现，并且这些点表示由相应输入对所组成的模式的重复。表6.4列出了ice函数中的正确搭配。一些例子将在本章稍后给出。
关于wait参数，当显式地或默认地选择on时,输出g是处理后的图像。在这种情况下，ice将控制处理，包括光标，因而在命令窗口不必键入任何命令，直到函数关闭，这时最后的结果就是图像g。当选择off时，g为处理后的图像的句柄，并且控制会立即返回到命令窗口;因此，在函数ice仍处于活动状态时，可以键入新的命令。为了用句柄g获得图像的属性，我们使用get函数h=get(g)



不过ice这个函数好像没有，但是Google到了其源码，下载地址：http://fourier.eng.hmc.edu/e161/dipum/ice.m
然后发现这个网页基本上涵盖了该书所有要自定义的函数。
下载ice.m和ice.fig即可运行：

f = imread('./test.jpg');
ice('image', f)

五.彩色图像的空间滤波

5.1彩色图像平滑

其思想还是对三个通道的颜色“求平均”，假设S_xy是彩色图像中以(x,y)为中心的领域的一组坐标。其平均值是：
$$\bar{c}(x,y)=\frac{1}{K}\sum _{(s,t)\in S_{xy}}c(s,t)$$
将前面的平滑滤波imfilter通过对三个通道分别滤波，再叠加即可成为fc_imfilter。
当然也可以对HSI图像进行滤波。

fc = imread('./test.jpg');
R = fc(:,:,1);
G = fc(:,:,2);
B = fc(:,:,3);
h = rgb2hsi(fc);
H = h(:, :, 1); S = h(:, :, 2) ; I = h(:, :, 3);
w = fspecial('average', 25);
I_filtered = imfilter(I, w,'replicate');
h = cat(3,H, S, I_filtered);
f = hsi2rgb(h);
f = min(f, 1);
fR = imfilter(R, w, 'replicate');
fG = imfilter(G, w, 'replicate');
fB = imfilter(B, w, 'replicate');
frgb = cat(3,fR, fG, fB);
subplot(1,3,1);
imshow(fc);
subplot(1,3,2);
imshow(frgb);
subplot(1,3,3);
imshow(f);

5.2彩色图像锐化

同理，分通道锐化，叠加：
$${\nabla }^2[c(x,y)]=\left[\begin{array}{c}{\nabla }^{2}R(x,y)\\ {\nabla }^{2}G(x,y)\\ {\nabla }^{2}B(x,y)\end{array}\right]$$

fb = imread('./test.jpg');
lapmask = [1 1 1; -8 1 1; 1 1 1];
fen = imsubtract(fb, imfilter(fb, lapmask, 'replicate'));
subplot(1, 2, 1);
imshow(fb);
subplot(1, 2, 2);
imshow(fen)

六.在RGB向量空间直接处理

因为有些时候，叠加后的信息，并不等于分离后再叠加。所以需要直接对[RGB]这向量进行操作。

6.1使用梯度的彩色边缘检测

二维函数f(x,y)的梯度定义为向量：
$$\nabla f=\left[\frac{G_x}{G_y}\right]=\left[\frac{\frac{\partial f}{\partial x}}{\frac{\partial f}{\partial y}}\right]$$
该向量幅值为：
$$\nabla f=mag(\nabla f)=[G_x^2+G_y^2{]}^{1/2}=[(\partial f/\partial x{)}^2+(\partial f/\partial y{)}^2{]}^{1/2}$$
通常，该量用绝对值代替：
$$\partial f\approx |G_x|+|G_y|$$
梯度：
$$\alpha (x,y)=arctan(\frac{G_y}{G_x})$$
当然离散化的情况下，可以用卷积核代替：

将这个思维拓展到RGB上：
$$\begin{gathered} u=\frac{\partial R}{\partial x}r+\frac{\partial G}{\partial x}g+\frac{\partial B}{\partial x}b \\ 和 \\ v=\frac{\partial R}{\partial y}r+\frac{\partial G}{\partial y}g+\frac{\partial B}{\partial y}b \end{gathered}$$
点积：
$$\begin{gathered} g_{xx}=u\cdot u \\ {g}_{yy}=y\cdot y \\ {g}_{xy}=x\cdot y \end{gathered}$$
则可以得到：
c(x,y)的最大变化率的方向由角度
$$\theta (x,y)=\frac{1}{2}arctan[\frac{2g_{xy}}{(g_{xx}-g_{yy})}]$$
梯度值：
$$F_{\theta }=\{\frac{1}{2}[(g_{xx}+g_{yy})+(g_{xx}-g_{yy})cos2\theta +2g_{xy}sin2\theta ]{\}}^{1/2}$$
封装成函数：colorgrad:

function [VG, A, PPG]= colorgrad(f, T)
%COLORGRAD Computes the vector gradient of an RGB image.
%   [VG, VA, PPG] = COLORGRAD(F, T) computes the vector gradient, VG,
%   and corresponding angle array, VA, (in radians) of RGB image
%   F. It also computes PPG, the per-plane composite gradient
%   obtained by summing the 2-D gradients of the individual color 
%   planes. Input T is a threshold in the range [0, 1]. If it is
%   included in the argument list, the values of VG and PPG are
%   thresholded by letting VG(x,y) = 0 for values <= T and VG(x,y) =
%   VG(x,y) otherwise. Similar comments apply to PPG.  If T is not
%   included in the argument list then T is set to 0. Both output
%   gradients are scaled to the range [0, 1].

%   Copyright 2002-2004 R. C. Gonzalez, R. E. Woods, & S. L. Eddins
%   Digital Image Processing Using MATLAB, Prentice-Hall, 2004
%   $Revision: 1.6 $  $Date: 2003/11/21 14:27:21 $

if (ndims(f) ~= 3) | (size(f, 3) ~= 3)
   error('Input image must be RGB.');
end

% Compute the x and y derivatives of the three component images 
% using Sobel operators.
sh = fspecial('sobel');
sv = sh';
Rx = imfilter(double(f(:, :, 1)), sh, 'replicate');
Ry = imfilter(double(f(:, :, 1)), sv, 'replicate');
Gx = imfilter(double(f(:, :, 2)), sh, 'replicate');
Gy = imfilter(double(f(:, :, 2)), sv, 'replicate');
Bx = imfilter(double(f(:, :, 3)), sh, 'replicate');
By = imfilter(double(f(:, :, 3)), sv, 'replicate');

% Compute the parameters of the vector gradient. 
gxx = Rx.^2 + Gx.^2 + Bx.^2;
gyy = Ry.^2 + Gy.^2 + By.^2;
gxy = Rx.*Ry + Gx.*Gy + Bx.*By;
A = 0.5*(atan(2*gxy./(gxx - gyy + eps)));
G1 = 0.5*((gxx + gyy) + (gxx - gyy).*cos(2*A) + 2*gxy.*sin(2*A));

% Now repeat for angle + pi/2. Then select the maximum at each point.
A = A + pi/2;
G2 = 0.5*((gxx + gyy) + (gxx - gyy).*cos(2*A) + 2*gxy.*sin(2*A));
G1 = G1.^0.5;
G2 = G2.^0.5;
% Form VG by picking the maximum at each (x,y) and then scale
% to the range [0, 1].
VG = mat2gray(max(G1, G2));

% Compute the per-plane gradients.
RG = sqrt(Rx.^2 + Ry.^2);
GG = sqrt(Gx.^2 + Gy.^2);
BG = sqrt(Bx.^2 + By.^2);
% Form the composite by adding the individual results and
% scale to [0, 1].
PPG = mat2gray(RG + GG + BG);

% Threshold the result.
if nargin == 2
   VG = (VG > T).*VG;
   PPG = (PPG > T).*PPG;
end

写代码：

f = imread('./test.jpg');
[VG, A, PPG] = colorgrad(f);
subplot(2,2,1);
imshow(f);
subplot(2,2,2);
imshow(VG);
subplot(2,2,3);
imshow(A);
subplot(2,2,4);
imshow(PPG);

6.2 RGB向量空间中的图像分割

使用RGB彩色向量进行彩色区域分割是很简单的。假设我们的目的是在RGB图像中分割一个特定彩色范围的物体。给定一组感兴趣的彩色(或彩色范围)描述的彩色样本点,我们获得一个“平均”的颜色估计，它是我们希望分割的那种颜色。让这种平均色用RGB列向量m来定义。分割的目的是对图像中的每一个RGB像素进行分类,使其在指定的范围内有一种颜色或没有颜色。为执行这一比较，我们需要一个相似性度量。最简单的度量之一是欧几里得距离。令z表示RGB空间的任意点。若z和m之间的距离小于指定的阈值T,则我们说z相似于m。z和m之间的欧几里得距离公式得：
$$\begin{gathered} D(z,m)=||z-m|| \\ =[(z-m{)}^T(z-m){]}^{1/2} \\ =[(z_R-m_R{)}^2+(z_G-m_G{)}^2+(z_B-m_B{)}^2{]}^{1/2} \end{gathered}$$
其中||·||是参量的范数，下标R、G和B表示向量m和z的RGB分量。D(z,m)≤T的点的轨迹是一个半径为T的实心球体。由定义可知，包含在球体内部或表面的点满足特定的彩色准则;而球体外面的点则不满足。在图像中对这两组点编码,如黑的和白的，产生一幅二值分割图像。
对前述方程一个有用归纳是距离：
$$D(z,m)=[(z-m{)}^T{C}^{-1}(z-m){]}^{1/2}$$
其中,C是我们要分割的彩色的样值表示的协方差矩阵。该距离称为Mahalanobis距离。D(z, m)≤T的点的轨迹描述了一个实心三维椭圆体，它的重要属性是其主轴取在最大的数据扩展方向上。当C等于单位矩阵I时,Mahalanobis距离约简为欧几里得距离。除了现在数据包含在椭球体内而不是包含在圆球体内之外，分割和在前段描述过的一样。

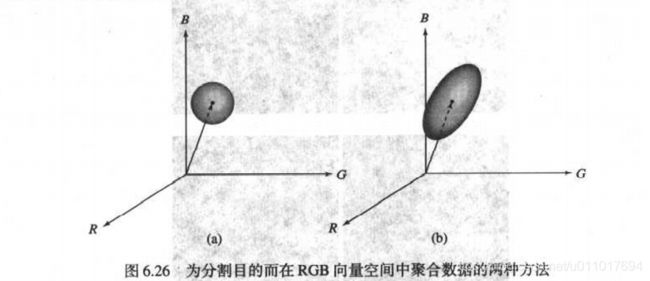
其函数为：S = colorseg(method, f, T, parameters)
其中，method不是euclidean就是mahalanobis，f是待分割的RGB 图像，T是前边描述过的阈值。若选择euclidean，则输入参数是m，若选择mahalanobis,则输人参数是m和c。参数m是一个在上面描述过的向量m，它的形式不是行就是列，并且c是3×3协方差矩阵C。
输出s是一幅二值图像（和原始图像同样大小),在未通过阈值测试的点包含0，在通过了阈值测试的点包含1。1表示从基于彩色内容的f中分割的区域。
colorseg的代码：在http://fourier.eng.hmc.edu/e161/dipum/下载：imstack2vectors.m、covmatrix.m、colorseg.m

f = imread('test.jpg');
mask = roipoly(f);
red = immultiply(mask, f(:,:,1));
green = immultiply(mask, f(:,:,2));
blue = immultiply(mask, f(:,:,3));
g = cat(3, red, green, blue);
figure;
[M, N, K] = size(g);
I = reshape(g, M * N, 3);
idx = find(mask);
I = double(I(idx, 1:3));
[C, m] = covmatrix(I);
d = diag(C);
sd = sqrt(d)'
subplot(1,4,1);
E25 = colorseg('euclidean', f, 25, m);
imshow(E25);
subplot(1,4,2);
E50 = colorseg('euclidean', f, 50, m);
imshow(E50);
subplot(1,4,3);
E75 = colorseg('euclidean', f, 75, m);
imshow(E75);
subplot(1,4,4);
E100 = colorseg('euclidean', f, 100, m);
imshow(E100);

先选中卡通人物的衣服：

然后得到图像：

其中C的主对角线包括RGB分量的方差，所以我们必须提取这些元素并计算它们的平方根，也就是代码中的d = diag(C); sd = sqrt(d)'
当我们的值越大，我们图像分割的效果越不明显。
当值在10的时候，对于此图，效果是最好的：