YOLOX网络结构详解

论文名称：YOLOX: Exceeding YOLO Series in 2021
论文下载地址：https://arxiv.org/abs/2107.08430
论文对应源码地址：https://github.com/Megvii-BaseDetection/YOLOX

---

---

0 前言

在之前文章中我们已经聊过YOLO v5了，今天我们再来聊聊YOLOX。YOLOX是旷视科技在2021年发表的一篇文章，当时主要对标的网络就是很火的YOLO v5，如果对YOLO v5不了解的可以看下我之前的文章。那么在YOLOX中引入了当年的哪些黑科技呢，简单总结主要有三点，decoupled head、anchor-free以及advanced label assigning strategy(SimOTA)。YOLOX的性能如何呢，可以参考原论文图一，如下图所示，YOLOX比当年的YOLO v5略好一点，并且论文中说他们利用YOLOX获得了当年的Streaming Perception Challenge的第一名。那这里可能有人会问了，在自己的项目中YOLO v5和YOLOX到底应该选择哪个。我个人的建议是，如果你的数据集图像分辨率不是很高，比如640x640，那么两者都可以试试。如果你的图像分辨率很高，比如1280x1280，那么我建议使用YOLO v5。因为YOLO v5官方仓库有提供更大尺度的预训练权重，而YOLOX当前只有640x640的预训练权重（YOLOX官方仓库说后续会提供更大尺度的预训练权重，可过了快一年了还没有音讯）。

---

1 网络结构

下图是我根据源码绘制的YOLOX-L网络结构。因为它是基于YOLO v5构建的，所以Backbone以及PAN部分和YOLO v5是一模一样的，注意这里说的YOLO v5是对应tag:v5.0版本的，而我们之前讲的YOLO v5文章中是tag:v6.1版本，所以在Backbone部分有些细微区别，大家自行对比一下就知道了，这里不去赘述。如果看不懂的可以翻下之前写的YOLO v5文章。

那YOLOX和YOLO v5在网络结构上有什么差别呢，主要的差别就在检测头head部分。之前的检测头就是通过一个卷积核大小为1x1的卷积层实现的，即这个卷积层要同时预测类别分数、边界框回归参数以及object ness，这种方式在文章中称之为coupled detection head（耦合的检测头）。作者说采用coupled detection head是对网络有害的，如果将coupled detection head换成decoupled detection head（解耦的检测头）能够大幅提升网络的收敛速度。在论文的图3中展示了YOLO v3分别使用coupled detection head和decoupled detection head的训练收敛情况，明显采用decoupled detection head后收敛速度会更快（在论文的表2中显示采用decoupled detection head能够提升AP约1.1个点）。说句题外话相比与YOLO v3我更关心对于YOLO v5能提升多少AP，但文章中并没有相关数据。

那decoupled detection head到底长啥样，根据原论文的图2以及源码绘制的decoupled detection head结构如下。在decoupled detection head中对于预测Cls.、Reg.以及IoU参数分别使用三个不同的分支，这样就将三者进行了解耦。这里需要注意一点，在YOLOX中对于不同的预测特征图采用不同的head，即参数不共享。

---

2 Anchor-Free

近几年有关Anchor-Free的网络也层出不穷，之前我们也聊过一个Anchor-Free的网络FCOS，如果不了解的建议看下之前的文章。今天讲的YOLOX也是一个Anchor-Free的网络，并且借鉴了FCOS中的思想。刚刚在上面我们已经简单聊到了YOLOX的decoupled detection head，它对预测特征图（feature map/Grid 网格）上的每一个位置都预测了$nu{m}_{cls}+4+1$个参数，其中$nu{m}_{cls}$代表检测的目标类别数，4代表网络预测的目标边界框参数，1代表object ness（图中标的是IoU.）。
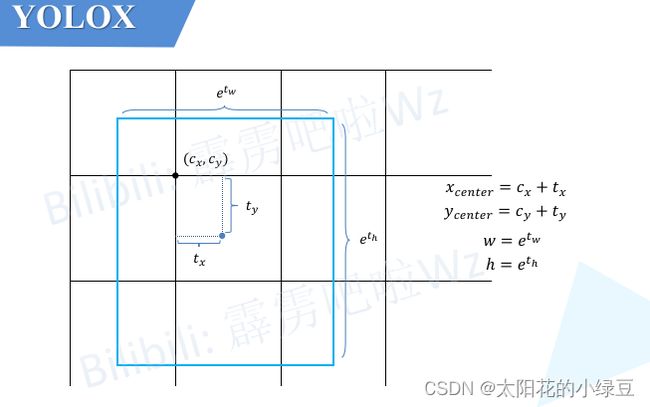
由于YOLOX是Anchor-Free的网络，所以head在每个位置处直接预测4个目标边界框参数$[t_x,t_y,t_w,t_h]$如下如所示，这4个参数分别对应预测目标中心点相对Grid Cell左上角$(c_x,c_y)$的偏移量，以及目标的宽度、高度因子，注意这些值都是相对预测特征图尺度上的，如果要映射回原图需要乘上当前特征图相对原图的步距stride。

关于如何将预测目标边界框信息转换回原图尺度可参考源码中decode_outputs函数（在源码项目中的yolox -> models -> yolo_head.py文件中）：

def decode_outputs(self, outputs, dtype):
    grids = []
    strides = []
    for (hsize, wsize), stride in zip(self.hw, self.strides):
        yv, xv = meshgrid([torch.arange(hsize), torch.arange(wsize)])
        grid = torch.stack((xv, yv), 2).view(1, -1, 2)
        grids.append(grid)
        shape = grid.shape[:2]
        strides.append(torch.full((*shape, 1), stride))

    grids = torch.cat(grids, dim=1).type(dtype)
    strides = torch.cat(strides, dim=1).type(dtype)

    outputs[..., :2] = (outputs[..., :2] + grids) * strides  # 预测目标边界框中心坐标
    outputs[..., 2:4] = torch.exp(outputs[..., 2:4]) * strides  # 预测目标边界框宽度和高度
    return outputs

---

3 损失计算

由于在网络的检测头中有Cls.分支、Reg.分支以及IoU.分支（其实是Obj.分支），所以损失由$L_{cls}$、$L_{reg}$以及$L_{obj}$这三部分组成，个人感觉如果把$L_{obj}$换成$L_{IoU}$会更合理。其中$L_{cls}$和$L_{obj}$采用的都是二值交叉熵损失（BCELoss）而$L_{reg}$采用的是IoULoss。还要注意的是，$L_{cls}$以及$L_{reg}$只计算正样本的损失，而$L_{obj}$既计算正样本也计算负样本的损失。

$$Loss=\frac{L_{cls}+\lambda L_{reg}+L_{obj}}{N_{pos}}$$
其中：

• $L_{cls}$代表分类损失
• $L_{reg}$代表定位损失
• $L_{obj}$代表obj损失
• $\lambda$代表定位损失的平衡系数，源码中设置是5.0
• $N_{pos}$代表被分为正样的Anchor Point数

---

4 正负样本匹配策略SimOTA

SimOTA是我个人认为比较难理解的部分，主要是源码看的头大。训练网络时就是通过SimOTA来进行正负样本的匹配。而SimOTA是由OTA（Optimal Transport Assignment）简化得到的，OTA也是旷视科技同年出的一篇文章，论文名称叫做《Optimal transport assignment for object detection》，有兴趣的可以自己了解一下。根据原论文中的表二，可以看到，在YOLO v3的基准上使用SimOTA后能够给AP带来2.3个点的提升。其实我这里有个疑问，这个SimOTA对于YOLO v5能够带来多少提升，如果对YOLO v5也能带来两个多点的提升那不是YOLO v5又把YOLOX给反超了？

那OTA究竟是什么呢？下面是论文中的原话：

Specifically, OTA [4] analyzes the label assignment from a global perspective and formulate the assigning procedure as an Optimal Transport (OT) problem, producing the SOTA performance among the current assigning strategies [12, 41, 36, 22, 37].

简单来说，就是将匹配正负样本的过程看成一个最优传输问题。关于最优传输理论，说实话我不太了解所以就不展开细讲，这里为了方便理解就举个简单的例子。如下图所示，假设有1到6共6个城市（图中的五角星），有2个牛奶生产基地A和B。现在要求这两个牛奶生产基地为这6个城市送牛奶，究竟怎样安排才能最小化运输成本。假设运输成本（cost）仅由距离决定，那么很明显城市1、2、3由牛奶生产基地A负责，城市4、5、6由牛奶生产基地B负责，运输成本最低。

那么在SimOTA正负样本匹配过程中，城市对应的是每个样本（对应论文中的anchor point，其实就是grid网格中的每个cell），牛奶生产基地对应的是标注好的GT Bbox，那现在的目标是怎样以最低的成本（cost）将GT分配给对应的样本。根据论文中的公式1，cost的计算公式如下，其中$\lambda$为平衡系数，代码中设置的是3.0：
$$c_{ij}=L_{ij}^{cls}+\lambda L_{ij}^{reg}$$
通过公式可以得知，成本cost由分类损失和回归损失两部分组成，并且网络预测的类别越准确cost越小，网络预测的目标边界框越准确cost越小。那么最小化cost可以理解为让网络以最小的学习成本学习到有用的知识。看到这里如果不理解也没关系，后面会有更详细的例子。

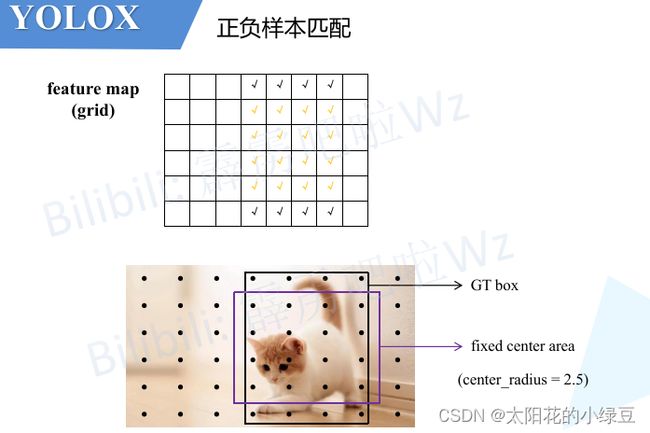
刚刚在上面有提到，城市对应的是每个样本（对应论文中的anchor point，其实就是grid网格中的每个cell），那是不是所有的样本都要参与cost的计算呢，当然不是。这里先回忆一下之前讲过的FCOS网络，它是如何匹配正负样本的？它是将那些落入GT中心sub-box范围内的样本视为正样本，其他的都视为负样本。那在SimOTA中，也有个类似的预筛选过程，通过阅读源码分析得到它首先会将落入目标GT Bbox内或落入fixed center area内的样本给筛选出来，在源码中作者将center_ratius设置为2.5，即fixed center area是一个5x5大小的box。如下图所示，feature map（或者称grid网格）中所有打勾的位置都是通过预筛选得到的样本（anchor point）。注意，这里将落入GT Bbox与fixed center area相交区域内的样本用橙色的勾表示。

接着计算网络在这些样本（anchor point）位置处的预测值（目标类别以及目标边界框）和每个GT的$L_{ij}^{cls}$以及$L_{ij}^{reg}$（由于回归损失是IoULoss，所以这里也知道每个样本和每个GT的IoU），然后再计算每个样本和每个GT之间的cost。这里需要注意下，在代码中计算cost的过程如下，和论文中给的公式有一点点区别：

cost = (
            pair_wise_cls_loss
            + 3.0 * pair_wise_ious_loss
            + 100000.0 * (~is_in_boxes_and_center)
        )

其中：

• pair_wise_cls_loss就是每个样本与每个GT之间的分类损失$L_{ij}^{cls}$
• pair_wise_ious_loss是每个样本与每个GT之间的回归损失$L_{ij}^{reg}$
• is_in_boxes_and_center代表那些落入GT Bbox与fixed center area交集内的样本，即上图中橙色勾对应的样本，然后这里进行了取反~表示不在GT Bbox与fixed center area交集内的样本（非橙色样本），即上图中黑色勾对应的样本。接着又乘以100000.0，也就是说对于GT Bbox与fixed center area交集外的样本cost加上了一个非常大的数，这样在最小化cost过程中会优先选择GT Bbox与fixed center area交集内的样本。

接下来介绍如何利用cost去进行正负样本的匹配，以下内容全部是按照源码中的计算流程进行讲解，可能没那么容易理解，如果想看懂源码的话建议多看几遍。

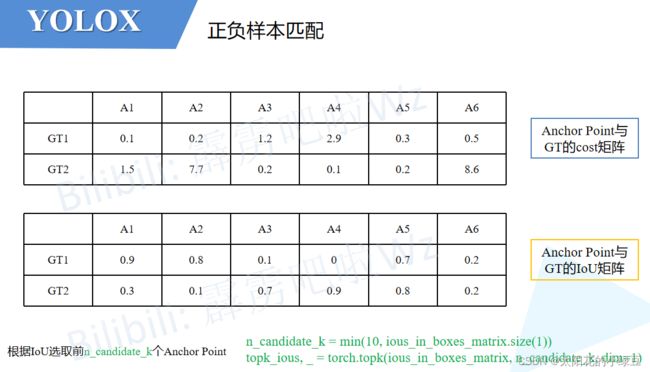
• 首先构建两个矩阵，一个是之前筛选出的Anchor Point与每个GT之间的cost矩阵，另一个是Anchor Point与每个GT之间的IoU矩阵。接着计算n_candidate_k并结合IoU对Anchor Point做进一步筛选（保留IoU大的Anchor Point），n_candidate_k是取10和Anchor Point数量之间的最小值，在下面给的这个示例中由于Anchor Point数量为6，所以n_candidate_k=6故保留所有的Anchor Point（下面示例中的值都是我随手写的，不必深究）。
  

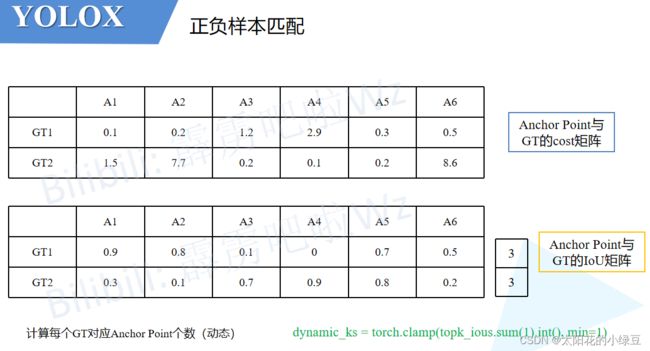
• 接着对每个GT计算剩下所有的Anchor Point的IoU之和然后向下取整得到针对每个GT所采用的正样本数量，即代码中计算得到的dynamic_ks（这个计算过程对应论文中的Dynamic k Estimation Strategy）。对于下面的示例，GT1的所有Anchor Point的IoU之和为3.0向下取整就是3所以对于GT1有3个正样本，同理GT2也有3个正样本。
  

• 然后根据刚刚计算得到的dynamic_ks（每个GT对应几个正样本）和cost矩阵找出所有的正样本（根据cost的数值大小）。比如对于示例中的GT1，刚刚计算采用3个正样本，然后看下GT1和所有Anchor Point的cost，按照从小到大的顺序将前3小的Anchor Point找出来，即示例中的A1、A2和A5。同理对于GT2，cost排前3的是A3、A4和A5。根据以上结果，我们可以再构建一个Anchor Point分配矩阵，记录每个GT对应哪些正样本，对应正样本的位置标1，其他位置标0。
  

• 按照示例我们会发现一个问题，即GT1和GT2同时分配给了A5。作者为了解决这个带有歧义的问题，又加了一个判断。如果多个GT同时分配给一个Anchor Point，那么只选cost最小的GT。在示例中，由于A5与GT2的cost小于与GT1的cost，故只将GT2分配给A5。
  
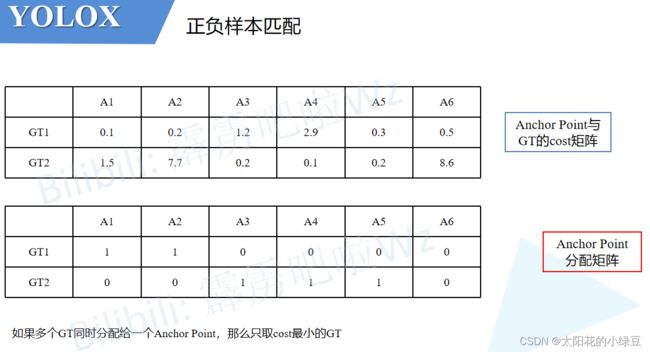
  根据以上流程就能找到所有的正样本以及正样本对应的GT了，那么剩下的Anchor Point全部归为负样本。

---

到此，有关YOLOX的内容就基本讲完了。如果觉得这篇文章对你有用，记得点赞、收藏并分享给你的小伙伴们哦。