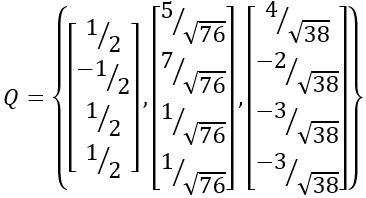矩阵的QR分解(jama和emjl对比,UJMP锦上添花)
一、QR分解法(QR Decomposition)
QR分解法是三种将矩阵分解的方式之一。其它两种:Cholesky和LU。QR分解经常用来解线性最小二乘法问题。QR分解也是特定特征值算法即QR算法的基础。
应用:
- 求解determinant,因为Q的det是1,因此只需要把R的对角乘积求出来就可以了
- 线性问题求解,这种方法比直接求逆来的更快速且数值更稳定
QR分解法(QR Decomposition)是目前求一般矩阵全部特征值的最有效并广泛应用的方法,一般矩阵先经过正交相似变化成为Hessenberg矩阵,然后再应用QR方法求特征值和特征向量。它是将矩阵分解成一个正规正交矩阵( Orthogonal Matrix )Q与上三角形矩阵R,所以称为QR分解法。
【该算法对对称矩阵和非对称矩阵都适用】
1.1施密特正交化过程(Gram–Schmidt process)
使用迭代的方法,一列一列的去掉当前列与前面的垂直部分。因为在第k步的时候已经求出了能够span前k-1列的垂直归一向量,那么在第k步的时候去掉第k列在之前k-1个基向量上面构成超平面的投影向量,再去做归一处理即可。具体可以参考维基
这个方法已经几乎被弃用,虽然逻辑清晰,但是数值不稳定。可以看到下一步的垂直向量是收到之前所有误差的累加,误差随矩阵规模(应该是线性)增加,因此数量级差的大的话会有问题。
举例:
- 寻找A的正交基(Orthogonal Basis)
随便选择一列(在这个例子中就选第一列好了),作为基准,并作为第一列的偏正交基(Partial Orthogonal Basis),以下简称PoB,记为X
- 现在偏正交基(PoB)只有一列,每一步随着我们计算其他列,X都会更新,我们同理计算其余两列:
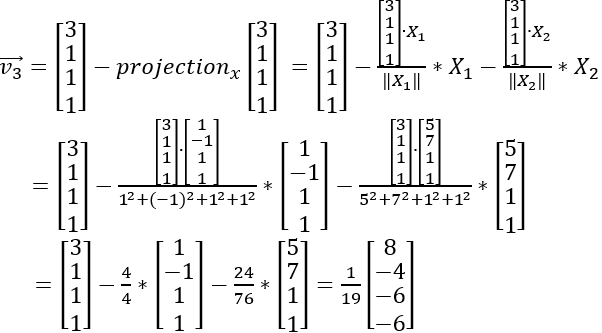
(首先需要计算第二列减去第二列在X上的投影,投影怎么算呢?用第二列跟X相对应的列点乘,然后除以X相对应的基的长度(模),再乘以X相对应的基,最后得出的偏正交基还可以约去公约数,因此现在偏正交基X变成了:)
- 计算最后一列
- 约去公约数,化成最简单状态(当然也可以不约),最终的偏正交基如下:
- 接下来我们对X标准化,得出Q,也就是说Q=Normalized(X):
- 所以
- 现在求到了Q,我们下一步需要求R
![]()
- 我们在等号两边乘以Q的转置,因为Q是正交矩阵,因此Q乘以Q的转置等于单位矩阵(Identical Matrix)则上式变成:
所以:
1.2Householder reflections(豪斯霍尔德)
巧妙构造一个orthonormal的矩阵,且这个矩阵能够QA之后去掉第一列除了第一个元素其他的数值,逐步实现一列一列消除。对于任意的向量x,使得α = x的模,于是就有这样的构造使得Q是orthonormal (可以验证QQ^T=Id)。
这种方法,误差并不会累加,可能会加加减减,保持同一数量级或者累乘(累乘的话误差越来越小,数值稳定)
【算法复杂度约为2 / 3 n^3算法稳定性也比较好, 这个算法的问题是无法并行,一次性需要的内存较多。】
1.3Given Rotation(吉文斯)
利用四角rotation矩阵,逐步去掉左下角的元素,最后将各种G累乘起来,这个算法求解路径比较复杂,而且求三角函数的反函数也会有比较大的误差和计算量,虽然巧妙但是不实用。
二、jama(通过Householder实现)
Jama是一个非常好用的Java的线性代数软件包。适用于日常编程可能碰到的各种矩阵运算问题,提供了一个优雅的简便的解决方案。官网>>>
gov.nist.math
jama
1.0.3
2.1功能
Jama由6大类组成:Matrix, CholeskyDecomposition, LUDecomposition, QRDecomposition, SingularValueDecomposition和 EigenvalueDecomposition。
Matrix类提供数值线性代数的基本运算。各种获取和设置提供对子矩阵和矩阵元素的访问。- 对称正定矩阵的Cholesky分解
CholeskyDecomposition - 矩阵的LU分解(高斯消元)
LUDecomposition - 矩阵的QR分解
QRDecomposition - 对称和非对称矩阵的特征向量值分解
EigenvalueDecomposition - 矩阵的奇异值分解
SingularValueDecomposition
2.2Matrix
2.2.1构造函数:
// 1. 从2维数组转换
Matrix(double[][] A);
// 2. 快速构造(不检查参数)
Matrix(double[][] A, int m, int n);
// 3. 从1维压缩数组构造函数
Matrix(double[] vals, int m);
// 4. 构造m*n的空矩阵(以0填充)
Matrix(int m, int n);
// 5. 构造m*n的矩阵
Matrix(int m, int n, double s);
// 6. m*n单位矩阵
Matrix.identify(int m, int n);
// 7. m*n随机矩阵
Matrix.random(int m, int n);
2.2.2方法
// 1. Matrix转换为double[][]形式
A.getArray();
// 2. 获取Matrix行数
A.gerRowDimension();
// 3. 获取Matrix列数
A.getColumnDimension();
// 4. 获取位于[i][j]的元素
A.get(i,j);
// 5.获取[i1][j1]-[i2][j2]范围内的矩阵
getMatrix(int i1, int i2, int j1, int j2);
// 举例: A为4*5的矩阵
A.getMatrix(0,4,5,5); //获取A的最后一列
// 6. 对A[i1][j1]-A[i2][j2]范围内的矩阵赋值
setMatrix(int i0, int i1, int j0, int j1, Matrix X);
// 举例: A为4*5的矩阵,B为4*2的矩阵
A.setMatrix(0,4,1,2,B); // 将B赋值到A的第2、3列
// ps: <5.><6.>中的i,j可以用数组表示
A.getMatrix(int[] r, int[] c);
A.getMatrix(int i1, int i2, int[] c);
A.getMatrix(int[] r, int j1, int j2);
A.setMatrix(int[] r, int[] c, Matrix B);
A.setMatrix(int i1, int i2, int[] c, Matrix B);
A.setMatrix(int[] r, int j1, int j2, Matrix B);
2.2.3基本运算
// 1. 加
A.plus(B); //C=A+B
A.plusEquals(B); //A=A+B
// 2. 减
A.minus(B); //C=A-B
A.minusEquals(B); //A=A-B
// 3. 乘
A.times(B); //C=A*B
A.times(s); //C=s*A
A.timesEquals(s); //A=s*A
// 4. 元素乘法
A.arrayTimes(B); //C=A.*B
A.arrayTimesEquals(B);//A=A.*B
// 5. 元素除法
A.arrayLeftDivide(B); //左除 C=A.\B
A.arrayLeftDivideEquals(B); //A=A.\B
A.arrayRightDivide(B); //右除 C=A./B
A.arrayRightDivideEquals(); //A=A./B
// 8. 转置矩阵
A.transpose();
2.2.4矩阵相关数学量
// 1. 条件数(2范式)
(double) A.cond();
// 2. 行列式
(double) A.det();
// 3. 求秩
(int) A.rank();
// 4. 求逆/伪逆
A.inverse();
2.2.5线性方程求解
// 最小二乘
A.solve(B); // A*X=B
A.solveTranspose(B); //A'*X'=B'
2.2.6矩阵分解
三、Ejml(推荐)
Efficient Java Matrix Library (EJML) 是一个线性代数库,用于处理实数/复数/密集/稀疏矩阵。它的设计目标是;1) 对小型和大型矩阵尽可能地具有计算和内存效率,以及新手和专家都可以访问。这些目标是通过动态选择在运行时使用的最佳算法、干净的 API 和多个接口来实现的。EJML 是免费的,100% 用 Java 编写,并已在 Apache v2.0 许可下发布。具有以下功能:
- 基本运算符(加法,乘法,...)
- 矩阵操作(提取、插入、组合……)
- 线性求解器(线性,最小二乘,增量,...)
- 分解(LU、QR、Cholesky、SVD、特征值,...)
- 矩阵特征(秩、对称、确定性……)
- 随机矩阵(协方差、正交、对称......)
- 不同的内部格式(行优先,块,稀疏,...)
- 图表 BLAS (Semirings)
- 单线程和并发实现
- 单元测试
- Kotlin 扩展
该库详细说明:Manual - Efficient Java Matrix Library
JavaDoc:Overview
3.1使用
org.ejml
ejml-all
0.41
3.2实现
public class App {
/**
* jama 实现QR·
*/
private static void jama(double[][] array) {
// Matrix matrix = Matrix.random(2, 2);
// double[][] array = matrix.getArray();
Matrix matrix = new Matrix(array);
// System.out.println("原矩阵");
// for (int i = 0; i < array.length; i++) {
// for (int i1 = 0; i1 < array[i].length; i1++) {
// System.out.print(array[i][i1] + " ");
// }
// System.out.println();
// }
QRDecomposition qr = matrix.qr();
Matrix h = qr.getH();
// System.out.println("H矩阵");
// double[][] hArray = h.getArray();
// for (int i = 0; i < hArray.length; i++) {
// for (int i1 = 0; i1 < hArray[i].length; i1++) {
// System.out.print(hArray[0][0]+" ");
// }
// System.out.println();
// }
Matrix q = qr.getQ();
double[][] qArray = q.getArray();
// System.out.println("Q矩阵");
// for (int i = 0; i < qArray.length; i++) {
// for (int i1 = 0; i1 < qArray[i].length; i1++) {
// System.out.print(qArray[i][i1] + " ");
// }
// System.out.println();
// }
Matrix qrR = qr.getR();
double[][] qrRArray = qrR.getArray();
// System.out.println("R矩阵");
// for (int i = 0; i < qrRArray.length; i++) {
// for (int i1 = 0; i1 < qrRArray.length; i1++) {
// System.out.print(qrRArray[i][i1] + " ");
// }
// System.out.println();
// }
}
private static void ejml(double[][] array) {
// SimpleMatrix simpleMatrix = new SimpleMatrix(array);
//QRDecompositionHouseholder_DDRB
// QRExampleSimple alg = new QRExampleSimple();
// alg.decompose(simpleMatrix);
// SimpleMatrix q = alg.getQ();
// SimpleMatrix r = alg.getR();
// System.out.println("q:");
// q.print();
DMatrixRBlock rBlock = new DMatrixRBlock(2000, 2000);
for (int i = 0; i < array.length; i++) {
for (int i1 = 0; i1 < array[i].length; i1++) {
rBlock.set(i, i1, array[i][i1]);
}
}
System.out.println("j原:");
// rBlock.print();
QRDecompositionHouseholder_DDRB ddrb = new QRDecompositionHouseholder_DDRB();
ddrb.decompose(rBlock);
DMatrixRBlock q = ddrb.getQ(null, true);
// System.out.println("Q:");
// q.print();
DMatrixRBlock r = ddrb.getR(null, false);
// System.out.println("R:");
// r.print();
}
public static void main(String[] args) {
// DateTimeFormatter dtf = DateTimeFormatter.ofPattern("yyyy-MM-dd HH:mm:ss");
// String time = dtf.format(LocalDateTime.now());
//System.out.println("jama开始:" + LocalDateTime.now());
// while (i<2){
Matrix matrix = Matrix.random(2000, 2000);
double[][] array = matrix.getArray();
// jama(array);
// }
// String time1 = dtf.format(LocalDateTime.now());
System.out.println("jama结束:" + LocalDateTime.now());
// String time2 = dtf.format(LocalDateTime.now());
System.out.println("ejml开始:" + LocalDateTime.now());
ejml(array);
// String time3 = dtf.format(LocalDateTime.now());
System.out.println("ejml结束:" + LocalDateTime.now());
}
}四、结果
所以,QR分解推荐用ejml。
五、锦上添花
不管是jama还是ejml,对于矩阵的操作最复杂的程度只到log函数和exp函数,针对sin、cos等函数没有实现,如果我们自己去实现,将大大降低运行效率,所以,应该引进ujmp包,达到锦上添花的效果。