数字图像处理-形态学图像处理

腐蚀和膨胀

膨胀

膨胀是在二值图像中“加长”或“变粗”的操作。
IPT中函数imdilate执行膨胀运算，语法为
A2 = imdilate(A,B)
其中A2和A都是二值图像，B是指定结构元素的由0和1构成的矩阵。

结构元素的分解

膨胀满足交换律和结合律。假设一个结构元素B可以表示为B₁和B₂的膨胀，则A被B膨胀也可以表示为A被B₁膨胀后再被B₂膨胀。
我们称B能够分解成B₁和B₂两个结构元素。
计算膨胀所需要的时间正比于结构元素中的非零像素的个数。
利用性质，将结构元素分解为小块，可以大大节省时间

函数strel

IPT中strel函数可以构建各种形状和大小的结构元素。
se = strel(shape, parameters)

strel函数的另一个重要属性是，它能以分解的形式来产生结构元素，而函数imdilate则自动地使用分解信息来加快膨胀处理。

腐蚀

腐蚀“收缩”或“细化”二值图像中的对象。腐蚀的过程也由结构元素控制。
结构元素与像素完全匹配输出1
A被B腐蚀是所有结构元素的原点位置的集合
腐蚀使用IPT中的imerode函数实现，用法同膨胀函数imdilate。

腐蚀与膨胀的组合

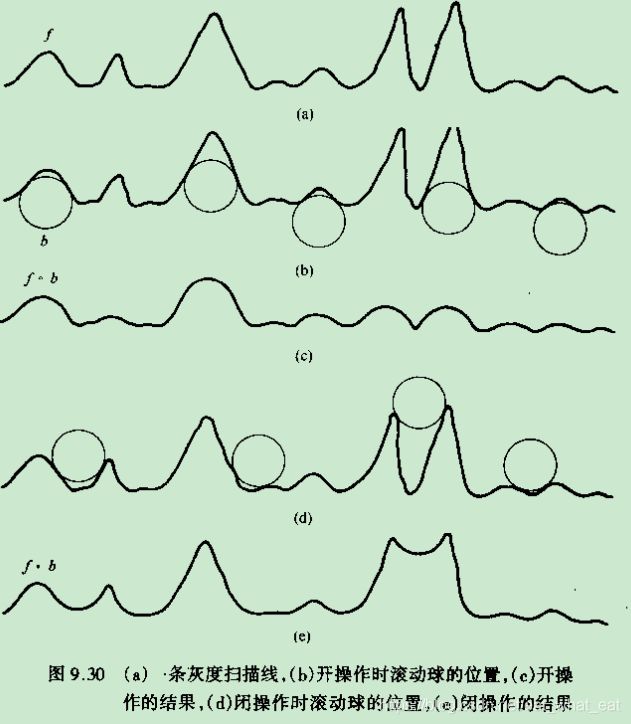
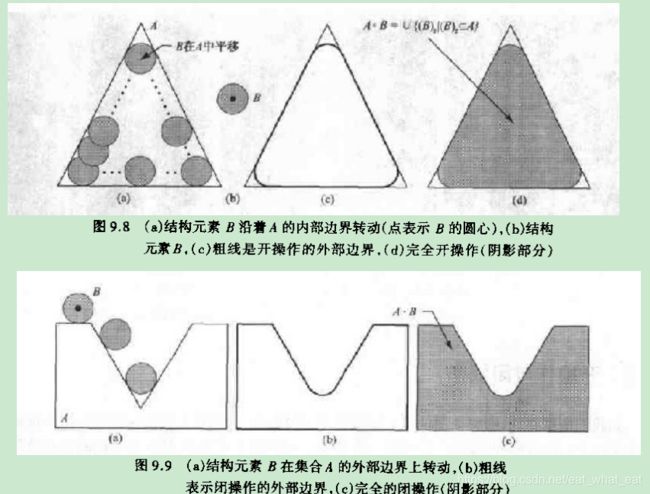
开运算和闭运算

这种运算是A先被B腐蚀后再被B膨胀。
简单集合解释为：B在A内完全匹配的平移的并集。
形态学开运算完全删除了不能包含结构元素的对象区域，平滑了对象的轮廓，去掉了细小的突出部分。

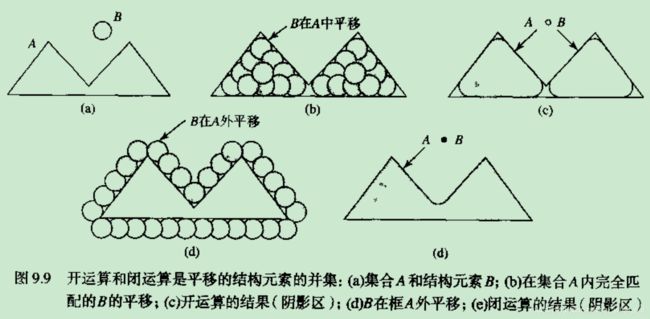
形态学闭运算是先膨胀再腐蚀。几何学解释为：所有不与A重叠的B的平移的并集。与开运算不同的是，闭运算一般会将狭窄的缺口连接起来形成细长的弯口，并填充比结构元素小的洞

开运算和闭运算再工具箱中用函数imopen和imclose实现
C = imopen / imclose(A,B)
其中A是一幅二值图像，而B是一个矩阵，这里我们使用strel函数生成的结构元素。
这副指纹图片存在一些杂点，使用开运算使其消除，但是这又在纹脊处引入了许多缺口，这时再使用闭运算填充。

击中或击不中变换

击中或击不中变换可以识别像素的特定形状，如孤立的前景像素或者是线段的端点像素。

特别地，它找到了那些邻域与第一个结构元素B1的形状匹配的像素，同时又与第二个结构元素B2的形状不匹配。

这里有例子
另一个例子

使用查找表

当击中或击不中结构元素较小时，计算击中击不中变换的较快方法是使用查找表(LUT)。这种方法是预先计算出每个可能邻域形状的像素值，然后把这些值存到一个表中，以备以后使用。
工具箱提供两个函数makelut和applylut，以此实现这种技术。
makelut基于一个提供给用户的函数构造一个查找表（不理解），applylut则使用这个表来查找处理二值图像。

一些基本形态学算法

提取边界

A的边界表示为β(A)，它可以通过先由B对A腐蚀，再用A减去腐蚀后的图像得到。若B为3* 3的结构元素可以得到宽度为一个像素的边界，若为5*5，边界宽度为2到3个像素

区域填充

图例

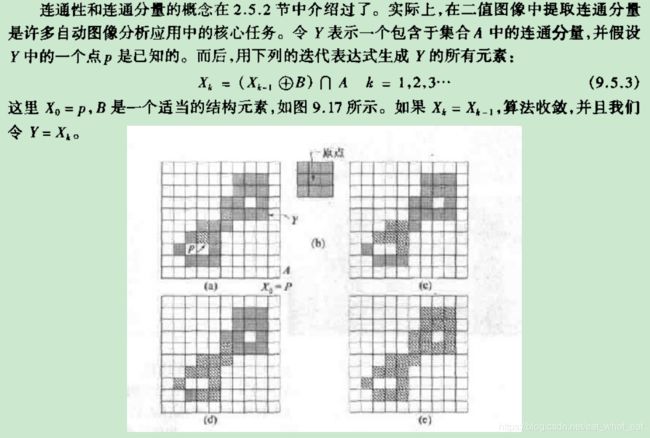
连通分量的提取

补充一个知识
四连通与八连通

凸壳

如果连接集合A内任意两个点的直线段都在A的内部，就称A是凸形的。任意集合S的凸壳H是包含S的最小凸集合。集合差H-S称为S的凸缺。

对A用B₁反复使用Hit-Miss变换，直到结果收敛，将其保存在D₁
使用B₂重复该过程。最终得到n个D集合，求它们的并集，即是A的凸壳。
P437

细化与粗化

使用结构元素B对A做Hit-Miss变换，并求其补集，再求与A的并集，即是对A的细化处理。
粗化在形态学上是与细化对偶的过程，A的粗化过程为使用B对A做Hit-Miss变换，再求变换结果与A的并集。
P438

函数bwlabel可以用于计算一幅二值图像中的所有连接分量
[L, num] = bwlabel(f,conn)
其中f是一幅输入二值图像。conn用于指定期望的连接(4或8)。输出L称为标记矩阵，在相应的像素点标记出它属于第几个区域，参数num给出所找到的连接分量的数量。若省略参数conn，则连接数为8.

形态学重构

重构是一种涉及到两幅图像和一个结构元素(而不是单幅图像和一个结构元素)的形态学变换。一幅图像，即标记(maker)，是变换的开始；另一幅图像时掩模(mask)，用来约束变换过程；结构元素用于定义连接性。若g是掩模，f是标记，则从f重构g可以记为R_g(f),他的过程是：
1.将h₁初始化为标记图像f
2.创建结构元素B = ones(3)
3.重复，将h_k和B的膨胀结果与g取交集，并将结果赋予h_k+1
直到 h_k+1 = h_k
标记 f 必须是g的一个子集

IPT中提供的是快速混合重构算法imreconstruct
out = imreconstruct(maker, mask)

由重构做开运算

在形态学开运算中，腐蚀通常会去除小的对象，而随后的膨胀往往会还原所保留对象的形状。然而，这种还原的精度取决于形状和结构元素之间的相似性。由重构做开运算将准确地恢复腐蚀之后的对象形状。

填充孔洞

灰度级图像扩展

膨胀和腐蚀

通常对灰度图像进行膨胀处理的结果是双重的:(1)如果所有的结构元素的值都为正，则输出的图像会趋向于比输入图像更亮；(2)暗的细节部分全部减少了还是消除了取决于膨胀所用的结构元的值和形状
膨胀示意图
对灰度图像进行腐蚀的结果也是双重的：(1)如果所有的结构元素都为正，输出图像会趋向于比输入图像更暗；(2)在输入图像中亮的细节的面积如果比结构元素的面积小，则亮的效果将被消弱。消弱的程度取决于环绕于亮的细节周围的灰度值和结构元素自身的形状与赋值。

腐蚀和膨胀可以组合使用，以获得各种效果。例如，从膨胀后的图像减去腐蚀过的图像可以产生一个“形态学梯度”，它是检测图像中局部灰度级变换的一种度量。 形态学梯度使输入图像中灰度级的跃变更为急剧。使用对称结构元素得到的形态学梯度对边缘方向性的依赖更小。

>> g = imread(\alcatraz1.jpg');
>> f = rgb2gray(g);彩色图像转灰度图像
>> se = strel('square',3);结构元素
>> gd = imdilate(f,se);膨胀
>> ge = imerode(f,se);腐蚀
>> morph_grad = imsubtract(gd,ge);求梯度

开运算和闭运算

形态学平滑

由于开运算可以去除比结构元素更小的明亮细节，闭运算可以去除比结构元素更小的暗色细节，所以它们经常组合在一起用来平滑图像并去除噪声。

>> f = imread('123.jpg');
>> se = strel('disk',5);
>> fo = imopen(f,se);
>> foc = imclose(fo,se);

此过程中对图像背景和细节都做了平滑处理。
上述过程通常称为开-闭滤波，闭-开滤波可以产生类似的效果。

另一种组合使用开运算和闭运算的方法是交替顺序滤波。交替顺序滤波的一种形式是用一系列不断增大的结构元素来执行开-闭滤波。

>> fasf = f;
>> for k = 2:5
        se = strel('disk', k);
        fasf = imclose(imopen(fasf,se), se);
   end

顶帽变换

开运算可以补偿不均匀的背景亮度。方法是使用大于前景元素的结构元素，对图像进行开运算，再使用原图像减去该图像，可以得到一幅具有合适且均匀的背景的图像。
从原图像减去开运算后的图像称为顶帽(top-hat)变换。IPT中使用函数imtophot即可完成该操作
fe = imtophat(f, se);
与之相关的函数还有imbothat，它可以执行底帽(bottom-hat)变换，这种变换定义图像减去经闭运算后的图像。语法同imtophat。这两个函数可以一起用于增强对比度。

>> se = strel('disk', 5);
>> q = imsubtract(imadd(f, imtophat(f, se)), imbothat(f, se));

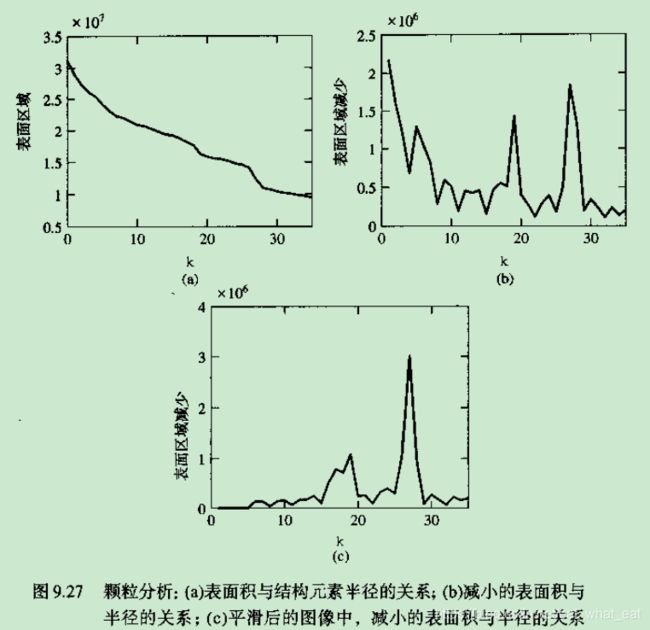
颗粒分析

确定一幅图像中的颗粒大小分布是颗粒分析技术领域的重要组成部分。形态学技术可以间接地度量颗粒的大小分布，换言之，不能准确地识别并度量每一个颗粒。对于形规则且亮于背景的颗粒，基本方法是应用不断增大尺寸的形态学开运算。对于每个开运算，开运算中的所有像素值的和会被计算，该和有时称为图像的表面积。