单细胞数据分析工具scvi介绍
之前听师兄在组会上介绍了scvi,恰巧最近在用scvi做一些分析,感觉这个方法很精巧效果也不错,因此研究了一下原始论文,这里简要介绍一下这个单细胞数据分析工具的新星。
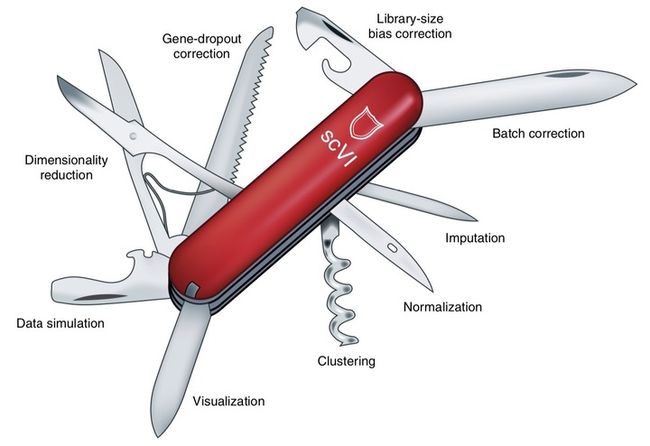
scvi是Nature Methods在2018年12月发表的一个单细胞RNA测序(scRNA-seq)数据的集成分析平台,预印版文章在2018年3月就已经在bioRxiv上线。scvi是一个快速的多功能方法,整合了来自机器学习、统计模型、概率图模型等领域的思想和模型,应用到了单细胞数据的多种下游分析上来,相比其他针对单一下游分析的方法来说,从生物信息学的角度来讲是一个很大的进步。同期的Nature Methods期刊上也发表了一篇News来介绍这个工作,里面用一个瑞士军刀的比喻来说明scvi功能的全面。
瑞士军刀的比喻,非常形象,图片来自原文
问题背景
单细胞测序数据将人们对生物特性的认知细化到了细胞层面,极大地促进了生物发现的进程。但是这种“高分辨率”的信息捕获技术也有着自身的局限性,比如测量灵敏度的不确定性,批次效应(batch effect,指即便是同一种细胞同一测序技术不同次的测序结果也存在着偏差),还有技术本身带来的噪声等等,进而影响了基于单细胞测序技术的下游分析的质量,比如细胞聚类(可以找到一组细胞中的常见子类,并发现新的子类或者亚群)、基因差异表达(找到不同细胞群之间表达量显著差异的基因)、轨迹分析(trajectory analysis,研究细胞发展变化的过程)等等。
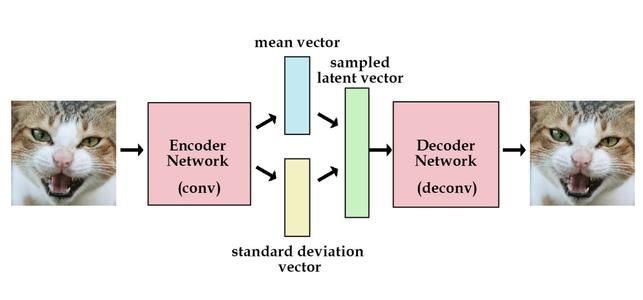
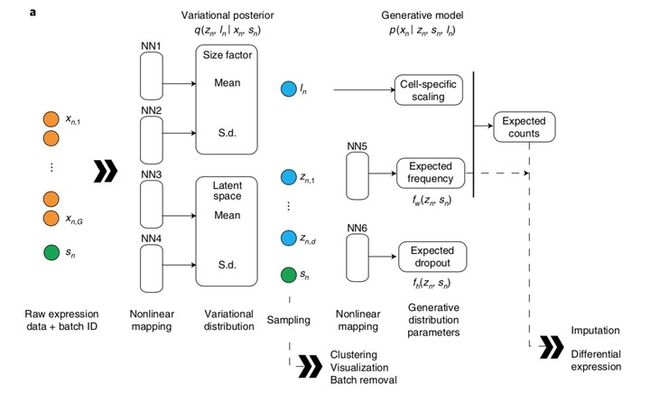
scvi提出了基于深度神经网络的层次贝叶斯模型 (Hierarchical Bayesian Model) 来解决这些问题,其中贝叶斯模型中的条件概率由神经网络来实现。这是一个生成式模型,模型结构如下图所示,将scRNA-seq数据中每个细胞作为一个样本,其基因表达作为特征,通过encoder的神经网络与重参数化将高维的基因表示压缩到低维隐空间(比如说10维);之后基于单细胞RNA测序数据基因表达量服从零膨胀负二项分布 (ZINB) 的假设(相关内容可以参考我的另一篇总结),再利用decoder的神经网络将隐空间映射到基因表达分布参数的后验估计上。scvi的两大优势在于:
-
模型考虑了scRNA-seq数据中的两大问题:library size 和 batch effect
-
利用单一生成式模型为一系列的下游分析提供了数据基础
scvi模型结构,图片来自原文
模型介绍
我们从变分的角度来整体理解scvi模型。首先明确输入数据和隐变量,输入包括两部分,一部分是细胞 n 的基因表示 ![]() 到
到 ![]() (一共G个基因,一般是几万维),另一部分是细胞 n 的batch信息
(一共G个基因,一般是几万维),另一部分是细胞 n 的batch信息 ![]() ;隐变量为
;隐变量为 ![]() 和
和 ![]() ,
, ![]() 是一个一维变量,表示数据的“尺度” (scale),
是一个一维变量,表示数据的“尺度” (scale), ![]() 是一个低维向量(scvi取10维),是数据维度压缩后的表示。
是一个低维向量(scvi取10维),是数据维度压缩后的表示。
在推断隐变量 ![]() 和
和 ![]() 的后验分布中,作者引入了变分推断的思想,即原始分布 P(X) 不好求解时,考虑引入一个简单的分布 Q(X) 来近似,利用KL散度(或者其他度量,KL是最常用的)来度量两个分布之间的距离,并希望最小化这个距离。在单细胞数据的建模中,这一距离及其展开如下:
的后验分布中,作者引入了变分推断的思想,即原始分布 P(X) 不好求解时,考虑引入一个简单的分布 Q(X) 来近似,利用KL散度(或者其他度量,KL是最常用的)来度量两个分布之间的距离,并希望最小化这个距离。在单细胞数据的建模中,这一距离及其展开如下:
移项可得:
![]()
上式中第一项是对数似然函数,第二项(不带符号)是我们要最小化的KL散度,根据定义恒为正,由于给定数据后似然函数不变,因此最小化第二项的KL散度就等价于最大化等号右侧的两项之和,因此优化目标可以表示为下面不等式的右侧,也就是变分推断中的Evidence Lower Bound (ELBO):
![]()
在scvi中对于近似分布Q采用mean-field(简单来说就是所有变量独立,具体可以参考概率图模型相关资料),因此对于隐变量 z 和 l 来说是独立的,上面的不等式就可以改写为:
![]()
注意到数据的对数似然分布其实和batch信息 s 无关,可以看做是每个batch(注意这里batch是一组单细胞数据,和机器学习里的batch不是一回事)下的基因表达值,是一种条件表示,因此可以将 P(x,s) 写成 P(x|s) ,上面的不等式变为:
![]()
经过上面的一番推导我们终于得到了原文在Methods章节给出的不等式,这也是我们训练的优化目标函数,注意这里为了书写方便我们去掉了下标 n 。现在我们来看ELBO这三项的具体内容。对于隐变量 ![]() ,它是从一个对数正态分布中生成的,分布的参数由第一组变换网络(scvi方法图中的NN1,NN2,分别对应生成均值和方差)决定:
,它是从一个对数正态分布中生成的,分布的参数由第一组变换网络(scvi方法图中的NN1,NN2,分别对应生成均值和方差)决定:
![]()
对于隐变量 ![]() ,每一个元素是从正态分布中生成的,分布的参数由第二组变换网络(scvi方法图中的NN3,NN4,分别对应生成均值和方差)决定:
,每一个元素是从正态分布中生成的,分布的参数由第二组变换网络(scvi方法图中的NN3,NN4,分别对应生成均值和方差)决定:
![]()
在Q分布中,scvi的假设是 ![]() 服从参数
服从参数 ![]() 的对数正态分布,两个参数对应训练数据每个batch(这里batch才是机器学习中批的概念)中数据的均值和方差;
的对数正态分布,两个参数对应训练数据每个batch(这里batch才是机器学习中批的概念)中数据的均值和方差; ![]() 服从标准正态分布,因此对应的KL散度可以写为:
服从标准正态分布,因此对应的KL散度可以写为:
![]()
![]()
接下来看剩下的一项 ![]() ,这里面包含了由隐空间生成 x 的重构表示的过程,scvi巧妙地定义了下面的变量决定关系,将ZINB分布融合进这一过程中:
,这里面包含了由隐空间生成 x 的重构表示的过程,scvi巧妙地定义了下面的变量决定关系,将ZINB分布融合进这一过程中:
![]()
![]()
![]()
![]()
![]()
![]()
其中 ![]() 和
和 ![]() 是神经网络(scvi方法图中的NN5,NN6),将隐变量
是神经网络(scvi方法图中的NN5,NN6),将隐变量 ![]() 映射回基因表达的原始高维空间上,并分别参与重构基因表达值(
映射回基因表达的原始高维空间上,并分别参与重构基因表达值(![]() )和表达值丢失(dropout现象)的判断 (
)和表达值丢失(dropout现象)的判断 (![]() ),值得注意的是
),值得注意的是 ![]() 在基因差异表达中扮演了重要角色,此处不展开说明了,可以查看原文。
在基因差异表达中扮演了重要角色,此处不展开说明了,可以查看原文。 ![]() 是一个G维向量,用来表征每个基因的dispersion(NB分布的参数),需要注意的是Gamma-Poisson就是NB分布,这些可以参看我之前的文章,里面有说明。因此通过神经网络的映射和计算可以得到重构后的每个基因在该细胞中的表达值。进而可以计算:
是一个G维向量,用来表征每个基因的dispersion(NB分布的参数),需要注意的是Gamma-Poisson就是NB分布,这些可以参看我之前的文章,里面有说明。因此通过神经网络的映射和计算可以得到重构后的每个基因在该细胞中的表达值。进而可以计算:
注意以上的变量 ![]() 都是向量形式,为了简洁表述基本思想没有加粗。到此我们给出了整个网络的训练损失函数:
都是向量形式,为了简洁表述基本思想没有加粗。到此我们给出了整个网络的训练损失函数:
scvi的网络基本还是一个VAE的结构(如下图),只是在encoder中scvi将原始数据变换到两个隐空间并分别进行重参数化,进而生成了不同的隐层表示 ![]() 和
和 ![]() ;在decoder中并不是直接将生成的隐空间表示利用神经网络映射回输入的
;在decoder中并不是直接将生成的隐空间表示利用神经网络映射回输入的 ![]() ,而是由神经网络映射到ZINB的参数或者对应超参数,之后利用ZINB模型采样得到重构后去噪的基因表达值
,而是由神经网络映射到ZINB的参数或者对应超参数,之后利用ZINB模型采样得到重构后去噪的基因表达值 ![]() .
.
VAE示意图,图片来自百度
此外,根据文章中所述,scvi的每个子神经网络(即方法图中的"NNx")都只有1~3个隐层组成,每层128或者256个节点,训练时迭代120~250个epoch即可。由于scvi是基于PyTorch完成的,因此可以在GPU上训练,非常机器学习友好!需要注意我一直都说“机器学习”是因为我觉得scvi的网络太浅了,不太能算作深度学习的范畴(虽然原文作者说他们是deep neural network),但恰恰因为网络浅所以训练速度快。另一个scvi的巨大优势是可以同时跑很多的细胞数据(百万级),这在高通量测序时代是非常必要的。
模型应用与性能
此处应该重新回顾scvi方法图,里面注明了下游分析应用方向和所用的数据(取隐层表示 ![]() 还是重构表示
还是重构表示 ![]() )。隐层表示可以用来聚类、可视化(毕竟维数低)和去批次效应;重构表达量可以作为imputation的结果,并用于基因差异表达分析。由于本文主要是方法说明与解释,scvi具体应用效果这里就不贴了,感兴趣的朋友可以查看原文。
)。隐层表示可以用来聚类、可视化(毕竟维数低)和去批次效应;重构表达量可以作为imputation的结果,并用于基因差异表达分析。由于本文主要是方法说明与解释,scvi具体应用效果这里就不贴了,感兴趣的朋友可以查看原文。
下面是我用scvi在两个10x的PBMC 5k数据上做的去批次效应实验,两组数据使用的建库方法不同,虽然方法详情我也不懂,但确实是很好的带批次效应的数据。scvi处理的结果不错,当然还是要感谢原文作者提供的Tutorial:
https://github.com/YosefLab/scVIgithub.com
读入原始数据与简单预处理
# Library
from scvi.dataset
import Dataset10X, GeneExpressionDataset
import numpy as np
from scvi.models import VAE
# Data Loading, including data using techniques "v3" & "next" save_path = "." # Please specify by yourself
data_v3 = Dataset10X(save_path=save_path+"/pbmc_5k/filtered_feature_bc_matrix/", measurement_names_column=1, dense=True )
print(data_v3.X.shape) data_next = Dataset10X( save_path=save_path+"/pbmc_5k/filtered_feature_bc_matrix_next/", measurement_names_column=1, dense=True )
print(data_next.X.shape)
# Basic data filtering, removing non-expressed genes and non-detected cells data_v3.filter_genes_by_count(min_count=1) data_v3.filter_cells_by_count(min_count=1)
print(data_v3.X.shape)
data_next.filter_genes_by_count(min_count=1) data_next.filter_cells_by_count(min_count=1)
print(data_next.X.shape)
# Data merge
data_all = GeneExpressionDataset()
data_all.populate_from_datasets([data_v3, data_next])
print(data_all.X.shape)
训练,使用GPU
# Training
n_epochs = 200
lr = 1e-3
use_batches = True
use_cuda = True
test_mode = False
vae = VAE(data_all.nb_genes, n_batch=data_all.n_batches * use_batches)
trainer = UnsupervisedTrainer(vae, data_all, train_size=0.9 if not test_mode else 0.5, use_cuda=use_cuda, frequency=10, )
trainer.train(n_epochs=n_epochs, lr=lr)获得隐层表示与重构output
# Obtain latent variables and reconstructed outputs
full = trainer.create_posterior(trainer.model, data_all, indices=np.arange(len(data_all)))
print("Entropy of batch mixing :", full.entropy_batch_mixing())
latent, batch_indices, labels = full.sequential().get_latent()
normalized_values = full.sequential().get_sample_scale()可视化展示
# Visualization by scannpy using Umap
import scanpy as sc
import anndata
post_adata = anndata.AnnData(X=data_all.X)
sc.pp.normalize_total(post_adata, target_sum=1e4)
sc.pp.log1p(post_adata)
sc.pp.scale(post_adata, max_value=10)
post_adata.obsm["original"] = post_adata.data
post_adata.obsm["imputed"] = normalized_values
post_adata.obsm["X_scVI"] = latent
post_adata.obs['cell_type'] = np.array([data_all.cell_types[data_all.labels[i][0]] for i in range(post_adata.n_obs)])
post_adata.obs['batch'] = np.array([str(data_all.batch_indices[i][0]) for i in range(post_adata.n_obs)])原始数据结果(经过normalize和scale,见上面代码)
# Original Umap
sc.pp.neighbors(post_adata, use_rep="original", n_neighbors=15)
sc.tl.umap(post_adata)
fig, ax = plt.subplots(figsize=(7, 6))
sc.pl.umap(post_adata, color=["batch"], ax=ax, show=True)
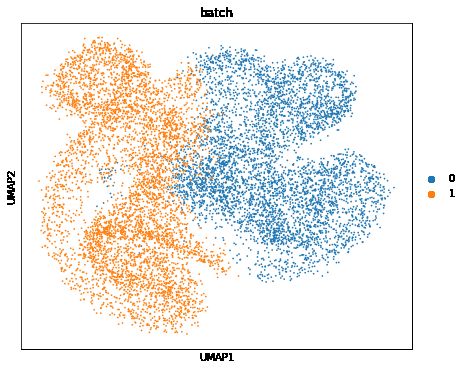
原始数据的Umap,批次效应是很严重的
使用隐层表示的结果
# Latent Umap
sc.pp.neighbors(post_adata, use_rep="X_scVI", n_neighbors=15)
sc.tl.umap(post_adata)
fig, ax = plt.subplots(figsize=(7, 6))
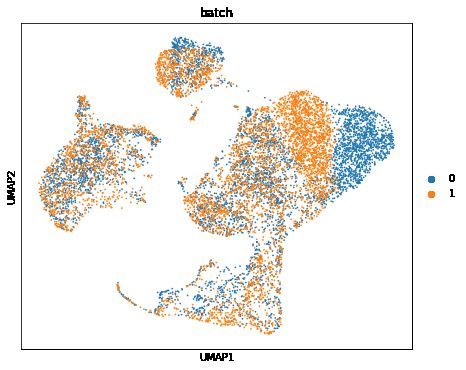
sc.pl.umap(post_adata, color=["batch"], ax=ax, show=True)使用latent variable的Umap,可以看到批次效应几乎消除了
使用重构输出的基因表达数据(imputation)的结果
# Imputation Umap
sc.pp.neighbors(post_adata, use_rep="imputed", n_neighbors=15) sc.tl.umap(post_adata)
fig, ax = plt.subplots(figsize=(7, 6))
sc.pl.umap(post_adata, color=["batch"], ax=ax, show=True)
使用imputation的数据的去batch结果,效果就不那么好了(右侧)
在1080Ti的GPU上,10k个细胞跑了200个epoch接近三分半,速度还可以。
另外开发scvi的lab还做了整合蛋白质数据(比如CITE-seq)的集成分析工具totalVI,以及整合空间转录组的分析数据gimVI,都有bioRxiv版本,还没有研究,感兴趣的朋友可以看一下。另外欢迎大家交流scvi或者其他单细胞数据分析方法(比如Seurat)的使用心得,感觉对应的中文资料太少了,全靠经验和摸索。
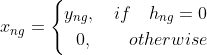
![E_{z,l\sim Q}[logP(x|s,z,l)]=\frac{1}{M}\sum_{i}^{M}\sum_{g}^{G}{logP(x_{ng}|z^i_n,l_n,s_n)}](http://img.e-com-net.com/image/info8/356c2f58ab9d47cd9b593c1c44fcc477.gif)
![loss=\frac{1}{M}\sum_{i}^{M}\sum_{g}^{G}{logP(x_{ng}|z^i_n,l_n,s_n)}+ D[logN(\mu_{l_n},\sigma^2_{l_n})||logN(l_\mu,{l_\sigma}^2)]+D[N(\mu_{z_n},\sigma^2_{z_n})||N(0,I)]](http://img.e-com-net.com/image/info8/d33a58a5551d41b4a999c3591a9190b2.gif)