自编Matlab代码实现MPC定点跟踪

自编Matlab代码实现MPC（线性）定点跟踪

这篇文章是在上一篇的基础上进一步对自编的MPC-Matlab代码进行了一定程度的延伸，主要是增加了定点跟踪功能，以及将每一步的预测状态量与控制量作图的功能。

一、模型准备及条件设置

仿真模型依然采用上一篇文章中的线性模型，但是取消了对状态量的约束（因为我不确定哪一种约束方式才是正常的，硬约束或者是间接约束），初始状态为$x_0=[-1;0]$，跟踪值设为$x_d=[5;1]$，目标函数的形式以及参数矩阵不变，预测步长为$N_p=5$。

实现误差反馈跟踪与上一篇的原理一样，主要区别就是将状态量与目标值作差，对误差值进行控制归零即可。

二、代码

clear; clc; close all;
% 线性系统系数矩阵
A=[1 1; 0 1]; B=[1; 0.5];
% 初始状态量-如果不能在下一步回到约束范围内，则会造成无解
x0=[-1; 0];
% 预测步长
Np=5;
% 优化目标参数，加权矩阵
Q=1*eye(2); R=1;
% 转化为用控制量ut表示的，关于状态量的推导方程的矩阵
At=[]; Bt=[]; temp=[];
% 转换后的加权矩阵
Qt=[]; Rt=[];

% 加权矩阵的计算过程，以及推导方程矩阵的叠加过程
for i=1:Np
        At=[At; A^i];
        Bt=[Bt zeros(size(Bt,1), size(B,2));
            A^(i-1)*B temp];
        temp=[A^(i-1)*B temp];
        
        Qt=[Qt zeros(size(Qt,1),size(Q,1));
            zeros(size(Q,1),size(Qt,1)) Q];
        Rt=[Rt zeros(size(Rt,1),size(R,1));
            zeros(size(R,1),size(Rt,1)) R];
end
% 参考输入
% xd=10*ones(1, 2*Np);
xd=[5;1];
% 控制量ut的上下限
lb=-1*ones(Np,1);
ub=1*ones(Np,1);
% 控制量ut的初始值
u0=zeros(Np,1);
% 转换后的优化目标函数矩阵，循环优化函数中H后的表达式为优化目标的另一项
H=2*(Bt'*Qt*Bt + Rt);
% 转换后的优化中的不等式约束左边系数矩阵，后面循环中的bi为不等式右边
% Ai=[Bt; -Bt];
% 声明u来保存每一步采用的控制量
u=[];
% 误差反馈
xe=x0-xd;
x=xe; %用来计算和保存误差状态量
xxe=xe; % 用来保存误差值
xx=x0; % 用来显示最后的真实状态量
figure();

for k=1:20
    
    % 关于ut的不等式约束，实际上约束的是状态量，常数4就是状态量约束的上下边界
%     bi=[5-At*xe; 5+At*xe];
    % 一切准备就绪，进行二次优化
    [ut, fval, exitflag]=quadprog(H,(2*xe'*At'*Qt*Bt)',[],[],[],[],lb,ub,u0);
    % 显示求解结果是否正常
    fprintf('%d\n', exitflag)
%     xt = At*xk + Bt*ut;
%     
%     plot(xt');
%     hold on;
    xp=[]; %xp用来记录每个time step上对未来的预测状态量
    xp_0=xe; %第一个值为当前状态量
    xp=xp_0;
    for j=1:Np
        
        xp(:, j+1) = A*xp(:, j) + B*ut(j);
        
    end
% 对每一次预测的状态量作图
    tp=k:(k+Np);
    tpu=k:(k+Np-1);
 
    subplot(2, 1, 1);
    plot(tp,xp','linewidth',1.5);
    hold on;
    subplot(2, 1, 2);
    plot(tpu, ut, 'linewidth', 1.5);
    hold on;
    
    % 采用优化得到的控制量的第一个元素作为实际作用的控制量，代入到原系统中得到下一个时刻的状态量
    u(k) = ut(1);
    x(:, k+1) = A*x(:, k) + B*u(k);
    xe = x(:, k+1);
    xxe=[xxe, xe];
    xx=[xx, xe+xd];
    % 对优化初始值进行修改，采用预测值的后段作为下一步的初始值
    u0 = [ut(2:Np); ut(Np)];
    
end
% 计算x状态值的绝对值之和，作为衡量控制效果的指标
count=sum(abs(xxe'))

figure();
subplot(2,1,1);
plot(xx','linewidth',1.5); grid on;
legend('x_1','x_2'); title('states');

subplot(2,1,2);
plot(u,'linewidth',1.5); grid on;
legend('u'); title('inputs');

以上就是全部代码，与前一篇相比差别不大，各位可以对照看看。

三、仿真结果分析

直接上图，首先是新增加的每一步预测图：

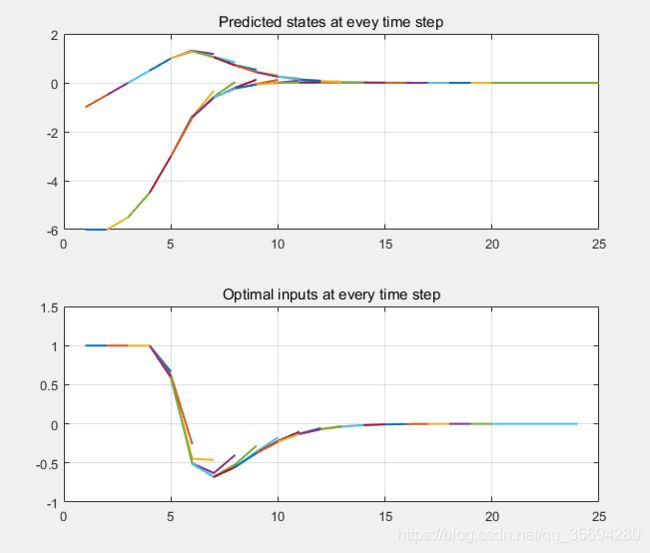
第一格为状态量，第二格为控制量。绘图的原理就是在每一步将MPC控制器所作出的预测（包括状态量与控制量）绘制下来，然后一个循环在此基础上继续重叠绘制。观察图形发现，MPC在每一个时间点做出的预测大致上与下一步的预测值重合，表明控制器做出的预测大致上符合实际状态量的走向。如果将预测步长$N_p$设置的足够大，可以发现上图中所有的曲线都将完全重合。另外，这个图中绘制的是误差值，所以最后归零表示跟踪目标成功。

然后是实际的状态量与控制量：

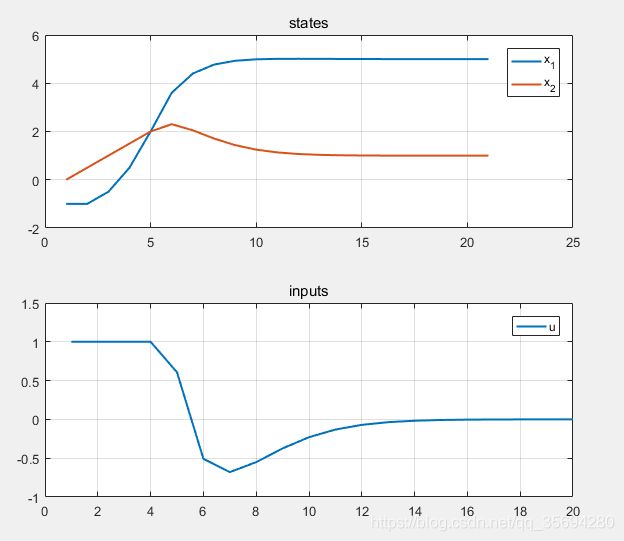
观察上图，与图1比较可以发现曲线的走势基本上相同，系统状态量也成功跟踪上了目标。到此为止就完成了定点跟踪的任务。至于轨迹跟踪或者变参考跟踪则需要进一步的修改与探索。同样的，如果大家感兴趣也可以在这个代码的基础上进行修改，比如将模型进行替换，更改预测步长，或者每一步采取预测控制量的前几位而不只是第一位等等。

如果有什么问题欢迎大家留言讨论。如果有朋友对MPC很感兴趣也欢迎私信深入讨论，共同学习进步。