基于自适应调整权重和搜索策略的鲸鱼优化算法
文章目录
- 一、理论基础
-
- 1、鲸鱼优化算法
- 2、鲸鱼优化算法的改进
-
- (1)自适应调整权重
- (2)自适应调整搜索策略
- (3)AWOA流程图
- 二、仿真对比与分析
- 三、参考文献
一、理论基础
1、鲸鱼优化算法
请参考这里。
2、鲸鱼优化算法的改进
(1)自适应调整权重
由于WOA在优化求解的过程中,线性的惯性权重调整策略若选择不合适,将影响算法的收敛速度。因此,本文提出了一种根据当前鲸鱼种群分布情况来自适应改变权值的大小,公式如下: w = d 1 ⋅ ( P i worst − P i best ) + d 2 ⋅ ( x i upper − x i lower ) / n g (1) w=d_1\cdot(P_{i\text{worst}}-P_{i\text{best}})+d_2\cdot(x_i^{\text{upper}}-x_i^{\text{lower}})/n_g\tag{1} w=d1⋅(Piworst−Pibest)+d2⋅(xiupper−xilower)/ng(1)其中, n g n_g ng表示当前种群的迭代次数; x i upper x_i^{\text{upper}} xiupper和 x i lower x_i^{\text{lower}} xilower分别为变量 x i x_i xi的上界和下界; P i worst P_{i\text{worst}} Piworst和 P i best P_{i\text{best}} Pibest分别为当前鲸鱼种群中最差鲸鱼的位置向量和最优鲸鱼的位置向量; d 1 d_1 d1和 d 2 d_2 d2是两个常数。因此,当前鲸鱼个体自适应调整权重收缩包围更新位置和自适应调整权重螺旋更新位置公式如下: X ( t + 1 ) = w ⋅ X ∗ ( t ) − A ⋅ D (2) X(t+1)=w\cdot X^*(t)-A\cdot D\tag{2} X(t+1)=w⋅X∗(t)−A⋅D(2) X ( t + 1 ) = w ⋅ X ∗ ( t ) + D p ′ ⋅ e b l ⋅ cos ( 2 π l ) (3) X(t+1)=w\cdot X^*(t)+D'_p\cdot e^{bl}\cdot\cos(2\pi l)\tag{3} X(t+1)=w⋅X∗(t)+Dp′⋅ebl⋅cos(2πl)(3)这样设计自适应调整权重 w w w的好处在于,其值由两部分决定,前半部分对种群迭代次数过大时起主要调节作用,后半部分对种群陷入局部最优时起主要调节作用。权重 w w w前后两部分会根据当前种群位置的变化情况而发生变化,不拘于某种固定的形式,具有很强的自适应性。
(2)自适应调整搜索策略
为防止算法陷入局部最优,随机搜索阶段,个体根据概率阈值 Q Q Q来选取随机搜索的更新方式,概率阈值定义为 Q = ∣ f ˉ − f min ∣ ∣ f max − f min ∣ (4) Q=\frac{|\bar f-f_{\min}|}{|f_{\max}-f_{\min}|}\tag{4} Q=∣fmax−fmin∣∣fˉ−fmin∣(4)其中, f ˉ \bar f fˉ表示当前鲸鱼种群的平均适应度值; f min f_{\min} fmin为当前鲸鱼种群中最好的适应度值; f max f_{\max} fmax为当前鲸鱼种群中最差的适应度值。对于每个鲸鱼个体,以一个 [ 0 , 1 ] [0,1] [0,1]之间的随机数 q q q与计算出的概率阈值 Q Q Q进行数值比较。若 q < Q qq<Q
,随机选取的鲸鱼个体 X rand X_{\text{rand}} Xrand根据式(5)更新其位置,其他鲸鱼个体位置不变;否则,其他鲸鱼个体根据基本公式更新其位置。这样设计使得算法在迭代前期能以较大的概率在全局范围内随机产生一组解,避免鲸鱼因聚集在一起而导致种群多样性的缺失,增强了算法的全局搜索能力。 X rand = X j min + r ⋅ ( X j max − X j min ) (5) X_{\text{rand}}=X_{j\min}+r\cdot(X_{j\max}-X_{j\min})\tag{5} Xrand=Xjmin+r⋅(Xjmax−Xjmin)(5)其中, r r r为 [ 0 , 1 ] [0,1] [0,1]之间的随机数; X j min X_{j\min} Xjmin和 X j max X_{j\max} Xjmax分别为变量 X rand X_{\text{rand}} Xrand取值的最小值和最大值。
(3)AWOA流程图
二、仿真对比与分析
本文测试函数以文献[1]中的f1~f3为例,以30维为例。经过反复多次仿真,对AWOA算法的最优参数设置如下:常数 b = 1 b=1 b=1, d 1 = 1 × 1 0 − 4 d_1=1×10^{-4} d1=1×10−4, d 2 = 1 × 1 0 − 4 d_2=1×10^{-4} d2=1×10−4,标准WOA[2]、CWOA[3]、IWOA[4]、CPWOA[5]和WOAWC[6]中的其他参数均按照其对应参考文献设置。种群规模 N = 30 N=30 N=30,最大迭代次数 M a x _ i t e r = 500 Max\_iter=500 Max_iter=500,每个算法独立运算30次。


函数:F1
WOA:最优值: 1.0275e-88,最差值:2.2887e-70,平均值:7.6347e-72,标准差:4.1784e-71
CWOA:最优值: 0,最差值:0,平均值:0,标准差:0
IWOA:最优值: 5.8869e-128,最差值:3.9601e-115,平均值:1.6159e-116,标准差:7.3161e-116
CPWOA:最优值: 7.5304e-40,最差值:2.4677e-31,平均值:1.5636e-32,标准差:5.1077e-32
WOAWC:最优值: 0,最差值:0,平均值:0,标准差:0
AWOA:最优值: 0,最差值:0,平均值:0,标准差:0
函数:F2
WOA:最优值: 197.2851,最差值:198.0525,平均值:197.7349,标准差:0.18177
CWOA:最优值: 197.236,最差值:197.8923,平均值:197.5488,标准差:0.15479
IWOA:最优值: 197.4065,最差值:198.1475,平均值:197.7051,标准差:0.17241
CPWOA:最优值: 0.27532,最差值:197.4893,平均值:55.9569,标准差:80.772
WOAWC:最优值: 197.0951,最差值:197.1861,平均值:197.1288,标准差:0.021044
AWOA:最优值: 197.0692,最差值:197.4661,平均值:197.2064,标准差:0.098759
AWOA:最优值: 196.9541,最差值:197.2277,平均值:197.1117,标准差:0.057015
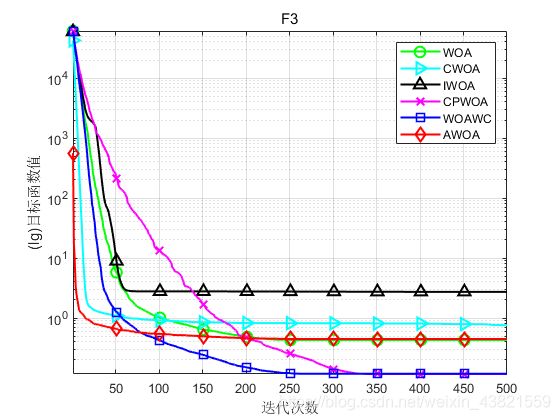
函数:F3
WOA:最优值: 0.080895,最差值:0.99112,平均值:0.43008,标准差:0.26211
CWOA:最优值: 0.33137,最差值:1.4031,平均值:0.75583,标准差:0.27682
IWOA:最优值: 0.72263,最差值:4.3749,平均值:2.7275,标准差:1.0025
CPWOA:最优值: 0.038945,最差值:0.21567,平均值:0.11654,标准差:0.0511
WOAWC:最优值: 0.045654,最差值:0.21824,平均值:0.11793,标准差:0.044555
AWOA:最优值: 0.14015,最差值:0.75181,平均值:0.44644,标准差:0.16601
仿真结果表明,AWOA在收敛精度和收敛速度方面总体上优于其他多种改进的鲸鱼优化算法。
三、参考文献
[1] 孔芝, 杨青峰, 赵杰, 等. 基于自适应调整权重和搜索策略的鲸鱼优化算法[J]. 东北大学学报(自然科学版), 2020, 41(1): 35-43.
[2] Seyedali M, Andrew L. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67.
[3] 王坚浩, 张亮, 史超, 等.基于混沌搜索策略的鲸鱼优化算法[J]. 控制与决策, 2019, 34(9): 1893-1900.
[4] 龙文, 蔡绍洪, 焦建军, 等. 求解大规模优化问题的改进鲸鱼优化算法[J]. 系统工程理论与实践, 2017, 37(11): 2983-2994.
[5] 黄清宝, 李俊兴, 宋春宁, 等.基于余弦控制因子和多项式变异的鲸鱼优化算法[J]. 控制与决策, 2020, 35(3): 559-568.
[6] 郭振洲, 王平, 马云峰, 等. 基于自适应权重和柯西变异的鲸鱼优化算法[J]. 微电子学与计算机, 2017, 34(9): 20-25.
