嵌入Circle映射和逐维小孔成像反向学习的鲸鱼优化算法
文章目录
- 一、理论基础
-
- 1、鲸鱼优化算法
- 2、改进鲸鱼优化算法
-
- (1)混沌序列初始化
- (2)逐维小孔成像反向学习
- (3)融合贝塔分布和逆不完全 Γ \Gamma Γ函数的权重
- (4)改进算法流程
- 二、仿真实验和结果分析
- 三、参考文献
一、理论基础
1、鲸鱼优化算法
请参考这里。
2、改进鲸鱼优化算法
(1)混沌序列初始化
本文采用Circle混沌映射来生成初始群体,Circle映射定义如下: x i + 1 = m o d ( x i + 0.2 − ( 0.5 2 π ) s i n ( 2 π x i ) , 1 ) (1) x_{i+1}=mod\left(x_i+0.2-\left(\frac{0.5}{2\pi}\right)sin(2\pi x_i),1\right)\tag{1} xi+1=mod(xi+0.2−(2π0.5)sin(2πxi),1)(1)利用Circle映射产生初始种群,相比于随机分布的种群,改进后的种群初始位置分布更加均匀,扩大了鲸鱼群在空间中的搜索范围,增加了群体位置的多样性,一定程度上改善了算法容易陷入局部极值的缺陷,从而提高了算法的寻优效率。
(2)逐维小孔成像反向学习
本文提出一种逐维小孔成像反向学习策略,通过结合小孔成像反向学习与逐维反向学习策略,对一个可行解逐维求反向解,使得算法获得摆脱局部极值的能力,公式如下: X b e s t ′ j = a j + b j 2 + a j + b j 2 n − X b e s t j n (2) X_{best}^{'j}=\frac{a_j+b_j}{2}+\frac{a_j+b_j}{2n}-\frac{X_{best}^j}{n}\tag{2} Xbest′j=2aj+bj+2naj+bj−nXbestj(2)其中, n n n为调节因子, a j a_j aj和 b j b_j bj分别是第 j j j维解的上下限。与一般反向学习相比,本文选择的是当前种群中保留的最优个体进行逐维反向学习,一定程度上降低了算法陷入局部最优的可能性,同时本文所提策略中 a j a_j aj和 b j b_j bj是动态变化的,相比于固定边界的反向学习策略具有更加准确的搜索范围,从而提高了算法的优化效率。
(3)融合贝塔分布和逆不完全 Γ \Gamma Γ函数的权重
本文提出一种融合贝塔分布和逆不完全 Γ \Gamma Γ函数的惯性因子调整方法,公式如下: w = w min + w max − w min λ × g a m m a i n c i n v ( λ , 1 − t T ) + σ B ( b 1 , b 2 ) (3) w=w_{\min}+\frac{w_{\max}-w_{\min}}{\lambda}×gammaincinv\left(\lambda,1-\frac tT\right)+\sigma B(b_1,b_2)\tag{3} w=wmin+λwmax−wmin×gammaincinv(λ,1−Tt)+σB(b1,b2)(3)其中, w max = 0.9 , w min = 0.4 w_{\max}=0.9,w_{\min}=0.4 wmax=0.9,wmin=0.4; g a m m a i n c i n v ( λ , a ) gammaincinv(\lambda,a) gammaincinv(λ,a)为逆不完全 Γ \Gamma Γ函数 γ ( λ , a ) = ∫ 0 λ e − t t a − 1 d t \gamma(\lambda,a)=\int_0^\lambda {e^{-t}t^{a-1}}\,{\rm d}t γ(λ,a)=∫0λe−tta−1dt的Matlab调用函数; λ ( λ ≥ 0 ) \lambda(\lambda≥0) λ(λ≥0)为随机变量,本文取 λ = 0.1 \lambda=0.1 λ=0.1; B ( b 1 , b 2 ) B(b_1,b_2) B(b1,b2)表示服从贝塔分布的随机数, b 1 = 1 , b 2 = 2 b_1=1,b_2=2 b1=1,b2=2; σ \sigma σ为惯性权重调整因子,本文取 σ = 0.1 \sigma= 0.1 σ=0.1,用来控制惯性权重 w w w的偏移程度,使其能够更好地平衡算法的全局搜索与局部开发能力; t t t为当前迭代次数; T T T为最大迭代次数,此时 a = 1 − t / T a=1-t/T a=1−t/T。
由式(3)可知,本文改进权重在总体上随着,迭代次数的增加而非线性递减,满足整个搜索过程权重的变化,同时,在该式中加入了服从贝塔分布的随机数,一方面在迭代前期,权值变化太快时也可能产生较大的权值,一定程度上增强了算法的全局搜索能力;另一方面到迭代后期,权重系数随着迭代次数增加而减小,而且变化比较平稳,此时加入服从贝塔分布的随机数可使算法有机会获得较大的权值,实现权重的动态变化,从而提高算法的收敛速度。结合WOA位置更新公式,MWOA公式定义如下: X ( t + 1 ) = w ⋅ X ∗ ( t ) − A ⋅ D , ∣ A ∣ < 1 , p < 0.5 ; (4) X(t+1)=w\cdot X^*(t)-A\cdot D,|A|<1,p<0.5;\tag{4} X(t+1)=w⋅X∗(t)−A⋅D,∣A∣<1,p<0.5;(4) X ( t + 1 ) = w ⋅ X rand − A ⋅ D rand , ∣ A ∣ ≥ 1 , p < 0.5 ; (5) X(t+1)=w\cdot X_{\text{rand}}-A\cdot D_{\text{rand}},|A|≥1,p<0.5;\tag{5} X(t+1)=w⋅Xrand−A⋅Drand,∣A∣≥1,p<0.5;(5) X ( t + 1 ) = D ′ ⋅ e b l ⋅ cos ( 2 π l ) + w ⋅ X ∗ ( t ) , p ≥ 0.5. (6) X(t+1)=D'\cdot e^{bl}\cdot\cos(2\pi l)+w\cdot X^*(t),p≥0.5.\tag{6} X(t+1)=D′⋅ebl⋅cos(2πl)+w⋅X∗(t),p≥0.5.(6)
本文通过结合混沌映射理论、逐维小孔成像反向学习策略、融合贝塔分布和逆不完全 Γ \Gamma Γ函数的权重来优化算法的寻优效率,提高算法的稳定性,以期望在每次迭代过程中获得更好的优化结果。
(4)改进算法流程
二、仿真实验和结果分析
为了验证本文所提出算法的鲁棒性,将改进鲸鱼优化算法(MWOA)与鲸鱼优化算法(WOA)、樽海鞘算法(SSA)和灰狼优化算法(GWO)同时在10个典型的基准测试函数(见表1)下进行30次对比实验,进而客观地反映算法改进的有效性。

注:f3更正为5维,f9更正为15维,f10更正为10维
本文实验最大迭代次数为1000,种群个数为30,各算法的主要参数设置参见文献[1]表2。结果显示如下:







函数:F1
WOA:最差值: 1.9129e-154,最优值:2.9979e-178,平均值:7.0819e-156,标准差:3.4959e-155
MWOA:最差值: 0,最优值:0,平均值:0,标准差:0
SSA:最差值: 1.1434e-09,最优值:1.9853e-10,平均值:6.805e-10,标准差:2.4082e-10
GWO:最差值: 3.7389e-114,最优值:3.0599e-122,平均值:1.3541e-115,标准差:6.8164e-115
函数:F2
WOA:最差值: 3.9488e-100,最优值:1.1588e-116,平均值:1.3844e-101,标准差:7.2057e-101
MWOA:最差值: 0,最优值:0,平均值:0,标准差:0
SSA:最差值: 10.4257,最优值:1.0748,平均值:4.1378,标准差:2.0493
GWO:最差值: 9.6193e-26,最优值:7.2198e-27,平均值:3.4649e-26,标准差:2.181e-26
函数:F3
WOA:最差值: 1.8087e-05,最优值:1.0443e-30,平均值:7.9126e-07,标准差:3.3221e-06
MWOA:最差值: 0,最优值:0,平均值:0,标准差:0
SSA:最差值: 2.1332e-10,最优值:8.931e-12,平均值:9.6075e-11,标准差:5.4816e-11
GWO:最差值: 2.2903e-104,最优值:4.3051e-122,平均值:1.2795e-105,标准差:4.5493e-105
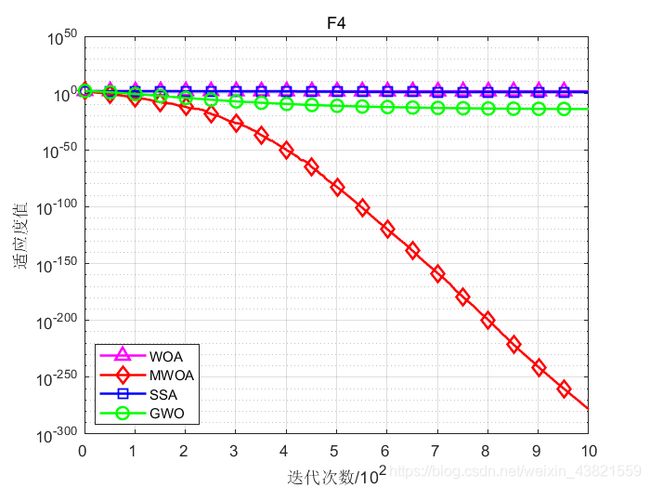
函数:F4
WOA:最差值: 90.7033,最优值:0.28381,平均值:44.8412,标准差:31.3353
MWOA:最差值: 2.6474e-277,最优值:1.6609e-296,平均值:8.8666e-279,标准差:0
SSA:最差值: 20.7784,最优值:2.2556,平均值:8.0388,标准差:3.9844
GWO:最差值: 6.4563e-14,最优值:4.3481e-16,平均值:1.0589e-14,标准差:1.3384e-14
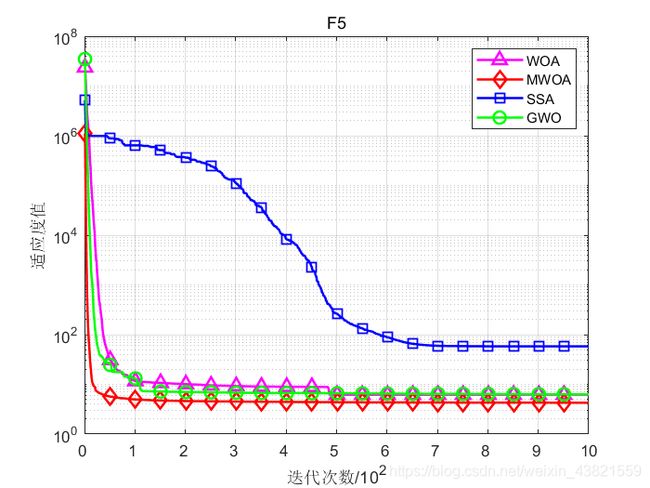
函数:F5
WOA:最差值: 8.9497,最优值:5.2924,平均值:6.1889,标准差:0.64226
MWOA:最差值: 5.0513,最优值:3.3525,平均值:4.2795,标准差:0.3755
SSA:最差值: 518.3665,最优值:2.6847,平均值:57.9862,标准差:115.1026
GWO:最差值: 8.3203,最优值:5.0299,平均值:6.2971,标准差:0.76275
函数:F6
WOA:最差值: 0.0046414,最优值:3.5583e-05,平均值:0.0010988,标准差:0.001339
MWOA:最差值: 2.9716e-05,最优值:6.0702e-07,平均值:5.858e-06,标准差:5.8873e-06
SSA:最差值: 0.18505,最优值:0.030908,平均值:0.094963,标准差:0.039095
GWO:最差值: 0.0023439,最优值:0.00020351,平均值:0.00089369,标准差:0.00050896
函数:F7
WOA:最差值: 7.9936e-15,最优值:8.8818e-16,平均值:4.204e-15,标准差:2.2726e-15
MWOA:最差值: 4.4409e-15,最优值:8.8818e-16,平均值:1.4803e-15,标准差:1.3467e-15
SSA:最差值: 3.9943,最优值:1.5392,平均值:2.5813,标准差:0.66258
GWO:最差值: 3.2863e-14,最优值:1.5099e-14,平均值:2.5876e-14,标准差:4.2226e-15
函数:F8
WOA:最差值: 0.13148,最优值:0,平均值:0.005183,标准差:0.024252
MWOA:最差值: 0,最优值:0,平均值:0,标准差:0
SSA:最差值: 0.053947,最优值:1.777e-08,平均值:0.017222,标准差:0.014971
GWO:最差值: 0.032642,最优值:0,平均值:0.0032469,标准差:0.0082083
函数:F9
WOA:最差值: 0.023846,最优值:7.6954e-05,平均值:0.003426,标准差:0.0062747
MWOA:最差值: 0.00013586,最优值:2.2293e-05,平均值:6.0564e-05,标准差:3.1324e-05
SSA:最差值: 5.5176,最优值:1.2497e-11,平均值:1.1462,标准差:1.3085
GWO:最差值: 0.026935,最优值:2.4386e-07,平均值:0.0047231,标准差:0.0087737
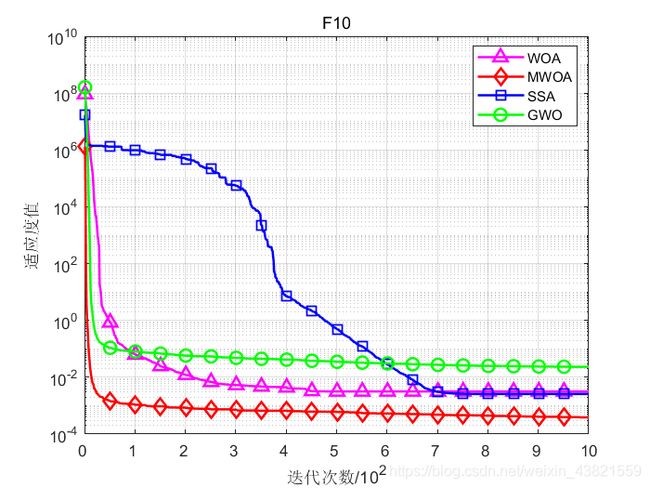
函数:F10
WOA:最差值: 0.012362,最优值:8.1303e-05,平均值:0.0031629,标准差:0.0046751
MWOA:最差值: 0.0011214,最优值:8.3654e-05,平均值:0.00038704,标准差:0.00023362
SSA:最差值: 0.010987,最优值:1.7949e-11,平均值:0.0025637,标准差:0.0047266
GWO:最差值: 0.20041,最优值:6.4174e-07,平均值:0.023303,标准差:0.050379
实验结果表明,改进算法在求解效率和稳定性等方面都有较大提升,同时,算法的寻优精度和收敛速度也比原始算法更优秀。
三、参考文献
[1] 张达敏, 徐航, 王依柔, 等. 嵌入Circle映射和逐维小孔成像反向学习的鲸鱼优化算法[J]. 控制与决策, 2021, 36(5): 1173-1180.
