爆火的的Transformer,到底火在哪?
传送门:
第一章 细讲:Attention模型的机制原理
第二章 Attention实现超详细解析( tfa, keras 方法调用源码分析 & 自建网络)
推荐阅读:The Illustrated Transformer——Jay Alammar
目录
- 前言
- 1.总体架构
- 2.基本单元
-
- 2.1 Word Embedding (词嵌入)
- 2.2 Self- Attention
- 2.3 Multi-Head Attention (MHA)
- 2.4 Positional Encoding (位置编码)
- 2.5 The Residuals (残差连接) & Layer Normalization(层归一化)
- 2.6 Feed Forward Network (前馈全连接模块)
- 2.7 Softmax Layer
- 3. 编码器-解码器结构
-
- 3.1 Encoder
- 3.2 Decoder
- 3.3 Encoder-Decoder Attention
- 3.4 Encoder和Decoder有哪些不同?
- 4. 补充
-
- 4.1 Transformer的特点
- 4.2 Transformer VS RNN
- 4.3 Transformer存在的问题
- 4.4 基于Transformer的预训练语言生成模型
- 总结
- 参考
前言
与传统的 Soft Attention(如Bahdanau Attention、Luong Attention) 相比, Self-Attention 可有效缩短远距离依赖特征之间的距离,更容易捕获时间序列数据中相互依赖的特征,在大多数实际问题中,Self-Attention 更被研究者们所青睐,并具有更加优异的实际表现。
Transformer在Goole的一篇论文Attention is all you need被提出,其火爆程度相信已经不需要我多说了,大部分AIers应该都听过Transformer。本人在接下来的课题研究中也会用到与之有关的知识,因此,结合网上一些已有的博客(尤其感谢Alammar教授[1])以及Attention is all you need这篇paper,本篇文章对Transformer做一个详细的个人理解记录。
Transformer是我的一个重点学习、讲解内容,如果有哪里写的不对,欢迎大家批评指正,感谢~
1.总体架构
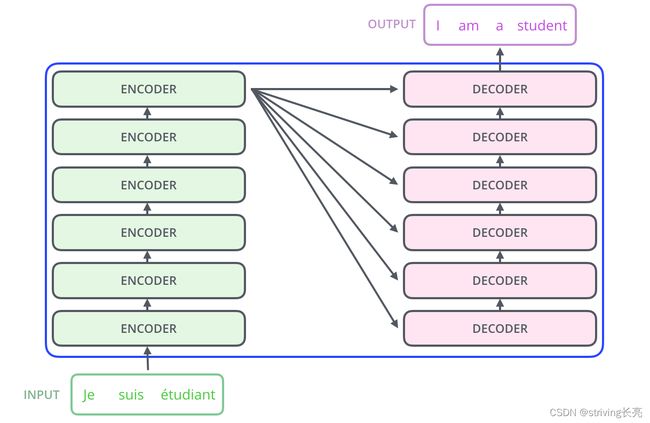
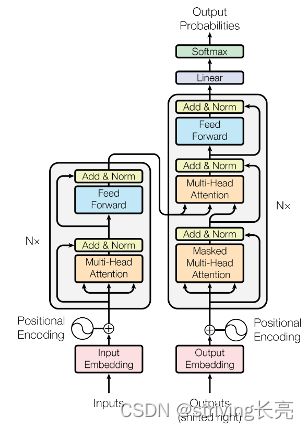
以机器翻译为例,先整体看一下Tranformer的结构,注意:Encoders和Decoders均为N层:
如果我们把Transformer想象成一个黑匣子,在机器翻译的领域中,这个黑匣子的功能就是输入一种语言然后将它翻译成其他语言。如下图所示:

这个黑匣子主要有两部分构成,分别是Encoders以及Decoders:
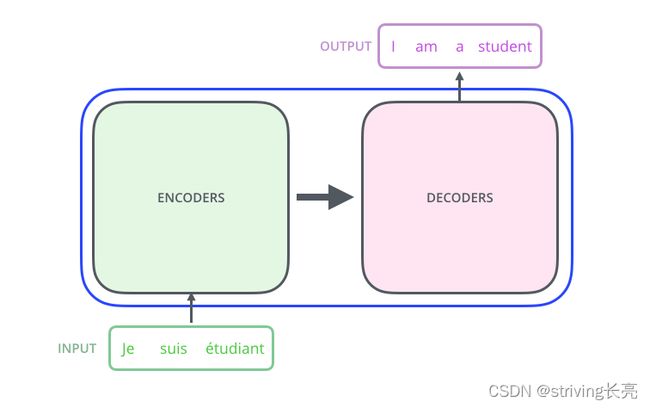
具体地说,每一个Encoder和Decoder分别由6个子Encoder以及Decoder构成(论文中是这么配置的),有一个细节,最顶端Encoder的输出会传递给每一个Decoders:
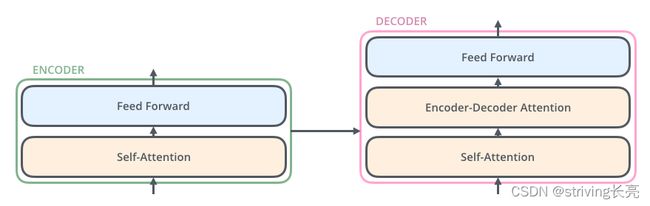
对于Encoders中的每一个Encoder,结构都是相同的,但并不会共享权值。每层Encoder有2个部分组成,如下图:

每个Encoder的输入首先会通过一个self-attention层,通过self-attention层帮助Endcoder在编码单词的过程中查看输入序列中的其他单词。
Self-attention的输出会被传入一个全连接的前馈神经网络,每个encoder的前馈神经网络参数个数都是相同的,但他们的作用是独立的。
每个Decoder也同样具有这样的层级结构,但是在这之间有一个Attention层,帮助Decoder专注于与输入句子中对应的那个单词(类似与seq2seq models的结构)
2.基本单元
2.1 Word Embedding (词嵌入)
首先,我们需要将单词变成词向量形式,不明白的可以看Glossary of Deep Learning: Word Embedding,我也会在接下来的新文章中详细介绍一下Word Embedding。
每个单词都嵌入到大小为512的向量中。我们将用这些简单的方框来表示这些向量。

词嵌入的过程只发生在最底层的Encoder。并且Encoder的输入输出维度不会发生变化:
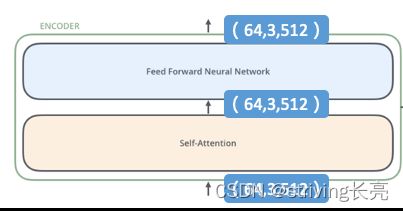
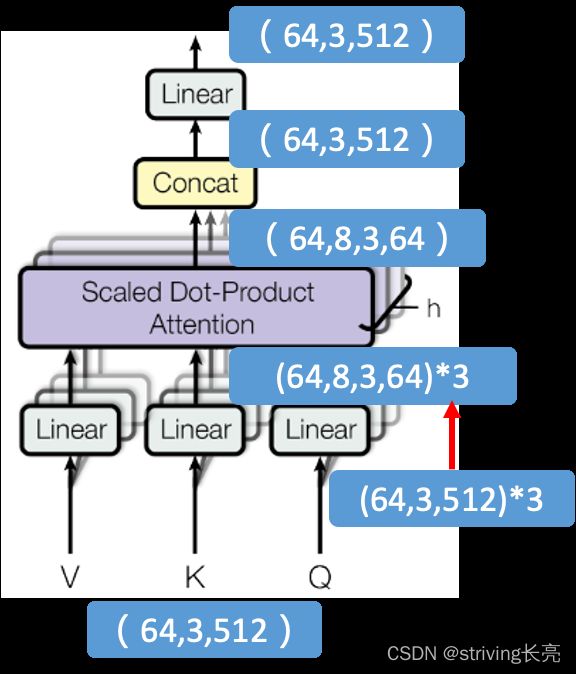
64是batch_size,3是单词个数,512是词向量维度。Transformer中的每个Encoder接收一个512维度的向量的列表作为输入,然后将这些向量传递到self-attention层,self-attention层产生一个等量512维向量列表,然后进入前馈神经网络,前馈神经网络的输出也为一个512维度的列表,然后将输出向上传递到下一个encoder。
因此,对于所有的Encoder来说,我们都可以按下图来理解,具体地:
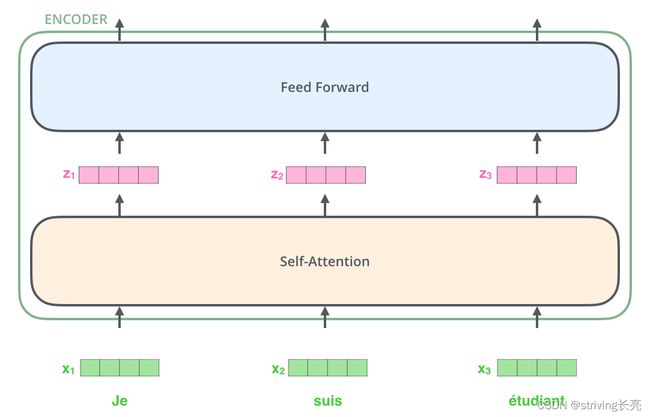
输入(一个向量的列表,每个向量的维度为512维,在最底层Encoder作用是词嵌入,其他层就是其前一层的output)。
另外这个列表的大小和词向量维度的大小都是可以设置的超参数。一般情况下,它是我们训练数据集中最长的句子的长度。
注意观察,在每个单词进入Self-Attention层后都会有一个对应的输出。Self-Attention层中的输入和输出是存在依赖关系的,而前馈层则没有依赖,每个单词对应一个独立的前馈神经网络层(网络层结构相同),所以在前馈层,我们可以用到并行化来提升速率。
2.2 Self- Attention
Self- Attention是Transformer的重点,与 Soft Attention 所不同的是,Self-Attention 是 Encoder 内部或者 Decoder 内部之间所发生的注意力机制,是由 Google AI 研究院所提出的预训练语言表征模型——BERT(Bidirectional Encoder Representations from Transformers) 的主要组成部分之一。
由于包括 LSTM、GRU 在内的众多 RNN 模型需按照固定方向顺序计算,为有效缩短远距离依赖特征之间的距离,在 Self-Attention 中,各隐藏层状态可通过特定的计算步骤被直接联系,也就是说,各隐藏层状态不必按照固定方向顺序串联
因此,Self-Attention 更容易捕获时间序列数据中相互依赖的特征。
关于注意力机制的部分在已经在我之前的文章做了详细的阐述,在此不再赘述,只是大体再做一个总结。
传送门:细讲:Attention模型的机制原理

Self- Attention的计算涉及三个对象:
-
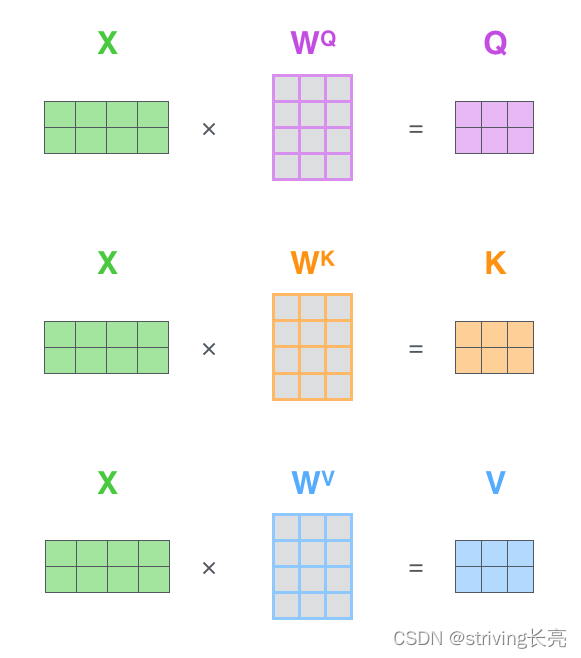
查询序列 Q:在 Self-Attention 中,Q 用于检索序列之间的信息。Q 由查询序列隐向量所组成,即 Q = X ∗ W Q Q=X*W^{Q} Q=X∗WQ, Q = [ q 1 ; q 2 ; … ; q n ] ∈ R d ∗ n Q= [q_{1}; q_{2};…; q_{n} ] ∈ ℝ ^{d∗ n} Q=[q1;q2;…;qn]∈Rd∗n ,由 n n n 个维度为 d d d的 列向量组成,其中 q i q_{i} qi 代表第 i i i 个列向量,表示该序列第 i i i个位置的隐状态。
-
键序列K,:作为被检索的序列,键序列是查询序列的匹配对象。 K = X ∗ W K K=X*W^{K} K=X∗WK, K = [ k 1 ; k 2 ; … ; k n ] ∈ R d ∗ n K= [k_{1} ; k_{2} ;…;k_{n} ] ∈ ℝ ^{d∗ n} K=[k1;k2;…;kn]∈Rd∗n ,也是由 n n n 个维度为 d d d的 列向量组成,其中 k i k_{i} ki代表键序列和值序列中第 i i i 个位置的隐向量。
-
值序列V:模型计算Query和各个Key的相似性或者相关性,再利用softmax函数,得到每个Key对应Value的权重系数,然后对Value进行加权求和,即得到了最终的Attention值。
本质上Attention机制是对Source中元素的Value值进行加权求和,而Query和Key用来计算对应Value的权重系数。 V = X ∗ W V V=X*W^{V} V=X∗WV,由键序列 V = [ v 1 ; v 2 ; … ; v m ] ∈ R d ∗ m V= [v_{1} ; v_{2} ;…;v_{m} ] ∈ ℝ ^{d∗ m} V=[v1;v2;…;vm]∈Rd∗m ,由 m m m个维度为 d d d 的列向量组成, v i v_{i} vi 代表值序列中第 i i i 个位置的隐向量。
X矩阵中的每一行对应于输入句子中的一个单词。我们再次看到词嵌入向量(512,或图中的4个框)和q/k/v向量(64,或图中的3个框)的大小差异:
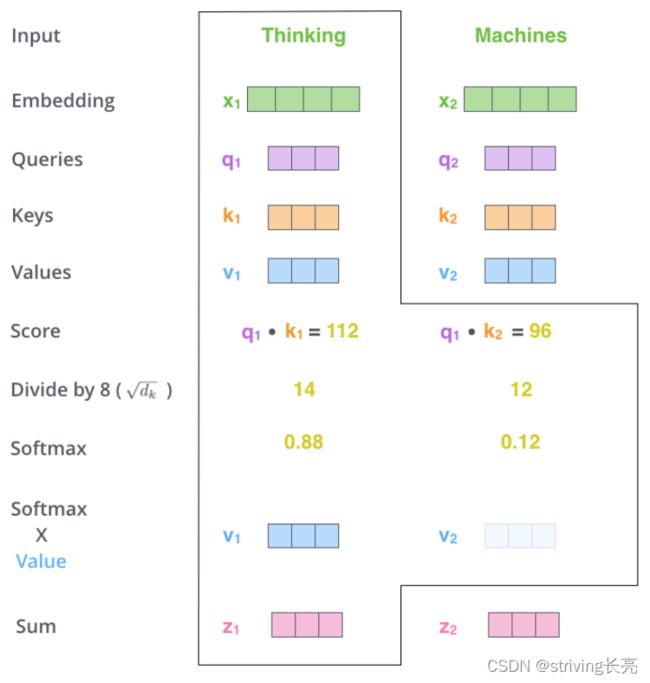
Attention ( Q , K , V ) = softmax ( Q K T d k ) V \operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V Attention(Q,K,V)=softmax(dkQKT)V
其中, Attention ( Q , K , V ) \operatorname{Attention}(Q, K, V) Attention(Q,K,V) 为一个维度为 d ∗ m d*m d∗m 的矩阵。在具体实现中,随着隐向量维度 d d d增大,点乘的方差也在逐渐增大,在计算Softmax的时候会出现梯度消失的情况,因为计算过程加了 d k \sqrt{d_{k}} dk 归一化因子,归 一化因子可有效缓解梯度消失情况的发生,并保证点乘结果的方差不随隐藏层维度 d 变化。
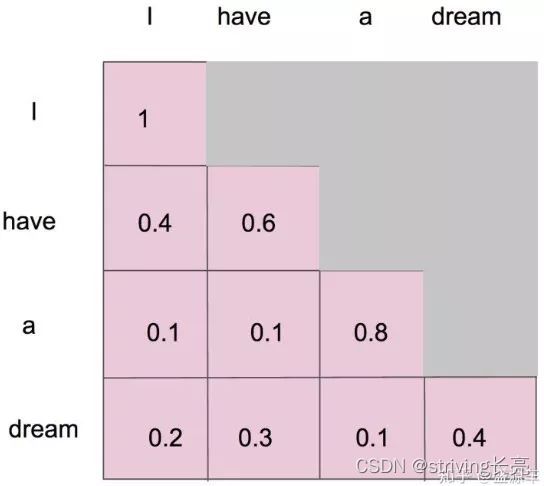
注意看这个公式, Q K T Q K^{T} QKT其实就会组成一个word2word的attention map!(加了softmax之后就是一个合为1的权重了)。比如说你的输入是一句话 “i have a dream” 总共4个单词,这里就会形成一张4x4的注意力机制的图:

这样一来,每一个单词就对应每一个单词有一个权重。
注意encoder里面是叫self-attention,decoder里面是叫masked self-attention。
这里的masked就是要在做language modelling(或者像翻译)的时候,不给模型看到未来的信息,即采用教师强制(Teacher- forcing)模式进行训练。
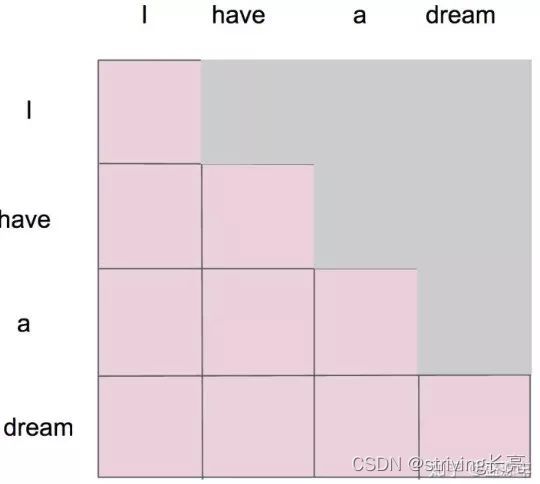
mask就是沿着对角线把灰色的区域用0覆盖掉,不给模型看到未来的信息。详细来说,i作为第一个单词,只能有和i自己的attention。have作为第二个单词,有和i, have 两个attention。 a 作为第三个单词,有和i,have,a 前面三个单词的attention。到了最后一个单词dream的时候,才有对整个句子4个单词的attention。
需要说明的是,键序列和值序列一般是具有对应关系的,即 m = n m=n m=n,也就是三者的维度一致,但在实际计算当中,并不强制要求三者维度一致,即便值序列的维度与键序列不一致,也不会导致错误发生。
2.3 Multi-Head Attention (MHA)
Multi-headed的机制是Transformer的另外一个特色,其目的是进一步完善self-attention层。
原始的attention, 就是一个query 和一组key算相似度, 然后对一组value做加权和; 假如每个Q和K都是512维的向量, 那么这就相当于在512维的空间里比较了两个向量的相似度.
multi-head相当于把这个512维的空间人为地拆成了多个子空间, 比如head number=8, 就是把一个高维空间分成了8个子空间, 相应地,V也要分成8个head; 然后在这8个子空间里分别计算Q和K的相似度, 再分别组合V. 这样可以让attention能从多个不同的角度进行结合, 这对于NMT是很有帮助的, 因为我们在翻译的时候源语言和目标语言的词之间并不是一一对应的, 而是受很多词共同影响的. 每个子空间都会从自己在意的角度或者因素去组合源语言, 从而得到最终的翻译结果.
以”The animal didn’t cross the street because it was too tired”这句话为例。这句话中的"it"指的是什么?它指的是“animal”还是“street”?
Multi-headed主要有以下作用:
-
拓展了模型关注不同位置的能力。在上面例子中可以看出,上图是我们第五层Encoder针对单词’it’的图示,可以发现,我们的Encoder在编码单词‘it’时,部分注意力机制集中在了‘animal’上,这部分的注意力会通过权值传递的方式影响到’it’的编码,这在对语言的理解过程中是很有用的。 -
为attention层提供了多个representation subspaces。由下图可以看到,在self-attention中,我们有多个个Query / Key / Value权重矩阵(Transformer使用8个attention heads)。这些集合中的每个矩阵都是随机初始化生成的。然后通过训练,用于将词嵌入(或来自较低Encoder/Decoder的矢量)投影到不同的representation subspaces(表示子空间)中。
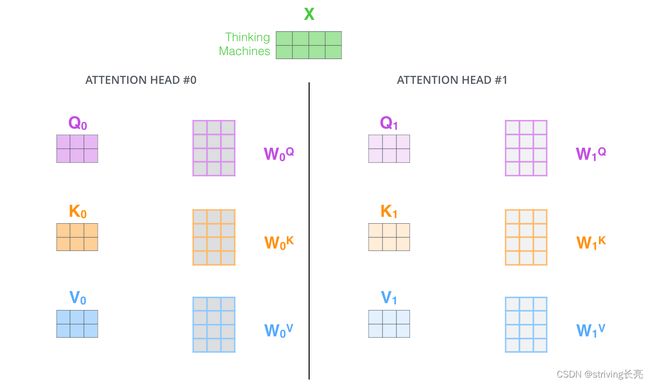
通过multi-headed attention,我们为每个“header”都独立维护一套Q/K/V的权值矩阵。然后我们还是如之前单词级别的计算过程一样处理这些数据。
因为我们有8头attention,所以我们会在八个时间点去计算这些不同的权值矩阵,但最后结束时,我们会得到8个不同的矩阵。
由于self-attention后面紧跟着的是前馈神经网络,而前馈神经网络接受的是单个矩阵向量,而不是8个矩阵。所以我们把这8个矩阵压缩成一个矩阵,将这8个矩阵连接在一起然后再与另一个权重矩阵 W O W^{O} WO相乘。
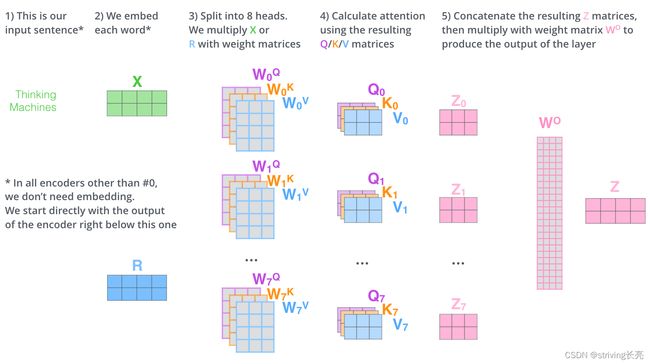
MultiHead ( Q , K , V ) = Concat ( head 1 , … , head h ) W O where head = Attention ( Q W i Q , K W i K , V W i V ) \begin{aligned} \operatorname{MultiHead}(Q, K, V) &=\text { Concat }\left(\text { head }_{1}, \ldots, \text { head }_{\mathrm{h}}\right) W^{O} \\ \text { where head } &=\text { Attention }\left(Q W_{i}^{Q}, K W_{i}^{K}, V W_{i}^{V}\right) \end{aligned} MultiHead(Q,K,V) where head = Concat ( head 1,…, head h)WO= Attention (QWiQ,KWiK,VWiV)
W i Q ∈ R d model × d k , W i K ∈ R d mode × d k , W i V ∈ R d model × d v W_{i}^{Q} \in \mathbb{R}^{d_{\text {model }} \times d_{k}}, W_{i}^{K} \in \mathbb{R}^{d_{\text {mode }} \times d_{k}}, W_{i}^{V} \in \mathbb{R}^{d_{\text {model }} \times d_{v}} WiQ∈Rdmodel ×dk,WiK∈Rdmode ×dk,WiV∈Rdmodel ×dv,对于其中的每一个,我们使用 d k = d v = d m o d e l / h = 64 d_{k} = d_{v} = d_{model}/h = 64 dk=dv=dmodel/h=64。由于每个头的维度减少,总计算成本类似于具有全维度的单头注意力。
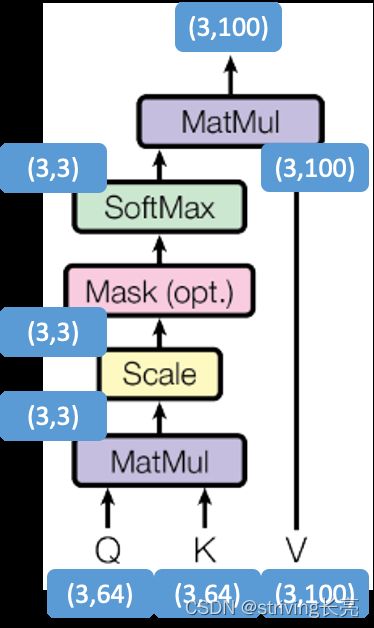
总体计算过程维度变化如图所示:
2.4 Positional Encoding (位置编码)
模型不包括Recurrence/Convolution,因此是无法捕捉到序列顺序信息的,例如将K、V按行进行打乱,那么Attention之后的结果是一样的。但是序列信息非常重要,代表着全局的结构,因此必须将序列的分词相对或者绝对position信息利用起来。
回想一下attention,任意一对(query, key)的计算都是完全一样的,不像CNN和RNN,有一个位置或者时序的差异:
- CNN框住一块区域,随着卷积核移动,边缘的少量点会跟着有序变化;
- RNN更明显,不同时序的 h t h_{t} ht 和 s t s_{t} st不同,而且是随着输入顺序不同(正序,倒序)而不同。
因此为了体现出时序或者在序列中的位置差异,要对input加入一定的位置信息,即positional embedding。
为了解决输入序列中的单词顺序问题,transformer为每个输入单词的词嵌入上添加了一个新向量-位置向量。这些位置编码向量有固定的生成方式,所以获取他们是很方便的,但是这些信息确是很有用的,他们能捕捉到每个单词的位置,或者序列中不同单词之间的距离。将这些信息也添加到词嵌入中,然后与Q/K/V向量点击,获得的attention就有了距离的信息了。
编码器和解码器的底部输入,位置编码与词嵌入具有相同的维度 d m o d e l d_{model} dmodel,因此可以将两者相加。位置编码有很多选择,主要包括可学习的和固定的基于正余弦的位置编码。
P E ( p o s , 2 i ) = sin ( p o s / 1000 0 2 i / d model ) P E ( p o s , 2 i + 1 ) = cos ( p o s / 1000 0 2 i / d mold ) \begin{aligned} P E_{(p o s, 2 i)} &=\sin \left(p o s / 10000^{2 i / d_{\text {model }}}\right) \\ P E_{(p o s, 2 i+1)} &=\cos \left(p o s / 10000^{2 i / d_{\text {mold }}}\right) \end{aligned} PE(pos,2i)PE(pos,2i+1)=sin(pos/100002i/dmodel )=cos(pos/100002i/dmold )
其中, pos 是位置,也就是文本序列位置的索引,i 是维度索引。也就是说,位置编码的每个维度对应一个正弦曲线。波长形成从 2π 到 10000 · 2π 的几何级数。我们选择这个函数是因为我们假设它可以让模型轻松学习通过相对位置来参与,因为对于任何固定的偏移量 k, P E p o s + k PE_{pos+k} PEpos+k 可以表示为 P E p o s PE_{pos} PEpos 的线性函数。
Position Embedding本身是一个绝对位置的信息,但在语言中,相对位置也很重要,Google选择前述的位置向量公式的一个重要原因是,由于我们有:
sin ( α + β ) = sin α cos β + cos α sin β cos ( α + β ) = cos α cos β − sin α sin β \begin{aligned} &\sin (\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta \\ &\cos (\alpha+\beta)=\cos \alpha \cos \beta-\sin \alpha \sin \beta \end{aligned} sin(α+β)=sinαcosβ+cosαsinβcos(α+β)=cosαcosβ−sinαsinβ
这表明位置p+k的向量可以表示成位置p的向量的线性变换,这提供了表达相对位置信息的可能性。
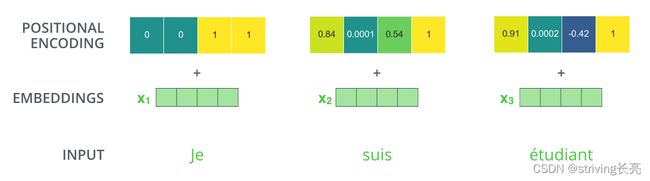
每一行都代表着对一个矢量的位置编码。因此第一行就是我们输入序列中第一个字的嵌入向量,每行都包含512个值,每个值介于1和-1之间,左半部分的值是一由一个正弦函数生成的,而右半部分是由另一个函数(余弦)生成。然后将它们连接起来形成每个位置编码矢量。
Transformer还尝试了使用可学习的位置嵌入,但发现这两个版本产生了几乎相同的结果。因此选择了正弦版本,因为它可以让模型推断出比训练期间遇到的序列长度更长的序列长度。
2.5 The Residuals (残差连接) & Layer Normalization(层归一化)
经过了前面的叙述,进一步探究了其内部的计算方式,上图可以转化为下图。
Add代表了Residual Connection,是为了解决多层神经网络训练困难的问题,通过将前一层的信息无差的传递到下一层,可以有效的仅关注差异部分,这一方法之前在图像处理结构如ResNet等中常常用到。
Norm则代表了Layer Normalization,通过对层的激活值的归一化,可以加速模型的训练过程,使其更快的收敛。
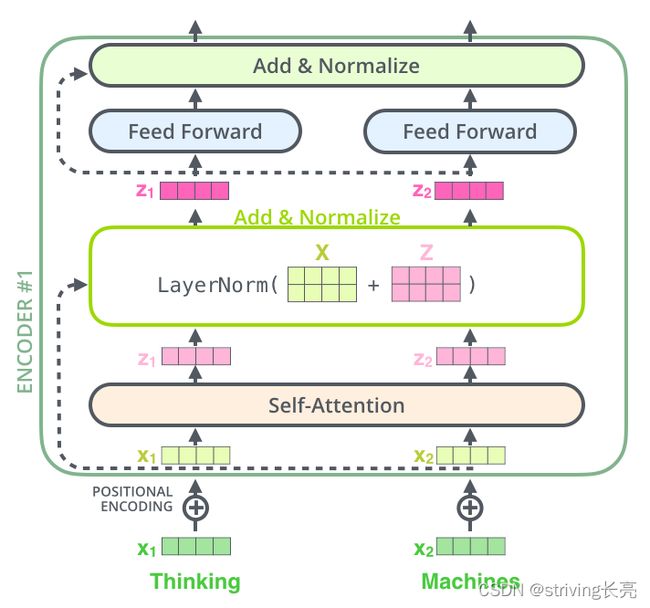
在每个sub-layer我们都模拟了残差网络,每个sub-layer的输出都是:
LayerNorm ( x + Sublayer ( x ) ) \text { LayerNorm }(x+ \text { Sublayer }(x)) LayerNorm (x+ Sublayer (x))
其中,Sublayer(x) 表示Sub-layer对输入 x 做的映射,为了确保连接,所有的sub-layers和embedding layer输出的维数都相同
-
残差连接一般附在另一个模块之上,其作用是将该模块的输入 x x x以及该模块的输出 f ( x ) f(x) f(x)相加作为最终的输出结果 x + f ( x ) x+f(x) x+f(x),当输入为向量或者矩阵时,该相加操作为向量或者矩阵对应位置的逐元素的相加。
在模型层数比较多的情况下,残差连接方式可将模型底层的信息在衰减较少的情况下传递到模型的高层。比如:输入端存在位置编码,残差连接使得位置信息不会随着多次编码而逐渐消失,同时,在深层网络的反向传播中,误差信号可经过残差连接构建恒等映射,从而直接从模块的输出端传播到模块的输入端,在一定程度上也可缓解梯度消失的问题。 -
层归一化可对输入的向量进行归一化操作,可使特征的方差在不同深度的模块中保持一定地范围,在训练Transformer等深层模型中,可使梯度更加稳定。
2.6 Feed Forward Network (前馈全连接模块)
除了注意力子层之外,Transformer的编码器和解码器中的每一层都包含一个完全连接的前馈网络(每一个输入独立),该网络分别且相同地应用于每个位置,包括两个线性变换,中间有一个 ReLU 激活:
FFN ( x ) = max ( 0 , x W 1 + b 1 ) W 2 + b 2 \operatorname{FFN}(x)=\max \left(0, x W_{1}+b_{1}\right) W_{2}+b_{2} \\ FFN(x)=max(0,xW1+b1)W2+b2
在论文的介绍中,输入以及输出维数 D m o d e l = 512 D_{model}=512 Dmodel=512,内层维数DFF=2048,如图所示:

2.7 Softmax Layer
假设实验中我们的模型从训练数据集上总共学习到1万个英语单词(“Output Vocabulary”)。这对应的Logits矢量也有1万个长度-每一段表示了一个唯一单词的得分。在线性层之后是一个softmax层,softmax将这些分数转换为概率。选取概率最高的索引,然后通过这个索引找到对应的单词作为输出。
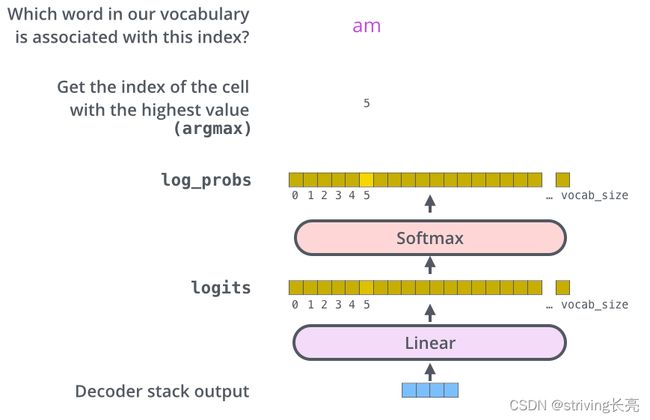
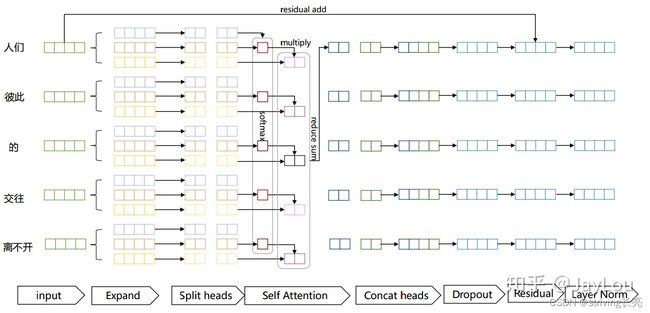
具体执行过程如图所示:
- Expand: 实际上是经过线性变换,生成Q、K、V三个向量
- Split heads: 分头操作,在原文中是将原来每个位置的512维分成8个head,每个head维度为512/8=64
- Self- Attention: 对每个head进行注意力计算
- Concat heads: 对进行完的Attention计算的每个head进行拼接
3. 编码器-解码器结构
经过上面的基本单元叙述,Transformer的编码器-解码器结构如下图所示 (如:Encoder和Decoder均为2层):
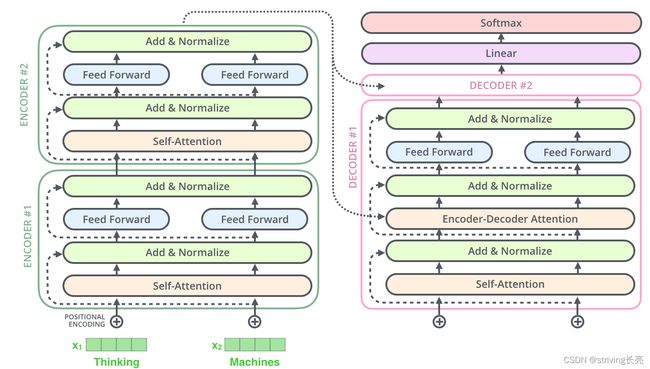
3.1 Encoder
每层Encoder包括两个sub-layers:
-
第一个sub-layer是multi-head self-attention mechanism,用来计算输入的self-attention
-
第二个sub-layer是简单的全连接网络。
Encoder部分在前文已经做了很详细的叙述,在此不再赘述。
3.2 Decoder
每层Decoder包括3个sub-layers:
-
第一个是Masked multi-head self-attention,也是计算输入的self-attention,但是因为是生成过程,因此在时刻 i 的时候,大于 i 的时刻都没有结果,只有小于 i 的时刻有结果,因此需要做Mask。 在Decoder中,self attention只关注输出序列中的较早的位置。这是在self attention计算中的softmax步骤之前屏蔽了特征位置(设置为 -inf)来完成的。
-
第二个sub-layer是对encoder的输入进行attention计算,也就是
Encoder-Decoder Attention。 -
第三个sub-layer是全连接网络,与Encoder相同
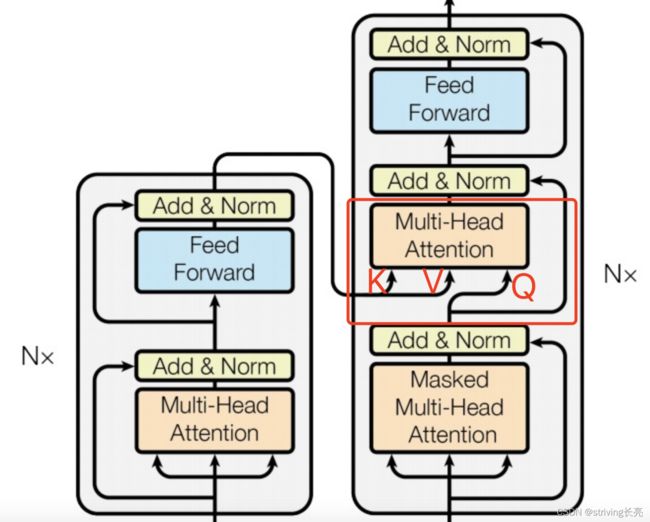
3.3 Encoder-Decoder Attention
重点讲一下Encoder-Decoder Attention,Encoder-Decoder Attention在Decoder层发生,并在MHA之后的一层,FFN之前。
“Encoder-Decoder Attention”层的工作方式与"Multi-Headed Self-Attention"一样
所不同的是,Encoder-Decoder Attention的查询矩阵,即Query来自于Decoder当前多头掩码注意力的输出,也就是说,它从下面的层创建其Query矩阵,并在Encoder堆栈的输出中获取Key和Value的矩阵,即键值矩阵均来自Transformer中Encoder的输出。
Encoder-Decoder Attention使得Decoder中的每一个位置都能参与输入序列中的所有位置。 这模仿了序列到序列模型中典型的编码器-解码器注意力机制。
Encoder-Decoder Attention通过计算输出序列对输入序列的注意力来更新解码器的隐状态矩阵。
3.4 Encoder和Decoder有哪些不同?
- MHA有所不同,Decoder中的self attention与Encoder的self attention略有不同:
Encoder中不需要Masked,Decoder中的self-attention层需要进行修改,因为只能获取到当前时刻之前的输入,因此只对时刻 t 之前的时刻输入进行attention计算,这也称为Mask操作。这里的masked就是要在做language modelling(或者像翻译)的时候,不给模型看到未来的信息,即采用教师强制(Teacher- forcing)模式进行训练,以保证其自回归分解形式。需要注意的是,在测试时,模型采用自由运行 (Free-run)模式进行生成。 - Decoder的最后输出部分还有一个Linear层以及Softmax层
- Decoder存在一个“Encoder-Decoder Attention”,在MHA之后,FFN之前。
综上,Transformer的执行过程如图所示:
紧接着,执行接下来的操作:
4. 补充
4.1 Transformer的特点
- Transformer解码器中的多头掩码注意力机制使在训练时计算当前位置的隐状态不会利用该位置后方的“未来”信息,保证了训练和测试阶段的一致性,保证了自回归分解形式(preserve the auto-regressive property)。
- 多头注意力允许模型在不同的位置共同关注来自不同表示子空间的信息,提升了模型关注到序列不同位置的能力。
- 由于Transformer模型中没有递归和卷积的部分,为了使模型能够学习到序列的顺序信息,我们必须注入一些相对或者绝对的位置信息。于是引入了位置编码。
4.2 Transformer VS RNN
-
并行计算, 提高训练速度
Transformer用attention代替了原本的RNN; 而RNN在训练的时候, 当前step的计算要依赖于上一个step的hidden state的, 也就是说这是一个sequential procedure, 我每次计算都要等之前的计算完成才能展开. 而Transformer不用RNN,所有的计算都可以并行进行, 从而提高的训练的速度. -
self-attention的计算复杂度低
在输入序列长度适中(不大于隐状态维度),相比卷积层、Rnn层,Self-Attention的计算复杂度都要低,更有优势。假设隐向量维度为d,序列长度为d,SA的计算复杂度为 O ( n 2 ⋅ d ) O(n^{2} \sdot d) O(n2⋅d),RNN为 O ( n ⋅ d 2 ) O(n \sdot d^{2}) O(n⋅d2),在 d > > n d>>n d>>n时,SA的计算复杂度远低于RNN的计算复杂度 -
建立直接的长距离依赖
self-attention 的远程依赖关系的学习能力比较强。在许多序列转化任务中,远距离依赖关系的学习是一个关键的挑战。原本的RNN里, 如果第一帧要和第十帧建立依赖, 那么第一帧的数据要依次经过第二三四五…九帧传给第十帧, 进而产生二者的计算. 而在这个传递的过程中, 可能第一帧的数据已经产生了biased, 因此这个交互的速度和准确性都没有保障. 而在Transformer中, 由于有self attention的存在, 任意两帧之间都有直接的交互, 从而建立了直接的依赖, 无论二者距离多远。Transformer中输入序列的任意两个位置之间的路径长度为 O ( 1 ) O(1) O(1),RNN中首尾之间的路径长度为 O ( n ) O(n) O(n),也就是与序列长度成正比。 -
RNN本质上是序列模型,而Transformer本质上为连接图模型
Transformer在序列依赖建模上更灵活,表达能力更强。在用于编码的Transformer结构中,每个位置与气其他所有位置(包括自身)都有注意力连接边,在用于解码的结构中,当前位置可看到所有前面的位置,因此,这是一种全连接的图模型,RNN则是典型的序列模型,当前位置只能看到序列规定方向的前缀信息。 -
Transformer训练稳定性低于RNN
RNN在训练时采用各种基于梯度下降的优化器即可优化,收敛速度快且训练稳定。而Transformer在优化时需使用一些训练技巧以提升训练稳定性,如Warmup技巧(实验显示,Transformer在直接使用传统梯度下降方法时性能会收到较为严重的影响)。Transformer的梯度会随着层数的变深而快速增大,这可能会导致Transformer训练初期的不稳定。
4.3 Transformer存在的问题
- 长距离依赖问题
虽然Transformer模型比RNN模型能更有效地建模序列中地长距离依赖关系,但是其最大能建模的序列长度也受到了空间复杂度的限制,具体来说,就是模型所使用的空间与文本长度的平方成正比,因此输入的文本长度不能超过一个上限值。当该长度超过上限时,文本会被截断,长距离依赖信息也会因此丢失。
改进:Transformer-XL - 运算复杂度问题
由于Transformer模型采用全连接的自注意力机制,其空间复杂度和时间复杂度均与输入文本长度的平方成正比,所以在长文本的建模中有较高的计算开销。
改进:Sparse Transformer、StarTransformer
4.4 基于Transformer的预训练语言生成模型
Transformer的提出极大地促进了大规模预训练语言生成模型的发展,主要模型如下:
- Generative Pre-Training (GPT)
- BERT(Bidirectional Encoder Representations from Transformers)
…
BERT 中的Transformer 使用双向self-attention,而GPT 中的Transformer 使用受限制的self-attention,其中每个token只能处理其左侧的上下文。
什么是单向Transformer?在Transformer的文章中,提到了Encoder与Decoder使用的Transformer Block是不同的。在Decoder Block中,使用了Masked Self-Attention,即句子中的每个词,都只能对包括自己在内的前面所有词进行Attention,这就是单向Transformer。
双向 Transformer 通常被称为“Transformer encoder”,而左侧上下文被称为“Transformer decoder”,decoder是不能获要预测的信息的

-
GPT模型在大规模文本语料上进行预训练,采用单向语言模型相同的训练目标进行参数优化,其实就是直接应用Transformer Decoder,GPT使用的Transformer结构就是将Encoder中的Self-Attention替换成了Masked Self-Attention
-
Bert中训练的是双向语言模型,应用了Transformer Encoder部分,不过在Encoder基础上还加了Masked Language Model (MLM)以及Next Sentence Prediction (NSP)
总结
完全不依赖于RNN结构仅利用Attention机制的Transformer由于其并行性和对全局信息的有效处理使其获得了较之前方法更好的翻译结果,在这基础上,Attention和Transformer架构逐步被应用在自然语言处理及图像处理等领域,
可以说,Transformer在各领域均取得了显著的成绩,是如今的一个热门使用模型,很多研究者也基于传统的Transformer提出了很多改进版本,Transformer的提出大大促进了包括自然语言处理在内的众多领域的发展,对于Transformer模型结构的应用以及改进也是如今的一个热点研究方向,值得众多研究者深入探讨。
参考
- https://jalammar.github.io/illustrated-transformer/
- https://mp.weixin.qq.com/s/RLxWevVWHXgX-UcoxDS70w
- https://blog.csdn.net/qq_40176087/article/details/102471240?spm=1001.2014.3001.5506
- https://blog.csdn.net/qq_41664845/article/details/84969266
- https://zhuanlan.zhihu.com/p/69290203