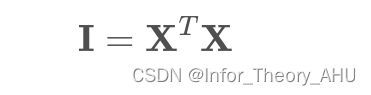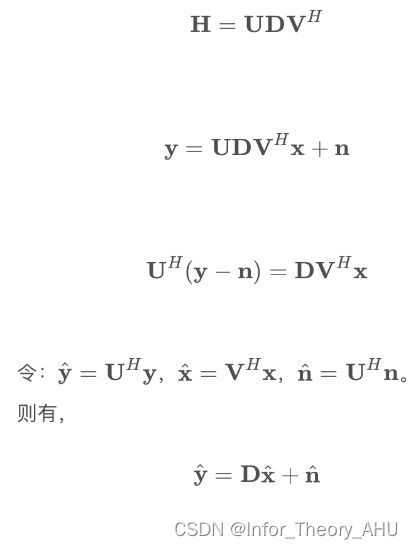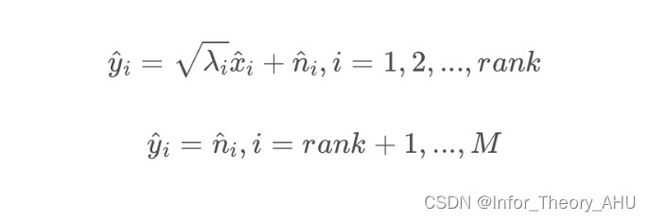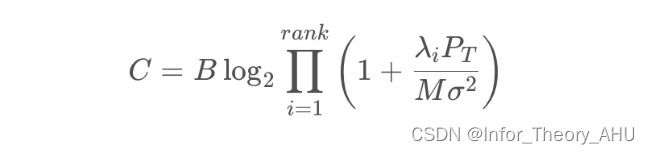P02014233梁园信息论作业

2. 在面临香农公式被逼近极限，未来无线通信会朝着哪些方向发展？结合信息论谈一下自己的见解

信息理论的基础-香农信息论构建了现代信息大厦的根基，建立了信息度量、压缩、传输的基础理论体系。同时也对通信传输中的极限提出了从语义层面出发的解决方案，迈入数智化时代，我们进入到万物感知、万物互联的智能社会，新的生产和生活模式也在不断的崛起中，这些都与七十年前香农时代发生了根本性的变化。随着 5G技术的快速发展，几乎达到了香农定理的极限。计算与通信演化的方向朝量子计算、DNA存储、语义通信的方向延展。利用语义通信来解决信息传输的存储与效率等问题，运用量子计算的特质来并行执行庞大的计算任务。探索这些新的信息传递与处理模式，可以把信息的传递延伸到更加广阔的未知地带，如深海通信、深空通信、人体网络和分子网络等。这些研究的方向都为未来提供了新的增长与创新空间。在通信行业内，语义通信也开始被看重，通信界巨头、大公司都在基础理论方面开始探索。而在这些先行者的步伐中，未来我们也会看到AR、VR的实时常态化使用，大量智能体间信息的传输会更快更准确。

3. 在通信系统中，除了常见的高斯白噪声还有哪些噪声会对我们无线传输造成影响？

对无线传输造成影响的噪声还包括以下几大类

1. 外部噪声，具体分为以下几类：1近地噪声2太阳系噪声3宇宙噪声          

其中近地噪声·对无线通信系统的影响最大

1. 内部噪声，具体分为以下几类：1天线噪声2馈线噪声3收发开关噪声4前端低噪声放大器噪声5前端其他放大器噪声

4. 请简述MIMO信道的应用场景，举例说明针对MIMO信道容量的主要结论性成果，并给出推导过程

（1）应用场景

MIMO信道的应用场景包括空分复用、波束复形、双流波赋形

空分复用中无线信号在密集城区、室内覆盖等环境中会频繁反射，使得多个空间信道之间的衰落特性更加独立，从而使得空分复用的效果更加明显

波束赋形也叫波束成型或智能天线，在3G技术中已经得到广泛应用。通过对多根天线输出信号的相关性进行相位加权，使信号在某个方向形成同相叠加，在其他方向形成相位抵消，从而实现信号的增益。

双流波束赋形正是将波束赋形和空分复用结合起来，扬长避短的一种方案。

（2）Massive MIMO，目前是5G的一项关键技术。那么求解它的信道容量，对于我们研究它的属性尤为重要。今天，我们就求算一下信道容量。（奇异值分解法）

在通信系统中我们学到信道容量的一个计算式：

C = B l o g 2 ( 1 + S N R ) C=Blog_2(1+SNR)

C=Blog 2 (1+SNR)

 

其中B BB是带宽，S N R SNRSNR是信噪比，C CC是信道容量。

那么其实我们就是需要求解S N R SNRSNR。

假设M个接收天线，N个发送天线，那么MIMO模型的表达式如下：

y = Hx + n

y=Hx+n

 

其中， y是M × 1输出的信息， H是一个只能被接收机感知的矩阵，x是输入信息的N×1列向量， n是AWGN噪声组成的M×1列向量。

先了解一下奇异值分解（SVD）：

SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。那么我们定义矩阵H的SVD为：

其中U是一个M × M M\times MM×M的矩阵， D是一个M×N的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值， V是一个N × N的矩阵。U和V都是酉矩阵，即满足：

那么，考虑使用奇异值分解法处理H矩阵，得到：

令奇异值为 λ i，最多 r a n k ( H ) = min ( M , N ) 个非零奇异值，那么接收信号为：

由上述可知，MIMO其实是rank个平行的等效子信道组成的。对单个信道进行叠加得到

即MIMO信道的最终容量

6. 简述LZ编码原理，并举例说明[按照书中例5-10的条件，若输入信源符号序列U=(abbabaabbabab）]则对应的输出编码是什么？

LZ编码是一种由变长到定长编码，是基于字典的通用编码方案，算法与信源统计特性无关。

LZ编码步骤：

第一步：将信源输出序列分成各不相同的码段，尽可能取最短码段且各段不相同。

第二步：将第一步分好的各码段作为字典内容，码段的序号作为字典索引。

第三步：编码，新的码段是前面出现过的码段与新的信源输出的拼接。