线性分类器学习笔记
本篇主要整理自北邮鲁鹏老师的《计算机视觉与深度学习》课程资源可在B站上搜到。
1 前言
相关课程推荐：
图像包含了三维场景的结构信息和语义信息。视觉识别中与图像分类任务相关的任务有很多，其中比较典型的包括目标检测、图像分割、图像描述、图像生成等。
深度学习三要素：算法、算力、数据
常见神经网络：全连接神经网络、卷积神经网络、循环神经网络、变分自编码网络、生成对抗网络等
2 图像分类
图像分类任务是计算机视觉中的核心任务，其目标是根据图像信息中所反映的不同特征，把不同类别的图像区分开来。
图像分类：从已知的类别标签集合中为给定的输入图片选定一个类别标签。
图像分类任务的难点：跨越“语义鸿沟”建立像素到语义的映射、拍照视角的影响、光照、尺度、遮挡、形变、背景杂波、类内形变、运动模糊、类别繁多
数据驱动的图像分类方法：数据集构建、分类器设计与学习、分类器决策
分类器的一般设计流程如下：
图像表示：像素表示、全局特征表示（如GIST）、局部特征表示（如SIFT特征+词袋模型）
常见分类器： 近邻分类器、贝叶斯分类器、线性分类器、支撑向量机分类器、神经网络分类器、随机森林
损失函数：0-1损失、多类支撑向量机损失、交叉熵损失
优化方法：一阶方法——梯度下降、随机梯度下降、小批量梯度下降，二阶方法——牛顿法、BFGS、L-BFGS
图像类型：二进制图像、灰度图像、彩色图像
3 线性分类器
本节介绍的线性分类器流程如下：
线性分类器的优点：
- 形式简单、易于理解
- 通过层级结构（神经网络）或者高维映射（支撑向量机）可以
形成功能强大的非线性模型
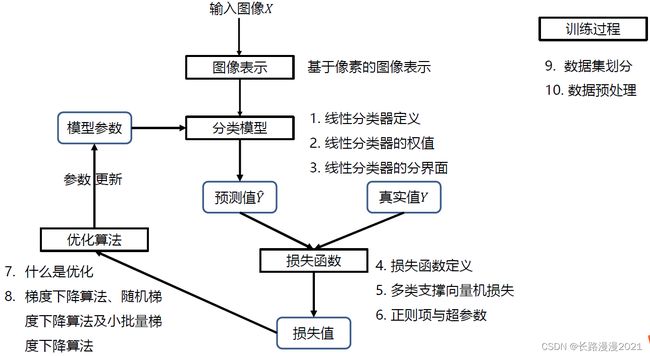
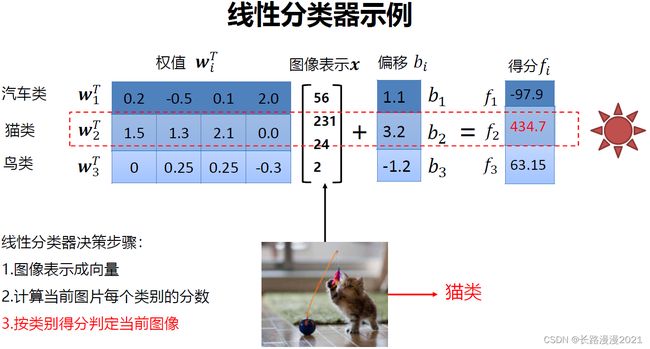
线性分类器是一种线性映射，将输入的图像特征映射为类别分数。第 i i i个类的线性分类器：
f i ( x , w i ) = w i T x + b i ， i = 1 , ⋯ , c f_i(x, w_i)=w_i^Tx+b_i，i=1,\cdots,c fi(x,wi)=wiTx+bi，i=1,⋯,c
x \pmb{x} xxx代表输入的 d d d维图像向量, c c c为类别个数， w i = [ w i 1 ⋯ w i d ] T \pmb{w}_i=[w_{i1} \cdots w_{id}]^T wwwi=[wi1⋯wid]T为第 i i i个类别的权值向量， b i b_i bi为偏置
线性分类器输入为特征向量。线性分类器的决策规则：计算当前图片每个类别的分数，即：
如果 f i ( x ) > f j ( x ) , ∀ j ≠ i f_i(x)>f_j(x), \forall j \not= i fi(x)>fj(x),∀j=i，则决策输入图像 x x x属于第 i i i类。
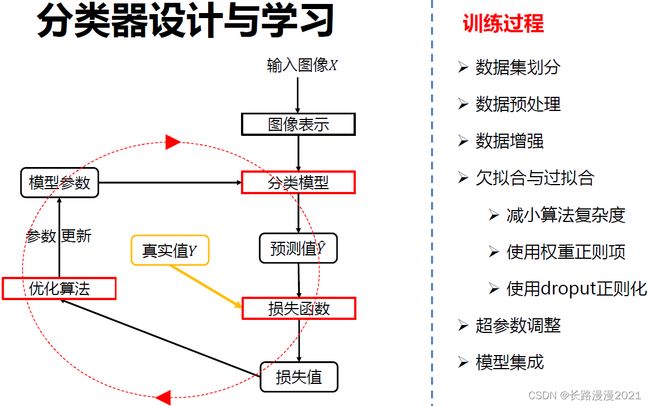
如何衡量分类器对当前样本的效果好坏？那自然是要损失函数，损失函数搭建了模型性能与模型参数之间的桥梁，指导模型参数优化。
- 损失函数是一个函数，用于度量给定分类器的预测值与真实值的不一致程度，其输出通常是一个非负实值。
- 其输出的非负实值可以作为反馈信号来对分类器参数进行调整，以降低当前示例对应的损失值，提升分类器的分类效果。
问题：假设存在一个 W W W使损失函数L=0，这个 W W W是唯一的吗？
答：不唯一，因为 W 2 W_2 W2同样有 L = 0 L = 0 L=0，应该如何在 W 1 W_1 W1和 W 2 W_2 W2之间做出选择？所以下面引出正则化损失。
接下来就是参数优化，参数优化是机器学习的核心步骤之一，它利用损失函数的输出值作为反馈信号来调整分类器参数，以提升分类器对训练样本的预测性能。
损失函数为：
L = 1 N ∑ i = 1 N L i + λ R ( W ) L = \frac{1}{N}\sum_{i=1}^{N}L_{i} + \lambda R(W) L=N1i=1∑NLi+λR(W)
损失函数是一个与参数 W \pmb{W} WWW有关的函数，优化的目标就是找到使损失函数达到最优的那组参数 W \pmb{W} WWW。直接方法，求导数为0并解出封闭解。通常， W \pmb{W} WWW形式比较复杂，很难从这个等式直接求解出 W \pmb{W} WWW！此时，就该梯度下降法闪亮登场。
梯度计算的两种方式：
- 数值梯度: 近似, 慢, 易写
- 解析梯度: 精确, 快, 易错
求梯度时一般使用解析梯度，而数值梯度主要用于解析梯度的正确性校验（梯度检查）。
梯度下降: 利用所有样本计算损失并更新梯度，当N很大时，权值的梯度计算量很大！此时可以使用随机梯度下降法，每次随机选择一个样本 x i x_i xi,计算损失并更新梯度。但是，单个样本的训练可能会带来很多噪声，不是每次迭代都向着整体最优化方向。于是，可以使用小批量梯度下降法。
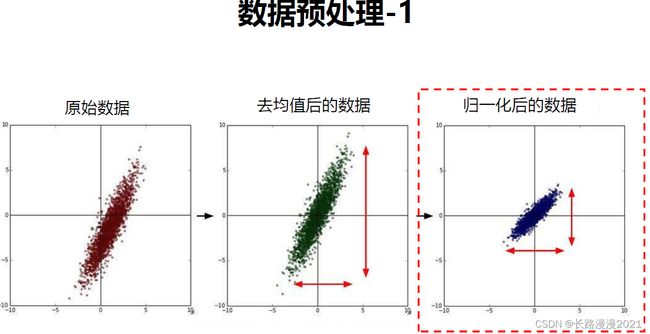
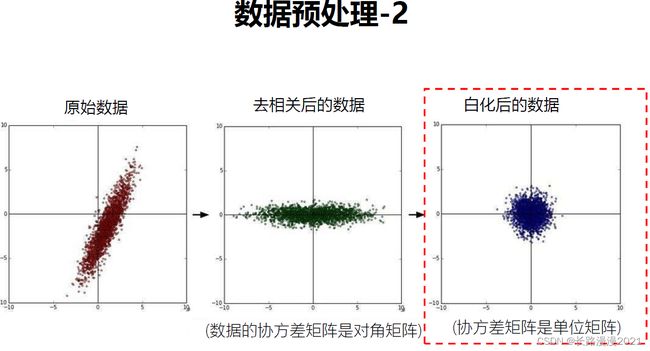
数据集通常划分为，训练集、验证集、测试集，运用机器学习传统方法的时候，一般将训练集和测试集划为7：3；若有验证集，则划为6:2:2。训练集用于给定的超参数时分类器参数的学习；验证集用于选择超参数；测试集评估泛化能力。
问题：如果数据很少，那么可能验证集包含的样本就太少，从而无法在统计上代表数据。
这个问题很容易发现：如果在划分数据前进行不同的随机打乱，最终得到的模型性能差别很大，那么就存在这个问题。而K折验证与重复的K折验证就可以解决该问题。
数据预处理，下图演示了两种常用数据预处理的方式：
