程序员的数学修养
缘起
原本，数学并不是一个职场热词。
直到人工智能的第三次高潮来临，传说中“做算法”七八十万的起步价和平均几百万的年薪刺激到了大众的神经，对大学数学课基础内容的重视才在程序员这个小众群体中成为话题。
不过可惜的是，成为话题并没有造成程序员批量重温（或重学）大学数学课的结果，而是导致很多人因为对数学的畏惧，而放弃了进军 AI 领域。
到底数学是不是 AI 的拦路虎？
如果不做 AI 相关的研发工作，程序员还需要加强数学修养吗？
如果连程序员也不打算当，普通人还有必要再学数学吗？
本 chat 主要是针对上面三个问题来进行探讨。
带着这些问题，先来看看：我们从小到大，到底学了多少数学——
我们系统地学过数学吗？
从小学一年级开始，主课里就有数学课。中小学十二年，大学如果是理工科的话最少再学两年，文科也要再学一年，那么也就是学了十三四年的数学。
但是，咱们这些非数学专业的毕业生，确定系统地学习过数学吗？
或者这么问：你能给出数学学科最粗浅的体系架构吗？（只要给出数学领域的几个大类和各类中的一级子类就可以。）
数学研究领域的划分
下图是一张数学地图（Math Map）：
在这里插入图片描述图中黄底的矩形框标识出了划分的三大类：
数学基础（不是基础数学）
纯数学
应用数学
其他矩形框标志了 2-3 个不同级别的子类。
这里面，你认识多少细分领域呢？
上图看起来有点，另找了一张和上图基本一致的数学领域分类导图（见下图）。在这张导图中，笔者用灰色椭圆框标志出了咱们学习过的领域：
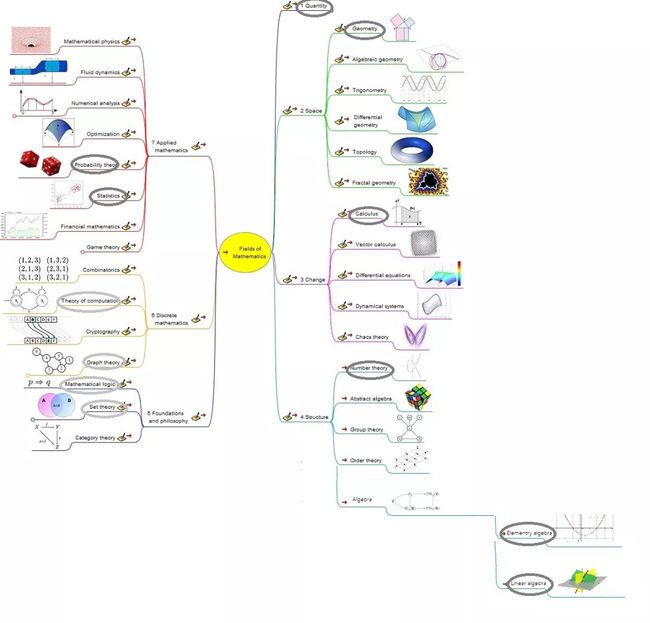在这里插入图片描述
注意：上图中框了椭圆的领域只是说我们学习过其中的部分内容，而不是说我们真的把那个子领域的都学透了!
如果不是计算机专业的同学，有可能连上图中浅灰色框住的部分都没学过。
即使是从这样一张并不严谨的导图中，都不难看出，我们其实根本没有系统性的学习过数学。
面向应用的碎片化学习
小学六年，工作日每天都要上数学课，但是我们到底学了什么呢？不过就是算数规则和极少量的数论内容而已——在上面导图中，满打满算也只能圈两个椭圆。
六年之功，沧海一粟而已。
当然了，小学数学虽然内容少，却是真的可以在实际生活中用到：我们看时间、算价格、计利息、掌握配方配比（比如烤蛋糕的配方)……都能用到小学的内容。
因此，基本上不会有人认为小学数学无用。
上了中学之后，小学单一的"数学“分成了代数和几何，我们开始学解方程（如今这部分有些内容已经迁移到小学了）；学各种函数——函数的表达式、图像和性质以及函数求解；学各种形状的性质、定理、定律……
到了大学，数学分的科就更多了：数学分析、概率统计、线性代数、离散数学，等等……
不过，好像这些东西，在日常生活中根本就用不到。
如果不是毕业以后想入行 AI，恐怕大多数人对大学数学的印象还基本停留在:
“学了能用来买菜吗？”
“（大学专业）学数学的除了当数学老师，还能干嘛？”
AI 技术岗，学数学的必要性
关于 AI 技术岗位学习数学的必要性我们不再长篇大论了，来看一个具体的问题吧：
虽然至今深度神经网络的最优化问题仍然缺乏理论基础，但各式各样针对训练、推理（预测）和数据的技术却层出不穷。
近几年新兴起了联邦学习（Federated Learning）的概念。
联邦学习是一种模型训练的方法，这种方法训练出的模型“兼具百家之长”（训练数据来自多家企业或组织）的同时，又保证“各家的家私秘而不宣”（其中任何一个数据提供方无须向其他提供方公开自己的数据）。
比如，AB 两家公司应用联邦学习联合训练一个模型，这两家各自设置一个训练环境，分别提供自己的数据，然后启动训练过程。
这个训练中的模型会“分身”到两家的训练环境中去，然后再把分别的训练结果汇总在一起。
最终被训练出来的模型，因为有两家提供的数据，所有适应性比只用一家数据要强，但整个训练过程中，各家的数据都确保不会被另一家看到。
这是怎么做到的呢？是模型先在 A 家训，然后训成的“半成品”再去 B 家训吗？如果是这样的话，那就变成迁移学习（Transfer Learning）了。
联邦的学习是在 AB 双方同时进行的，在训练的过程中，两个训练环境不交换数据，却要交换梯度的中间结果。
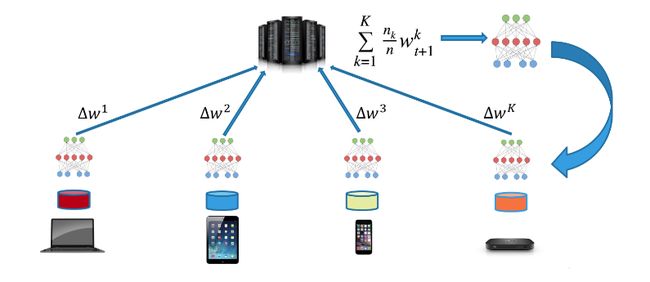在这里插入图片描述
梯度是什么？
什么函数的梯度？
梯度有什么用？
在训练过程中随时交换了梯度和在一方数据集上训练完成后再到另一方去训练有什么不同？
……
这些问题，对于具备数学基础的同学很好理解。而对于没有数学基础的人，能解释清楚吗？
没有数学知识，也就不能真的掌握机器学习/深度学习的模型函数、目标函数、最优化过程和算法原理。
在这种情况下“做算法”，最多只能是把用别人已经构造好的网络结构或者算法程序在自己的数据上运行一遍。别说网络或者算法本身，就是改变数据特征值的提取方式都未必能做到。
这样的人，比自动调参程序又强在哪里呢？
为什么大学数学课学了好像没学过？
其实，AI 需求的那些数学知识点（后面会具体列举），一般大学理科毕业生在大学里面都是学过的。
只不过，一种普遍存在的现象是：等到毕业了几年之后，回头再看这些早就学过的东西，却好像完全没学过一样。
怎么会这样呢？可能有两种情况:
【情况-1】 当时就没学懂；
【情况-2】 当时懂了，但是过后忘了。
如果是【情况-1】，那没办法，只能从头学一遍了。
但即使是重学了一遍，而且真的都学懂了，学完以后还是有可能很快就给忘了！
对大多数人而言，【情况-2】是早晚都要应对的问题。
如果你遭遇过“遗忘了曾经学懂过的知识”这种情况，那么请回顾一下：你是仅仅忘记了知识本身呢？还是把表述知识的符号系统也给忘了?
说得更明白一点，再打开大学数学课本，就算具体的定理引理推理公式法则方法全都忘了，里面那些非文字符号表达什么意思，你还记得吗？
说说符号系统
符号系统是一个我们有必要专门说说的话题。
在说符号系统之前，我们其实该问一个问题：“什么是知识？”
什么是知识
对于这个问题可以有各种从不同维度深入的探讨，我们不是哲学家，对于形而上的争论也不感兴趣，只想从实用角度出发，以更加高效地学习为目的来理解什么是知识。
从这个角度而言知识其实可以分成两大类：
I. 人为定义的符号系统。
II. 用一套或者多套人为定义的符号系统对客观事物进行的描述。
注意: 对客观事物的描述才属于知识，所有主观的观点、想象、感受、情绪、体验都不属于知识范畴！
II 是目的，I 是手段（当然，I 并不仅仅可以表达 II，也可以用来表达主观的情感和观点）。
手段是达到目的的途径
目的当然比手段重要，但是很多时候，如果没有手段，目的根本就不可能达到！
就学习这件事情而言，确实有些内容的学习，无需人工符号系统，仅仅展示客观过程就可以了——比如各种教人做家务、小手工的短视频。
但一遇到比较复杂，或者有一定理论性质的内容，就不得不借用符号系统了。
人类定义的符号系统有很多套，比如：自然语言、数学符号、五线谱、摩尔斯码、旗语、程序设计语言等等。
有些历经长久历史而形成，由于使用的多样性，可能会造成部分规则不清晰或者有歧义的情况——最典型的就是自然语言。
但也有一些符号系统是建立在严格逻辑基础上，由少数精英人才集中制定的。这种系统通常具备严格和严密的特征，对它们的用法是可以有绝对的对错之分的——数学（尤其是高等数学）符号，就属于这类系统。
很多数学问题，之所以让人头大，其实并不是真的有多难，而是：i）符号系统比较复杂，ii）运算繁复，或者 iii）运算所表达的物理意义多样。
而掌握 ii）和 iii）的前提是掌握 i）。
数学符号
学习高等数学，第一个任务就是掌握其符号系统！
高等数学的领域很多，就我们急需的几个子领域而言，微积分的符号相对多一些也“各色”一些：
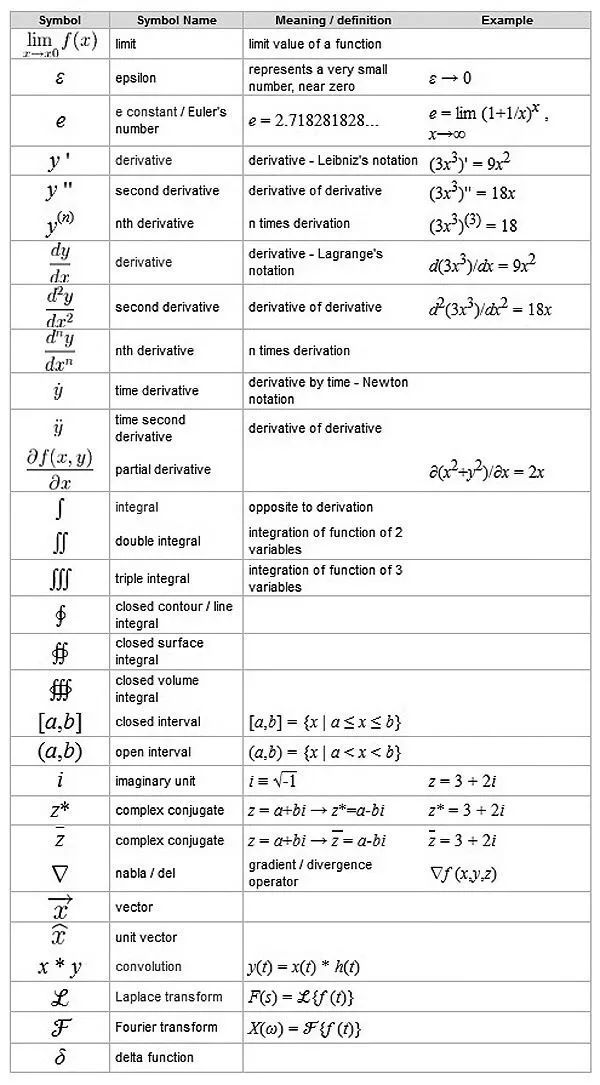在这里插入图片描述
线性代数关键是矩阵和向量的表达：
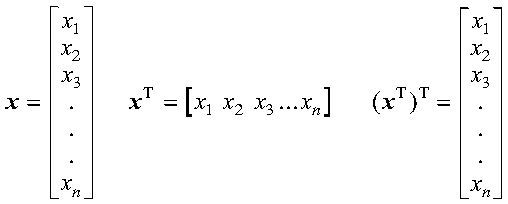在这里插入图片描述
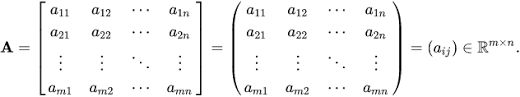在这里插入图片描述
注意：矩阵和向量的表示规则本身清晰，也不算复杂。不过这种表示如果出现在网页上需要特殊的编辑。
有时候，有些页面不支持 Latex，也可能是编辑者偷懒，没有用上图这样的二维方式表示矩阵或向量，而是比较随意地用 xij 之类的不规则符号展示。这种情况下就需要读者分辨清楚。
必不可少的背诵
了解清楚符号含义是必要条件，学习任何符号系统都有很大的背诵成分。
我们在读小学的时候，花费了大量的时间用来识数、认字，整个过程漫长且不乏痛苦。掌握 3000 汉字大致消耗了六年时间。
十个阿拉伯数字和算术运算符号虽然数量很少，但练习最简单的加减乘除也得要三四年功夫。
我们现在能够自如地阅读母语文本，能够熟练地做简单算术运算，是曾经真的投入了很多时间和精力在背诵和反复练习这样的“拙功夫”上，才达到的结果。
高等数学的符号系统一则比初等数学复杂，二则，我们实际学习这套符号系统的时间要短得多。
一般理科非数学专业也就本科前三年学数学，三年若干套复杂符号 vs 六年一套算数符号，如此悬殊的任务量投入比，大学学的内容“过后就忘”也是难免的。
更何况，小学数学真的买菜要用，而大学数学在一般性质的日常工作中很少触及。实际演练上的差距造成了大学数学“学过了好像没学一样”，也很正常。
之所以关于一个符号系统说了这么多，笔者是希望：
正视我们在中小学基础教育中的收获，不要动不动自以为“我在学校里什么都没学到，所有工作中会的都是自学的”。
只要你是从学校里学的认字识数，你就不是什么都没学到。反之，如果几千个汉字都是你自学的，那么相信你自学大学数学也没问题，就别抱怨了，马上买套课本开始学吧！
别怕高等数学，其实你一直觉得自己学不会未必是因为这些知识理论本身多么难，很可能只要是因为你没把那套表达符号记住。
拿出小学抄写生字的勤奋和勇气来，学会这些希腊字母和扭曲“花纹”！常用的符号/字母还不到 100 个，比汉字可少多了。
大家能够在学习的过程中主动地将事实、原理、方法本身和它们的描述区分开来。
而不是眉毛胡子一把抓，不得要领，最终导致在一团混乱的困难中觉得无所适从而放弃。
从 AI 出发，看大学数学
毕竟，对于大多数同学，不管遗忘大学数学的原因是什么，重新学一遍是免不了的。
我们先来看看到底要学什么：
AI 技术岗必备高等数学知识点清单
AI 技术岗所要求的高等数学知识，大致可以分为四个方面：微积分、概率统计、线性代数，和最优化理论。
每个分领域都至少是一本书（也可以是一摞书）。我们在这里暂且抽取和机器学习、深度学习直接相关的部分，给大家做一下聚焦：
【微积分】
基础概念（极限、可微与可导、全导数与偏导数）：只要学微积分，就必须要明白的概念，否则后面什么都无法继续学习。
函数求导：求导是梯度的基础，而梯度是 AI 算法的基础，因此求导非常重要！必须要搞清楚概念，并学会常见函数的导函数求法。
链式法则：符合函数求导法则，反向传播算法的理论基础。
泰勒公式和费马引理：这两者也是梯度下降法的基础组成，重要程度与求导相同。
微分方程及其求解：很重要，是部分机器学习模型求解的必备知识。
拉格朗日乘子法和对偶学习：理解 SVM/SVR 的理论基础。SVM/SVR 作为机器学习模型的常用“中坚力量”，其重要程度不言而喻。
【概率统计】
简单统计量（个数、最大值、最小值、中位数、均值、方差）及其物理意义：概率统计的概念基础。
随机和抽样：随机——概率统计成立的基础；抽样——统计的方法。
频率和概率，以及概率的基本概念：搞清什么是概率，它和频率的区别与联系。
几种常见的概率分布及公式（平均分布、二项分布、正态分布……）
参数估计：只知道大致的分布，不知道具体的参数怎么办？没关系，我们可以根据估计一下。其中最重要的是极大似然估计。
中心极限定理：如果不知道某事物的概率分布该怎么办?没关系，就当它符合正态分布好了。可是为什么能这样近似呢?因为我们有中心极限定理呀。
假设验证：到底假设得对不对呢？我们根据样本来验证一下。
贝叶斯公式：太重要啦！是它使得我们可以根据先验概率来预测后验概率。而朴素贝叶斯公式自己就是朴素贝叶斯模型本身啊。
回归分析：想想那么多名字里有“回归”的模型吧!
状态转移网络：概率链、隐马尔可夫模型和条件随机场。
【线性代数】
向量与标量：用向量和标量表示事物特征的差别是什么？
向量空间，向量性质及向量的几何意义：所谓高维低维指的是什么？同一个向量能否存在于不同的向量空间里？向量的移动、转向和拉伸是如何做到的？
线性函数：什么是线性函数，它具备怎样的性质？
矩阵和矩阵运算：矩阵出现的目的是什么？掌握矩阵的基础运算（与常数/向量/矩阵的加法和乘法）。
特殊矩阵（方阵、实对称矩阵、（半）正定/负定矩阵等）及其性质：根据不同的性质，我们可以划分出哪些特殊矩阵，它们都有哪些特殊性质？
特征值和特征向量：定义、性质，以及特征值求解。
用矩阵求解微分方程。
正交：什么是正交？函数的正交，向量的正交，和超平面的正交分别是如何形式化表达的，又具备怎样的物理意义。
【最优化方法】
凸函数与极值：搞清楚什么是凸函数，凸函数与极值的关系，极值和最值的关系等。
注意：国内不同教科书对于“凸”的定义存在不一致的情况，有些书上把其他书上说的“凸函数”叫做“凹函数”。
直观而言，我们一向说的“凸函数”是那类一维自变量情况下看起来像个“U”，二维自变量下像个碗的那种函数。
最优化：什么是最优化问题？什么是最优化方法？无限制条件和有限制条件下的最优化方法基本原理分别是什么？
梯度下降法：最基础最常用的最优化方法，以及其他若干最优化方法的基础，务必全面掌握。
其他最优化算法：了解其他一些常用最优化方法，例如，牛顿法、共轭梯度法、线性搜索算法、模拟退火算法、遗传算法等。
“以人为轴”学数学
学什么是蛮清晰的，关键是怎么学？
或者，更直接点说：有没有办法能够轻松愉快不累且高效地学习人工智能（机器学习/深度学习）领域要用到的数学知识呢？
这里推荐一种笔者在探索中逐步发现的，简单直接又有些趣味的方法：以数学家为主线学习高等数学知识——也就是，“以人为轴”学数学。
什么叫“以人为轴”？我们先来看看下面这些画像吧：
在这里插入图片描述
能认出几个？
他们分别是（从左到右从上到下依次）：牛顿、高斯、贝叶斯、费马、泰勒、拉格朗日、拉普拉斯、傅立叶，和伯努利。
说实话，现在全球数以千万计的 AI 技术人员真应该把这些大佬供起来，说咱们的饭碗都是他们赏的也不为过。
牛顿大神发明了微积分；
辅之以费马引理、泰勒公式，奠定了如今一切 AI 最优化算法工程实现的理论基础。
拉格朗日乘子法为限定条件下多元函数的最优化问题提供了解法。
数学王子高斯在概率论和线性代数领域的非凡贡献不胜枚举，仅仅高斯分布一项就堪称概率论之抗鼎模型。
贝叶斯让我们可以用既往经验预测未来。
伯努利家族不仅在概率论领域贡献颇丰，就连他家二弟卖给洛必达的“洛必达法则”亦是求解具有不定型的极限的不二法门。
拉普拉斯算子于微积分和线性代数而言都是非常重要的基石。
傅立叶变换在时域信号和频域信号之间的桥梁作用成就了整个语音领域。
还有下面这位：
在这里插入图片描述
莱布尼茨与牛顿分别独立发明了微积分，他提出的符号系统一直沿用至今。他同样是西方二进制算数体系的提出者和线性代数的重要奠基人。
当然，无论微积分、概率统计还是线性代数，都不是在一日之内形成的学科，都经历了数百年乃至上千年大量人类顶级头脑的思考和探索，对其做出贡献的数学家灿若繁星。
对照我们亟待掌握的知识点，以这些理论的提出者为基点，沿着数学史学习之，并同步了解数学发展的进程。顺便还可以以大神们之间的交往和恩怨等八卦作为润滑剂。
如此一路学来，既多了许多趣味，又能追本溯源，了解到这些理论提出的现实背景（例如：物理学的发展及其对数学工具的需求）。
在学理论的同时了解这一理论最初的作用域和当时解决的实际问题，对于我们理解其中各类概念的物理意义有着极大的帮助。
由于篇幅有限未能展示全部内容，
感兴趣的同学可以通过二维码继续阅读
▼
这两年机器学习、深度学习热起来之后，很多程序员开始担心自己的数学水平，怕高等数学学得不够好，不能成功转型做算法。其实，这话要两说着。
问大家几个问题：
高数、概率、线代这些大学数学课的知识现在无法运用，是忘了，还是当时就没学明白？
中小学的数学课内容，又真的学透了吗？
不做 AI 算法，编程的工作就不需要数学知识了吗？
如果已经做了一段程序员，工作却丝毫没有感觉到反刍数学知识的必要，会不会是工作太浅表了？
如果不做程序员，数学除了买菜，还能做什么？
从来没有学习过高等数学的人，有没有可能在生活中运用微积分、概率论的原理呢？
本 Chat 在列举程序员数学修养规划路径的同时，力图回答这些问题。
点击「阅读原文」，也可以哦