（RL强化学习）A2C PPO DDPG理论和具体算法流程

ps:笔记参考了

• 强化学习–从DQN到PPO， 流程详解
• 白话强化学习

AC

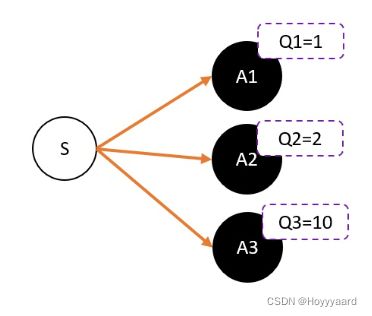
• Actor：输入状态S 输出策略选择动作

• Critic：负责计算每个动作的分数

• TD-error

  • TD-error就是Actor带权重更新的值

  • Critic只需要最小化TD-error以此更新网络

  • AC中的C估算的是V值而不是Q值

  • 假设估算Q值
    

    • 假设随机采样到A1 Critic估算出Q1 那么Actor就会更新A1的权重 使A1的权重不断升高 掉入正数陷阱
    • 但是此时最应该做的是提高A3或者削弱A1
    • 故只需要使Q减去一个baseline就可以了

  • V值是Q值的期望 故可以用Q值减去V值 就得到有正有负

  • 

  • 故TD-error = gamma * V(s’) + r - V(s)

• 算法流程

1. 定义两个network：Actor 和 Critic

2. 进行N次更新。

3. 1. 从状态s开始，执行动作a，得到奖励r，进入状态s’
   2. 记录数据。
   3. 把St，St+1输入到Critic，根据公式： TD-error = gamma * V(s’) + r - V(s) 求 TD-error，并缩小TD-error
   4. 把St输入到Actor，计算策略分布 并用TD-error进行PG 。

PPO（proximal Policy Optimization）

• 重点：

  • 用网络求解连续动作型问题；

  • 进行N步更新；

  • 重要性采样及PPO网络的更新学习。

• 用网络求解连续性动作

  • 网络不在输出具体的策略（action），而是输出策略的分布；比如正态分布则输出均值和方差，然后进行采样得到策略（action）

• N步更新（TD（n））

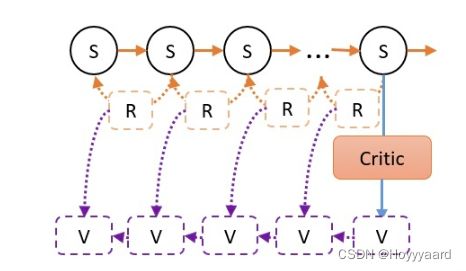
  • AC中采用的是TD（0）：也就是说没一个step更新以此网络
  • PPO使用的是N步更新，让agent先走N步，Critic计算最后一步的V，根据V_St = r + GAMMA * V_St+1的方式反算出前N-1 步每一步的V后进行N次更新

• 重要性采样

  • PPO中的重要性采样用在了Actor中网络的循环更新，也是PPO中可以称为运用了off-policy的点；
  • 在N步采样的时候有两个参数相同的Actor网络：A-old，A-new，N步采样后需要对Actor网络进行循环更新网络参数，第一次更新A-new的时候sample的data服从A-old和A-new的分布，当第二次更新的时候（一二次更新之间不采样）A-new的分布和sample的data的分布已经不相同，故需要用到important sampling

• 算法流程

1、将环境信息s输入到actor-new网络， 得到两个值， 一个是mu， 一个是sigma， 然后将这两个值分别当作正态分布的均值和方差构建正态分布(意义是表示action的分布)，然后通过这个正态分布sample出来一个action， 再输入到环境中得到奖励r和下一步的状态s-new_，然后存储[(s,a,r),…], 再将s-new输入到actor-new网络，循环步骤1， 直到存储了一定量的[(s, a, r), …]， 注意这个过程中actor-new网络没有更新。

2、将1循环完最后一步得到的s-last输入到critic网络中， 得到状态的v-last值， 然后计算折扣奖励：

R_St = r + GAMMA * V_St+1， 得到R = [R[0], R[1],…,R[t],…,R[T]]，其中T为最后一个时间步。

3、将存储的所有s组合输入到critic网络中， 得到所有状态的V_值， 计算At = R – V_

4、求c_loss = mean(square(At )), 然后反向传播更新critic网络。

5、将存储的所有s组合输入actor-old和actor-new网络， 分别得到正态分布Normal1和Normal2， 将存储的所有action组合为actions输入到正态分布Normal1和Normal2， 得到每个actions对应的log(prob1)和log(prob2)， 然后用2除以1得到important weight, 也就是ratio。

6、采用PPO2的方式计算a_loss = mean(min((ration* At, clip(ratio, 1-ξ, 1+ξ)* At))), 然后反向传播， 更新actor-new网络。

7、循环5-6步骤， 一定步后， 循环结束， 用actor-new网络权重来更新actor-old网络

8、循环1-7步骤。

DDPG（deep deterministic policy gradient）深度确定性策略梯度算法

• 简介

  • 用于解决连续控制型问题的一个算法；PPO输出的是一个策略分布，DDPG输出直接一个动作
  • DDPG更接近DQN,DQN只解决了状态连续的问题没有解决动作空间连续的问题

    • 

    • DQN中需要根据S选择出一个Q值最大的action，要是用Q-table的方式则无法穷举状态 ，故使用NN输入S输出每个action对应的Q

    • DQN不能用于连续控制问题原因，是因为maxQ(s’,a’)函数只能处理离散型的

    • DDPG就是用一个NN代替maxQ(s’,a’)使只可以运用在连续控制

• DDPG中的actor，critic

  • 

  • critic：输入S 和 A 输出 一个Q值，更新方式用TD-error

  • actor：输入S 输出A 目标是A输入到critic中能够获得最大的Q值，故更新方式为gradient ascent（梯度上升）

• 和DQN一样，更新的时候如果更新目标在不断变动，会造成更新困难。所以DDPG和DQN一样，用了固定网络(fix network)技术，就是先冻结住用来求target的网络。在更新之后，再把参数赋值到target网络

​

• 算法流程

  

1、将环境信息s输入到actor eval网络， 输出为action， 将action输入环境， 得到奖励r和下一个环境信息s_， 存储当前环境s, 选择的action, 得到的奖励r这4个信息, 然后再将s_输入到actor eval网络， 循环步骤1， 直到存储了一定量的记忆[(s, a, r, s-new), …]， 注意这个过程中actor eval网络没有更新。

2、从第一步中存储的记忆中sample出部分[(s, a, r, s-new), …]

3、将sample出来的s全部输入到actor eval网络中得到action, 再将此action与s输入到critic eval网络中得到q值。

4、求a_loss = mean(q)， 反向传播更新actor eval网络

5、将sample出来的s-new输入到actor target网络得到action-new。

6、将sample出来的s-new和第6步得到的action-new一起输入critic target网络， 得到q-new值。

7、计算q_target = sample出来的r + gamma * q-new 。

8、计算c_loss = MSE(第3步的结果q， q_target) 。

9、通过c_loss反向传播更新critic eval网络

10、循环1-9步骤， 在一定步骤后更新actor target、critic target网络，更新方式为：

W(actor target) = W(actor eval) * μ + W(actor target) * (1- μ)

W(critic target) = W(critic eval) * μ + W(critic target) * (1- μ)

也就是说actor target、critic target网络权重只是小步幅更新。