论文阅读笔记——representation learning on graphs:methods and application
Hamilton W L, Ying R, Leskovec J. Representation learning on graphs: Methods and applications[J]. arXiv preprint arXiv:1709.05584, 2017.
文章目录
- 1. Introduction
- 2.Embedding nodes
-
- 2.1方法概述:encoder-decoder perspective
- 2.2 浅层嵌入方法 Shallow embedding approaches
- 2.3 based on deep learning
- 2.4 Incorporationg task-specific supervision
- 2.5 Extensions to multi-modal graphs
- 2.6 Embedding structural roles
- 2.7 Applications of node embeddings
- 3.Embedding subgraphs
-
- 3.1 sets of node embeddings and convolutional approaches
- 3.2 Graph neural networks
- 3.3 Applications of subgraph embeddings
- 4.Conclusion and future directions
-
- 4.1 Important open problems
1. Introduction
①图表示学习领域的主要挑战:找到一种表示或编码图形结构的方法,方便机器学习利用。从机器学习的角度来看,面临的挑战是没有直接的方法将有关图结构的高维非欧式信息编码为特征向量。
②关于图的机器学习的一个关键问题是:找到一种将图结构信息整合到机器学习模型中的方法。
③图表示学习的思想:将节点或整个(子)图作为点嵌入到低维向量空间中是映射。
目标:优化此映射,使嵌入空间中的几何关系能反映原始图的结构
④传统的图结构信息提取方法:人工选取的图的特征来统计信息(如度或聚类系数)——>缺点:普适性差、耗时。
⑤表示学习方法与以前的工作间的主要区别:它们如何处理表示图结构的问题。此前的工作将图结构表示视为预处理步骤,使用手工设计的统计信息来提取结构信息。而表示学习方法将该问题视为机器学习任务本身,使用数据驱动的方法来学习对图结构进行编码的嵌入。
2.Embedding nodes
2.1方法概述:encoder-decoder perspective
①encoder-decoder framework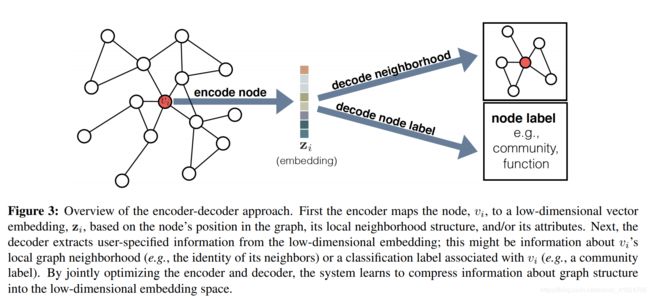
encoder:将每个节点映射为低维向量或嵌入
decoder:将学习到的关于图的嵌入解码为图的结构信息
encoder-decoder架构缺点:
a)encoder中参数不能共享
b)在编码过程中浅层嵌入不能利用节点属性
c)浅层嵌入方法本质上是transductive
“Transductive learning:unlabelled data is the testing datainductive learning:unlabelled data is not the testing data
在训练过程中,已知testing data(unlabelled data)是transductive learing
在训练过程中,并不知道testing data ,训练好模型后去解决未知的testing data 是inductive learing”
②按照以下四个组成部分,对节点嵌入方法进行分类:
1)A pairwise similarity function
2)An encoder function
3)A decoder function
4)A loss function

2.2 浅层嵌入方法 Shallow embedding approaches
①Factorization-based approaches:学习每个节点的嵌入。使学习的嵌入向量之间的内积近似于某种确定性的节点相似性度量
1)Laplacian Eigenmaps
2)Inner-product methods
②Random walk approaches
创新点:优化节点嵌入,使得倾向于在较短的随机游走中同时出现的节点具有相似嵌入
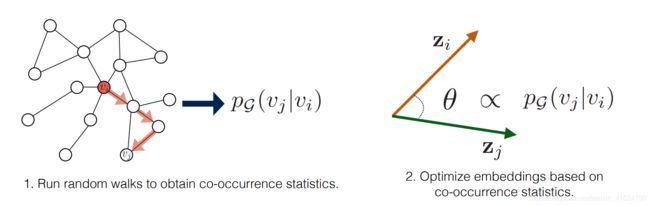
1)Deepwalk
2) node2vec
注:Deepwalk与node2vec的不同:a)使用了不同的优化和近似值计算公式中的损耗;b)node2vec允许灵活定义随机游走,而DeepWalk在图形上使用简单的无偏随机游走
3)Large-scale information network embeddings(LINE):LINE相较于Deepwalk和 node2vec也使用了概率解码器和损失,但明确的分解了一阶与二阶相似性,而不是将他们组合成固定长度的随机游走
4)HARP:Extending random-walk embeddings via graph pre-processing:引入一种成为HARP的“元策略”,用于通过图形预处理步骤改进各种随机游走方法
5)Additional variants of the random-walk idea
2.3 based on deep learning
与浅层嵌入的区别:基于深度学习的方法使用深度神经网络将图的结构直接合并到编码器算法中,即使用自动编码器压缩有关节点本地邻居的信息,如图
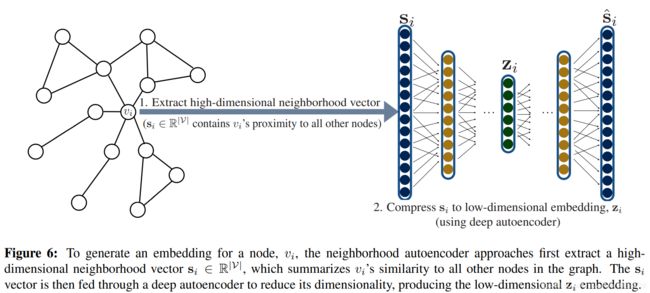
①neighborhood autoencoder methods
1)Deep Neural Graph Representations(DNGR)
2)Structure Deep Network Embeddings(SDNE)
DNGR和SDNE的编码器和解码器功能均由多个堆叠的神经网络层组成:编码器的每一层都减小了其输入的维度,解码器的每一层都增大了其输入的维度。
autoencoder方法面临的限制:a)自编码器的输入维数固定为|V|,这对于具有数百万各节点的图来说可能是非常昂贵的。b)自编码器的结构和大小是固定的,SDNE和DNGR是tranductive的,无法应对不断变化的图,也无法在图之间进行概况。
②neighborhood aggregation and convolutional encoders
具体思想:通过聚合来自其本领域的信息来生成节点的嵌入,如下图
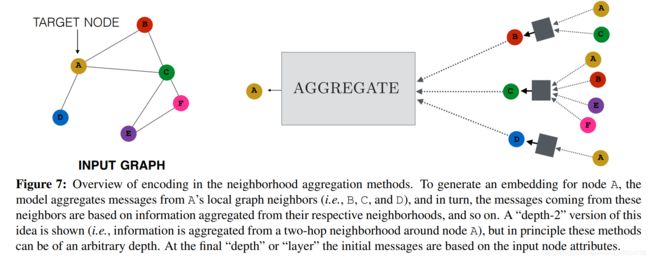
算法:

1)graph convolutional networks(GCN)
2)column networks
3)GraphSAGE
三种方法的主要不同之处在于执行汇总和向量组合的方式
2.4 Incorporationg task-specific supervision
2.5 Extensions to multi-modal graphs
①Dealing with different node and edge types
问题:以上的方法专注于无向图,但现实中的图往往具有复杂的多峰或多层结构,如:异构节点和边类型
——>解决方法:1)对不同类型的节点使用不同的解码器
2)使用特定于类型的参数扩展成对解码器
3)从异构图采样随机游走的策略,其中随机游走仅限于特定类型节点之间的过渡
②Typing node embeddings across layers
在某些情况下,图具有多个“层”,其中包含相同节点的副本(如图8 a)
——>可跨层共享信息
——>Ohmnet:将node2vec与一个regularization penalty 结合,regularization penalty将各层之间的嵌入联系在一起
——>有人进一步提出:利用图层之间的层次结构进一步扩展此(如图8 b)
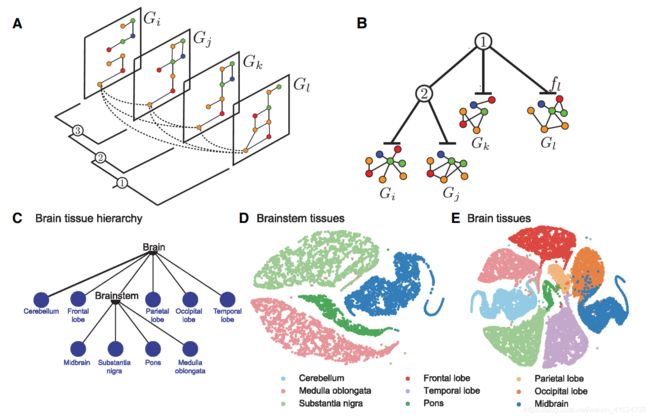
2.6 Embedding structural roles
①问题:以上的所有方法都是优化节点嵌入,使图中的附近节点具有相似的嵌入。但在许多任务中,更重要的是学习与节点的结构角色相对应的表现形式,而与它们的全局图位置无关。
②解决方法:
1)struc2vec
2)GraphWave
2.7 Applications of node embeddings
① Visualization and pattern discovery
② Clustering and community detection
③ Node classification and semi-supervised learning
④ Link prediction
3.Embedding subgraphs
子图的表示学习任务:将一组节点和边编码为低维向量嵌入。
graph kernels的设计定义了子图之间的距离度量,故其与子图上的表示学习密切相关。
3.1 sets of node embeddings and convolutional approaches
基本思想:将子图等同于节点嵌入集,使用卷积领域聚合思想为节点生成嵌入,然后使用其他模块聚合与子图对应的节点嵌入集。
对于以下的方法之间的主要区别在于:它们如何聚合与子图相对于的节点嵌入集。
①Sum-based approaches
通过将子图中的所有单个节点嵌入求和来表示分子图表示中的子图。
②Graph-coarsening approaches
采用了卷积方法,在图粗化层中,将节点聚合在一起(使用任何图聚类方法),并且聚合的节点嵌入使用逐元素的最大池合并。聚类后,新的较粗图再次通过卷积编码器输入,然后重复该过程。
③Further variations
1)使用“模糊“直方图而不是总和来聚合节点集
2)在节点上定义顺序,并使用此排序,将所有节点的嵌入连接起来,并通过标准的卷积神经网络将此连接的向量馈入。
3.2 Graph neural networks
图形卷积神经网络GNN:将图视为指定节点之间“消息传递”算法的支架,而不是从邻居那里收集信息。
3.3 Applications of subgraph embeddings
子图嵌入的主要用例是子图分类
4.Conclusion and future directions
4.1 Important open problems
①scalability
②Decoding higher-order motifs
③Modeling dynamic,temporal graphs
④Reasoning about large sets of candidates subgraphs
⑤Improving interpretability