数字信号处理实验十二 分段卷积
一、实验目的
1.学习分段卷积的概念及其应用。
2.掌握如何来实现分段卷积。
二、实验原理及方法
在某些场合下,可能要求将一个有限长度的序列与一个长度不定或相当长的序列进行线性卷积,若将整个序列存储起来再作大点数的运算,不但运算量大,而且往往时延也不允许并且在实际应用中,往往要求实时处理。在这些情况下,就要将长序列分段,每一段分别与
短序列进行卷积,即分段卷积。有两种方法:重叠相加法和重叠保留法。
1.重叠相加法
设序列h(n) 长为 M, x(n) 是长序列。这种方法是将 x(n) 分段,每段长与h(n) 接近设为 N₁,将每一段分别与h(n) 进行线性卷积,再将分段卷积各段重叠的部分相加构成总的卷积输出。
2.重叠保留法
这种方法在长序列分段时,段与段之间保留有互相重叠的部分,在构成总的卷积输出时只需将各段线性卷积部分直接连接起来,省掉了输出段的直接相加。
设序列h(n) 长为 M, x(n) 是长序列,将 x(n) 分段,每段长为 N₁,然后各段再往前多
取个 M − 1 样值,这样,取出的各段 xk (n) 长度为 N = N1 + M −1 。为了保证最前面的一段 x0
(n) 之长也为 N,取出开始的 N₁ 个样值之后,再在其前面补上 M − 1个 0。

三、实验内容
1.设 x(n) = 3n + 2(0 ≤ n ≤ 18) ,h(n) = {1, 2, 3, 4} ,按 N = 7 用重叠保留法计算线性卷积 y(n) = x(n) * h(n) 。
2.用重叠相加法( N = 7 )重复上面的计算,看结果是否相同?
参考流程图:
四、实验报告要求
1.简述实验原理及目的。
2.写出实验程序及结果,比较重叠保留法与重叠相加法及与直接线性卷积有无异同?
2.1
nx=0:18;
x=3*nx+2;
h=[1,2,3,4];
M=length(h);
nh=0:M-1;
y1=conv(x,h);
n01=min(nx)+min(nh);
n02=max(nx)+max(nh);
ny1=[n01:n02];
subplot(321),stem(nx,x,'.');title('x(n)');
subplot(322),stem(nh,h,'.');title('h(n)');
subplot(312),stem(ny1,y1,'.');axis([0,30,0,600]);title('线性卷积');
n=0:27;
x=[x,zeros(1,9)];
N=7;
L=N+M-1;
y=zeros(1,4*N);
for k=0:3
x1=zeros(1,L);
x1(4:10)=x(k*N+1:(k+1)*N);
if k~=0
x1(1:3)=x(k*N-2:k*N);
end
x1k=fft(x1,L);
hk=fft(h,L);
yk=x1k.*hk;
y2=ifft(yk);
y(k*N+1:(k+1)*N)=y2(4:10);
end
subplot(313),stem(n,y,'.');axis([0,30,0,600]);title('用重叠保留法求卷积');
12.2
nx=0:18;
x=3*nx+2;
h=[1,2,3,4];
M=length(h);
nh=0:M-1;
y1=conv(x,h);
n01=min(nx)+min(nh);
n02=max(nx)+max(nh);
ny1=[n01:n02];
subplot(321),stem(nx,x,'.');title('x(n)');
subplot(322),stem(nh,h,'.');title('h(n)');
subplot(312),stem(ny1,y1,'.');title('线性卷积');
N=7;
n=0:3*N-1;
x=[x,0,0];
ny=0:23;
y=zeros(1,length(ny));
for k=0:2
n1=k*N:(k+1)*N-1;
x1=x(find((n>=min(n1))&(n<=max(n1))));
xk=fft(x1,N+3);
hk=fft(h,N+3);
yk=xk.*hk;
y2=ifft(yk);
y2=abs(y2);
y(find(ny==min(n1)):find(ny==min(n1))+9)...
=y(find(ny==min(n1)):find(ny==min(n1))+9)+y2;
end
subplot(313),stem(ny,y,'.');title('用重叠相加法求卷积');
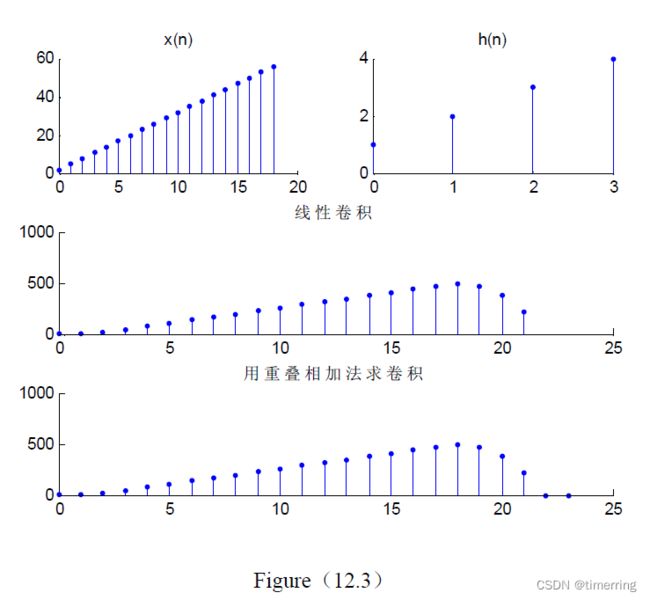
12.3
nx=0:18;
x=3*nx+2;
h=[1,2,3,4];
M=length(h);
nh=0:M-1;
y1=conv(x,h);
n01=min(nx)+min(nh);
n02=max(nx)+max(nh);
ny1=[n01:n02];
subplot(321),stem(nx,x,'.');title('x(n)');
subplot(322),stem(nh,h,'.');title('h(n)');
subplot(312),stem(ny1,y1,'.');title('线性卷积');
N=7;
n=0:3*N-1;
x=[x,0,0];
ny=0:23;
y=zeros(1,length(ny));
for k=0:2
n1=k*N:(k+1)*N-1;
x1=x(find((n>=min(n1))&(n<=max(n1))));
xk=fft(x1,N+3);
hk=fft(h,N+3);
yk=xk.*hk;
y2=ifft(yk);
y2=abs(y2);
y(find((ny>=min(n1))&(ny<=(max(n1)+3))))...
=y(find((ny>=min(n1))&(ny<=(max(n1)+3))))+y2;
end
subplot(313),stem(ny,y,'.');title('用重叠相加法求卷积');