python简单代码-手把手教你用Python创建简单的神经网络(附代码)
了解神经网络工作方式的***途径莫过于亲自创建一个神经网络,本文将演示如何做到这一点。
神经网络(NN)又称人工神经网络(ANN),是机器学习领域中基于生物神经网络概念的学习算法的一个子集。
拥有五年以上经验的德国机器学习专家Andrey Bulezyuk声称:"神经网络正在彻底改变机器学习,因为它们能够在广泛的学科和行业中为抽象对象高效建模。”
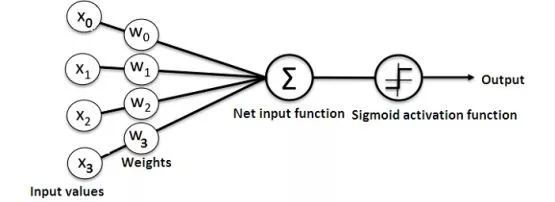
人工神经网络基本上由以下组件组成:
输入层:接收并传递数据
隐藏层
输出层
各层之间的权重
每个隐藏层都有一个激活函数。在这个简单的神经网络Python教程中,我们将使用Sigmoid激活函数。
神经网络有多种类型。在本项目中,我们将创建前馈或感知神经网络。这种类型的ANN直接将数据从前向后传递。
前馈神经元的训练往往需要反向传播,它为网络提供了相应的输入和输出集。当输入数据被传送到神经元时,经过处理后,产生一个输出。
下面的图表显示了一个简单的神经网络的结构:
了解神经网络如何工作的***方法是学习如何从头开始构建神经网络(而不是采用任何库)。
在本文中,我们将演示如何利用Python编程语言创建一个简单的神经网络。
问题
如下是一个展示问题的表格。
我们将提供一个新的数据集,利用它训练神经网络,从而能够预测正确的输出值。
正如上表所示,输出值总是等于输入部分中的***个值。因此,我们期望输出的值为1。
让我们看看是否可以使用Python代码来得出相同的结果(你可以在本文末尾仔细阅读这个项目的代码,然后再继续阅读本文)。
创建一个NeuralNetwork类
我们将用Python创建一个NeuralNetwork类来训练神经元,以期给出准确的预测。这个类还会有其他的帮助函数。
即使我们不会在这个简单的神经网络示例中使用神经网络库,我们也将导入numpy库来辅助计算。
numpy库提供了以下四种重要方法:
exp—用于生成自然指数
array—用于生成矩阵
dot—用于矩阵相乘
random—用于生成随机数。请注意,我们将生成随机数,以确保它们的有效分布。
1. 应用Sigmoid函数
我们将使用Sigmoid函数,来绘制一个特征"S”型曲线,作为神经网络的激活函数。
此函数可以将任何值映射到0到1之间的值,它将有助于我们对输入的加权和归一化。
此后,我们将创建Sigmoid函数的导数,以帮助计算权重的调整参数。
可以利用Sigmoid函数的输出来生成它的导数。例如,如果输出变量为"x”,则其导数为x*(1-x)。
2. 训练模型
这是我们教神经网络做出准确预测的阶段。每个输入都有一个权重-可为正值或负值。这意味着:有较大的正权重或负权重的输入会对结果的输出产生更大的影响。请记住,我们最初是通过为每个随机数分配一个权重后开始的。
下面是这个神经网络示例的训练过程:
***步:从训练数据集中提取输入,根据训练数据集的权重进行调整,并通过一种计算神经网络输出的方法对其进行筛选。
第二步:计算反向传播错误率。在这种情况下,它是神经元的预测输出与训练数据集的期望输出之间的差异。
第三步:利用误差加权导数公式,根据所得到的误差范围,进行了一些较小的权值调整。
第四步:对这一过程进行15000次迭代。在每次迭代中,整个训练集被同时处理。
我们使用".T”函数将矩阵从水平位置转换为垂直位置。因此,数字将以如下方式存储:
最终,神经元的权重将根据所提供的训练数据进行优化。随后,如果让神经元考虑一个新的状态,与先前的状态相同,它便可以作出一个准确的预测。这就是反向传播的方式。
打包运行
***,NeuralNetwork类初始化成功后,可以运行代码了。
下面是如何在Python项目中创建神经网络的完整代码:
import numpy as np
class NeuralNetwork():
def __init__(self):
# seeding for random number generation
np.random.seed(1)
#converting weights to a 3 by 1 matrix with values from -1 to 1 and mean of 0
self.synaptic_weights=2* np.random.random((3, 1)) - 1
def sigmoid(self, x):
#applying the sigmoid function
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(self, x):
#computing derivative to the Sigmoid function
return x * (1 - x)
def train(self, training_inputs, training_outputs, training_iterations):
#training the model to make accurate predictions while adjusting weights continually
for iteration in range(training_iterations):
#siphon the training data via the neuron
output=self.think(training_inputs)
#computing error rate for back-propagation
error=training_outputs- output
#performing weight adjustments
adjustments=np.dot(training_inputs.T, error * self.sigmoid_derivative(output))
self.synaptic_weights += adjustments
def think(self, inputs):
#passing the inputs via the neuron to get output
#converting values to floats
inputsinputs= inputs.astype(float)
output=self.sigmoid(np.dot(inputs, self.synaptic_weights))
return output
if __name__== "__main__":
#initializing the neuron class
neural_network=NeuralNetwork()
print("Beginning Randomly Generated Weights: ")
print(neural_network.synaptic_weights)
#training data consisting of 4 examples--3 input values and 1 output
training_inputs= np.array([[0,0,1],
[1,1,1],
[1,0,1],
[0,1,1]])
training_outputs=np.array([[0,1,1,0]]).T
#training taking place
neural_network.train(training_inputs, training_outputs, 15000)
print("Ending Weights After Training: ")
print(neural_network.synaptic_weights)
user_input_one=str(input("User Input One: "))
user_input_two=str(input("User Input Two: "))
user_input_three=str(input("User Input Three: "))
print("Considering New Situation: ", user_input_one, user_input_two, user_input_three)
print("New Output data: ")
print(neural_network.think(np.array([user_input_one, user_input_two, user_input_three])))
print("Wow, we did it!")
运行代码之后的输出:
这样,我们便成功地创建了一个简单的神经网络。
神经元首先给自己分配一些随机权重,接着,利用训练实例进行了自我训练。
之后,如果出现新的状态[1,0,0],则它得出的数值为0.9999584。
还记得我们想要的正确答案是1吗?
这个数值非常接近,Sigmoid函数输出值在0到1之间。
当然,在这个例子中,我们只使用一个神经元网络来完成简单的任务。如果我们把几千个人工神经网络连接在一起,情况将会是怎样呢?我们能不能完全模仿人类的思维方式呢?
【责任编辑:庞桂玉 TEL:(010)68476606】
点赞 0