运筹学修炼日记:TSP中两种不同消除子环路的方法及callback实现(Python调用Gurobi求解,附以王者荣耀视角解读callback的工作逻辑)
TSP中两种不同消除子环路的方法及callback实现
- 运筹学修炼日记:TSP中两种不同消除子环路的方法及callback实现(Python调用Gurobi求解)
- TSP问题的一般模型
-
- TSP Model 1: `subtour-elimination` 消除子环路
-
- TSP整数规划模型
- Python调用Gurobi实现中的一些小问题
- TSP Model 2 : MTZ约束消除子环路
-
- MTZ约束消除子环路
- 为什么`MTZ`约束可以消除子环路?
- Python+Gurobi: 用callback实现TSP的`subtour-elimination`
-
- `callback`的工作逻辑: 王者荣耀版独家解读
- 使用`callback`的通用步骤
- `callback`实现`subtour-elimination`的详细代码
- Python+Gurobi: 实现TSP的`MTZ`约束版
- 后记
- 参考文献
欢迎关注我们的微信公众号 运小筹
运筹学修炼日记:TSP中两种不同消除子环路的方法及callback实现(Python调用Gurobi求解)
TSP问题的一般模型
Traveling Salesman Problem(TSP),中文名叫旅行商问题,货郎担问题(前者更常见)。TSP的描述如下:
给定一系列的结点集合 V V V( ∣ V ∣ = N |V|=N ∣V∣=N),找到一条从该节点出发,依次不重复的经过所有其他节点,最终返回到出发点的最短路径。
如下图
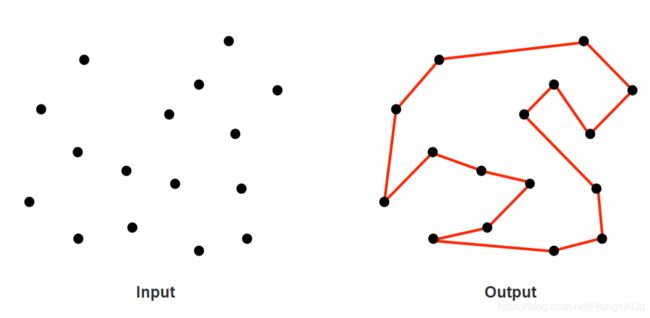
图片来自:http://algorist.com/problems/Traveling_Salesman_Problem.html
上述例子中的节点可以广义化成一系列的区域,如下图。但是本质是一样的问题。

图片来自http://www.math.uwaterloo.ca/tsp/methods/opt/subtour.htm
该问题是计算机领域和应用数学领域一个非常经典和重要的问题。下面我们来从运筹学的角度,来详细了解一下TSP。
直观上来讲,我们可以将问题建模为:
min ∑ i ∑ j c i j x i j ∑ i ∈ V x i j = 1, ∀ j ∈ V , i ≠ j ∑ j ∈ V x i j = 1, ∀ i ∈ V , i ≠ j x i j ∈ { 0, 1 } , ∀ i , j ∈ V \begin{aligned} \min\text{ }\sum_i{\sum_j{c_{ij}x_{ij}}} \\ \sum_{i\in V}{x_{ij}}=\text{1, } & \hspace{1cm}\forall j\in V,i\ne j \\ \sum_{j\in V}{x_{ij}}=\text{1, } & \hspace{1cm}\forall i\in V,i\ne j \\ x_{ij}\in \left\{ \text{0,}1 \right\} , & \hspace{1cm} \forall i,j\in V \end{aligned} min i∑j∑cijxiji∈V∑xij=1, j∈V∑xij=1, xij∈{0,1},∀j∈V,i=j∀i∈V,i=j∀i,j∈V
上面的模型:
- 约束1:每个点都被离开一次;
- 约束2:每个点都被到达一次。
也就是说,上面的两个约束联合起来,可以保证,获得的解一定满足:每一个点都被访问一次,并且,经过一个点就会离开一个点。看上去貌似是没错的吧,直觉上是可以得到一条上图中展示的路径的,依次不重复经过所有节点的封闭的完美路径。但是不然。
也就是说,上述模型并不正确,会导致一个叫做子环路subtour的东东出现。如下面的简单解释
子环路(subtour):没有包含所有节点的一条闭环。子环路首先是一个封闭的环;其次,这个环中被访问的节点集合(假设为 S S S)是所有节点集合 V V V的一个真子集,也就是 S ⊆ V S \subseteq V S⊆V。或者说 S ⊂ V , and ∣ V ∣ < N S \subset V, \,\text{and}\,\, |V| < N S⊂V,and∣V∣<N。如果上述模型的解出现了子环路,那么为了满足模型的约束1和约束2,解中必然至少存一个其他环路。这就导致与TSP想要得到的单环解矛盾,如下图所示的情况,图中出现了两个子环路。
图片来自http://www.math.uwaterloo.ca/tsp/methods/opt/subtour.htm
可以看到,子环路也完美的满足(i) 每个点只被访问一次,并且(ii) 经过一个点就离开那个点。但是这样的解会导致解中含有多个相离的环,也就是subtour。而我们需要的解是一个单个的经过所有点的大环。为了得到一个大环,我们就要添加消除子环路的约束,来完善TSP的模型。
这里比较常见的消除子环路的办法有两种:
- 加入
subtour-elimination约束 - 加入
Miller-Tucker-Zemlin(MTZ)约束
当然,之前我还钻研过TSP的另外一种建模思路,就是用1-tree的定义,结合纯图论的理论来支持建模的,日后我再专门写一个1-tree建模+column generation求解的文章。
TSP Model 1: subtour-elimination 消除子环路
TSP整数规划模型
之前,我们的问题描述中提到,图中点的个数为 N N N, ( ∣ V ∣ = N |V|=N ∣V∣=N)。subtour-elimination的思路比较直观,主要想法就是,根据子环路的特点,在模型中添加相应的约束,将其破开,用大白话说,就是破圈。
举个例子,假如考虑一个由图中点3个点 A , B , C A,B,C A,B,C组成的子点集, S = { A , B , C } S = \{A, B, C\} S={A,B,C}, 假定他们仨构成了一个环 A → B → C → A A \rightarrow B \rightarrow C \rightarrow A A→B→C→A。那么这个环出现,就导致问题的解就必须要满足:
x A B = x B C = x C A = 1 x_{AB}=x_{BC}=x_{CA}=1 xAB=xBC=xCA=1
换句话说,对于点 A , B , C A,B,C A,B,C组成的结点子集合 S = { A , B , C } S=\{A,B,C\} S={A,B,C}而言,必须要有
x A B + x B C + x C A ⩾ 3 x_{AB}+x_{BC}+x_{CA} \geqslant 3 xAB+xBC+xCA⩾3
也就是,只有上面这个条件成立,才会导致subtour的出现。
那么这个子环路不存在的条件就是(即破圈的方法)加入下面的约束
x A B + x B C + x C A < 3 x_{AB}+x_{BC}+x_{CA} < 3 xAB+xBC+xCA<3
也就是说,我们只允许所有点都被包含进来的环存在,即包含点的个数为N的环,删除其余所有的环。那怎么做呢,一个简单的想法就是枚举,也就是我们在TSP中经常看到的约束:
∑ i , j ∈ S x i j ⩽ ∣ S ∣ − 1, 2 ⩽ ∣ S ∣ ⩽ N − 1, S ⊂ V \begin{aligned} \sum_{i,j\in S}{x_{ij}}\leqslant \left| S \right|-\text{1, } & \hspace{0.5cm}2\leqslant \left| S \right|\leqslant N-\text{1,}S\subset V \end{aligned} i,j∈S∑xij⩽∣S∣−1, 2⩽∣S∣⩽N−1,S⊂V
可以看到 2 ⩽ ∣ S ∣ ⩽ N − 1, 2\leqslant \left| S \right|\leqslant N-\text{1,} 2⩽∣S∣⩽N−1,就是枚举了所有可能导致子环路出现的结点集合 V V V的集合(枚举个数的复杂度为 2 N 2^N 2N)。即我们只保留了 ∣ S ∣ = N \left| S \right| = N ∣S∣=N的环。因此,最终的TSP模型可以建模为下面的整数规划问题,该问题是一个经典的NP-hard问题。目前也没有特别好的精确算法。
min ∑ i ∑ j c i j x i j ∑ i ∈ V x i j = 1, ∀ j ∈ V , i ≠ j ∑ j ∈ V x i j = 1, ∀ i ∈ V , i ≠ j ∑ i , j ∈ S x i j ⩽ ∣ S ∣ − 1, 2 ⩽ ∣ S ∣ ⩽ n − 1, S ⊂ V x i j ∈ { 0, 1 } , ∀ i , j ∈ V \begin{aligned} \min\text{ }\sum_i{\sum_j{c_{ij}x_{ij}}} \\ \sum_{i\in V}{x_{ij}}=\text{1, } & \hspace{0.5cm}\forall j\in V,i\ne j \\ \sum_{j\in V}{x_{ij}}=\text{1, } & \hspace{0.5cm}\forall i\in V,i\ne j \\ \sum_{i,j\in S}{x_{ij}}\leqslant \left| S \right|-\text{1, } & \hspace{0.5cm}2\leqslant \left| S \right|\leqslant n-\text{1,}S\subset V \\ x_{ij}\in \left\{ \text{0,}1 \right\} , & \hspace{0.5cm} \forall i,j\in V \end{aligned} min i∑j∑cijxiji∈V∑xij=1, j∈V∑xij=1, i,j∈S∑xij⩽∣S∣−1, xij∈{0,1},∀j∈V,i=j∀i∈V,i=j2⩽∣S∣⩽n−1,S⊂V∀i,j∈V
【小坑1】 上面的模型中,是假设了网络是全连接的情况,也就是任何两个点都是可以直接到达的,这也是为什么前两条约束加了 i ≠ j i \ne j i=j的限制条件。不加这个条件,会使得解变成 x 11 = 1 , x 22 = 1 , ⋯ x_{11}=1,x_{22}=1, \cdots x11=1,x22=1,⋯你会发现它也满足约束。
这个小坑可是一定要注意一下,由于太小了,大佬们在论文中是不会拿出来说的,甚至在他们的模型中也没加上这个强调,因为他们觉得这都是常识,懒得跟你说,说了显得自己很没水平,哈哈。(我就不在意这个了,我本来就是个小菜。)很多人也没有明确的提出来这个问题。我在这里提一下,免得大家踩坑了又浪费很久去debug。
Python调用Gurobi实现中的一些小问题
这个subtour-elimination的约束,是一个枚举的约束,我们不能在建模的时候就直接全枚举,这样的话有 2 N 2^N 2N复杂度的情况。等到把这些约束枚举完,黄花菜都凉了。
啰嗦几句,
subtour-elimination的思路就是相当于cutting plane。在原来前两个约束的基础上,加上这个约束。但是如果你要在求解步骤model.optimize()之前就想全枚举,把subtour-elimination所有可能的 2 N 2^N 2N个约束全加上去,其他的不论,就只是加约束所耗费的时间,别人TSP早都解完去写Paper了,你这边约束还没加完。得不偿失,因此不能硬钢去枚举。
那怎么办呢?业内一般采用Gurobi或者CPLEX求解器中提供的callback(回调函数)的方法来动态的添加subtour-elimination约束。总的来讲,就是在branch and bound tree迭代的过程中,根据当前结点的松弛后的线性规划模型(relaxed LP)的解,来检查该解是否有存在子环路 subtour,如果有,我们就把执行subtour-elimination时候产生的破圈约束加到正在求解的模型中去; 如果没有,我们就直接接着迭代算法。
当然这个check的过程和branch and bound tree的过程是并行的。具体实现在下面展示。这里由于篇幅原因和为了保证可读性。我们先把这小节结束了。
TSP Model 2 : MTZ约束消除子环路
MTZ约束消除子环路
另外一种消除子环路的方法是加入Miller-Tucker-Zemlin(MTZ)约束。(本人认为这个方法的思想真的非常巧妙,做这个的时候就非常佩服前辈们的奇思妙想)。具体方法是:
对每个结点,引入一个决策变量μ i \mu _i μi- 利用 μ i \mu _i μi构造
Miller-Tucker-Zemlin(MTZ)约束
这样就可以完美的解决子环路的问题。
也就是引入决策变量 μ i , ∀ i ∈ V , μ i ⩾ 0 \mu _i, \forall i \in V, \mu _i\geqslant 0 μi,∀i∈V,μi⩾0,然后假如下面的MTZ约束
μ i − μ j + M x i j ⩽ M − 1, ∀ i , j ∈ V , i , j ≠ 0, i ≠ j \begin{aligned} \mu _i-\mu _j+Mx_{ij}\leqslant M-\text{1, } & \hspace{0.5cm}\forall i,j\in V,i,j\ne \text{0,}i\ne j \end{aligned} μi−μj+Mxij⩽M−1, ∀i,j∈V,i,j=0,i=j
【小思考1】 μ i \mu_i μi可以理解为点 i ∈ V i \in V i∈V的
访问次序。比如 μ 1 = 5 \mu_1=5 μ1=5,可以理解为点1是从出发点开始,第5个被访问到的点。很多最近的论文里也是这么解释的,再次验证了我的理解是和其他学者相近的。
【小思考2】 μ i \mu_i μi的取值范围一般设置成 μ i ⩾ 0 \mu _i\geqslant 0 μi⩾0,如果设置成无约束就会导致原问题不可行。
其中 M M M是一个很大的数,也是运筹学中非常常见的基本操作–逻辑约束(就是if ⋯ \cdots ⋯, then ⋯ \cdots ⋯)。参见课本[^3]
理论上来讲,根据课本中的说法, M M M应当是 μ i − μ j + 1 \mu_i - \mu_j +1 μi−μj+1的一个上界就可以,有论文指出,取最紧的上界,效果会好一些,因此我们取 M = N M=N M=N。参见文献[^4]。这样一来,上述约束可以拉紧为:
μ i − μ j + N x i j ⩽ N − 1, ∀ i , j ∈ V , i , j ≠ 0, i ≠ j \begin{aligned} \mu _i-\mu _j+Nx_{ij}\leqslant N-\text{1, } & \hspace{0.5cm}\forall i,j\in V,i,j\ne \text{0,}i\ne j \end{aligned} μi−μj+Nxij⩽N−1, ∀i,j∈V,i,j=0,i=j
我们还是整理成逻辑约束的形式吧,上面的看着费劲
μ i − μ j + 1 − N ( 1 − x i j ) ⩽ 0 ∀ i , j ∈ V , i , j ≠ 0, i ≠ j \begin{aligned} \mu _i-\mu _j+1-N\left( 1-x_{ij} \right) \leqslant \text{0 }\hspace{0.5cm}\forall i,j\in V,i,j\ne \text{0,}i\ne j \end{aligned} μi−μj+1−N(1−xij)⩽0 ∀i,j∈V,i,j=0,i=j
其中 N N N为节点的个数,也就是算例的大小。
这样,TSP问题的第二种最终版模型可以表示为
min ∑ i ∑ j c i j x i j ∑ i ∈ V x i j = 1, ∀ j ∈ V , i ≠ j ∑ j ∈ V x i j = 1, ∀ i ∈ V , i ≠ j μ i − μ j + N x i j ⩽ N − 1, ∀ i , j ∈ V , i , j ≠ 0, i ≠ j x i j ∈ { 0, 1 } , μ i ⩾ 0, μ i ∈ R 1 ∀ i ∈ V \begin{aligned} \min\text{ }\sum_i{\sum_j{c_{ij}x_{ij}}} \\ \sum_{i\in V}{x_{ij}}=\text{1, } & \hspace{1cm}\forall j\in V,i\ne j \\ \sum_{j\in V}{x_{ij}}=\text{1, } & \hspace{1cm}\forall i\in V,i\ne j \\ \mu _i-\mu _j+Nx_{ij}\leqslant N-\text{1, } & \hspace{1cm}\forall i,j\in V,i,j\ne \text{0,}i\ne j \\ x_{ij}\in \left\{ \text{0,}1 \right\} , \mu _i\geqslant \text{0, }\mu _i\in \mathbf{R}^1 &\hspace{1cm}\forall i\in V \end{aligned} min i∑j∑cijxiji∈V∑xij=1, j∈V∑xij=1, μi−μj+Nxij⩽N−1, xij∈{0,1},μi⩾0, μi∈R1∀j∈V,i=j∀i∈V,i=j∀i,j∈V,i,j=0,i=j∀i∈V
MTZ约束的加入,使得原问题增加了 N N N个连续变量和 N 2 N^2 N2复杂度个的逻辑约束,从代码实现上来讲,是非常方便的,比起subtour-elimination的实现要容易得多。
并且,就我看过的论文来讲,大家还是用MTZ约束多一些。像TRB,TRC,TRE, TS, EJOR上的文章,很多都是用MTZ约束,当然他们也不会在论文中指出这些约束是MTZ约束,他们只是说这是消除子环路的,毕竟MTZ也是常识了。具体论文我不在这里举例了,之后再找时间贴过来。
接下来还是列几个小坑在这里,把前面说过的坑也一并再强调一下。
【小坑2】
注意,实现这个的时候需要注意,由于μ \mu μ表示访问顺序,由于TSP的起点和终点是一致的,如果不做一些处理,就会出现infeasible的情况。为此,我们假如一个虚拟点,也就是将起始点s s scopy一份,作为终止点,其实他俩位置是一样的。这样的话,就不会存在问题了。
这个坑相信很多人都踩过,我在这里给还没踩过的小伙伴提个醒。
另外,就是实现的时候,一定记住,添加决策变量的时候,要判断i ≠ j i \ne j i=j,否则也会出问题。也就是x i j x_{ij} xij中, i ≠ j i \ne j i=j必须成立才能添加变量,否则肯定会出错。
我们将模型修正一下,变成点集为 V ′ = { 1 , 2 , ⋯ , N , N + 1 } V'=\{1,2,\cdots, N,N+1\} V′={1,2,⋯,N,N+1},一共 N + 1 N+1 N+1个点,其中点1和点 N + 1 N+1 N+1是同一个点,点1表示起点,点 N + 1 N+1 N+1表示终点。模型修正为
min ∑ i ∑ j c i j x i j ∑ i ∈ V x i j = 1, ∀ j ∈ { 2 , ⋯ N + 1 } , i ≠ j ∑ j ∈ V x i j = 1, ∀ i ∈ { 1 , ⋯ N } , i ≠ j μ i − μ j + N x i j ⩽ N − 1, ∀ i ∈ { 1 , ⋯ N } , j ∈ { 2 , ⋯ N + 1 } , i ≠ j x i j ∈ { 0, 1 } , μ i ⩾ 0, μ i ∈ R 1 ∀ i ∈ V \begin{aligned} \min\text{ }\sum_i{\sum_j{c_{ij}x_{ij}}} \\ \sum_{i\in V}{x_{ij}}=\text{1, } & \hspace{0.2cm}\forall j\in \{2,\cdots N+1\},i\ne j \\ \sum_{j\in V}{x_{ij}}=\text{1, } & \hspace{0.2cm}\forall i\in \{1,\cdots N\},i\ne j \\ \mu _i-\mu _j+Nx_{ij}\leqslant N-\text{1, } & \hspace{0.2cm}\forall i \in \{1,\cdots N\},j\in \{2,\cdots N+1\},i\ne j \\ x_{ij}\in \left\{ \text{0,}1 \right\} , \mu _i\geqslant \text{0, }\mu _i\in \mathbf{R}^1 &\hspace{0.2cm}\forall i\in V \end{aligned} min i∑j∑cijxiji∈V∑xij=1, j∈V∑xij=1, μi−μj+Nxij⩽N−1, xij∈{0,1},μi⩾0, μi∈R1∀j∈{2,⋯N+1},i=j∀i∈{1,⋯N},i=j∀i∈{1,⋯N},j∈{2,⋯N+1},i=j∀i∈V
请仔细琢磨上面约束1,约束2和约束3,不等式后面的comment部分的细微变化,这些都是为之后写代码的时候做基础,为了避免栽跟头。
接下来,我们解释一下为什么MTZ约束会work吧。
为什么MTZ约束可以消除子环路?
MTZ这个约束为什么能够消除子环路呢?
我们将MTZ约束、做一个变换,得到:
μ i − μ j + 1 + N ( x i j − 1 ) ⩽ 0 ∀ i ∈ { 1 , ⋯ n } , j ∈ { 2 , ⋯ N + 1 } , i ≠ j \begin{aligned} \mu _i-\mu _j+1+N\left( x_{ij}-1 \right) \leqslant \text{0 }\hspace{0.5cm} \forall i \in \{1,\cdots n\},j\in \{2,\cdots N+1\},i\ne j \end{aligned} μi−μj+1+N(xij−1)⩽0 ∀i∈{1,⋯n},j∈{2,⋯N+1},i=j
在上式中, ( x i j − 1 ) \left( x_{ij}-1 \right) (xij−1)并不是0-1变量,而 ( 1 − x i j ) \left( 1 - x_{ij} \right) (1−xij)才是0-1变量,因此该式变化成:
μ i − μ j + 1 − N ( 1 − x i j ) ⩽ 0 ∀ i ∈ { 1 , ⋯ n } , j ∈ { 2 , ⋯ N + 1 } , i ≠ j \begin{aligned} \mu _i-\mu _j+1-N\left( 1-x_{ij} \right) \leqslant \text{0 }\hspace{0.5cm} \forall i \in \{1,\cdots n\},j\in \{2,\cdots N+1\},i\ne j \end{aligned} μi−μj+1−N(1−xij)⩽0 ∀i∈{1,⋯n},j∈{2,⋯N+1},i=j
这个约束保证了,当 x i j = 1 x_{ij} = 1 xij=1时, μ i − μ j + 1 ⩽ 0 \mu_i - \mu_j + 1 \leqslant 0 μi−μj+1⩽0
我们任取 n , ( n ⩽ N ) n, (n\leqslant N) n,(n⩽N)个点,他们之间的被选择的总数小于等于 N − 1 N-1 N−1即是消除了子环路。举例来说,任取 i , j , k i, j, k i,j,k 3 个点,如果出现子环路,则有
x i j = x j k = x k i = 1 x i j + x j k + x k i = 3 \begin{aligned} x_{ij}=x_{jk}=x_{ki}&=1 \\ x_{ij}+x_{jk}+x_{ki}&=3 \end{aligned} xij=xjk=xkixij+xjk+xki=1=3
也就是说,根据MTZ约束,如果上述情况成立,则必有:
μ i − μ j + 1 ⩽ 0 μ j − μ k + 1 ⩽ 0 μ k − μ i + 1 ⩽ 0 \begin{aligned} \mu _i-\mu _j+1\leqslant 0 \\ \mu _j-\mu _k+1\leqslant 0 \\ \mu _k-\mu _i+1\leqslant 0 \end{aligned} μi−μj+1⩽0μj−μk+1⩽0μk−μi+1⩽0
将以上相加,我们得到
3 ⩽ 0 3\leqslant 0 3⩽0
上面不等式显然不成立,这说明,这个子环路不可能出现,这也就用反证法证明了,任一满足MTZ的点集,都不存在环路。而注意,我们的约束后的comment是 ∀ i ∈ { 1 , ⋯ N } , j ∈ { 2 , ⋯ N + 1 } , i ≠ j \forall i \in \{1,\cdots N\},j\in \{2,\cdots N+1\},i\ne j ∀i∈{1,⋯N},j∈{2,⋯N+1},i=j。这个在代码实现部分还是挺重要的。
其他情况,任意取 n n n个点,都是同样的道理。这个约束成功的避免了子环路。
下面我们来讲一下,Python调用Gurobi,如何用callback实现subtour-elimination,以及如何实现MTZ版的TSP求解吧。
Python+Gurobi: 用callback实现TSP的subtour-elimination
首先,我们还是以VRP上古大神solomon [^1]的benchmark为算例,来进行今天代码的数值实验部分。
算例下载地址:https://www.sintef.no/projectweb/top/vrptw/solomon-benchmark/100-customers/
在这之前,我想先说一下Gurobi和CPLEX里面的callback是怎么个逻辑:
callback的工作逻辑: 王者荣耀版独家解读
下面我夹杂王者荣耀的角度来轻松解释callback是怎么起作用的,打农药的小伙伴应该秒懂。(有些地方不严谨,但是大概是这么个意思,这段本来就是辅助理解,不严谨的地方可以私信我,我再修改)
1.之前说过,
subtour-elimination的想法,是想把所有的子集列举出来,为每一个子集添加破圈约束,但是这么做太慢。
2.于是我们想,先不加subtour-elimination的约束,我们先把只含有前两组约束的IP输入给Gurobi求解,Gurobi当然会先把IP的整数约束松弛掉,把模型变成LP,然后调用branch and bound算法,并将IP松弛后的relaxed LP作为根节点,进行branch and bound tree的迭代。
下面高能解释来了 我们把这个算法的迭代比作一场王者双排排位赛。假设我们准备开始玩游戏,我方打野选了野王Gurobi,OK,我见势立马一手奶妈蔡文姬,死跟打野,只干两件事1. 探视野(识别subtour)和2. 给助攻(根据subtour构建破圈约束)。Gurobi大佬构建模型,并且加入了前两组约束。(铭文带的不够呀,我有点慌,大佬却说,躺好看我carry, 帮我看蓝探视野),而我们也不示弱, 选了subtour-elimination的辅助装出装策略。(也就是subtour-elimination的callback函数,用于添加通过callback的方式添加subtour-elimination约束的)
3.游戏开始,Gurobi打着前两组约束,并且设置model.Params.lazyConstraints = 1也就是给我(软辅蔡文姬)发出跟着我的信号。然后拉着我一起双排开始了游戏,代码中就是model.optimize(subtourelim)。
OK,算法开始迭代。野王Gurobi还是基本操作,熟练的branch and bound在野区以最适合的刷野路径刷野。在刷野(迭代)的过程中,在每个branch and bound tree的结点处,Gurobi会去调用各种变式的simplex算法得到该节点的解。如果得到了一个整数解(也可以是得到小数解就操作),我们可以在这个地方,人为的插一脚,相当于Gurobi老哥正在屁颠屁颠刷野(跑算法)呢,我们在旁边探视野(做监工),一直就这么直勾的看着。我们看到老哥得到了一个整数解(或者一个小数可行解),一机灵,激动地过去拍拍Gurobi老哥的肩膀说,大佬,我拿一下这个节点的LP解哈,您继续。
4.OK, 拿到了LP的解以后,我们自己来看看这个解中存不存在subtour,如果我们检测完后发现不存在。尴尬,我们假装啥也没发生。继续静静地看着Gurobi老哥刷野(算法迭代)。下一次,Gurobi老哥又得到了一个整数解(或者一个小数可行解),我们再厚脸皮去拿过来检测,结果发现有2-5-8-2这个子环路混子混在里面,这次可被我逮个正着哈,小伙儿,你子环路了幺。我们激动地大声告诉Gurobi老哥:“老哥,老哥,子环路2-5-8-2在这儿挑衅你,你去GUNK它,把2-5-8-2这个混子送回家”,顺便我们还根据这个子环路2-5-8-2的特点,快速给Gurobi老哥想出了一套连招:老哥,你1433223就可以秒他!!!哈哈,在实际中,把这个子环路踢出去的方法(也就是刚刚的连招)就是加下面这个约束: x 25 + x 58 + x 82 ⩽ 2 x_{25}+x_{58}+x_{82} \leqslant 2 x25+x58+x82⩽2。这里还有个坑,虽然你也可以写成等价的 x 25 + x 58 + x 82 < 3 x_{25}+x_{58}+x_{82} < 3 x25+x58+x82<3,但是求解器是不接受 < < <, > > >这样的约束的,你要硬加,那就报错。很多人其实并不知道这一点,我在这里提一下。
5.接上面,Gurobi老哥非常强,手脚麻利动作快,脑子很好使能同时处理多个信息,听到了我们奶妈蔡文姬的报视野–前面草丛有个2-5-8-2的ADC很浪,落单了,还1433223连招可以秒他,回头敬个礼说:好嘞,知道了,放心吧,瞧好了您呐,看我把他怼出去哈。看这老哥如此稳的操作,我心中的默默点赞:同九义,何汝秀。然后继续监工。之后我就再也没见过2-5-8-2这个子环路混子。之后的监工中,我这奶妈蔡文姬又陆续把1-5-8-1,3-4-7-9-3等一众混子报给Gurobi老哥,老哥一一将他们1433223送回家。
6.由于我方打野位Gurobi老哥刚开始只加入了前两组约束,轻车简从,走路带风,身为奶妈蔡文姬的我紧跟打野,时刻监视打野行为,并不断为打野探视野,找敌方落单ADC,并每次都及时给个助攻subtour-elimination constraints( x 25 + x 58 + x 82 ⩽ 2 x_{25}+x_{58}+x_{82} \leqslant 2 x25+x58+x82⩽2),抢个人头,最终Gurobi老哥轻松carry全场,拿到2-5-8-2,3-4-7-9-3,1-5-8-1等3个人头 。直击敌方水晶,获得最优解[0, 4, 3, 7, 1, 2, 5, 8, 9, 6, 0]。评分127,夺得胜方MVP。起立,鼓掌!!!是的,每次都是这样。
上面的描述并不完美,但是我想,应该能给你一些辅助理解callback工作逻辑的帮助。
使用callback的通用步骤
其实总结一下,使用callback的方法分为下面几步(只针对本问题)
- 第一步:利用
Gurobi构建数学模型,只加入前两组约束; - 第二步:构建一个用来识别
subtour并返回消除子环路约束的函数subtourelim(model, where)(注意,这个函数的参数model,where是固定的,求解器规定的)。这个函数用于:拿到整数规划分支定界迭代过程中当前结点的解的信息,并根据当前节点的解,识别子环路,如有则返回消除子环路的约束,否则不作操作。 - 第三步:设置使用
lazyConstraints,并启动优化算法求解模型,也就是model.optimize(subtourelim),而且必须以callback函数subtourelim(model, where)为参数,具体代码为:
model._vars = X
model.Params.lazyConstraints = 1
model.optimize(subtourelim)
【Remark】这里,
subtourelim(model, where)中,添加子环路消除约束是以lazyConstraints的形式添加的,lazyConstraints就是不在建模一开始就加入,而是在算法迭代的过程中,动态的在branch and bound的分支节点处才加入的约束。可以通过callback函数,控制在节点的解满足什么样的条件下,我们去构建特定形式的约束,这个约束以lazyConstraints的形式构建并添加到求解的函数model.optimize()中,然后Gurobi就可以自动的识别,且调用callback函数,按照你的要求在求解过程中把约束加进去。这一招branch and cut,benders decomposition,row generation的时候用的非常多。想要进阶的小伙伴这招儿还是必须要攻克的。
callback实现subtour-elimination的详细代码
这部分代码有点长,待我明天再放出来把。算了,还是直接放上来把。
首先定义一些读取数据的函数:
readData(path, nodeNum):读取.txt文档中的算例数据;reportMIP(model, Routes):获得并打印最优解信息;getValue(var_dict, nodeNum):获得决策变量的值,并存储返回一个np.array()数组;getRoute(x_value):根据解x_value得到该解对应的路径。
# _*_coding:utf-8 _*_
'''
@author: Hsinglu Liu
@version: 1.0
@Date: 2019.5.5
'''
from __future__ import print_function
from __future__ import division, print_function
from gurobipy import *
import re;
import math;
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import copy
from matplotlib.lines import lineStyles
import time
starttime = time.time()
# function to read data from .txt files
def readData(path, nodeNum):
nodeNum = nodeNum;
cor_X = []
cor_Y = []
f = open(path, 'r');
lines = f.readlines();
count = 0;
# read the info
for line in lines:
count = count + 1;
if(count >= 10 and count <= 10 + nodeNum):
line = line[:-1]
str = re.split(r" +", line)
cor_X.append(float(str[2]))
cor_Y.append(float(str[3]))
# compute the distance matrix
disMatrix = [([0] * nodeNum) for p in range(nodeNum)]; # 初始化距离矩阵的维度,防止浅拷贝
# data.disMatrix = [[0] * nodeNum] * nodeNum]; 这个是浅拷贝,容易重复
for i in range(0, nodeNum):
for j in range(0, nodeNum):
temp = (cor_X[i] - cor_X[j])**2 + (cor_Y[i] - cor_Y[j])**2;
disMatrix[i][j] = (int)(math.sqrt(temp));
# disMatrix[i][j] = 0.1 * (int)(10 * math.sqrt(temp));
# if(i == j):
# data.disMatrix[i][j] = 0;
# print("%6.0f" % (math.sqrt(temp)), end = " ");
temp = 0;
return disMatrix;
def printData(disMatrix):
print("-------cost matrix-------\n");
for i in range(len(disMatrix)):
for j in range(len(disMatrix)):
#print("%d %d" % (i, j));
print("%6.1f" % (disMatrix[i][j]), end = " ");
# print(disMatrix[i][j], end = " ");
print();
def reportMIP(model, Routes):
if model.status == GRB.OPTIMAL:
print("Best MIP Solution: ", model.objVal, "\n")
var = model.getVars()
for i in range(model.numVars):
if(var[i].x > 0):
print(var[i].varName, " = ", var[i].x)
print("Optimal route:", Routes[i])
def getValue(var_dict, nodeNum):
x_value = np.zeros([nodeNum + 1, nodeNum + 1])
for key in var_dict.keys():
a = key[0]
b = key[1]
x_value[a][b] = var_dict[key].x
return x_value
def getRoute(x_value):
# 假如是5个点的算例,我们的路径会是1-4-2-3-5-6这样的,因为我们加入了一个虚拟点
# 也就是当路径长度为6的时候,我们就停止,这个长度和x_value的长度相同
x = copy.deepcopy(x_value)
# route_temp.append(0)
previousPoint = 0
arcs = []
route_temp = [previousPoint]
count = 0
while(len(route_temp) < len(x) and count < len(x)):
print('previousPoint: ', previousPoint, 'count: ', count)
if(x[previousPoint][count] > 0):
previousPoint = count
route_temp.append(previousPoint)
count = 0
continue
else:
count += 1
return route_temp
# cost = [[0, 7, 2, 1, 5],
# [7, 0, 3, 6, 8],
# [2, 3, 0, 4, 2],
# [1, 6, 4, 0, 9],
# [5, 8, 2, 9, 0]]
然后定义几个非常关键的用于添加subtour-elimination约束的函数:
subtourelim(model, where): callback函数,用于为model对象动态添加subtour-elimination约束;computeDegree(graph): 给定一个graph(二维数组形式),也就是给定一个邻接矩阵,计算出每个结点的degree.(degree=每个结点被进入次数+被离开的次数);findEdges(graph): 给定一个graph(二维数组形式),也就是给定一个邻接矩阵,找到该图中所有的边,例如[(1, 2), (2, 4), (2, 5)];subtour(graph):给定一个graph(二维数组形式),也就是给定一个邻接矩阵,找到该图中包含结点数目最少的子环路,例如[2, 3, 5]。
其中,函数subtourelim(model, where)中,调用了函数computeDegree(graph)、findEdges(graph)和subtour(graph)。
# Callback - use lazy constraints to eliminate sub-tours
# Callback - use lazy constraints to eliminate sub-tours
def subtourelim(model, where):
if(where == GRB.Callback.MIPSOL):
# make a list of edges selected in the solution
print('model._vars', model._vars)
# vals = model.cbGetSolution(model._vars)
x_value = np.zeros([nodeNum + 1, nodeNum + 1])
for m in model.getVars():
if(m.varName.startswith('x')):
# print(var[i].varName)
# print(var[i].varName.split('_'))
a = (int)(m.varName.split('_')[1])
b = (int)(m.varName.split('_')[2])
x_value[a][b] = model.cbGetSolution(m)
print("solution = ", x_value)
# print('key = ', model._vars.keys())
# selected = []
# for i in range(nodeNum):
# for j in range(nodeNum):
# if(i != j and x_value[i][j] > 0.5):
# selected.append((i, j))
# selected = tuplelist(selected)
# # selected = tuplelist((i,j) for i in range(nodeNum), for if x_value[i][j] > 0.5)
# print('selected = ', selected)
# find the shortest cycle in the selected edge list
tour = subtour(x_value)
print('tour = ', tour)
if(len(tour) < nodeNum + 1):
# add subtour elimination constraint for every pair of cities in tour
print("---add sub tour elimination constraint--")
# model.cbLazy(quicksum(model._vars[i][j]
# for i in tour
# for j in tour
# if i != j)
# <= len(tour)-1)
# LinExpr = quicksum(model._vars[i][j]
# for i in tour
# for j in tour
# if i != j)
for i,j in itertools.combinations(tour, 2):
print(i,j)
model.cbLazy(quicksum(model._vars[i, j]
for i,j in itertools.combinations(tour, 2))
<= len(tour)-1)
LinExpr = quicksum(model._vars[i, j]
for i,j in itertools.combinations(tour, 2))
print('LinExpr = ', LinExpr)
print('RHS = ', len(tour)-1)
# compute the degree of each node in given graph
def computeDegree(graph):
degree = np.zeros(len(graph))
for i in range(len(graph)):
for j in range(len(graph)):
if(graph[i][j] > 0.5):
degree[i] = degree[i] + 1
degree[j] = degree[j] + 1
print('degree', degree)
return degree
# given a graph, get the edges of this graph
def findEdges(graph):
edges = []
for i in range(1, len(graph)):
for j in range(1, len(graph)):
if(graph[i][j] > 0.5):
edges.append((i, j))
return edges
# Given a tuplelist of edges, find the shortest subtour
def subtour(graph):
# compute degree of each node
degree = computeDegree(graph)
unvisited = []
for i in range(1, len(degree)):
if(degree[i] >= 2):
unvisited.append(i)
cycle = range(0, nodeNum + 1) # initial length has 1 more city
edges = findEdges(graph)
edges = tuplelist(edges)
print(edges)
while unvisited: # true if list is non-empty
thiscycle = []
neighbors = unvisited
while neighbors: # true if neighbors is non-empty
current = neighbors[0]
thiscycle.append(current)
unvisited.remove(current)
neighbors = [j for i,j in edges.select(current,'*') if j in unvisited]
neighbors2 = [i for i,j in edges.select('*',current) if i in unvisited]
if(neighbors2):
neighbors.extend(neighbors2)
# print('current:', current, '\n neighbors', neighbors)
isLink = ((thiscycle[0], thiscycle[-1]) in edges) or ((thiscycle[-1], thiscycle[0]) in edges)
if(len(cycle) > len(thiscycle) and len(thiscycle) >= 3 and isLink):
# print('in = ', ((thiscycle[0], thiscycle[-1]) in edges) or ((thiscycle[-1], thiscycle[0]) in edges))
cycle = thiscycle
return cycle
return cycle
然后是建模部分的代码,建模部分相比学运筹的人比较熟悉,这里比较特殊的就是求解时候的几行代码:
model.Params.lazyConstraints = 1: set lazy constraints Parametermodel.optimize(subtourelim): use callback function when executing branch and bound algorithm
# nodeNum = 5
nodeNum = 10
# # path = 'C:\Users\hsingluLiu\eclipse-workspace\PythonCallGurobi_Applications\VRPTW\R101.txt';
path = 'solomon-100/in/c201.txt';
cost = readData(path, nodeNum)
printData(cost)
model = Model('TSP')
# creat decision variables
X = {}
mu = {}
for i in range(nodeNum + 1):
mu[i] = model.addVar(lb = 0.0
, ub = 100 #GRB.INFINITY
# , obj = distance_initial
, vtype = GRB.CONTINUOUS
, name = "mu_" + str(i)
)
for j in range(nodeNum + 1):
if(i != j):
X[i, j] = model.addVar(vtype = GRB.BINARY
, name = 'x_' + str(i) + '_' + str(j)
)
# set objective function
obj = LinExpr(0)
for key in X.keys():
i = key[0]
j = key[1]
if(i < nodeNum and j < nodeNum):
obj.addTerms(cost[key[0]][key[1]], X[key])
elif(i == nodeNum):
obj.addTerms(cost[0][key[1]], X[key])
elif(j == nodeNum):
obj.addTerms(cost[key[0]][0], X[key])
model.setObjective(obj, GRB.MINIMIZE)
# add constraints 1
for j in range(1, nodeNum + 1):
lhs = LinExpr(0)
for i in range(0, nodeNum):
if(i != j):
lhs.addTerms(1, X[i, j])
model.addConstr(lhs == 1, name = 'visit_' + str(j))
# add constraints 2
for i in range(0, nodeNum):
lhs = LinExpr(0)
for j in range(1, nodeNum + 1):
if(i != j):
lhs.addTerms(1, X[i, j])
model.addConstr(lhs == 1, name = 'visit_' + str(j))
# model.addConstr(X[0, nodeNum] == 0, name = 'visit_' + str(0) + ',' + str(nodeNum))
# set lazy constraints
model._vars = X
model.Params.lazyConstraints = 1
model.optimize(subtourelim)
# subProblem.optimize()
x_value = getValue(X, nodeNum)
# route = getRoute(x_value)
# print('optimal route:', route)
搞定。再重复一下,关键的地方就是subtourelim()这个函数和subtour(graph)这两个关键函数。还有就是求解的时候,别忘了model.optimize(subtourelim).就可以了。
Ok,我们将solomon100个点的VRP算例中的c201.txt拿出来,取钱10个点运行一下,结果为:
obj : 127
optimal route: [0, 4, 3, 7, 1, 2, 5, 8, 9, 6, 0]
完美!是不是觉得世界都又好了。哈哈,若干年前,我就是这种感觉。
Python+Gurobi: 实现TSP的MTZ约束版
首先定义一些读取数据的函数什么的,同上。
# _*_coding:utf-8 _*_
'''
@author: Hsinglu Liu
@version: 1.0
@Date: 2019.5.5
'''
# _*_coding:utf-8 _*_
'''
@author: Hsinglu Liu
@version: 1.0
@Date: 2019.5.5
'''
from __future__ import print_function
from __future__ import division, print_function
from gurobipy import *
import re;
import math;
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import copy
from matplotlib.lines import lineStyles
import time
starttime = time.time()
# function to read data from .txt files
def readData(path, nodeNum):
nodeNum = nodeNum;
cor_X = []
cor_Y = []
f = open(path, 'r');
lines = f.readlines();
count = 0;
# read the info
for line in lines:
count = count + 1;
if(count >= 10 and count <= 10 + nodeNum):
line = line[:-1]
str = re.split(r" +", line)
cor_X.append(float(str[2]))
cor_Y.append(float(str[3]))
# compute the distance matrix
disMatrix = [([0] * nodeNum) for p in range(nodeNum)]; # 初始化距离矩阵的维度,防止浅拷贝
# data.disMatrix = [[0] * nodeNum] * nodeNum]; 这个是浅拷贝,容易重复
for i in range(0, nodeNum):
for j in range(0, nodeNum):
temp = (cor_X[i] - cor_X[j])**2 + (cor_Y[i] - cor_Y[j])**2;
disMatrix[i][j] = (int)(math.sqrt(temp));
# disMatrix[i][j] = 0.1 * (int)(10 * math.sqrt(temp));
# if(i == j):
# data.disMatrix[i][j] = 0;
# print("%6.0f" % (math.sqrt(temp)), end = " ");
temp = 0;
return disMatrix;
def printData(disMatrix):
print("-------cost matrix-------\n");
for i in range(len(disMatrix)):
for j in range(len(disMatrix)):
#print("%d %d" % (i, j));
print("%6.1f" % (disMatrix[i][j]), end = " ");
# print(disMatrix[i][j], end = " ");
print();
def reportMIP(model, Routes):
if model.status == GRB.OPTIMAL:
print("Best MIP Solution: ", model.objVal, "\n")
var = model.getVars()
for i in range(model.numVars):
if(var[i].x > 0):
print(var[i].varName, " = ", var[i].x)
print("Optimal route:", Routes[i])
def getValue(var_dict, nodeNum):
x_value = np.zeros([nodeNum + 1, nodeNum + 1])
for key in var_dict.keys():
a = key[0]
b = key[1]
x_value[a][b] = var_dict[key].x
return x_value
def getRoute(x_value):
'''
input: x_value的矩阵
output:一条路径,[0, 4, 3, 7, 1, 2, 5, 8, 9, 6, 0],像这样
'''
# 假如是5个点的算例,我们的路径会是1-4-2-3-5-6这样的,因为我们加入了一个虚拟点
# 也就是当路径长度为6的时候,我们就停止,这个长度和x_value的长度相同
x = copy.deepcopy(x_value)
# route_temp.append(0)
previousPoint = 0
route_temp = [previousPoint]
count = 0
while(len(route_temp) < len(x)):
#print('previousPoint: ', previousPoint )
if(x[previousPoint][count] > 0):
previousPoint = count
route_temp.append(previousPoint)
count = 0
continue
else:
count += 1
return route_temp
'''
# toy example
cost = [[0, 7, 2, 1, 5],
[7, 0, 3, 6, 8],
[2, 3, 0, 4, 2],
[1, 6, 4, 0, 9],
[5, 8, 2, 9, 0]]
'''
然后就是Python调用Gurobi求解TSP的代码了(MTZ约束消除子环路)。MTZ的实现还是比较简单的。
# nodeNum = 5
nodeNum = 10
# # path = 'C:\Users\hsingluLiu\eclipse-workspace\PythonCallGurobi_Applications\VRPTW\R101.txt';
path = 'solomon-100/in/c201.txt';
cost = readData(path, nodeNum)
printData(cost)
model = Model('TSP')
# creat decision variables
X = {}
mu = {}
for i in range(nodeNum + 1):
mu[i] = model.addVar(lb = 0.0
, ub = 100 #GRB.INFINITY
# , obj = distance_initial
, vtype = GRB.CONTINUOUS
, name = "mu_" + str(i)
)
for j in range(nodeNum + 1):
if(i != j):
X[i, j] = model.addVar(vtype = GRB.BINARY
, name = 'x_' + str(i) + '_' + str(j)
)
# set objective function
obj = LinExpr(0)
for key in X.keys():
i = key[0]
j = key[1]
if(i < nodeNum and j < nodeNum):
obj.addTerms(cost[key[0]][key[1]], X[key])
elif(i == nodeNum):
obj.addTerms(cost[0][key[1]], X[key])
elif(j == nodeNum):
obj.addTerms(cost[key[0]][0], X[key])
model.setObjective(obj, GRB.MINIMIZE)
# add constraints 1
for j in range(1, nodeNum + 1):
lhs = LinExpr(0)
for i in range(0, nodeNum):
if(i != j):
lhs.addTerms(1, X[i, j])
model.addConstr(lhs == 1, name = 'visit_' + str(j))
# add constraints 2
for i in range(0, nodeNum):
lhs = LinExpr(0)
for j in range(1, nodeNum + 1):
if(i != j):
lhs.addTerms(1, X[i, j])
model.addConstr(lhs == 1, name = 'visit_' + str(j))
# add MTZ constraints
# for key in X.keys():
# org = key[0]
# des = key[1]
# if(org != 0 or des != 0):
# # pass
# model.addConstr(mu[org] - mu[des] + 100 * X[key] <= 100 - 1)
for i in range(0, nodeNum):
for j in range(1, nodeNum + 1):
if(i != j):
model.addConstr(mu[i] - mu[j] + 100 * X[i, j] <= 100 - 1)
model.write('model.lp')
model.optimize()
x_value = getValue(X, nodeNum)
route = getRoute(x_value)
print('optimal route:', route)
设置10个点跑一个toy example试试,结果为
Explored 683 nodes (4011 simplex iterations) in 0.19 seconds
Thread count was 8 (of 8 available processors)
Solution count 5: 127 137 150 ... 230
Optimal solution found (tolerance 1.00e-04)
Best objective 1.270000000000e+02, best bound 1.270000000000e+02, gap 0.0000%
optimal route: [0, 4, 3, 7, 1, 2, 5, 8, 9, 6, 10]
由于我们把起始点copy了一下,因此最优解为
obj : 127
optimal route: [0, 4, 3, 7, 1, 2, 5, 8, 9, 6, 0]
后记
运筹修炼真是个非常磨人的事情,需要理论与实战结合才能理解更深入。理论已经门槛够高了,再加上编程实现,可真要了命了。另外有非常多的小细节,大佬们在论文中并不会讲,但是又非常关键,只有自己实际一个一个去踩坑,或者多请教前辈,毕竟行万里路不如高人指路。
这里我把我的笔记和心得放在这里,供大家参考,互相交流学习,进步。也是为我自己整理、复习一下之前的知识。以后我自己复习的时候回来看也非常方便。
国内运筹学科普好文还是不太多见,很多都是从1到100的文章。分析讲述一些论文的idea什么的,都是为基础非常好的优秀者们看的。详细的讲述从0到1,如何把基础的东西吃透的文章比较少,让我们这些还不够强的孩子着实举步维艰,听讲座听得懂idea,但是做起来却啥啥也不行。真正搞运筹的,能将那些精确算法什么的都徒手复现的,就我所知,并不是很常见,大多数小伙伴似乎还是似懂非懂又不好意思多问(包括我)。希望以后有干货的,实用的文章越来越多,帮助众多学子解决基本的,底层的疑惑,而不是貌似人人都懂branch and cut, branch and price, branch and cut and price, benders, DW decomposition等等如何,但是似乎实现上又觉得捉襟见肘。看上去似乎国内OR人均水平为随手实现上述一系列精确算法如探囊取物。但是给我的感觉,似乎并不是。希望以后能够真正能够慢慢提高理论和实战水准,荷枪实弹学到真技术,为做有质量的学术打好基础。同时,也希望国内运筹发展越来越好吧。
参考文献
[1]: Desrochers, M., Desrosiers, J., & Solomon, M. (1992). A new optimization algorithm for the vehicle routing problem with time windows. Operations research, 40(2), 342-354. https://doi.org/10.1287/opre.40.2.342
[2]:Gurobi documents https://www.gurobi.com/documentation/
[3]:Winston, W. L., & Goldberg, J. B. (2004). Operations research: applications and algorithms (Vol. 3). Belmont^ eCalif Calif: Thomson/Brooks/Cole.
[4]:Desaulniers, G., Desrosiers, J., & Solomon, M. M. (Eds.). (2006). Column generation (Vol. 5). Springer Science & Business Media.
欢迎关注我们的微信公众号 运小筹
公众号往期推文如下





