列生成算法求解医疗救援方案（VS 2013 C++ , CPLEX）

序

在国内外疫情的大环境下，直播上课已经是第十周了。按学校规定，对《运筹学》课程安排了期中考试。在设计考试题目的时候，引用了《运筹学 原书第2版》Ronald L.Rardin.“Optimization in Operations Research”. 2nd Edition中书后练习题.13-2 （第十三章介绍的是大规模优化方法）

题目

医疗救助中心ERNow正在为小型直升机设计航班，这些小型直升机将用于向受到飓风影响的人们配送医疗、食品和住房物资。下表给出了不同物资重量占飞机可承载重量$w_i$的比列和容量占集装箱容量$v_i$的比例。

i	物资	重量$w_i$	容量$v_i$	需求量$q_i$
1	紧急救助补给	0.04	0.10	30
2	饮用水	0.20	0.14	20
3	柴油发电机	0.40	0.24	12
4	发电机燃油	0.28	0.32	23
5	帐篷	0.10	0.28	15
6	检测设备	0.16	0.24	30
7	毛毯	0.03	0.18	40
8	雨衣	0.08	0.14	25

ERNow希望用尽可能少的航班配送次数满足所有物资的需求。

模型建立

符号声明：
$x_j$ 表示装载组合$j$的运送次数；
$a_{ij}$ 表示在第$j$个装载组合中物资$i$的数量。
建立受限主问题模型（Restricted Master Problem, RMP）：

$\min z={\sum }_j{x}_j$

$s.t.$

${\sum }_j{a}_{ij}{x}_j\ge q_i,\forall i$

$x_j\ge 0,\forall j$

用${\pi }_i$表示物资$i$对应的对偶变量值，则可写出其列生成子问题模型（Sub-Problem, SP）：

$\min w=1-{\sum }_i{\pi }_i{y}_i$

$s.t.$

${\sum }_i{w}_i{y}_i\le 1$

${\sum }_i{v}_i{y}_i\le 1$

$y_i\ge 0,\forall i$

代码

在Microsoft Visual Studio 2013 C++编辑环境下，调用cplex 12.61，实现求解。

#include 
#include 
#include 
#include 
#include 

ILOSTLBEGIN

#define RC_EPS 1.0e-6

static void report1(IloCplex& RescueSolver, IloNumVarArray Rescue,
	IloRangeArray Require);
static void report2(IloAlgorithm& SchemeSolver,
	IloNumVarArray Supply,
	IloObjective obj);
static void report3(IloCplex& RescueSolver, IloNumVarArray Rescue);

void main()
{
	clock_t start_time = clock();
	IloEnv env;
	try{
		//Instance Data

		IloInt num = 8;
		IloNumArray weight(env, num, 0.04, 0.2, 0.4, 0.28, 0.1, 0.16, 0.03, 0.08),
			volume(env, num, 0.1, 0.14, 0.24, 0.32, 0.28, 0.24, 0.18, 0.14),
			demand(env, num, 30, 20, 12, 23, 15, 30, 40, 25);

		//Rescue-Optimization Problem 

		IloModel RescueOpt(env);
		IloObjective   CoptersUsed = IloAdd(RescueOpt, IloMinimize(env));
		IloRangeArray  Require = IloAdd(RescueOpt, IloRangeArray(env, demand, IloInfinity));
		IloNumVarArray Rescue(env);

		for (int j = 0; j < num; j++){
			Rescue.add(IloNumVar(CoptersUsed(1) + Require[j](min(int(1 / weight[j]), int(1 / volume[j])))));
		}

		IloCplex RescueSolver(RescueOpt);

		// Scheme-Generation Problem

		IloModel SchemeGen(env);
		
		IloObjective ReducedCost = IloAdd(SchemeGen, IloMinimize(env,1));
		IloNumVarArray Supply(env, num, 0, IloInfinity, ILOINT);
		SchemeGen.add(IloScalProd(weight, Supply) <= 1);
		SchemeGen.add(IloScalProd(volume, Supply) <= 1);

		IloCplex SchemeSolver(SchemeGen);

		// Column-Generation Procedure

		IloNumArray price(env, num);
		IloNumArray newScheme(env, num);

		for (;;){
			// Optimize over current schemes
			RescueSolver.solve();
			report1(RescueSolver, Rescue, Require);

			// Find and add a new scheme

			for (int i = 0; i < num; i++){
				price[i] = -RescueSolver.getDual(Require[i]);
			}
			ReducedCost.setLinearCoefs(Supply, price);

			SchemeSolver.solve();
			report2(SchemeSolver, Supply, ReducedCost);

			if (SchemeSolver.getValue(ReducedCost)>-RC_EPS) break;

			SchemeSolver.getValues(newScheme, Supply);
			Rescue.add(IloNumVar(CoptersUsed(1) + Require(newScheme)));
		}
		
		RescueOpt.add(IloConversion(env, Rescue, ILOINT));
		RescueSolver.solve();
		cout << "Solution status: " << RescueSolver.getStatus() << endl;
		report3(RescueSolver, Rescue);
	}
	catch (IloException& ex) {
		cerr << "Error: " << ex << endl;
	}
	catch (...) {
		cerr << "Error" << endl;
	}

	env.end();
	clock_t finish_time = clock();
	cout << "Computing time: " << (finish_time - start_time) / 1000 << "seconds" << endl;
	system("pause");
}


static void report1(IloCplex& RescueSolver, IloNumVarArray Rescue,
	IloRangeArray Require)
{
	cout << endl;
	cout << "Using " << RescueSolver.getObjValue() << " copters" << endl;
	cout << endl;
	for (IloInt j = 0; j < Rescue.getSize(); j++) {
		cout << "  Rescue" << j << " = " << RescueSolver.getValue(Rescue[j]) << endl;
	}
	cout << endl;
	for (IloInt i = 0; i < Require.getSize(); i++) {
		cout << "  Require" << i << " = " << RescueSolver.getDual(Require[i]) << endl;
	}
	cout << endl;
}

static void report2(IloAlgorithm& SchemeSolver, IloNumVarArray Supply,
	IloObjective obj)
{
	cout << endl;
	cout << "Reduced cost is " << SchemeSolver.getValue(obj) << endl;
	cout << endl;
	if (SchemeSolver.getValue(obj) <= -RC_EPS) {
		for (IloInt i = 0; i < Supply.getSize(); i++)  {
			cout << "  Supply" << i << " = " << SchemeSolver.getValue(Supply[i]) << endl;
		}
		cout << endl;
	}
}

static void report3(IloCplex& RescueSolver, IloNumVarArray Rescue)
{
	cout << endl;
	cout << "Best integer solution uses "
		<< RescueSolver.getObjValue() << " copters" << endl;
	cout << endl;
	for (IloInt j = 0; j < Rescue.getSize(); j++) {
		cout << "  Rescue" << j << " = " << RescueSolver.getValue(Rescue[j]) << endl;
	}
}

运行结果

列生成算法-初始方案

此时主问题最优目标值为44.7381，即需要使用44.7381架次直升机运输物资：

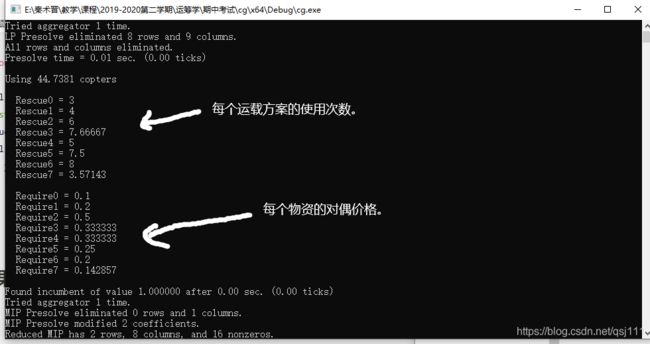
其中初始方案（Rescue i, i=0,…,7）分别为只满载运送第i+1种物资的情况。

Rescue2 = 6 表示
最优解中 只满载运送第3种物资的运输方案 使用了6次。

列生成算法-第一次迭代

此时主问题最优目标值为41.480952，即需要使用41.480952架次直升机运输物资：

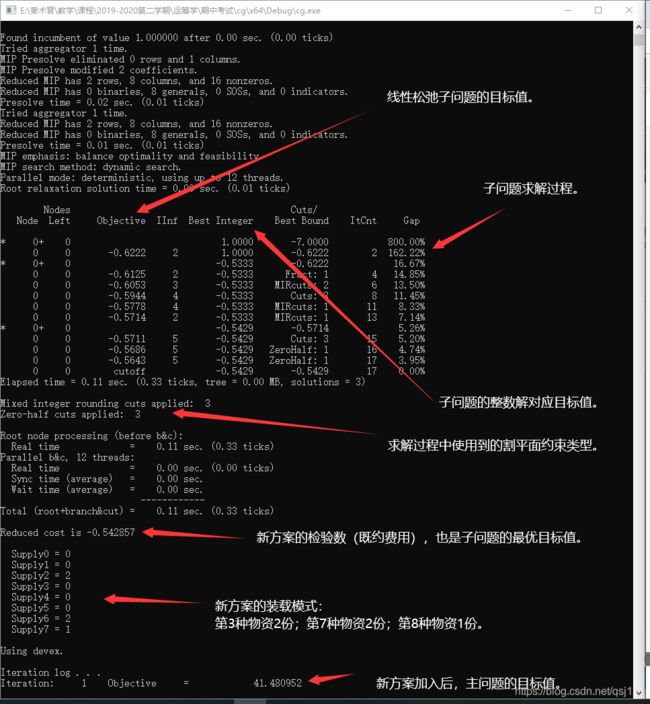
列生成算法-第2次迭代

此时主问题最优目标值为40.1，即需要使用40.1架次直升机运输物资：

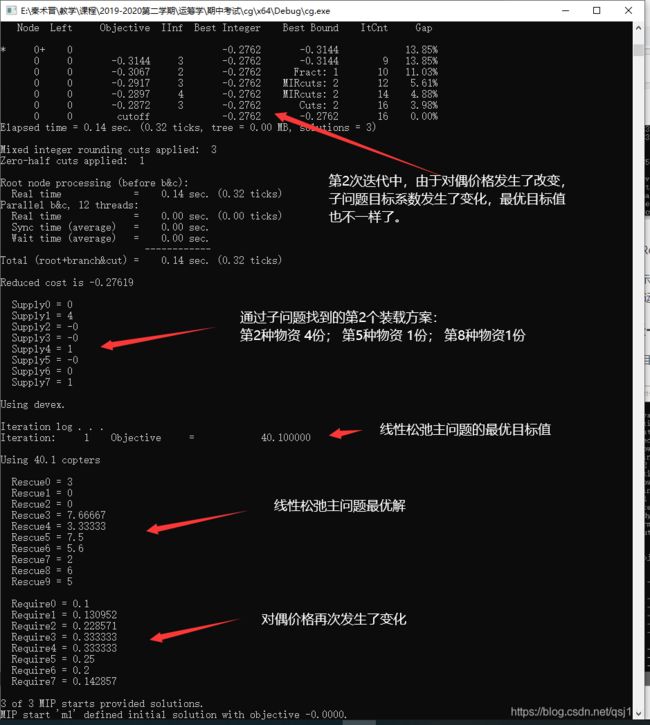
列生成算法-第13次迭代

此时主问题最优目标值为38.14，即需要使用38.14架次直升机运输物资：

列生成算法-第14次迭代

子问题已经找不到检验数小于0的装载方案，迭代终止。

列生成算法-取整

这里就简单对已找到的方案寻找最优组合。整个列生成算法的总用时为2秒。

列生成算法-装载方案详情及每阶段目标值

装载方案编号	1	2	3	4	5	6	7	8	线性松弛主问题目标值
0	10	0	0	0	0	0	0	0	-
1	0	5	0	0	0	0	0	0	-
2	0	0	2	0	0	0	0	0	-
3	0	0	0	3	0	0	0	0	-
4	0	0	0	0	3	0	0	0	-
5	0	0	0	0	0	4	0	0	-
6	0	0	0	0	0	0	5	0	-
7	0	0	0	0	0	0	0	7	44.7381
8	0	0	2	0	0	0	2	1	41.480952
9	0	4	0	0	1	0	0	1	40.100000
10	0	0	0	0	3	0	0	1	39.623810
11	1	0	0	0	0	0	5	0	39.063810
12	0	2	0	0	0	3	0	0	38.706667
13	0	0	0	0	0	2	0	2	38.706667
14	0	0	0	2	0	0	2	0	38.400000
15	2	0	2	0	0	0	1	1	38.280000
16	3	3	0	0	1	0	0	0	38.205000
17	2	0	0	0	2	1	0	0	38.204762
18	0	0	0	0	1	0	3	0	38.178571
19	2	0	1	0	2	0	0	0	38.175497
20	2	0	1	0	0	0	0	3	38.140000