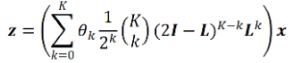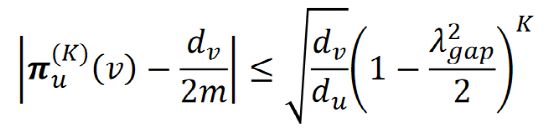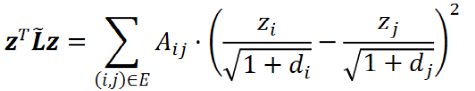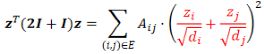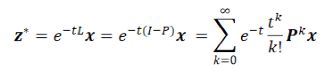人大魏哲巍:图神经网络的理论基础
【专栏:研究思路】近年来,由于图结构数据的强大表现力,用机器学习方法分析图的研究越来越受到重视。图神经网络是一类基于深度学习的处理图结构数据的方法,在众多领域展现出了卓越的性能,因此已成为一种广泛应用的图分析方法。
中国人民大学魏哲巍教授从当前流行的图神经网络模型出发,分别从图信号滤波器、随机游走和优化函数三个视角探讨图神经网络的理论基础,并介绍在这三个方面所做的一些工作,最后讨论图神经网络研究的一些挑战和对未来工作的展望。
魏哲巍教授从上述三个视角对图神经网络展开分析,并指出它们分别对应图的谱域解释、空域解释、深度展开。本文将会对图谱、图的傅里叶变换、图卷积等概念进行介绍,帮助读者梳理图神经网络研究的理论基础。
本文整理自青源Talk第七期,视频回放链接:https://event.baai.ac.cn/activities/179
此外,魏哲巍教授对青年学生的寄语如下:
魏哲巍,中国人民大学教授,博导。2008年本科毕业于北京大学数学科学学院,2012年博士毕业于香港科技大学计算机系;2012年至2014年于奥胡斯大学海量数据算法研究中心担任博士后研究员,2014年9月加入中国人民大学信息学院担任副教授,2019年8月起任教授。2020年4月加入高瓴人工智能学院。在数据库、理论计算机、数据挖掘、机器学习等领域的顶级会议及期刊上(如SIGMOD、VLDB、ICML、NeurIPS、KDD、SODA等)发表论文50余篇。担任PODS、ICDT等大数据理论会议论文集主席以及VLDB、KDD、ICDE、ICML、NeurIPS等国际会议程序委员会委员。主持多项自然科学基金青年项目、面上项目及重点项目子课题。担任人工智能与数字经济广东省实验室(广州)(简称琶洲实验室)青年科学家。
演讲:魏哲巍
整理:熊宇轩
审校:李梦佳
01
图的基本定义
在现实生活中,图数据无处不在。例如,在社交网络中,可以将用户作为节点,好友关系、转发关系、点赞关系作为图中的边;在论文引用网络中,论文为节点,引用关系为边;在通讯信号网络中,信号基站、手机为节点,边的权重为节点之间的信号强度。
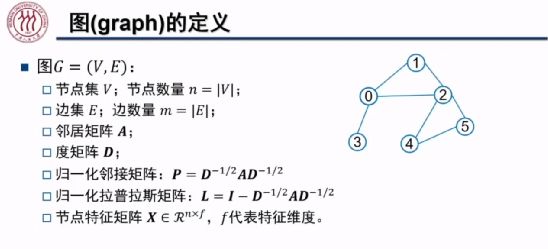
在无向图![]() 中,我们将节点集合定义为 V,其节点个数为 n;边集为 E,其节点个数为 m。若节点 i 和节点 j 之间存在连接关系(边),则邻接矩阵 A 中对应的元素
中,我们将节点集合定义为 V,其节点个数为 n;边集为 E,其节点个数为 m。若节点 i 和节点 j 之间存在连接关系(边),则邻接矩阵 A 中对应的元素![]() 值为 1,否则该元素的值为 0, A 为一个对称矩阵。ji矩阵 D 为一个对角矩阵,第 i 行对角线上的元素
值为 1,否则该元素的值为 0, A 为一个对称矩阵。ji矩阵 D 为一个对角矩阵,第 i 行对角线上的元素![]() 为节点 i 的邻居节点的数量。归一化后的邻接矩阵 P 为邻接矩阵 A 分别左乘、右乘
为节点 i 的邻居节点的数量。归一化后的邻接矩阵 P 为邻接矩阵 A 分别左乘、右乘![]() ,其中对角矩阵
,其中对角矩阵![]() 对角线上的元素为度矩阵 D 对角线上每个对应元素开根号、取倒数后的结果。归一化后的拉普拉斯矩阵为单位矩阵 I 与归一化后的邻接矩阵 P 之差。
对角线上的元素为度矩阵 D 对角线上每个对应元素开根号、取倒数后的结果。归一化后的拉普拉斯矩阵为单位矩阵 I 与归一化后的邻接矩阵 P 之差。
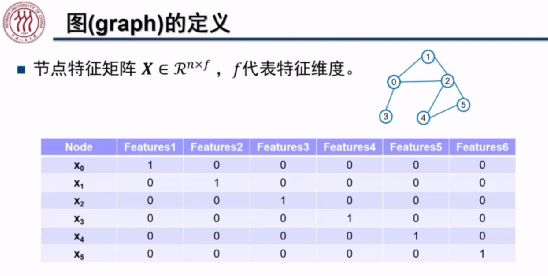
除了刻画图结构信息的矩阵之外,我们将刻画每个节点特征信息的矩阵记为![]() ,其中 n 为节点个数,f 为特征维度。例如,上图中六个节点的特征分别为一个维数为六的 one-hot 向量。
,其中 n 为节点个数,f 为特征维度。例如,上图中六个节点的特征分别为一个维数为六的 one-hot 向量。
02
图神经网络概述
图卷积神经网络(GCN)
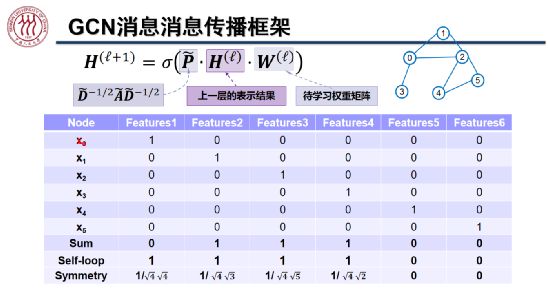
Kipf 等人于 ICLR 2017 提出了 GCN,希望在图结构上聚合邻域信息,学习消息传递过程中的权重。如上图所示,在计算第 l+1 层表示的公式中,![]() 为第 l 层的表示结果,
为第 l 层的表示结果,![]() 为每个节点带有自环的正则化之后的邻接矩阵,
为每个节点带有自环的正则化之后的邻接矩阵,![]() 为待学习的权重矩阵,
为待学习的权重矩阵,![]() 为非线性激活函数。上图中从上往下数最后三行为计算节点 0 表示的过程。
为非线性激活函数。上图中从上往下数最后三行为计算节点 0 表示的过程。
我们可以将卷积神经网络(CNN)看做一种特殊的图卷积神经网络(GCN)。当我们使用 3*3 的卷积核提取图像信息时,将中心节点![]() 周围的八个邻居节点及其自身的信息聚合起来,得到了新的表征。值得注意的是,在 CNN 中,每个节点与中心节点在信息聚合时的权值 w 是可以通过学习得到的,而 GCN 中节点之间的聚合权值仅由每个节点的度决定。
周围的八个邻居节点及其自身的信息聚合起来,得到了新的表征。值得注意的是,在 CNN 中,每个节点与中心节点在信息聚合时的权值 w 是可以通过学习得到的,而 GCN 中节点之间的聚合权值仅由每个节点的度决定。
图神经网络已经被应用于节点分类、链接预测、社区发现等任务。例如在交通领域,DeepMind 利用图神经网络预测各个道路节点之间的交通流量,改进了 Google Map 的出行时间预测功能。在药物研发领域,研究者们将原子看做分子图中的节点,将化学键视为分子图中的边,利用图神经网络提取分子特征,预测分子的属性,从而筛选出制药所需要的合理分子结构。KDD Cup 2021 设立了大规模分子性质预测竞赛。
网址:Https://ogb.stanford.edu/kddcup2021
03
图神经网络的三个视角
滤波器:GNN 的谱域解释
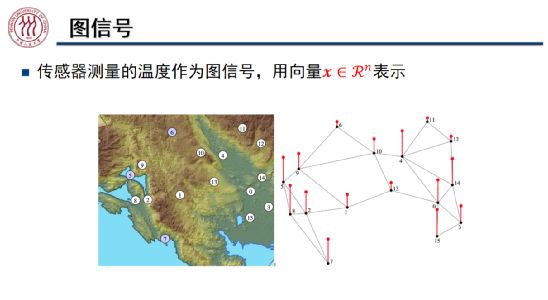
我们可以用向量表示图上的信号。如上图所示,我们将地图上不同的观测点作为图中的节点,节点上的红色线段的高度代表该观测点测量到的温度,这里测量到的温度可能不准确,带有一定的噪声。从图信号处理的角度出发,我们希望通过该观测点周围的信号对其进行平滑处理,使得该观测点的温度数据更加准确。具体而言,我们将图中节点的信号与拉普拉斯矩阵 L 的函数相乘,从而将节点的信号向邻居节点传播。
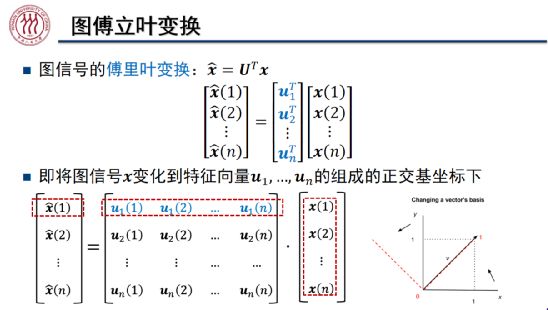
我们根据拉普拉斯矩阵的特征分解将图的傅里叶变换定义为如上图所示的形式。如前文所述,拉普拉斯矩阵 L 是一个对称矩阵,我们可以将其分解为三个矩阵的乘积。其中![]() 为对角矩阵,对角线上的值为特征值,特征值的取值范围为 [0,2]。
为对角矩阵,对角线上的值为特征值,特征值的取值范围为 [0,2]。![]() 和
和![]() 为正交矩阵,
为正交矩阵,![]() 的每一个分量为拉普拉斯矩阵 L 的特征向量,其二范数为 1。由于 L 为对称矩阵,所以
的每一个分量为拉普拉斯矩阵 L 的特征向量,其二范数为 1。由于 L 为对称矩阵,所以![]() 的任意两个特征向量正交,即点积为零。由于
的任意两个特征向量正交,即点积为零。由于![]() 和
和![]() 为正交矩阵,则二者乘积为单位矩阵,因此图信号的傅里叶变换和傅里叶逆变换的关系成立。
为正交矩阵,则二者乘积为单位矩阵,因此图信号的傅里叶变换和傅里叶逆变换的关系成立。
如上图所示,图信号的傅里叶变换令图上的信号左乘![]() ,相当于对笛卡尔坐标系下的图信号
,相当于对笛卡尔坐标系下的图信号![]() 旋转,将其变换到由
旋转,将其变换到由![]() 中特征向量组成的正交基坐标下。
中特征向量组成的正交基坐标下。
如上图所示,传统的时域-频域上的傅里叶变换是将时域中的函数分解为不同频率的波动函数的线性组合,此时我们可以将不同频率的信号看做一组正交基。就图傅里叶变换而言,我们可以将负无穷与正无穷相连的实数轴刻画为环状图,其特征向量的频率随着特征值的增加而增加,因此小的特征值对应低频特征向量,而大的特征值对应高频特征向量。可见,图傅里叶变换是将一组空域上的图信号转换为一组波动频率逐渐升高的正交基下的坐标的变换。
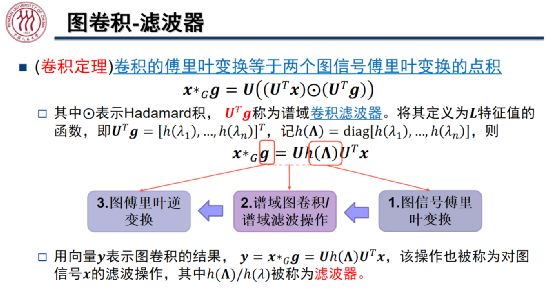
在对图信号![]() 进行滤波的过程中,我们首先对图信号进行傅里叶变换,接着我们对频谱域中的特征值做滤波操作,过滤掉某些频率的信息,进而将滤波后的信号通过图傅里叶逆变换转换到原始空间中。其中,
进行滤波的过程中,我们首先对图信号进行傅里叶变换,接着我们对频谱域中的特征值做滤波操作,过滤掉某些频率的信息,进而将滤波后的信号通过图傅里叶逆变换转换到原始空间中。其中,![]() /
/![]() 为滤波器,当
为滤波器,当![]() 都等于 1 时,该滤波器相当于一个全通滤波器。
都等于 1 时,该滤波器相当于一个全通滤波器。
卷积定理指出,卷积的傅里叶变换等于两个信号傅里叶变换的点积(Hadamard 积)。![]() 为谱域的卷积滤波器,它是 L 特征值的函数。如上图所示,图上的卷操作可以写作图傅里叶变换的形式。
为谱域的卷积滤波器,它是 L 特征值的函数。如上图所示,图上的卷操作可以写作图傅里叶变换的形式。
在节点分类任务中,滤波器起到了决定性的作用。我们将边相连的节点通常属于同一类的图称为同配图,将边相连的节点通常属于不同类的图称为异配图。低通滤波器适用于同配图的分类,高通滤波器适用于对异配图的分类。
不幸的是,处于计算开销的考量,当节点数较多时,稠密矩阵![]() 的规模过大,特征值分解的复杂度太高。为此,目前主流的图卷积神经网络算法采用多项式近似滤波器,从而降低计算复杂度。
的规模过大,特征值分解的复杂度太高。为此,目前主流的图卷积神经网络算法采用多项式近似滤波器,从而降低计算复杂度。
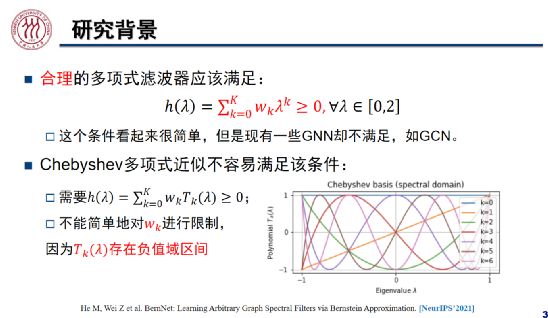
在 ChebNet 中,作者采用切比雪夫多项式近似滤波器,其表示能力强于 GCN。如上图所示,不同颜色的曲线代表了不同阶切比雪夫多项式对应的基,随着多项式阶数上升,其频率越来越高,这与图傅里叶变换类似。
ChebNet 在一些半监督任务上的效果欠佳。为此,Kipf 等人于 2017 年提出 GCN,简化了 ChebNet,只使用了前两阶的切比雪夫多项式,并且通过加入自环进行了重归一化。然而,该模型在进行节点分类时,只能使用两层 GCN,即利用 2 以内的邻居信息。
![]()
以低通滤波器为例,单层 GCN 低通滤波器可以线性地保留低频信号,过滤高频信号。但是,随着 GCN 层数 K 上升,滤波器会越来越平滑,在 K 极大的情况下几乎只允许最低频的信号通过。
此外,研究者们尝试使用各种各样的多项式学习滤波器。以 ICLR 2021 上发表的论文 GPR-GNN 为例,作者利用了 Monomial 学习多项式系数![]() 。
。![]() 大于等于零时,该网络相当于低通滤波器;
大于等于零时,该网络相当于低通滤波器;![]() 时,该网络相当于高通滤波器。然而,该架构缺乏可解释性,不能解释学到的任意滤波器。
时,该网络相当于高通滤波器。然而,该架构缺乏可解释性,不能解释学到的任意滤波器。
BernNet: Learning Arbitrary Graph Spectral Filters via Bernstein Approximation(NeurIPS, 2021)
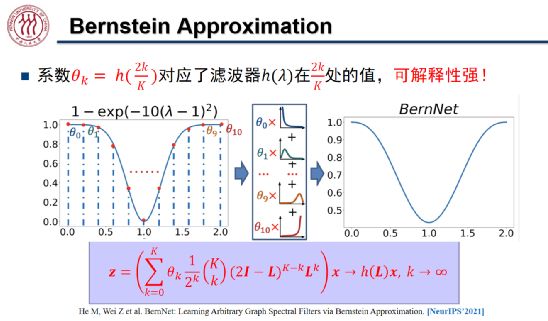
在 NeurIPS 2021 上,魏哲巍教授团队提出了 BernNet,该架构可以学习/设计任意的谱滤波器。如前文所述,特征值![]() ,合理的多项式滤波器
,合理的多项式滤波器![]() 。若
。若![]() 小于零,图神经网络的滤波结果会随着层数的奇偶变化震荡。然而,GCN 等图神经网络并不满足上述条件。
小于零,图神经网络的滤波结果会随着层数的奇偶变化震荡。然而,GCN 等图神经网络并不满足上述条件。
魏哲巍教授团队发现,在谱域上,![]() 区间内非负的任意多项式可以写成 Bernstein 多项式的形式,该多项式的系数
区间内非负的任意多项式可以写成 Bernstein 多项式的形式,该多项式的系数![]() ,我们可以用一组 Bernstein 基线性近似任意多项式,从而学习任意的滤波器。受此启发,我们将 BernNet 模型定义为:
,我们可以用一组 Bernstein 基线性近似任意多项式,从而学习任意的滤波器。受此启发,我们将 BernNet 模型定义为:
Bernstein 多项式为 BernNet 带来了很强的可解释性,其中![]() 对应滤波器
对应滤波器![]() 在
在![]() 处的函数值。如上图所示,假设滤波器函数为拒绝中频信号的
处的函数值。如上图所示,假设滤波器函数为拒绝中频信号的![]() ,我们将[0,2]均匀分成 k 分,将「0」、「2」及每个分位数对应的
,我们将[0,2]均匀分成 k 分,将「0」、「2」及每个分位数对应的![]() 定义为系数
定义为系数![]() 。我们将这组系数与对应的伯恩斯坦多项式线性组合起来就得到了右侧 BernNet 的曲线。为了保证
。我们将这组系数与对应的伯恩斯坦多项式线性组合起来就得到了右侧 BernNet 的曲线。为了保证![]() ,我们只需将
,我们只需将![]() 重参数化为
重参数化为![]() ,从而保证该滤波器的值恒大于等于零。这样一来,我们就可以学习任意的滤波器,且拟合精度随着 k 的增加而提升。
,从而保证该滤波器的值恒大于等于零。这样一来,我们就可以学习任意的滤波器,且拟合精度随着 k 的增加而提升。
随机游走:GNN 的空域解释
在随机游走的马尔科夫过程中,我们在每一步上从某节点以相等的概率走向该节点的某个相邻节点,概率转移矩阵记为![]() 。大部分随机游走过程会收敛到某个稳态上,即
。大部分随机游走过程会收敛到某个稳态上,即![]() 。在无向图上,节点 v 处的稳态为
。在无向图上,节点 v 处的稳态为![]() ,即 v 点的度除以两倍的图中边总数。可见,稳态分布与随机游走的起始节点无关。我们可以通过 Cheeger 不等式刻画在随机游走中收敛的速度,该不等式也可以被用于社区发现:
,即 v 点的度除以两倍的图中边总数。可见,稳态分布与随机游走的起始节点无关。我们可以通过 Cheeger 不等式刻画在随机游走中收敛的速度,该不等式也可以被用于社区发现:
其中![]() 为从节点 u 开始的第 K 步随机游走,
为从节点 u 开始的第 K 步随机游走,![]() 为拉普拉斯矩阵最小的非零特征值。
为拉普拉斯矩阵最小的非零特征值。
我们可以通过随机游走解释 GCN 的过平滑现象。如上图所示,在去掉激活函数后,第 K 层的图表示结果为![]() ,将归一化后的邻接矩阵展开后,可得
,将归一化后的邻接矩阵展开后,可得![]() 。其中
。其中![]() 为 K 步随机游走后的概率分布,随着 K 的增大会收敛到稳态。也就是说,最终的图表示只与图的结构相关,与随机游走初始节点无关。随着图卷积网络层数加深,网络会逐渐「忘记」初始特征,出现过平滑现象,导致节点分类效果较差。
为 K 步随机游走后的概率分布,随着 K 的增大会收敛到稳态。也就是说,最终的图表示只与图的结构相关,与随机游走初始节点无关。随着图卷积网络层数加深,网络会逐渐「忘记」初始特征,出现过平滑现象,导致节点分类效果较差。
一些研究者曾试图通过加入残差连接(自环)解决过平滑,但该操作并不能奏效,因为该情况下的随机游走是一个速率较慢的 Lazy 随机游走,但仍然会收敛到稳态。Oono 和 Suzuki 等人于 ICLR 2020 发表的论文指出,当加入激活函数时,图神经网络收敛到稳态的速度乘指数形式,其收敛速度由图的拓扑结构决定。
GCNII:Simple and Deep Graph Convolutional Networks(ICML, 2020)
如上图所示,为了解决 GCN 存在的过平滑问题,魏哲巍教授团队通过初始值残差连接在每一层的图表示上加上初始特征,并且向每一层的权重中加入了单位映射,从而更多地保留了上一层的表示。
通过加入初始值残差,我们实现了「带重启」的随机游走,随机游走在每一步上有![]() 的概率返回初始状态,有
的概率返回初始状态,有![]() 的概率随机走向当前节点的任一邻居,此时稳态的分布就与起始节点有关了。这种随机游走与 PageRank 算法使用的方法类似。
的概率随机走向当前节点的任一邻居,此时稳态的分布就与起始节点有关了。这种随机游走与 PageRank 算法使用的方法类似。
受到马腾宇博士论文「Identity Matters in Deep Learning」的启发,我们向待学习的权重矩阵加入了单位矩阵,有效提升了模型的泛化能力。
优化函数:GNN Deep Unfolding
Cai 等人在 2020 年指出,GCN 实际上是在最小化狄利克雷能量:
其中,A 为邻接矩阵,z 为节点特征,d 为节点度数。狄利克雷能量可以衡量图满足同配性假设(邻居节点特征具有相关性)的程度。可以证明,GCN 的迭代实际上是狄利克雷能量优化函数的近端梯度下降算法。然而,狄利克雷能量可能迭代到 0(当节点 i 与节点 j 有连边时,![]() ),此时会失去初始特征,出现过平滑现象。
),此时会失去初始特征,出现过平滑现象。
为了防止狄利克雷能量迭代到 0,我们在目标函数中加入 L-2 正则项,在最小化狄利克雷能量同时,保证节点特征与初始特征保持一定的相似程度。加入上述正则项后,目标函数梯度为 0 时,节点特征的迭代式与 GCNII 统一。
Graph Neural Networks Inspired by Classical Iterative Algorithms(ICML, 2021)
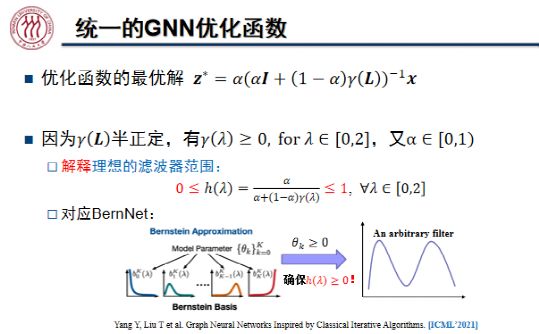
为了通过优化函数刻画更多的图模型、激活函数,寻找优化函数与滤波器、注意力机制之间的联系。魏哲巍教授团队在 ICML 2021 上发表了论文「Graph Neural Networks Inspired by Classical Iterative Algorithms」,提出了统一的 GNN 优化函数:
其中,半正定的![]() 为拉普拉斯矩阵的函数,其特征值
为拉普拉斯矩阵的函数,其特征值![]() ,从而保证了上述优化函数为凸函数。该框架非常灵活,当
,从而保证了上述优化函数为凸函数。该框架非常灵活,当![]() 时,狄利克雷能量函数变为了:
时,狄利克雷能量函数变为了:
该能量函数可以解释异配性假设:邻居节点的特征具有负相关性。当![]() 时,节点的表征为热核形式,可以用来解释 GDC、GraphHeat 的设计,优化函数的最优解为:
时,节点的表征为热核形式,可以用来解释 GDC、GraphHeat 的设计,优化函数的最优解为:
通过在优化函数中加入非负正则项![]() ,我们可以给 z 中小于 0 的项施加正无穷的惩罚。此时,近端算子对应于激活函数 ReLU。
,我们可以给 z 中小于 0 的项施加正无穷的惩罚。此时,近端算子对应于激活函数 ReLU。
如果我们通过![]() 对拉普拉斯矩阵进行特征值分解,相当于进行了滤波操作。当
对拉普拉斯矩阵进行特征值分解,相当于进行了滤波操作。当![]() 半正定时,图神经网络即为 BernNet。
半正定时,图神经网络即为 BernNet。
我们通过![]() 定义图中边的平滑程度,则该函数的切线斜率决定了 GAT 的注意力权重。基于上述思想,魏哲巍教授团队设计了新的 GNN 模型 TWIRLS,使用迭代重加权最小二乘法解该优化问题。
定义图中边的平滑程度,则该函数的切线斜率决定了 GAT 的注意力权重。基于上述思想,魏哲巍教授团队设计了新的 GNN 模型 TWIRLS,使用迭代重加权最小二乘法解该优化问题。
04
结语
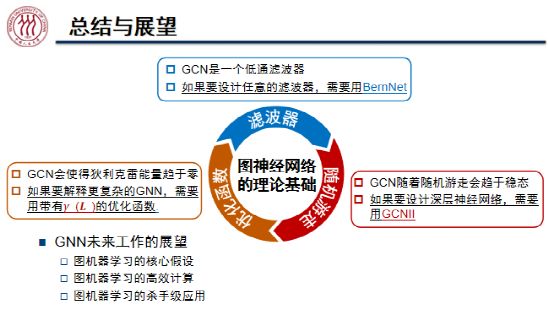
在本次演讲中,魏哲巍教授从滤波器、随机游走、优化函数三个角度介绍了图神经网络的理论基础,分析了 GCN 存在过平滑现象的原因,举例说明了如何针对性的对图神经网络进行改进,从而解决过平滑等问题,设计出更加高效的滤波器。
在魏哲巍教授看来,图机器学习有着非常广阔的研究前景。目前,图机器学习的核心假设尚不明确、可扩展性有待提高,期待出现图神经网络的「杀手级」应用。
欢迎点击阅读原文参与文章讨论。