理解LSTM和GRU
LSTM
- LSTM
-
- 介绍
-
- 结构
- 文档
- LSTM代码
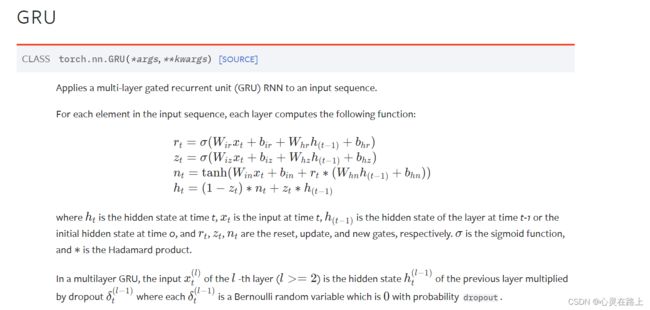
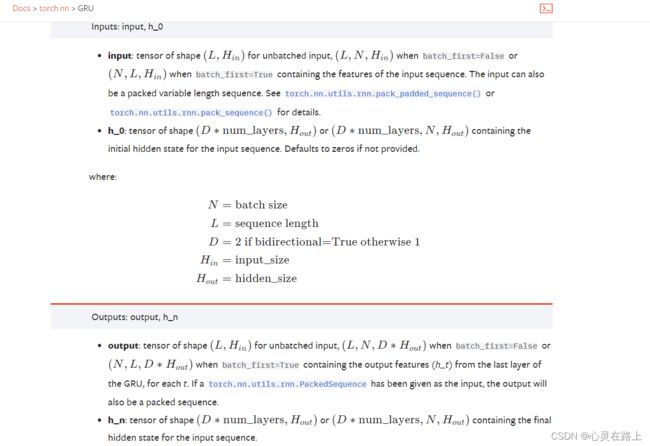
- GRU
-
- 介绍
- 流程
- 文档
- GRU代码
LSTM
介绍
参考链接: 【译】理解LSTM(通俗易懂版)
前面我们介绍了RNN的算法, 它处理时间序列的问题的效果很好, 但是仍然存在着一些问题, 其中较为严重的是容易出现梯度消失或者梯度爆炸的问题(BP算法和长时间依赖造成的). 注意: 这里的梯度消失和BP的不一样,这里主要指由于时间过长而造成记忆值较小的现象.
因此, 就出现了一系列的改进的算法, 这里介绍主要的两种算法: LSTM 和 GRU.
LSTM 和 GRU对于梯度消失或者梯度爆炸的问题处理方法主要是:
- 对于梯度消失: 由于它们都有特殊的方式存储”记忆”,那么以前梯度比较大的”记忆”不会像简单的RNN一样马上被抹除,因此可以一定程度上克服梯度消失问题。
- 对于梯度爆炸:用来克服梯度爆炸的问题就是gradient clipping,也就是当你计算的梯度超过阈值c或者小于阈值-c的时候,便把此时的梯度设置成c或-c。
那么为什么LSTM可以解决长期以来的问题?
因为LSTM中有两个通道在保持记忆:短期记忆h,保持非线性操作;长期记忆C,保持线性操作。因为线性操作是比较稳定的,所以C的变化相对稳定,保持了长期记忆。而对有用信息的长期记忆是通过训练获得的,也就是说在内部的几个权值矩阵中。
结构
LSTM的核心是细胞状态——最上层的横穿整个细胞的水平线,它通过门来控制信息的增加或者删除。
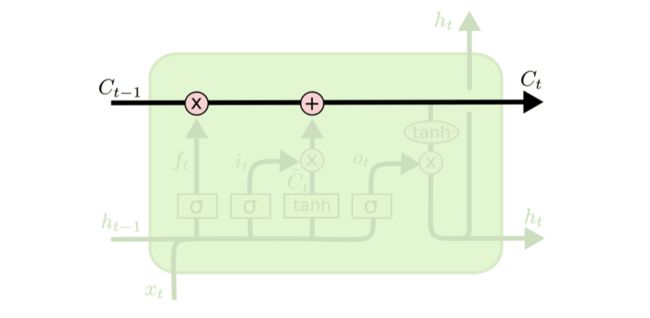 1、LSTM的第一步就是决定细胞状态需要丢弃哪些信息。这部分操作是通过一个称为忘记门的sigmoid单元来处理的。它通过查看 h t − 1 h_{t-1} ht−1和 x t x_t xt信息来输出一个0-1之间的向量,该向量里面的0-1值表示细胞状态 C t − 1 C_{t-1} Ct−1中的哪些信息保留或丢弃多少。0表示不保留,1表示都保留。忘记门如下图所示。
1、LSTM的第一步就是决定细胞状态需要丢弃哪些信息。这部分操作是通过一个称为忘记门的sigmoid单元来处理的。它通过查看 h t − 1 h_{t-1} ht−1和 x t x_t xt信息来输出一个0-1之间的向量,该向量里面的0-1值表示细胞状态 C t − 1 C_{t-1} Ct−1中的哪些信息保留或丢弃多少。0表示不保留,1表示都保留。忘记门如下图所示。
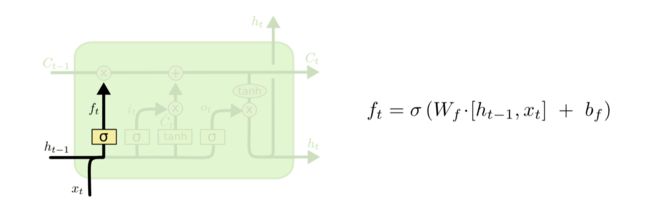
为什么可以选择忘记得信息,因为sigmoid函数的范围就是0-1,使用0表示丢弃,1表示保留。
2、下一步是决定给细胞状态添加哪些新的信息。这一步又分为两个步骤,首先,利用 h t − 1 h_{t-1} ht−1和 x t x_t xt通过一个称为输入门的操作来决定更新哪些信息。然后利用 h t − 1 h_{t-1} ht−1和 x t x_t xt通过一个tanh层得到新的候选细胞信息 C t ~ \tilde{C_t} Ct~,这些信息可能会被更新到细胞信息中。这两步描述如下图所示。

3、下面将更新旧的细胞信息 C t − 1 C_{t-1} Ct−1,变为新的细胞信息 C t C_t Ct。更新的规则就是通过忘记门选择忘记旧细胞信息的一部分,通过输入门选择添加候选细胞信息 C t ~ \tilde{C_t} Ct~的一部分得到新的细胞信息 C t C_t Ct。更新操作如下图所示
4、更新完细胞状态后需要根据输入的 h t − 1 h_{t-1} ht−1和 x t x_t xt来判断输出细胞的哪些状态特征,这里需要将输入经过一个称为输出门的sigmoid层得到判断条件,然后将细胞状态经过tanh层得到一个-1~1之间值的向量,该向量与输出门得到的判断条件相乘就得到了最终该RNN单元的输出。该步骤如下图所示
文档
LSTM代码
import torch
#准备数据
index_chart = ['e', 'h', 'l', 'o']
x_data = [1, 0, 2, 2, 3]
y_data = [1, 0, 0, 3, 2]
one_hot_lookup = [[1, 0, 0, 0], # 设置一个索引表
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]]
x_one_hot = [one_hot_lookup[x] for x in x_data]
input_size = 4
batch_size = 1
inputs = torch.Tensor(x_one_hot).view(-1, batch_size, input_size)
labels = torch.LongTensor(y_data).view(-1, 1) # 增加维度方便计算loss
#设计网络模型
class LSTM(torch.nn.Module):
# 进行基础设置
def __init__(self):
super(LSTM, self).__init__()
self.lineari = torch.nn.Linear(4, 4)
self.linearf = torch.nn.Linear(4, 4)
self.linearc = torch.nn.Linear(4, 4)
self.linearo = torch.nn.Linear(4, 4)
self.sigmoid = torch.nn.Sigmoid()
self.tanh = torch.nn.Tanh()
# 设置前向传播函数
def forward(self, x, hidden, C):
i = self.sigmoid(self.lineari(x) + self.lineari(hidden))
f = self.sigmoid(self.linearf(x) + self.linearf(hidden))
c = self.sigmoid(self.linearc(x) + self.linearc(hidden))
o = self.sigmoid(self.linearo(x) + self.linearo(hidden))
C = f * C + i * c # 候选状态x输入状态+遗忘状态x上一个细胞状态,得到此次细胞状态
hidden = o * self.tanh(C) # 此次得到的细胞状态进行激活后,再乘以输出门,最后得到隐藏层输出
return hidden, C
net = LSTM()
#计算损失和更新
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(), lr=0.03)
#进行训练和更新
for epoch in range(100):
loss = 0
optimizer.zero_grad() # 梯度每一次迭代完之后都要归零
hidden = torch.zeros(batch_size, input_size) # 初始的隐藏层的值均设置为0,形状为(batch_size,input_size)
C = torch.zeros(batch_size, input_size) # 初始的细胞状态值均设置为0,形状为(batch_size,input_size)
print('Predicten string:', end='')
for input, label in zip(inputs, labels):
hidden, C = net(input, hidden, C)
loss += criterion(hidden, label) # hidden.shape=(1,4) label.shape=1
_, idx = hidden.max(dim=1) # 从第一个维度上取出预测概率最大的值和该值所在序号,_代表其最大概率对应的值,idx代表该值所对应的索引序号
print(index_chart[idx.item()], end='') # 按上面序号输出相应字母字符
loss.backward()
optimizer.step()
print(', Epoch [%d/100] loss=%.4f' % (epoch + 1, loss.item()))
GRU
介绍
其实我觉得,只要理解了LSTM,GRU很好理解,只是变了一下内部结构。
GRU是什么
GRU即Gated Recurrent Unit。前面说到为了克服RNN无法很好处理远距离依赖而提出了LSTM,而GRU则是LSTM的一个变体,当然LSTM还有有很多其他的变体。GRU保持了LSTM的效果同时又使结构更加简单,所以它也非常流行。
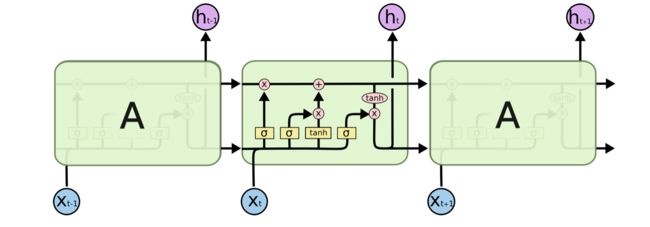
而GRU模型如下,它只有两个门了,分别为更新门和重置门,即图中的 z t z_t zt和 r t r_t rt。更新门用于控制前一时刻的状态信息被带入到当前状态中的程度,更新门的值越大说明前一时刻的状态信息带入越多。重置门用于控制忽略前一时刻的状态信息的程度,重置门的值越小说明忽略得越多。

图中的 zt 和 rt 分别表示更新门 (红色) 和重置门 (蓝色)。重置门 rt 控制着前一状态的信息 ht-1 传入候选状态 (图中带波浪线的ht) 的比例,重置门 rt 的值越小,则与 ht-1 的乘积越小,ht-1 的信息添加到候选状态越少。更新门用于控制前一状态的信息 ht-1 有多少保留到新状态 ht 中,当 (1- zt) 越大,保留的信息越多。
-
公式1就是遗忘的作用,看看之前的数据有多少重要的,不重要的都忘掉。
-
公式2和3是保留现在的状态。
-
公式4就是根据公式1得到的信号,对上一时刻和当前时刻的状态进行更新。
流程
首先,我们先通过上一个传输下来的状态 h t − 1 h_{t-1} ht−1和当前节点的输入 x t x^t xt来获取两个门控状态。如下图所示,其中 r r r控制重置的门控(reset gate), z z z为控制更新的门控(update gate)。

2、得到门控信号之后,首先使用重置门控来得到“重置”之后的数据 h t − 1 ′ = h t − 1 ∗ r h^{t-1}{'}=h^{t-1}*r ht−1′=ht−1∗r ,再将 h t − 1 ′ h^{t-1}{'} ht−1′与输入 x t x^t xt进行拼接,再通过一个tanh激活函数来将数据放缩到-1~1的范围内。即得到如下图2-3所示的 h ′ h^{'} h′

这里的 h ′ h^{'} h′主要是包含了当前输入的 x t x^{t} xt数据。有针对性地对 h ′ h^{'} h′添加到当前的隐藏状态,相当于”记忆了当前时刻的状态“。
最后介绍GRU最关键的一个步骤,我们可以称之为**”更新记忆“**阶段。
在这个阶段,我们同时进行了遗忘了记忆两个步骤。我们使用了先前得到的更新门控 z z z(update gate)。
更新表达式:
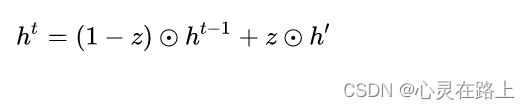
首先再次强调一下,门控信号(这里的 z z z)的范围为0~1。门控信号越接近1,代表”记忆“下来的数据越多;而越接近0则代表”遗忘“的越多。
GRU很聪明的一点就在于,我们使用了同一个门控 z z z就同时可以进行遗忘和选择记忆(LSTM则要使用多个门控)。
- 前半部分表示对原本隐藏状态的选择性“遗忘”。这里的 1 − z 1-z 1−z可以想象成遗忘门(forget gate),忘记 h t − 1 h_{t-1} ht−1维度中一些不重要的信息。
- 表示对包含当前节点信息的 h ′ h^{'} h′进行选择性”记忆“。与上面类似,这里的 1 − z 1-z 1−z同理会忘记 h ′ h^{'} h′维度中的一些不重要的信息。或者,这里我们更应当看做是对 h ′ h^{'} h′维度中的某些信息进行选择。
- 结合上述,这一步的操作就是忘记传递下来的 h t − 1 h_{t-1} ht−1中的某些维度信息,并加入当前节点输入的某些维度信息。
可以看到,这里的遗忘 z z z和选择 1 − z 1-z 1−z是联动的。也就是说,对于传递进来的维度信息,我们会进行选择性遗忘,则遗忘了多少权重 ( z z z),我们就会使用包含当前输入的 h ′ h^{'} h′中所对应的权重进行弥补 ( 1 − z ) (1-z) (1−z)。以保持一种”恒定“状态。
文档
GRU代码
import torch
input_size = 4
batch_size = 1
class GRU(torch.nn.Module):
def __init__(self):
super(GRU, self).__init__()
self.linearrx = torch.nn.Linear(4, 4)
self.linearzx = torch.nn.Linear(4, 4)
self.linearnx = torch.nn.Linear(4, 4)
self.linearrh = torch.nn.Linear(4, 4)
self.linearzh = torch.nn.Linear(4, 4)
self.linearnh = torch.nn.Linear(4, 4)
self.sigmoid = torch.nn.Sigmoid()
self.tanh = torch.nn.Tanh()
def forward(self, x, hidden):
r = self.sigmoid(self.linearrx(x) + self.linearrh(hidden))
z = self.sigmoid(self.linearzx(x) + self.linearzh(hidden))
n = self.tanh(self.linearnx(x) + r * self.linearnh(hidden))
hidden = (1 - z) * n + z * hidden
return hidden
net = GRU()
def train():
idx2char = ['e', 'h', 'l', 'o'] # 方便最后输出结果
x_data = [1, 0, 2, 2, 3] # 输入向量
y_data = [3, 1, 2, 3, 2] # 标签
one_hot_lookup = [[1, 0, 0, 0], # 查询ont hot编码 方便转换
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]]
x_one_hot = [one_hot_lookup[x] for x in x_data] # 按"1 0 2 2 3"顺序取one_hot_lookup中的值赋给x_one_hot
'''运行结果为x_one_hot = [ [0, 1, 0, 0],
[1, 0, 0, 0],
[0, 0, 1, 0],
[0, 0, 1, 0],
[0, 0, 0, 1] ]
刚好对应输入向量,也对应着字符值'hello'
'''
inputs = torch.Tensor(x_one_hot).view(-1, batch_size, input_size)
labels = torch.LongTensor(y_data).view(-1, 1) # 增加维度方便计算loss
# ---计算损失和更新
criterion = torch.nn.CrossEntropyLoss() # 交叉熵
optimizer = torch.optim.Adam(net.parameters(), lr=0.01)
# ---计算损失和更新
for epoch in range(100):#开始训练
loss = 0
optimizer.zero_grad()
hidden = torch.zeros(batch_size, input_size)#提供初始化隐藏层(h0)
print('Predicten string:', end='')
for input, label in zip(inputs,labels):#并行遍历数据集 一个一个训练
hidden = net(input, hidden)
loss += criterion(hidden, label)#hidden.shape=(1,4) label.shape=1
_, idx = hidden.max(dim=1)#从第一个维度上取出预测概率最大的值和该值所在序号
print(idx2char[idx.item()], end='')#按上面序号输出相应字母字符
loss.backward()
optimizer.step()
print(', Epoch [%d/100] loss=%.4f' %(epoch+1, loss.item()))