MotionFormer论文阅读
Keeping Your Eye on the Ball:Trajectory Attention in Video Transformers
- 任务
- 动机
- 目的
- 方法
-
- 序列化
- 视频自注意力的计算方式
- 轨迹注意力(Trajectory Attention)
-
- 维度变换说明
- 模型搭建

论文地址: https://arxiv.org/abs/2106.05392
任务
视频动作识别——Video Action Recognition
动机
传统的Video TRM对空间和时间token的处理方式是一样的,但这种方式是不妥当的,原因有如下两点:
- 视频相邻帧之间包含大量的冗余的空间信息,在视频中应用vanilla的self-attention机制,将会比较在所有可能的空间位置和帧中提取的成对图像块,这会导致它过多关注冗余的空间信息,而不是时间信息;
- 在第t帧的一个位置成像的物理点可能与在第t+k帧的该位置发现的完全无关,应该对这些时间对应进行建模,以便于了解动态场景。
现有的ViT模型在整个3D时空特征体上汇集信息,或者在时间维度上轴向汇集信息,忽略了物体点在时间维度上运动的轨迹,
简单来说,Vanilla Self-Attention不能克服视频空间信息的冗余并且无法关注到视频中物体运动的轨迹。
因此作者提出一种自注意的变体,称为轨迹注意(trajectory attention),这种变体Attention机制能够更好地描述视频中包含的时间信息。作者借鉴静态图像中最重要的归纳偏置——空间局部性,从而思考对视频,是否存在时间关联的更好的感应偏差?答案是确定的,作者认为,沿着运动轨迹池化,将为视频数据提供更自然的归纳偏置,并允许网络从同一物体或区域的多个视图聚合信息,以推断物体或区域如何移动 。
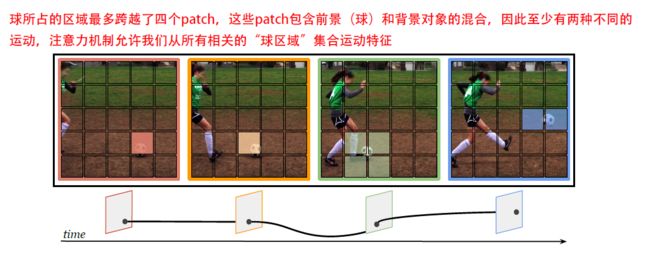
目的
修改transformers中的注意力机制,以更好地捕获视频中包含的信息。
方法
序列化
本文使用的token采集方法与ViViT中相似,将视频序列处理为ST个token的序列,其中S为空间分辨率,T为时间序列长度,使用Tubelet embedding进行3D embedding,Tubelet embedding可看做在3D层面上提取特征,定义非重叠的tube同时在空间和时间维度上进行线性映射,最终得到ST个维度为D的spatial-temporal token,即ST个 x s t ∈ R D x_{st}\in R^D xst∈RD。
具体可参考: ViViT中对视频序列token的两种构建方式。
然后需要在token中加入时间和空间的位置编码,即
z s t = x s t + e S s + e T t z_{st}=x_{st}+e_S^s+e^t_T zst=xst+eSs+eTt
最后加入用于分类的cls token z c l s z_{cls} zcls,将视频作为一个整体进行推理。
本模型的模块组成与ViT的类似,包含了LN、MHA、残差连接和feed-forward网络,如下
y = M H A ( L N ( z ) ) + z ; z ′ = M L P ( L N ( y ) ) + y y=MHA(LN(z))+z ;z'=MLP(LN(y))+y y=MHA(LN(z))+z;z′=MLP(LN(y))+y
视频自注意力的计算方式
论文首先介绍了TimesFormer中两种自注意力计算方式。
对视频产生的时空token,最易想到的做法是同时计算所有token之间的关联,
y s t = ∑ s ′ t ′ v s ′ t ′ e x p < q s t , k s ′ t ′ > ∑ s ˉ t ˉ e x p < q s t , k s ˉ t ˉ > y_{st}=\sum_{s't'}v_{s't'}\frac{exp
q s t q_{st} qst需要去匹配所有的 k s ′ t ′ k_{s't'} ks′t′这种方式其实就是TimesFormer中的Joint space-time attention,这种方式理论上效果会是最好的,但其复杂度为 O ( S 2 T 2 ) O(S^2T^2) O(S2T2)。
另一种视频自注意力计算方式是divided space-time attention:先做time上的att,每一个patch在时间上只做对应位置上的att,再做space上的att,每一个patch计算当前帧每一个位置的patch,如下所示
y s t = ∑ t ′ v s ′ t e x p < q s t , k s t ′ > ∑ t ˉ e x p < q s t , k s t ˉ > ( t i m e ) y_{st}=\sum_{t'}v_{s't}\frac{exp
y s t = ∑ s ′ v s ′ t e x p < q s t , k s ′ t > ∑ s ˉ e x p < q s t , k s ˉ t > ( s p a c e ) y_{st}=\sum_{s'}v_{s't}\frac{exp
这种方式将计算复杂度降低为 O ( S 2 T ) + O ( S T 2 ) O(S^2T)+O(ST^2) O(S2T)+O(ST2),两种计算方式的示意图如下:
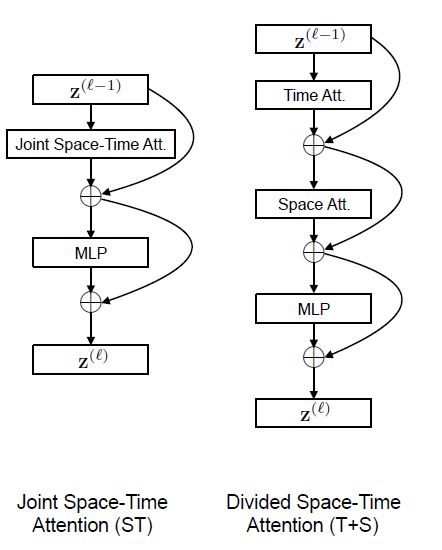
轨迹注意力(Trajectory Attention)
本文所提出的轨迹注意力(Trajectory Attention),大概的计算方式如下图:
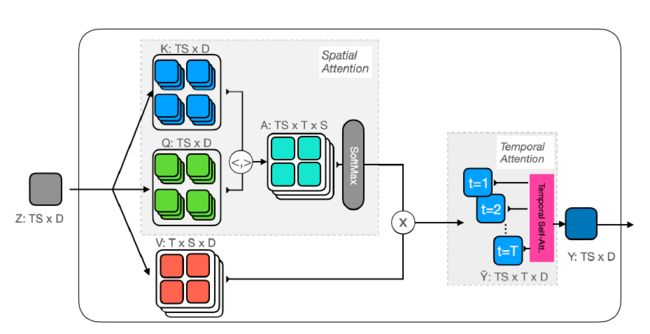
对于每个时空位置(轨迹参考点)和相应的查询 q q q,作者构造了一组轨迹token ,轨迹token拓展到视频序列的持续时间,其不同时间的轨迹token计算如下:
y ~ s t t ′ = ∑ s ′ v s ′ t ′ ⋅ exp ⟨ q s t , k s ′ t ′ ⟩ ∑ s ˉ exp ⟨ q s t , k s ˉ t ′ ⟩ \tilde{\mathbf{y}}_{s t t^{\prime}}=\sum_{s^{\prime}} \mathbf{v}_{s^{\prime} t^{\prime}} \cdot \frac{\exp \left\langle\mathbf{q}_{s t}, \mathbf{k}_{s^{\prime} t^{\prime}}\right\rangle}{\sum_{\bar{s}} \exp \left\langle\mathbf{q}_{s t}, \mathbf{k}_{\bar{s} t^{\prime}}\right\rangle} y~stt′=s′∑vs′t′⋅∑sˉexp⟨qst,ksˉt′⟩exp⟨qst,ks′t′⟩
上面的attention计算仅在空间上应用,并独立地应用于每一帧,然后在对空间上的维度进行求和(pooling),从而只剩下时间维度,表示不同轨迹参考点时间的轨迹。
在计算出轨迹表达后,需要进一步跨时间汇集它们。为此,轨迹token被投影到一组新的 queries, keys 和values上
q ~ s t = W ~ q y ~ s t t , k ~ s t t ′ = W ~ k y ~ s t t ′ , v ~ s t t ′ = W ~ v y ~ s t t ′ \tilde{\mathbf{q}}_{s t}=\tilde{\mathbf{W}}_{q} \tilde{\mathbf{y}}_{s t t}, \quad \tilde{\mathbf{k}}_{s t t^{\prime}}=\tilde{\mathbf{W}}_{k} \tilde{\mathbf{y}}_{s t t^{\prime}}, \quad \tilde{\mathbf{v}}_{s t t^{\prime}}=\tilde{\mathbf{W}}_{v} \tilde{\mathbf{y}}_{s t t^{\prime}} q~st=W~qy~stt,k~stt′=W~ky~stt′,v~stt′=W~vy~stt′
更新之后的查询 q ~ s t \tilde{q}_{st} q~st对应的是轨迹参考点,其包含来自所有帧空间汇集的信息,接着利用新的查询 q ~ s t \tilde{q}_{st} q~st在轨迹的维度上池化以获取一维注意力:
y s t = ∑ t ′ v ~ s t t ′ ⋅ exp ⟨ q ~ s t , k ~ s t t ′ ⟩ ∑ t ˉ exp ⟨ q ~ s t , k ~ s t t ˉ ⟩ \mathbf{y}_{s t}=\sum_{t^{\prime}} \tilde{\mathbf{v}}_{s t t^{\prime}} \cdot \frac{\exp \left\langle\tilde{\mathbf{q}}_{s t}, \tilde{\mathbf{k}}_{s t t^{\prime}}\right\rangle}{\sum_{\bar{t}} \exp \left\langle\tilde{\mathbf{q}}_{s t}, \tilde{\mathbf{k}}_{s t \bar{t}}\right\rangle} yst=t′∑v~stt′⋅∑tˉexp⟨q~st,k~sttˉ⟩exp⟨q~st,k~stt′⟩
维度变换说明
首先看空间注意力(Spatial Attention):它为每个时空位置ST形成一组ST轨迹token,这是一种类Joint Attention的操作,计算过程中维度变化如下图:
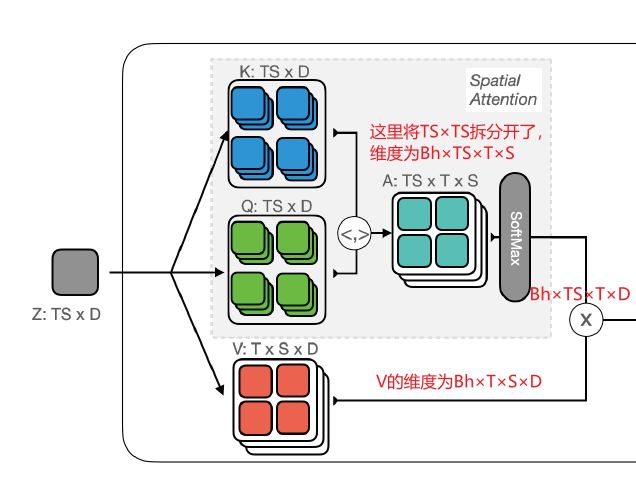
得到每个时空位置(文中称为轨迹参考点)在不同时间点的轨迹,维度为Bh×TS×T×D。
再看图中的Temporal Attention:明确的是,Temporal Attention的输入是Spatial Attention的输出,维度为Bh×TS×T×D。
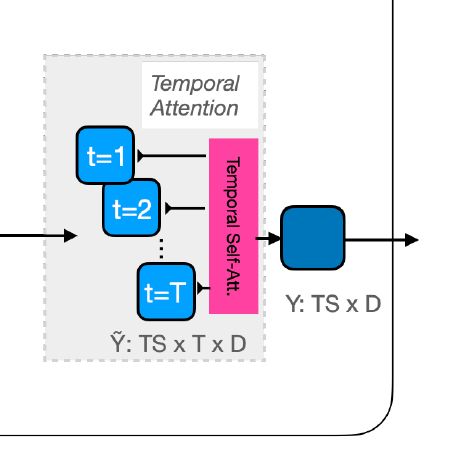
Temporal Attention沿着这些轨迹进行1D时间注意操作,通过这种方式,沿着视频中对象的运动路径积累信息。
Temporal Attention同样需要一组q,k,v
为方便获取qkv,首先将维度变换为Bh×TS×T×D → \rightarrow →B×TS×T×Dh,对得到的张量,做映射可获取k与v:B×h×TS×T×D;
再次进行维度变化B×TS×T×Dh → \rightarrow →B×T×S×T×Dh,对得到的张量执行diagonal操作,从T×T维度之间取一个token,即每帧取一个token,将维度转变为B×T×S×T×Dh → \rightarrow →B×S×Dh×T;
再次做维度变化B×S×Dh×T → \rightarrow →B×h×TS×D,得到q。
q与k做操作,得到Attention矩阵:B×h×TS×T,最终输出为B×h×TS×D → \rightarrow →B×TS×Dh
总结如下:
Q u e r y : B × h × T S × D ; K e y / V a l u e : B × h ; A t t n : B × h × T S × T ; O u t : B × h × T S × D → B × T S × D h Query: B \times h \times T S \times D; \mathrm{K e y / V a l u e : ~ B × h}; Attn:B \times h \times T S \times T; Out:\mathrm{B} \times \mathrm{h} \times \mathrm{TS} \times \mathrm{D} \rightarrow \mathrm{B} \times \mathrm{TS} \times \mathrm{Dh} Query:B×h×TS×D;Key/Value: B×h;Attn:B×h×TS×T;Out:B×h×TS×D→B×TS×Dh
这种计算的方式在空间和时间上均具有二次的复杂度,没有计算的优势,并且比时空分离的注意力计算方式要更慢,因此作者提出了一种近似注意力机制来加速计算。
