原笔迹手写实现平滑和笔锋效果之:笔迹的平滑(一)

点击上方“AI搞事情”关注我们

---

---

> 本文转载自：

https://www.cnblogs.com/zl03jsj/p/8047259.html

---

之前研究过一种用于 模拟真实 手写笔迹签名 的算法,  要求能够保持原笔迹平滑,并有笔锋的效果.

在网上看了一些资料, 资料很多, 能够达到用于正式产品中的效果的一个都没有找到.

我看到最靠谱的一篇文章是这个:Interpolation with Bezier Curves

但是即使按照这篇文章讲的方法去实现手写笔迹, 表现的效果也非常的不理想.

而且, 这篇文章还只是涉及到了笔迹平滑的问题, 没有涉及到如何解决笔锋的问题

经过我一段时间的研究, 终于在上厕所的时候(有没有被duang了一下的感觉, 哈哈~O(∩_∩)O), 想出来了一种方法..先给大家展示两张在正式产品中的效果图:

前面两张图片是在手机上测试的效果,后面两张是在电脑上用鼠标写出来的效果.

 

当然, 必须承认, 图片中展示的效果效果的文字, 我反复写了很多次...随便画几条线大概是这样:

我将要介绍的这种算法, 还可以通过对某些参数的修改,  模拟出毛笔, 钢笔, 签字笔等各种笔...真实书写效果....

 

如果你还对贝塞尔曲线不了解, 我推荐查看这篇文章:史上最全的贝塞尔曲线(Bezier)全解,   所以, 在这里我会假设读者已经对Bezier曲线已经比较了解.

本文主要讲解 如何通过已知所有笔迹点, 计算出控制点, 使用3次bezier曲线拟合笔迹, 达到笔迹平滑的效果, 解决笔迹平滑的问题,.

除了本篇文章意外, 后面应该还会有两篇文章:

第二篇:介绍自己开发的一种笔迹拟合算法.

第三篇:主要介绍实现笔锋的效果.并提供最终的c++对此算法的实现的源代码和演示程序.

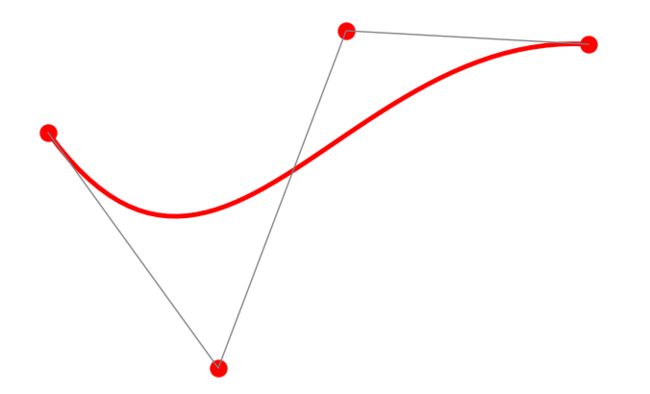
 Bezier曲线是通过简单地指定端点和中间的控制点(Control Point)来描绘出一条光滑的曲线, 三次贝塞尔曲线的效果是图片中这样:

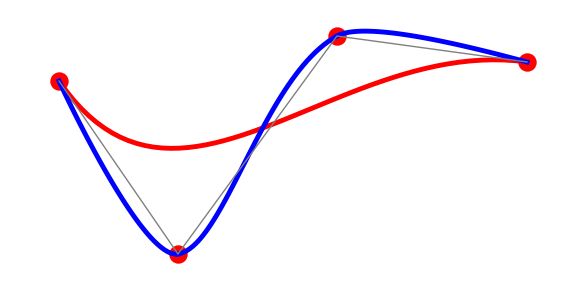
当红色的圆点代表原笔迹点时, 想必大家想要的效果是下面图片中的蓝色线条, 而不是红色线条吧:

贝赛尔曲线拟合会经过前后两个端点, 但不会经过中间的控制点,所以, 我们通过贝塞尔曲线来拟合笔迹点的时候, 是要:

对于所有的笔迹点, 每相邻的一对笔迹点作为前后端点来绘制Bezier曲线, 所有我们需要找出一些满足某种规律的点作为这些端点中间的控制点.

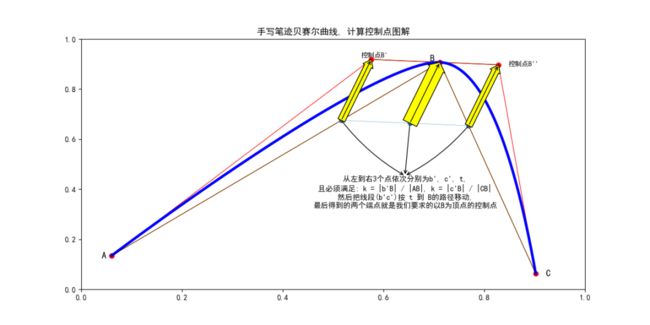
下面请看下图:

图中, 点A, B, C为我们的原笔迹点, B' 和 B''为我们计算出来的控制点.

计算控制点的方法是:

1) 设定一个0到1的系数k,  在AB和BC上找到两点, b'和c', 使得距离比值, Bb' / AB = Bc' / BC = k  , 计算出两个点 b' 和 c'..(k的大小决定控制点的位置,最终决定笔迹的平滑程度, k越小, 笔迹越锐利; k越大,则笔迹越平滑.)

2) 然后在b' c'这条线段上再找到一个点 t, 且线段的长度满足比例: b't / tc' = AB / BC,

3) 把b' 和 c', 沿着 点 t 到 点B的方向移动, 直到 t 和 B重合. 由b'移动后得到 B', 由 c'移动后的距离得到B'', B'和B''就是我们要计算的位于顶点B附近的两个控制点.

实际项目过程中, 使用下面的规则进行绘制笔迹:

1) 当我们在手写原笔迹绘制的时候, 得到第3个点(假设分别为ABC)的时候, 可以计算出B点附近的两个控制点., 由于是点A为起始点,, 所以直接把点A作为第一个控制点, 计算出来的B'作为第二个控制点,  这样AAB'B 4个点,就可以画出点A到点B的平滑贝塞尔曲线.(或者可以直接把AB'B这3个点, 把B'作为控制点, 用二次贝塞尔曲线来拟合, 也是可以的哦~.)

2) 当得到第4个点(假设为D)的时候, 我们通过BCD, 计算出在点C附近的两个控制点, C'和C'', 通过BB''C'C绘制出B到C的平滑曲线..

3) 当得到第i个点的时候, 进行第2个步骤.........

4) 当得到最后一个点Z的时候,  直接把Z作为第二个控制点(假设前一个点为Y),  即, 使用YY'ZZ来绘制Bezier曲线.

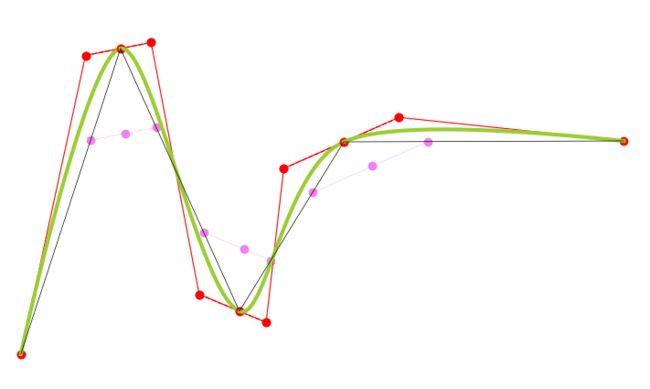
为了让阅读者能够更好的理解, 用Python实现了这个算法, 鼠标点击空白处可以增加笔迹点, 选中笔迹点可以动态拖动, 单击已有笔迹点执行删除:

效果图如下:

Python代码我就不再解释了, 直接提供出来:

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as np
from scipy.special import comb, perm
import matplotlib.pyplot as plt


plt.rcParams['font.sans-serif'] = ['SimHei']
# plt.rcParams['font.sans-serif'] = ['STXIHEI']
plt.rcParams['axes.unicode_minus'] = False


class Handwriting:
    def __init__(self, line):
        self.line = line
        self.index_02 = None    # 保存拖动的这个点的索引
        self.press = None       # 状态标识，1为按下，None为没按下
        self.pick = None        # 状态标识，1为选中点并按下,None为没选中
        self.motion = None      # 状态标识，1为进入拖动,None为不拖动
        self.xs = list()        # 保存点的x坐标
        self.ys = list()        # 保存点的y坐标
        self.cidpress = line.figure.canvas.mpl_connect('button_press_event', self.on_press)  # 鼠标按下事件
        self.cidrelease = line.figure.canvas.mpl_connect('button_release_event', self.on_release)  # 鼠标放开事件
        self.cidmotion = line.figure.canvas.mpl_connect('motion_notify_event', self.on_motion)  # 鼠标拖动事件
        self.cidpick = line.figure.canvas.mpl_connect('pick_event', self.on_picker)  # 鼠标选中事件


        self.ctl_point_1 = None


    def on_press(self, event):  # 鼠标按下调用
        if event.inaxes != self.line.axes: return
        self.press = 1


    def on_motion(self, event):  # 鼠标拖动调用
        if event.inaxes != self.line.axes: return
        if self.press is None: return
        if self.pick is None: return
        if self.motion is None:  # 整个if获取鼠标选中的点是哪个点
            self.motion = 1
            x = self.xs
            xdata = event.xdata
            ydata = event.ydata
            index_01 = 0
            for i in x:
                if abs(i - xdata) < 0.02:  # 0.02 为点的半径
                    if abs(self.ys[index_01] - ydata) < 0.02: break
                index_01 = index_01 + 1
            self.index_02 = index_01
        if self.index_02 is None: return
        self.xs[self.index_02] = event.xdata  # 鼠标的坐标覆盖选中的点的坐标
        self.ys[self.index_02] = event.ydata
        self.draw_01()


    def on_release(self, event):  # 鼠标按下调用
        if event.inaxes != self.line.axes: return
        if self.pick is None:  # 如果不是选中点，那就添加点
            self.xs.append(event.xdata)
            self.ys.append(event.ydata)
        if self.pick == 1 and self.motion != 1:  # 如果是选中点，但不是拖动点，那就降阶
            x = self.xs
            xdata = event.xdata
            ydata = event.ydata
            index_01 = 0
            for i in x:
                if abs(i - xdata) < 0.02:
                    if abs(self.ys[index_01] - ydata) < 0.02: break
                index_01 = index_01 + 1
            self.xs.pop(index_01)
            self.ys.pop(index_01)
        self.draw_01()
        self.pick = None  # 所有状态恢复，鼠标按下到稀放为一个周期
        self.motion = None
        self.press = None
        self.index_02 = None


    def on_picker(self, event):  # 选中调用
        self.pick = 1


    def draw_01(self):  # 绘图
        self.line.clear()  # 不清除的话会保留原有的图
        self.line.set_title('Bezier曲线拟合手写笔迹')
        self.line.axis([0, 1, 0, 1])  # x和y范围0到1
        # self.bezier(self.xs, self.ys)  # Bezier曲线
        self.all_curve(self.xs, self.ys)
        self.line.scatter(self.xs, self.ys, color='b', s=20, marker="o", picker=5)  # 画点
        self.line.plot(self.xs, self.ys, color='black', lw=0.5)  # 画线
        self.line.figure.canvas.draw()  # 重构子图


    # def list_minus(self, a, b):
    #     list(map(lambda x, y: x - y, middle, begin))


    def controls(self, k, begin, middle, end):
        # if k > 0.5 or k <= 0:
        #     print('value k not invalid, return!')
        #     return


        diff1 = middle - begin
        diff2 = end - middle


        l1 = (diff1[0] ** 2 + diff1[1] ** 2) ** (1 / 2)
        l2 = (diff2[0] ** 2 + diff2[1] ** 2) ** (1 / 2)


        first = middle - (k * diff1)
        second = middle + (k * diff2)


        c = first + (second - first) * (l1 / (l2 + l1))


        # self.line.text(begin[0] - 0.2, begin[1] + 1.5, 'A', fontsize=12, verticalalignment="top",
        #                horizontalalignment="left")
        # self.line.text(middle[0] - 0.2, middle[1] + 1.5, 'B', fontsize=12, verticalalignment="top",
        #                horizontalalignment="left")
        # self.line.text(end[0] + 0.2, end[1] + 1.5, 'C', fontsize=12, verticalalignment="top",
        #                horizontalalignment="left")
        # xytext = [(first[0] + second[0]) / 2, min(first[1], second[1]) - 10]
        #
        arrow_props = dict(arrowstyle="<-", connectionstyle="arc3")
        # self.line.annotate('', first, xytext=xytext, arrowprops=dict(arrowstyle="<-", connectionstyle="arc3,rad=-.1"))
        # self.line.annotate('', c, xytext=xytext, arrowprops=arrow_props)
        # self.line.annotate('', second, xytext=xytext, arrowprops=dict(arrowstyle="<-", connectionstyle="arc3,rad=.1"))


        # label = '从左到右3个点依次分别为b\', c\', t,\n' \
        #         '满足条件 k = |b\'B| / |AB|, k = |c\'B| / |CB|\n' \
        #         '然后把线段(b\'c\')按 t 到 B的路径移动,\n' \
        #         '最后得到的两个端点就是我们要求的以B为顶点的控制点'
        # self.line.text(xytext[0], xytext[1], label, verticalalignment="top", horizontalalignment="center")
        self.line.plot([first[0], c[0], second[0]], [first[1], c[1], second[1]], linestyle='dashed', color='violet', marker='o', lw=0.3)


        first_control = first + middle - c
        second_control = second + middle - c


        # self.line.text(first_control[0] - 0.2, first_control[1] + 1.5, '控制点B\'', fontsize=9, verticalalignment="top",
        #                horizontalalignment="left")
        # self.line.text(second_control[0] + 0.2, second_control[1] + 1.5, '控制点B\'\'', fontsize=9,
        #                verticalalignment="top", horizontalalignment="left")
        x_s = [first_control[0], second_control[0]]
        y_s = [first_control[1], second_control[1]]


        # self.line.annotate('', xy=middle, xytext=c, arrowprops=dict(facecolor='b' headlength=10, headwidth=25, width=20))
        arrow_props['facecolor'] = 'blue'
        # arrow_props['headlength'] = 5
        # arrow_props['headwidth'] = 10
        # arrow_props['width'] = 5
        # self.line.annotate('', xy=c, xytext=middle, arrowprops=arrow_props)
        # self.line.annotate('', xy=first, xytext=first_control, arrowprops=arrow_props)
        # self.line.annotate('', xy=second, xytext=second_control, arrowprops=arrow_props)
        # self.line.plot([begin[0], middle[0], end[0]], [begin[1], middle[1], end[1]], lw=1.0, marker='o')
        self.line.plot(x_s, y_s, marker='o', lw=1, color='r', linestyle='dashed')
        # self.line.plot(x_s, y_s, lw=1.0)


        return first_control, second_control


    def all_curve(self, xs, ys):
        self.ctl_point_1 = None
        le = len(xs)
        if le < 3: return


        begin = [xs[0], ys[0]]
        middle = [xs[1], ys[1]]
        end = [xs[2], ys[2]]
        self.one_curve(begin, middle, end)


        for i in range(3, le):
            begin = middle
            middle = end
            end = [xs[i], ys[i]]
            self.one_curve(begin, middle, end)


        end = [xs[le - 1], ys[le - 1]]
        x = [middle[0], self.ctl_point_1[0], end[0]]
        y = [middle[1], self.ctl_point_1[1], end[1]]
        self.bezier(x, y)


    def one_curve(self, begin, middle, end):
        ctl_point1 = self.ctl_point_1


        begin = np.array(begin)
        middle = np.array(middle)
        end = np.array(end)


        ctl_point2, self.ctl_point_1 = self.controls(0.3, np.array(begin), np.array(middle), np.array(end))
        if ctl_point1 is None: ctl_point1 = begin


        xs = [begin[0], ctl_point1[0], ctl_point2[0], middle[0]]
        ys = [begin[1], ctl_point1[1], ctl_point2[1], middle[1]]
        self.bezier(xs, ys)


        # xs = [middle[0], self.ctl_point_1[0], end[0], end[0]]
        # ys = [middle[1], self.ctl_point_1[1], end[1], end[1]]
        # self.bezier(xs, ys)


    def bezier(self, *args):  # Bezier曲线公式转换，获取x和y
        t = np.linspace(0, 1)  # t 范围0到1
        le = len(args[0]) - 1


        self.line.plot(args[0], args[1], marker='o', color='r', lw=0.8)
        le_1 = 0
        b_x, b_y = 0, 0
        for x in args[0]:
            b_x = b_x + x * (t ** le_1) * ((1 - t) ** le) * comb(len(args[0]) - 1, le_1)  # comb 组合，perm 排列
            le = le - 1
            le_1 = le_1 + 1


        le = len(args[0]) - 1
        le_1 = 0
        for y in args[1]:
            b_y = b_y + y * (t ** le_1) * ((1 - t) ** le) * comb(len(args[0]) - 1, le_1)
            le = le - 1
            le_1 = le_1 + 1


        color = "yellowgreen"
        if len(args) > 2 : color = args[2]
        self.line.plot(b_x, b_y, color=color, linewidth='3')


fig = plt.figure(2, figsize=(12, 6))
ax = fig.add_subplot(111)  # 一行一列第一个子图
ax.set_title('手写笔迹贝赛尔曲线, 计算控制点图解')


handwriting = Handwriting(ax)
plt.xlabel('X')
plt.ylabel('Y')


# begin = np.array([20, 6])
# middle = np.array([30, 40])
# end = np.array([35, 4])
# handwriting.one_curve(begin, middle, end)
# handwriting.controls(0.2, begin, middle, end)
plt.show()

大家可能觉得这个算法已经比较完美了, 下面我指出这种算法在实际使用中, 几个问题,  其中一些让人完全不能接受:

1) 在实际交互过程中, 这种方法需要3次贝塞尔曲线来拟合, 用户输入完第3个点,才能绘制第一条曲线, 第4个点才能绘制第2条曲线, 这种反馈不及时, 让体验非常差.

2) 每次都要计算控制点, 非常麻烦, 并且还影响效率.

在下一篇文章中, 我会介绍自己实现的解决了这些缺点的一种算法.

长按二维码关注我们

有趣的灵魂在等你