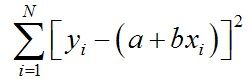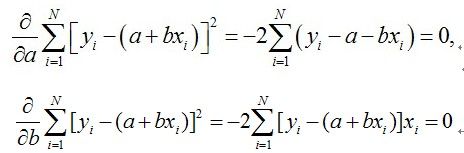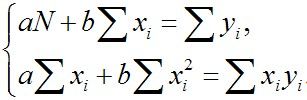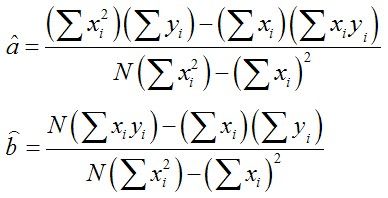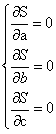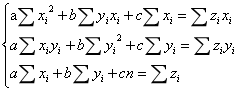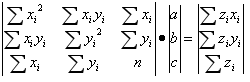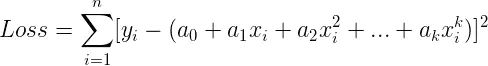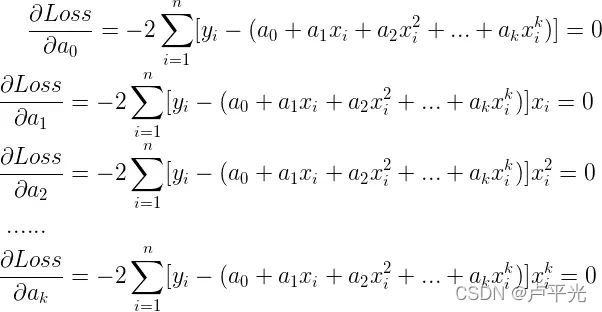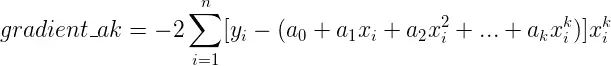最小二乘与极大似然估计
两者思想的差异
最小二乘估计与极大似然估计都是用来样本值来估计真实值的，之所以需要估计，是因为用数学量化真实世界事物关系时总是存在误差。
-
我们尽管痛苦的承认了有不能解释的误差，但是我们依然想尽可能的让这种『不被解释』的误差程 度最小，于是我们就想最小化区种不被解程的程度。因为点可能在线的上面或者下面，故而距离有 正有负，取绝对值又大麻烦，于是我们就直接把每个距旁都取一个平方变成正的，然后试图找出一 个距离所有点的距离的平方最小的这条线 这就是最小二乖法°、了，简单粗暴而有效。
-
而极大似然则更加的有哲理一些。还用上面的例子，我们观察到了三个点，于是我们开 什么我们观察到的是这三个点而不是另外三个？大千世界，去云众生，这么多人都有不后 不同的学历，但是偏偏这三个点让我给观察到了。这肯定说明了某种世界的真相。什么世界的真相呢？因为我们观案到了这三个点，反过来说，冥冥之中注定了这三个点被我们观察 到的概率可能是最大的。所以我们希望找到一个特定的底新和教育增量新水的组合，让我们观祭到 这三个点的概率最大，这个找的过程就是极大似然估计。
总结一句话：最小二乖法的核心是权衡，因为你要在很多条线中间选择，选择出距离所有的点之 最短的;而极大似然的核心是自恋，要相信自己是天选之子，自己看到的，就是冥冥之中最接近1真相的。
最小二乘法
拟合二维直线
用最小二乘拟合直线的例子很常见，例如直线：y＝a+bx
根据最小二乘思想，无法使根据大量样本（x，y点对），估计a、b，即可拟合出直线方程
计算过程：
-
写出误差平方公式
-
对a、b分别求偏导
-
解算a、b即可获得拟合的直线方程
拟合三维平面
三维直线不容易表示（两平面交线），所以拟合平面来看下最小二乘如何工作
通常三维平面表示为：ax + by + cz +d =0
-
将其转化为：z = ax + by + c
-
误差平方公式：
-
计算误差最小时的a、b、c即计算该方程的极值，求偏导：
即：
-
将其改为矩阵方程,得：
-
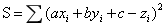
求解该恰定方程即可得到a，b，c。上述方程也可以用AX=b表示，该方程可以通过两边同时乘以系数矩阵的逆矩阵求得，即X=A-1Ab
极大似然估计
两者的一致性
最大似然估计和最小二乘法怎么理解
非线性情况的最小二乘与极大似然求解–Levenberg-Marquardt算法
无论是最小二乘还是极大似然估计，最终都希望通过求解方程组或者矩阵求逆（无直接逆矩阵则需要SVD分解）。但是针对非线性方程组，是无法计算求解的，此时需要例如高斯牛顿法或者LM法,通过迭代计算逼近真实方程解。
最速梯度法
例如拟合如下样本点构成曲线方程：
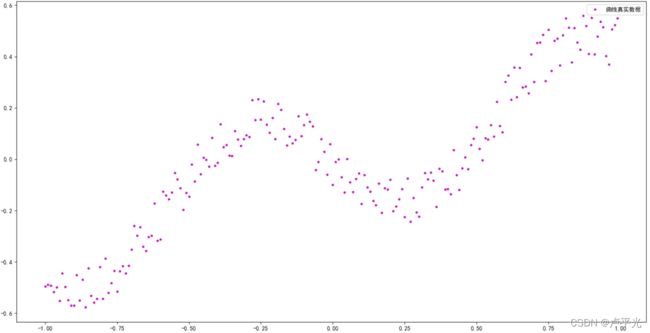
该数据实际是由：
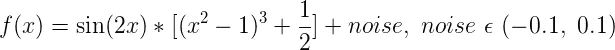
添加部分噪声生成的，此时，假设方程参数位置，利用最小二乘进行求解：
-
在写出误差函数前，先写出原函数的泰勒级数展开式
-
此时的误差函数（机器学习里称为损失函数）
-
分别对各系数求偏导
-
此时若不直接求解方程组，则可选用梯度下降法，迭代逼近真实的ai各系数：
-
（1）初始化k个系数值，开始迭代
-
（2）每次迭代，分别求出各个系数ak对应的梯度值
-
（3）用梯度值和学习率来更新每一个系数ak
-
（4）保证每次更新完所有系数，对应的损失函数值都在减少（说明梯度一直在下降）
-
-
有了梯度与损失函数，就可以愉快的使用梯度下降法估计系数了：
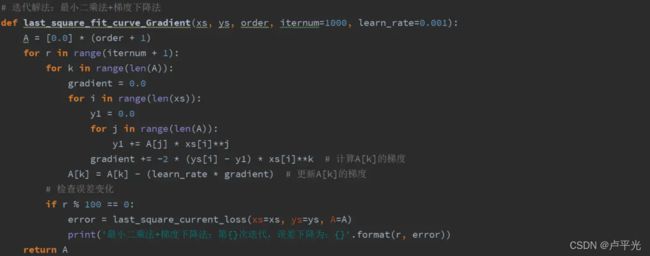
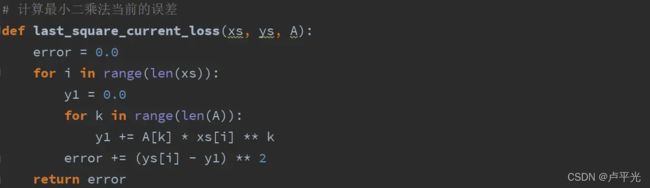
梯度下降法代码实现
考虑到最速下降法只能得到局部解，因此最小二乘问题可使用高斯牛顿法进行迭代近似获取全局最优解：
曲线拟合-高斯牛顿法
实例讲解高斯牛顿法
结合最速下降法与高斯牛顿法的各自有点，因此出现了优化的LM算法参考：
最优化方法（梯度下降、牛顿法、高斯牛顿法、LM算法）
Levenberg-Marquardt算法讲解
关键代码讲解
代码实现
重投影误差优化中LM算法的使用
特殊样本的估计–RANSAC
任何数据集都是用最小二乘去拟合并不合适，例如下图中存在大量“坏点”（即与真实样本偏差较大，不可信的点数据），此时使用最小二乘，则会全盘兼顾，反而降低里真实数据的影响力，因此需要一种方式，来评价那些数据并不真实，应予以剔除，这既是随机抽样一致性思想RANSAC
关于RANSAC的理解
代码实现