重建丢失的数据
目录
介绍
线性内插法
样条插值
使用抗锯齿过滤器进行重采样
缺失样本的重采样
重建大缺口
用局部估计重建间隙
介绍
随着廉价数据采集硬件的出现,你经常可以获得以固定间隔快速采样的信号。这允许获得对基础信号的精确近似。但是,当测量的数据被粗略采样或丢失重要部分时,会发生什么情况呢?如何推断已知样本之间各点的信号值?
线性内插法
线性插值是目前最常用的推断采样点之间的值的方法。默认情况下,当在MATLAB中绘制向量时,会看到用直线连接的点。为了逼近真实信号,需要对信号进行非常细致的采样。
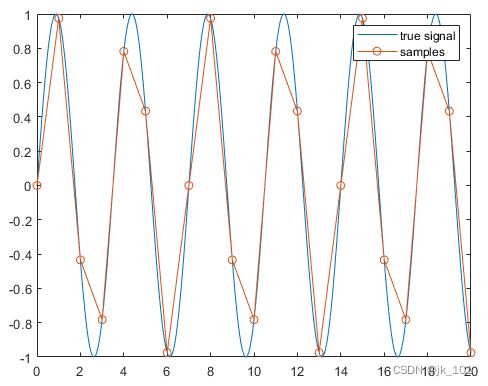
在本例中,正弦曲线以精细和粗略分辨率进行采样。当绘制在图上时,精细采样的正弦曲线非常类似于真正的连续正弦曲线。因此,可以将它用作“真实信号”的模型在下图中,粗采样信号的样本显示为由直线连接的圆圈。
tTrueSignal = 0:0.01:20;
xTrueSignal = sin(2*pi*2*tTrueSignal/7);
tSampled = 0:20;
xSampled = sin(2*pi*2*tSampled/7);
plot(tTrueSignal,xTrueSignal,'-', ...
tSampled,xSampled,'o-')
legend('true signal','samples')如图所示:
以同样的方式恢复中间样本是简单的plot执行插值。这可以用的线性方法来实现interp1功能。
tResampled = 0:0.1:20;
xLinear = interp1(tSampled,xSampled,tResampled,'linear');
plot(tTrueSignal,xTrueSignal,'-', ...
tSampled, xSampled, 'o-', ...
tResampled,xLinear,'.-')
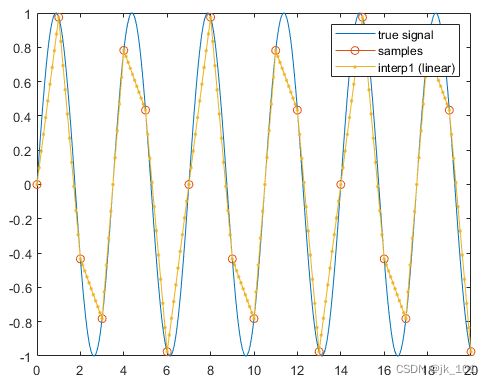
legend('true signal','samples','interp1 (linear)')如图所示:
线性插值的问题是结果不是很平滑。其他插值方法可以产生更平滑的近似值。
样条插值
许多物理信号类似于正弦曲线,因为它们是连续的,并且具有连续的导数。可以使用三次样条插值来重建此类信号,这样可以确保插值信号的一阶和二阶导数在每个数据点都是连续的:
xSpline = interp1(tSampled,xSampled,tResampled,'spline');
plot(tTrueSignal,xTrueSignal,'-', ...
tSampled, xSampled,'o', ...
tResampled,xLinear,'.-', ...
tResampled,xSpline,'.-')
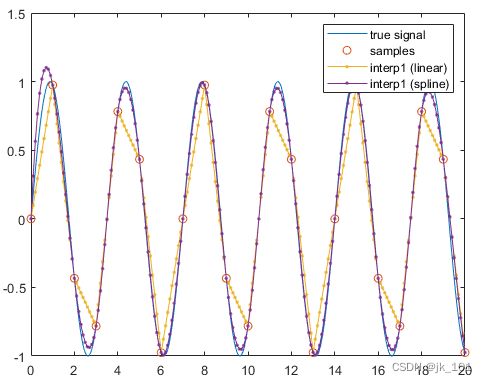
legend('true signal','samples','interp1 (linear)','interp1 (spline)')如图所示:
当对由正弦波组成的信号进行插值时,三次样条特别有效。然而,还有其他技术可用于获得对物理信号的更大保真度,这些物理信号具有高达非常高阶的连续导数。
使用抗锯齿过滤器进行重采样
这resample函数提供了另一种填充缺失数据的技术。resample能够以非常低的失真重建低频正弦分量。
xResample = resample(xSampled, 10, 1);
tResample = 0.1*((1:numel(xResample))-1);
plot(tTrueSignal,xTrueSignal,'-', ...
tResampled,xSpline,'.', ...
tResample, xResample,'.')
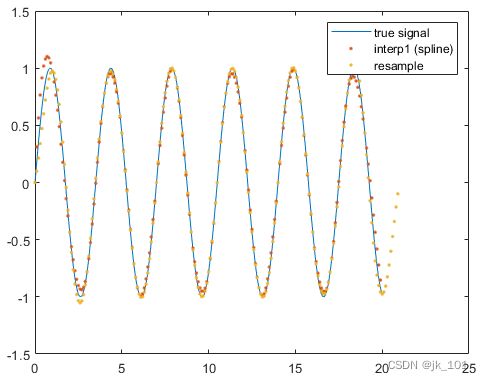
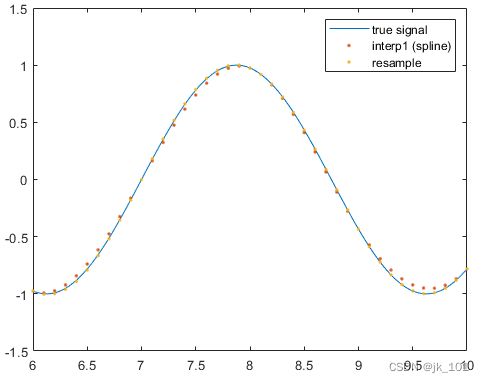
legend('true signal','interp1 (spline)','resample')如图所示:
像其他方法一样,resample重建端点有些困难。另一方面,重构信号的中心部分与真实信号非常一致。
xlim([6 10])如图所示:
缺失样本的重采样
resample可以适应非均匀采样的信号。当信号以高速率采样时,这种技术效果最佳。
在下面的例子中,我们创建一个缓慢移动的正弦曲线,删除一个样本,并放大到丢失样本的附近。
tTrueSignal = 0:.1:20;
xTrueSignal = sin(2*pi*2*tTrueSignal/15);
Tx = 0:20;
Tmissing = Tx(10);
Tx(10) = [];
x = sin(2*pi*2*Tx/15);
Xmissing = sin(2*pi*2*Tmissing/15);
[y, Ty] = resample(x,Tx,10,'spline');
plot(tTrueSignal, xTrueSignal, '-', ...
Tmissing,Xmissing,'x ', ...
Tx,x,'o ', ...
Ty,y,'. ')
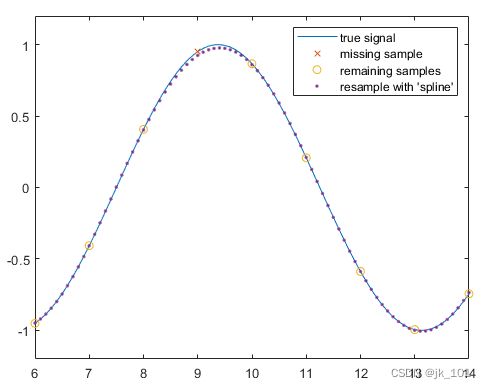
legend('true signal','missing sample','remaining samples','resample with ''spline''')
ylim([-1.2 1.2])
xlim([6 14])如图所示:
重构的正弦曲线相当好地跟踪真实信号的形状,在丢失样本附近只有微小的误差。
然而,resample当信号中有大的间隙时,不能很好地工作。例如,考虑中间部分缺失的阻尼正弦波:
tTrueSignal = (0:199)/199;
xTrueSignal = exp(-0.5*tTrueSignal).*sin(2*pi*5*tTrueSignal);
tMissing = tTrueSignal;
xMissing = xTrueSignal;
tMissing(50:140) = [];
xMissing(50:140) = [];
[y,Ty] = resample(xMissing, tMissing, 200, 'spline');
plot(tTrueSignal,xTrueSignal,'-', ...
tMissing,xMissing,'o',...
Ty,y,'.')
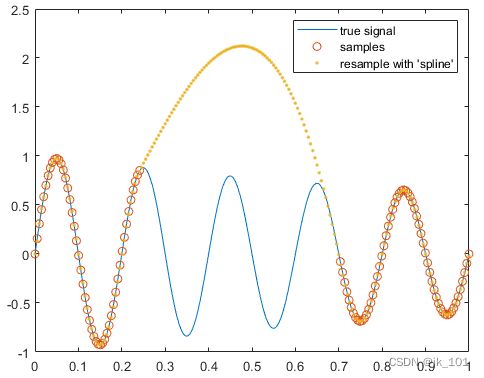
legend('true signal','samples','resample with ''spline''')如图所示:
这里resample确保重建的信号是连续的,并且在缺失点附近具有连续的导数。然而,它不能充分地重建丢失的部分。
重建大缺口
从上面可以看出,单独的滤波和三次插值可能不足以处理大的间隙。然而,对于某些类型的采样信号,例如观察振荡现象时出现的信号,通常可以根据间隙前后的数据来推断缺失样本的值。
这fillgaps函数可以替换丢失的样本(由NaN)通过将自回归模型拟合到间隙周围的样本并从两个方向外推至间隙中。
tTrueSignal = (0:199)/199;
xTrueSignal = exp(-.5*tTrueSignal).*sin(2*pi*5*tTrueSignal);
gapSignal = xTrueSignal;
gapSignal(50:140) = NaN;
y = fillgaps(gapSignal);
plot(tTrueSignal,xTrueSignal,'-', ...
tTrueSignal,gapSignal,'o', ...
tTrueSignal,y,'.')
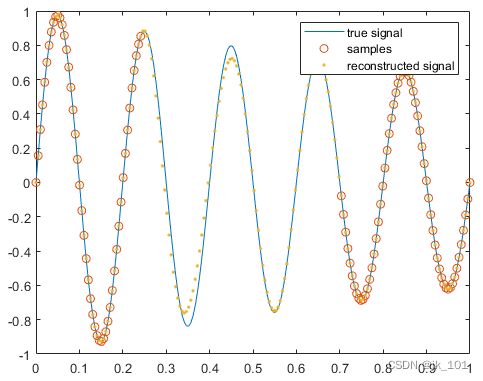
legend('true signal','samples','reconstructed signal')如图所示:
这项技术之所以有效,是因为自回归信号的信息分散在许多样本中。只需要任何片段中的几个样本来完全重建完整的信号。
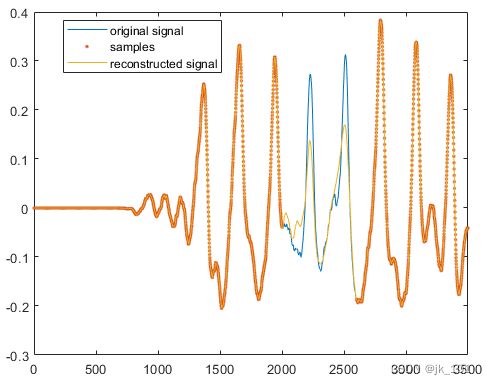
这种类型的重建可以适用于估计更复杂信号的丢失样本。考虑在弹拨后立即移除600个样本后弹拨的吉他弦的采样音频信号:
[y,fs] = audioread('guitartune.wav');
x = y(1:3500);
x(2000:2600) = NaN;
y2 = fillgaps(x);
plot(1:3500, y(1:3500), '-', ...
1:3500, x, '.', ...
1:3500, y2, '-')
legend('original signal','samples','reconstructed signal',...
'Location','best')如图所示:
用局部估计重建间隙
当已知间隙附近的信号可以用单个自回归过程建模时,在间隙内填充数据是相当简单的。当信号由非恒定自回归过程组成时,可以通过限制计算模型参数的区域来缓解问题。当试图填补一个共振的“振铃”期内的间隙时,这是很有用的,该共振紧接在另一个更强的共振之前或之后。
x = y(350001:370000);
x(6000:6950) = NaN;
y2 = fillgaps(x);
y3 = fillgaps(x,1500);
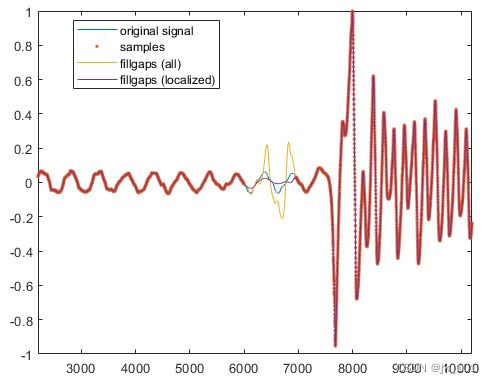
plot(1:20000, y(350001:370000), '-', ...
1:20000, x, '.', ...
1:20000, y2, '-', ...
1:20000, y3, '-')
xlim([2200 10200])
legend('original signal','samples','fillgaps (all)','fillgaps (localized)',...
'Location','best')如图所示:
在上面的图中,波形在一个大共振之前丢失了一个部分。和以前一样,fillgaps用于使用所有可用数据外推至间隙区域。第二次打电话给fillgaps仅使用间隙两侧的1500个样本来执行建模。这减轻了样本7500之后的后续吉他弹拨的影响。
摘要
已经看到了使用插值、重采样和自回归建模从相邻样本值重建缺失数据的几种方法。
插值和重采样适用于缓慢变化的信号。使用抗混叠滤波器进行重采样通常可以更好地重构由低频成分组成的信号。对于重建振荡信号中的大间隙,间隙附近的自回归建模可能特别有效。