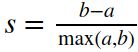[人工智能-综述-10]：模型评估 - 常见的模型评估指标与方法大全、汇总

作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/124238930

---

目录

前言：

第1章 模型评估概述

1.1 什么是模型评估

1.2 模型评估的类型

1.3 过拟合、欠拟合

1.4 模型泛化能力

第2章 常见的分类模型评估指标

2.1 混淆矩阵：

2.4 召回率recall：

2.5 F1-score：主要用于评估模型的稳健性

2.6 AUC指标：主要用于评估样本不均衡的情况

2.7 AUC

2.8 PR曲线

第3章 常见的回归模型评估指标（容易理解）

3.1 向量的距离

3.2 平均绝对误差（MAE）

3.3 平均平方误差（MSE）

3.4 均方根误差（RMSE）

3.5 解释变异

3.6 决定系数

第4章 常见的聚类模型评估指标

4.1 兰德指数

4.2 互信息

4.3 轮廓系数

---

前言：

简单的讲，模型评估就是评估训练好的模型的好坏。

本文主要目的是汇总常见的各种指标。

至于每个指标的含义以及各自的代码示例，将在后续的章节详解介绍。

第1章 模型评估概述

1.1 什么是模型评估

模型评估是对训练好的模型性能进行评估, 模型评估是模型开发过程不可或缺的一部分。它有助于发现表达数据的最佳模型和所选模型将来工作的性能如何。

1.2 模型评估的类型

 机器学习的任务有回归,分类和聚类，针对不同的任务有不同的评价指标。按照数据集的目标值不同，可以把模型评估分为分类模型评估和回归模型评估。

1.3 过拟合、欠拟合

（1）欠拟合

 欠拟合（或称：拟合不足、欠配，英文：underfitting）是指模型在训练数据上没有获得充分小的误差．造成欠拟合的原因通常是模型学习能力过低，具体地说，就是模型参数过少或者结构过于简单，以至于无法学习到数据的内在结构和特征．例如，当用一个线性模型去拟合非线性数据时，会发生欠拟合．由此，可以通过增加模型参数和复杂度，提高学习能力，从而解决欠拟合问题．与欠拟合相对应的，是过度拟合．

（2） 过拟合

是指为了得到一致假设而使假设变得过度严格。

避免过拟合是分类器设计中的一个核心任务。

通常采用增大数据量和测试样本集的方法对分类器性能进行评价。

无论是欠拟合还是过拟合，都是模型泛化能力差的表现。 

1.4 模型泛化能力

泛化能力（generalization ability）是指机器学习算法对新鲜样本的适应能力。 

机器学习的目的是学到隐含在数据背后的规律，对具有同一规律的学习集以外的数据，经过训练的网络也能给出合适的输出，该能力称为泛化能力。

规律适用于现有数据，同样也适用于新鲜数据。

第2章 常见的分类模型评估指标

2.1 混淆矩阵：

混淆矩阵是监督学习中的一种可视化工具，主要用于模型的分类结果和实例的真实信息的比较 。

矩阵中的每一行代表实例的预测类别，每一列代表实例的真实类别。

2.2 准确率Accuracy：

准确率是最常用的分类性能指标。

Accuracy = (TP+TN)/(TP+FN+FP+TN)

预测正确的数占样本总数的比例，即正确预测的正反例数 /总数。

2.3 精确率（Precision）：

精确率容易和准确率被混为一谈。

其实，精确率只是针对预测正确的正样本而不是所有预测正确的样本。

表现为预测出是正的里面有多少真正是正的。可理解为查准率。

Precision = TP/(TP+FP)

即正确预测的正例数 /预测正例总数

2.4 召回率recall：

召回率表现出在实际正样本中，分类器能预测出多少。

与真正率相等，可理解为查全率。正确预测为正占全部正校本的比例

Recall = TP/(TP+FN)，即正确预测的正例数 /实际正例总数

2.5 F1-score：主要用于评估模型的稳健性

F值是精确率和召回率的调和值，更接近于两个数较小的那个，所以精确率和召回率接近时，F值最大。很多推荐系统的评测指标就是用F值的。

2/F1 = 1/Precision + 1/Recall

2.6 AUC指标：主要用于评估样本不均衡的情况

逻辑回归里面，对于正负例的界定，通常会设一个阈值，大于阈值的为正类，小于阈值为负类。如果我们减小这个阀值，更多的样本会被识别为正类，提高正类的识别率，但同时也会使得更多的负类被错误识别为正类。为了直观表示这一现象，引入ROC。根据分类结果计算得到ROC空间中相应的点，连接这些点就形成ROC curve，横坐标为False Positive Rate(FPR假正率)，纵坐标为True Positive Rate(TPR真正率)。一般情况下，这个曲线都应该处于(0,0)和(1,1)连线的上方,如图：

2.7 AUC

AUC（Area Under Curve）被定义为ROC曲线下的面积(ROC的积分)，通常大于0.5小于1。随机挑选一个正样本以及一个负样本，分类器判定正样本的值高于负样本的概率就是 AUC 值。AUC值(面积)越大的分类器，性能越好，如图

2.8 PR曲线

PR曲线的横坐标是精确率P，纵坐标是召回率R。评价标准和ROC一样，先看平滑不平滑（蓝线明显好些）。一般来说，在同一测试集，上面的比下面的好（绿线比红线好）。当P和R的值接近时，F1值最大，此时画连接(0,0)和(1,1)的线，线和PRC重合的地方的F1是这条线最大的F1（光滑的情况下），此时的F1对于PRC就好像AUC对于ROC一样。一个数字比一条线更方便调型。

第3章 常见的回归模型评估指标（容易理解）

拟合（回归）问题比较简单，所用到的衡量指标也相对直观。

假设yiyi是第ii个样本的真实值，ŷ iy^i是对第ii个样本的预测值。

3.1 向量的距离

（1）欧式距离/几何距离

 欧几里得度量（euclidean metric）（也称欧氏距离）是一个通常采用的距离定义，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。

在二维和三维空间中的欧氏距离就是两点之间的实际距离。

（2）曼哈顿距离

出租车几何或曼哈顿距离（Manhattan Distance）是由十九世纪的赫尔曼·闵可夫斯基所创词汇 ，是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。

图1中红线代表曼哈顿距离，绿色代表欧氏距离，也就是直线距离，而蓝色和黄色代表等价的曼哈顿距离。曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离，即d(i,j)=|xi-xj|+|yi-yj|。对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离，因此，曼哈顿距离又称为出租车距离（出租车在两点之间的行驶距离）

（2）马氏距离

马哈拉诺比斯距离 Mahalanobis Distance，简称马氏距离，是在规范化的主成分空间中的欧氏距离。所谓规范化的主成分空间就是利用主成分分析对一些数据进行主成分分解。再对所有主成分分解轴做归一化，形成新的坐标轴。由这些坐标轴张成的空间就是规范化的主成分空间。

马氏距离(Mahalanobis Distance)是一种距离的度量，可以看作是欧氏距离的一种修正，修正了欧式距离中各个维度尺度不一致且相关的问题。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系（例如：一条关于身高的信息会带来一条关于体重的信息，因为两者是有关联的）并且是尺度无关的（scale-invariant），即独立于测量尺度。
 

（3）余弦距离

余弦距离（也称为余弦相似度）： 用向量空间中两个向量夹角的余弦值 作为衡量两个个体
间差异的大小的度量。

向量：多维空间中有方向的线段，如果两个向量的方向一致，即夹角接近零，那么这两个向量就相近 。而要确定两个向量方向是否一致，这就要用到余弦定理计算向量的夹角。

当两个向量是正交（垂直）时，无论其物理距离有多近，其余弦距离始终为最大值cos90°=0.

3.2 平均绝对误差（MAE）

 平均绝对误差MAE（Mean Absolute Error）又被称为l1范数损失（l1-norm loss）：

3.3 平均平方误差（MSE）

平均平方误差MSE（Mean Squared Error）又被称为l2范数损失（l2-norm loss）：

3.4 均方根误差（RMSE）

RMSE虽然广为使用，但是其存在一些缺点，因为它是使用平均误差，而平均值对异常点（outliers）较敏感，如果回归器对某个点的回归值很不理性，那么它的误差则较大，从而会对RMSE的值有较大影响，即平均值是非鲁棒的。

 

3.5 解释变异

解释变异（ Explained variance）是根据误差的方差计算得到的：

3.6 决定系数

决定系数（Coefficient of determination）又被称为R2。

第4章 常见的聚类模型评估指标

4.1 兰德指数

兰德指数（Rand index）需要给定实际类别信息C，假设K是聚类结果，a表示在C与K中都是同类别的元素对数，b表示在C与K中都是不同类别的元素对数，则兰德指数为：

其中数据集中可以组成的总元素对数，RI取值范围为[0,1]，值越大意味着聚类结果与真实情况越吻合。

对于随机结果，RI并不能保证分数接近零。为了实现“在聚类结果随机产生的情况下，指标应该接近零”，调整兰德系数（Adjusted rand index）被提出，它具有更高的区分度：

具体计算方式参见Adjusted Rand index。

ARI取值范围为[−1,1]，值越大意味着聚类结果与真实情况越吻合。从广义的角度来讲，ARI衡量的是两个数据分布的吻合程度。

4.2 互信息

互信息（Mutual Information）也是用来衡量两个数据分布的吻合程度。假设UU与VV是对NN个样本标签的分配情况，则两种分布的熵（熵表示的是不确定程度）分别为：

利用基于互信息的方法来衡量聚类效果需要实际类别信息，MI与NMI取值范围为[0,1]，AMI取值范围为[−1,1]，它们都是值越大意味着聚类结果与真实情况越吻合。

4.3 轮廓系数

轮廓系数（Silhouette coefficient）适用于实际类别信息未知的情况。对于单个样本，设aa是与它同类别中其他样本的平均距离，bb是与它距离最近不同类别中样本的平均距离，轮廓系数为：

对于一个样本集合，它的轮廓系数是所有样本轮廓系数的平均值。

轮廓系数取值范围是[−1,1]

---

作者主页(文火冰糖的硅基工坊)：文火冰糖（王文兵）的博客_文火冰糖的硅基工坊_CSDN博客

本文网址：https://blog.csdn.net/HiWangWenBing/article/details/124238930