机器学习 mean shift聚类算法

Mean Shift介绍

Mean Shift (均值漂移)是基于密度的非参数聚类算法,其算法思想是假设不同簇类的数据集符合不同的概率密度分布,找到任一样本点密度增大的最快方向(最快方向的含义就是Mean Shift) ,样本密度高的区域对应于该分布的最大值,这些样本点最终会在局部密度最大值收敛,且收敛到相同局部最大值的点被认为是同一簇类的成员。

Mean Shift的原理

均值漂移聚类的目的是发现一个平滑密度的样本点。它是一种基于质心的算法，其工作原理是将质心的候选点更新为给定区域内的点的平均值。然后在后处理阶段对这些候选点进行过滤，以消除近似重复点，形成最终的一组质心。给定一个候选质心xi和迭代次数t，按照以下的等式进行更新:

$$x_i^{t+1}=m\left(x_i^t\right)$$
其中N(xi)是在xi周围给定距离内的样本的邻域，m是针对指向点密度最大增长区域的每个质心计算的平均位移向量。使用以下公式进行计算，能有效地更新一个质心为其邻域内样本的平均值:

$$m\left(x_i\right)=\frac{{\sum }_{x_{j\in N}\left(x_i\right)}K\left(x_j-x_i\right)x_j}{{\sum }_{x_j\in N\left(x_i\right)}K\left(x_j-x_i\right)}$$
Mean Shift算法的流程可被理解为：

1. 计算每个样本的平均位移
   

2. 对每个样本点进行平移
   

3. 重复（1）（2），直到样本收敛
   

4. 收敛到相同点的样本可被认为是同一簇类的成员
   

Mean Shift算法的优缺点

不需要设置簇的个数也可以处理任意形状的簇类，同时算法需要的参数较少，且结果较为稳定不需要像K-means的样本初始化。但同时Mean Shift对于较大的特征空间需要的计算量非常大，而且如果参数设置的不好则会较大的影响结果，如果bandwidth设置的太小收敛太慢，而如果bandwidth参数设置的过大，一部分簇则会丢失。

# 导入相关模块和导入数据集
import numpy as np
from sklearn.cluster import MeanShift, estimate_bandwidth
from sklearn.datasets import make_blobs
# 生成样本数据
centers = [[1, 1], [-1, -1], [1, -1]]
X, _ = make_blobs(n_samples=10000, centers=centers, cluster_std=0.6)
es_bandwidth = estimate_bandwidth(X,quantile=0.2, n_samples= 500)
'''
estimate_bandwidth()用于生成mean-shift窗口的尺寸，
其参数的意义为：从X中随机选取500个样本，
计算每一对样本的距离，然后选取这些距离的0.2分位数作为返回值
'''
MS = MeanShift(bandwidth=es_bandwidth)
MS.fit(X)
labels = MS.labels_
cluster_centers = MS.cluster_centers_
uni_labels = np.unique(labels)
n_clusters_ = len(uni_labels)
import matplotlib.pyplot as plt
from itertools import cycle
# 对算法聚类结果进行可视化
colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')
for k, col in zip(range(n_clusters_), colors):
    my_members = labels == k
    cluster_center = cluster_centers[k]
    plt.plot(X[my_members, 0], X[my_members, 1], col + '.')
    plt.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
             markeredgecolor='k', markersize=14)
plt.show()

结果：

from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA
from sklearn.preprocessing import scale
from sklearn.datasets import load_iris  
iris = load_iris()
 
 
data = scale(iris.data)
reduced_data = data#PCA(n_components=3).fit_transform(data)
MS = MeanShift(bandwidth = 1.4)
MS.fit(reduced_data)
label_pred = MS.labels_
n_digits = len(np.unique(MS.labels_))

 
plt.clf()
# 画簇心和点
plt.figure(figsize = (10,7))
centroids = MS.cluster_centers_
plt.plot(centroids[:, 0], centroids[:, 1],'o', markerfacecolor=col,markeredgecolor='k', markersize=14)
color_list=[ 'r', 'b','g', 'b', '#800080',
             '#CD5C5C', '#DAA520', '#E6E6FA', '#F08080', '#FFE4C4']
for i in range(n_digits):
    x = reduced_data[label_pred == i]
    plt.scatter(x[:, 0], x[:, 1], c=color_list[i], marker='.', label='label%s'%i)
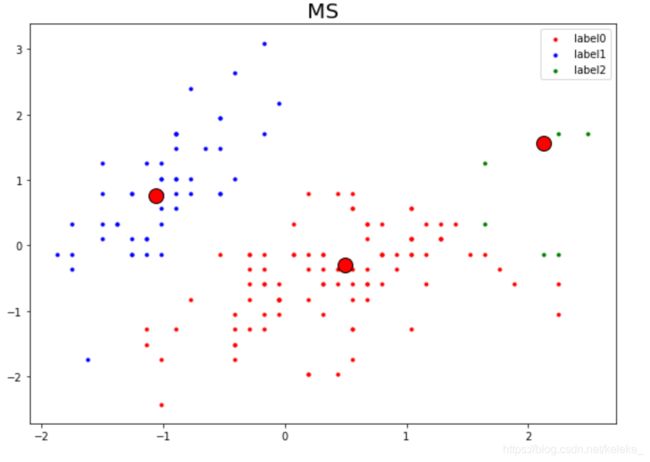
plt.title('MS',size = 20)
plt.legend()
plt.axis('on')
plt.show()

结果：