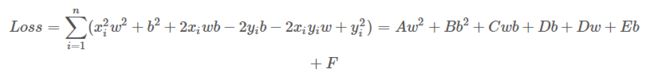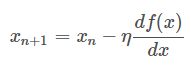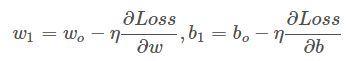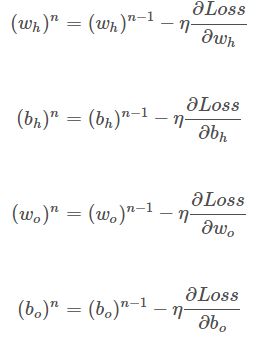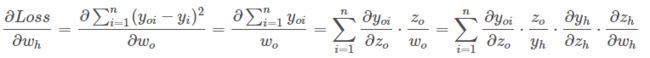Datawhale《深度学习-NLP》Task5- 神经网络基础

 

基本概念

前馈神经网络，网络层数，输入层，隐藏层，输出层，隐藏单元，激活函数

前馈神经网络（Feedforward Neural Network）

网络结构(一般分两种)

1. Back Propagation Networks - 反向传播网络

2. RBF networks - 径向基函数神经网络

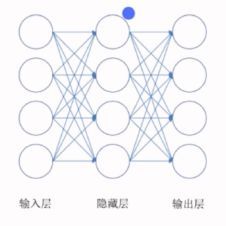
BP网络是所有的神经网络中结构最为简单的一种网络。一般我们习惯把网络画成左边输入右边输出层的结构。

一个向量从输入层进入，经过网络作用，在输出层产生输出结果。BP神经网络的网络结构是不固定的。

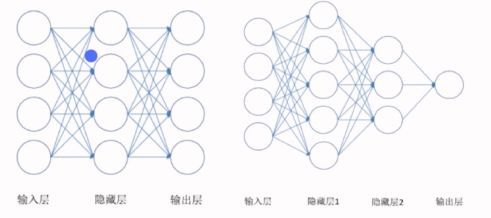
第二个神经网络有三层，两个隐藏层。

前馈神经网络，不要求对称，在不同的网络结构下产生不同的训练效果和运行特点。

最简单的BP网络：

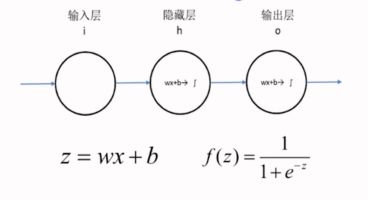
总共有两层，有一个隐藏层和一个输出层，一共两层。从第二层开始算一层。

输入x最简单化，x一维是一个实数。隐藏层h和输出层o结构。

由这两个函数所组成。一旦这里输入x,y之后就可以开始训练了。

网络结构

前馈神经网络的结构不固定，一般神经网络包括输入层、隐层和输出层，下面的图一的神经网络由两层，每层4个节点。第二个神经网络有两个隐层，第一层5个节点，第二层3个节点，最后一层输出层只有一个节点。神经网络有很多种设计模式，并在不同的模式下产生不同的效果。

神经网络的复杂之处在于他的组成结构爱太复杂，神经元太多，为了方便简介，我们设计一个最简单的BP网络结构，如下图所示。

这是一个只有两层的神经网络，x我们也让他最简化，就一个实数，我们规定隐层h和输出层o这两层都是$z=wx+b$和$f(z)=\frac{1}{1+e^{-z}}$的组合，一旦输入样本x和标签y之后，模型就开始训练了。那么我们的问题就变成了求隐层的w、b和输出层的w、b四个参数的过程。
 

开始训练

　　我们想要得到中的w和b，我们有众多的样本x和标签y，在这里写作y和x的关系，假设拟合的过程中有这样的一个参数代表error，表示误差的意思，

当我们有n对x和y那么就有n个$e$，我们试着把n个$e$都加起来表示一个误差总量，为了不让残差正负抵消我们取平方或者取绝对值，本文取平方。这种误差我们称为“残差”，也就是我们建模之后进行拟合出的结果和真实结果之间的差值。损失函数Loss还有一种称呼叫做“代价函数Cost”，

现在我们要做的就是找到一个比较好的w和b，使得整个Loss尽可能的小，越小说明我们训练出来的模型越好。

梯度下降法

　　老规矩，求最小值我们一般中梯度下降算法，通过迭代不断的优化待定系数w和b。我们的残差到底是一个怎样的函数呢，他的图形到底长什么样子呢？到底该怎么求他的最小值呢？OK,为了方便读者理解，我把Loss函数给你们画出来。

我们初始化一个$w_o$和$b_0$，带到Loss里面去，这个点($w_o,b_o,Loss_o$)会出现在碗壁的某个位置，而我们的目标位置是碗底，那就慢慢的一点一点的往底部挪吧。

$\eta$是学习率，也就是每次挪动的步长，$\eta$大每次迭代的脚步就大，$\eta$小每次迭代的脚步就小，我们只有取到合适的$\eta$才能尽可能的接近最小值而不会因为步子太大越过了最小值。到后面每次移动的水平距离实在逐步减小的，原因就是因为整个函数圆乎乎的底部斜率在降低，吃个栗子：

 

如图所示，当$x_n=3$时，$-\eta\frac{f(x)}{dx}$为负数，更新后$x_{n+1}$会减小；当$x_n=-3$时，$-\eta\frac{f(x)}{dx}$为正数，更新后$x_{n+1}$还是会减小。这总函数其实就是凸函数。满足$f(\frac{x_i+x_2}{2})=\frac{f(x_i)+f(x_2)}{2}$都是凸函数。沿着梯度的方向是下降最快的。
-我们初始化$(w_0,b_0,Loss_o)$后下一步就水到渠成了，

有了梯度和学习率的$\eta$乘积之后，当这个点逐渐接近“碗底”的时候，偏导也随之下降，移动步伐也会慢慢变小，收敛会更为平缓，不会轻易出现“步子太大”而越过最低的情况。一轮一轮迭代，直到每次更新的值非常小，损失值不在减小就可以判断为训练结束，此时得到的(w,b)就是我们要求的模型。

神经网络的训练

　　哈哈哈，是不是发现我刚才讲的明明是线性回归模型的训练，和大家想知道的神经网络的训练有毛线关系呀！你们说的没错，就是有一毛钱的关系，嘿嘿[笑脸]！

这个网络用函数表达式写的话如下所示：

第一层(隐藏层)　　$

第二层(输出层)　

接下来的工作就是把$w_h、b_h、w_o、b_o$参数利用梯度下降算法求出来，把损失函数降低到最小，那么我们的模型就训练出来呢。

第一步：准备样本，每一个样本$x_i$对应标签$y_i$。

第二步：清洗数据，清洗数据的目的是为了帮助网络更高效、更准确地做好分类。

第三步：开始训练，

$Loss=\sum_{i=1}^{n}(y_{oi}-y_i)^2$

我们用这四个表达式，来更新参数。

问题来了，$\frac{\partial Loss}{\partial w_h}$、$\frac{\partial Loss}{\partial b_h}$、$\frac{\partial Loss}{\partial w_o}$、$\frac{\partial Loss}{\partial b_o}$这4个值怎么求呢？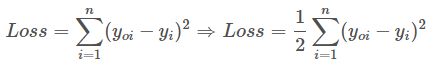

配一个$\frac{1}{2}$出来，为了后面方便化简。

其他三个参数，和上面类似，这是一种“练乘型”求导方式。我们的网络两层就4个连乘，如果是10层，那么就是20个连乘。但一层网络的其中一个节点连接着下一层的其他节点时，那么这个节点上的系数的偏导就会通过多个路径传播过去，从而形成“嵌套型关系”。

 

DropOut

　　DropOut是深度学习中常用的方法，主要是为了克服过拟合的现象。全连接网络极高的VC维，使得它的记忆能力非常强，甚至把一下无关紧要的细枝末节都记住，一来使得网络的参数过多过大，二来这样训练出来的模型容易过拟合。

　　DropOut：是指在在一轮训练阶段临时关闭一部分网络节点。让这些关闭的节点相当去去掉。如下图所示去掉虚线圆和虚线，原则上是去掉的神经元是随机的。

 

Tensorflow实现基本的神经网络

其实是从一个层到10层再到10层的这样的一个神经网络。

解析
初始的输入的矩阵为：[[1],300个,[-1]] 大致这样的
在增加一层的那个函数中，最为经典的地方是，偏置（biases）的第一个维度必须选为1。看下面推理。
第一部分：
输入为：(300*1)的矩阵，之后，经过了第一个层，就是(300 * 1)* (1*10) + (1, 10)。这显然是合理的，每一层的数据，到神经网络中的中间层的每一个节点上，然后每个节点上都加一个偏置biases。
就是在每个上都同时加，通过下面的例子就可以看出来。

>>> import numpy as np
>>> a = np.random.normal(0, 1, (2, 4))
>>> a
array([[-0.60675395, -0.06779251,  1.50473051, -0.82511157],
       [ 1.14550373,  0.372316  ,  0.45110457, -0.41554109]])
>>> b = np.random.normal(0, 1, (1, 4))
>>> b
array([[ 0.48946834, -0.70514578,  2.12102107, -0.25960606]])
>>> a + b
array([[-0.11728561, -0.77293828,  3.62575157, -1.08471763],
       [ 1.63497208, -0.33282978,  2.57212564, -0.67514715]])
>>>

• 第二部分:
• 输出的内容为上面的输出：（300*10）的矩阵。
• 进行的计算为：(300 * 10) * (10 * 1) + (1, 1) 后面的那个为偏置，每个都加上了这样的一个偏置。

经过上面的推理，我们就可以理解了为什么中间添加新的一层的时候，需要将biases的第一次参数为1

• 发现写tensorflow就想当于写数学公式一样，怪不得TensorFlow在研究数学的老师那边那么容易上手 hh

代码

import tensorflow as tf
import numpy as np

# TensorFlow嫌弃了我这台电脑的CPU(我这就避免了警报)
# ==================
import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
# ==================

# 创建一些等距离的数据(数据量为300)，同时用np.newaxis进行扩展一个维度
x_data = np.linspace(-1, 1, 300, dtype=np.float32)[:, np.newaxis]
# 创建同等规模的噪音(这里采用的是均值为0,标准差为0.05的,保持shape和类型一致)
noise = np.random.normal(0, 0.05, x_data.shape).astype(np.float32)
# 原数据label(y = x^2 - 0.5) 之后添加一点点噪声(让人感觉更像现实中获取的数据一样)
y_data = np.square(x_data) - 0.5 + noise


# 创建一个添加层数的函数,使得实现变得简单
# inputs是输出的东西，in_size表示的是该层的输入层维度，out_size表示的是该层的输出层维度，activation_function就是一个
def add_layer(inputs, in_size, out_size, activation_function=None):
    # 创建系数矩阵，矩阵规模为 [in_size * out_size]
    Weights = tf.Variable(tf.random_normal([in_size, out_size]))
    # 创建一个biases矩阵，这里考虑到biases用0不是那么好，所以，一开始设置的时候加个0.1
    biases = tf.Variable(tf.zeros([1, out_size]) + 0.1)
    # 构建方程
    Wx_plus_b = tf.matmul(inputs, Weights) + biases

    if activation_function == None:
        output = Wx_plus_b
    else:
        output = activation_function(Wx_plus_b)
    return output


xs = tf.placeholder(tf.float32, [None, 1])
ys = tf.placeholder(tf.float32, [None, 1])
# 得到中间那一层
l1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu)
# 得到输出层
prediction = add_layer(l1, 10, 1)
# 在300个求一个平方和的均值，设置了切片的index为1，原因是最后的矩阵规模为300*1，大致类似:[[1],300个,[2]]
loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction),
                                    reduction_indices=[1]))
# 梯度下降训练
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)
# 变量初始化
init = tf.global_variables_initializer()
# 启动会话
with tf.Session() as sess:
    sess.run(init)
    for i in range(1000):
        # training
        sess.run(train_step, feed_dict={xs: x_data, ys: y_data})
        if i % 50 == 0:
            # to see the step improvement
            print(sess.run(loss, feed_dict={xs: x_data, ys: y_data}))

附上有图形演示的代码

由于不同起始数据，画出几个不同的结果。下面列举其中的两个

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
# TensorFlow嫌弃了我这台电脑的CPU(我这就避免了警报)
# ==================
import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
# ==================

# 创建一些等距离的数据(数据量为300)，同时用np.newaxis进行扩展一个维度
x_data = np.linspace(-1, 1, 300, dtype=np.float32)[:, np.newaxis]
# 创建同等规模的噪音(这里采用的是均值为0,标准差为0.05的,保持shape和类型一致)
noise = np.random.normal(0, 0.05, x_data.shape).astype(np.float32)
# 原数据label(y = x^2 - 0.5) 之后添加一点点噪声(让人感觉更像现实中获取的数据一样)
y_data = np.square(x_data) - 0.5 + noise


# 创建一个添加层数的函数,使得实现变得简单
# inputs是输出的东西，in_size表示的是该层的输入层维度，out_size表示的是该层的输出层维度，activation_function就是一个
def add_layer(inputs, in_size, out_size, activation_function=None):
    # 创建系数矩阵，矩阵规模为 [in_size * out_size]
    Weights = tf.Variable(tf.random_normal([in_size, out_size]))
    # 创建一个biases矩阵，这里考虑到biases用0不是那么好，所以，一开始设置的时候加个0.1
    biases = tf.Variable(tf.zeros([1, out_size]) + 0.1)
    # 构建方程
    Wx_plus_b = tf.matmul(inputs, Weights) + biases

    if activation_function == None:
        output = Wx_plus_b
    else:
        output = activation_function(Wx_plus_b)
    return output


xs = tf.placeholder(tf.float32, [None, 1])
ys = tf.placeholder(tf.float32, [None, 1])
# 得到中间那一层
l1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu)
# 得到输出层
prediction = add_layer(l1, 10, 1)
# 在300个求一个平方和的均值，设置了切片的index为1，原因是最后的矩阵规模为300*1，大致类似:[[1],300个,[2]]
loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction),
                                    reduction_indices=[1]))
# 梯度下降训练
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)
# 变量初始化
init = tf.global_variables_initializer()
# 启动会话
with tf.Session() as sess:
    sess.run(init)
    fig = plt.figure()
    # 创建两个子图
    ax_begin = fig.add_subplot(2, 1, 1)
    ax_end = fig.add_subplot(2, 1, 2)
    ax_begin.scatter(x_data, y_data)
    ax_end.scatter(x_data, y_data)

    # 起始版
    prediction_value = sess.run(prediction, feed_dict={xs: x_data})
    # plot the prediction
    ax_begin.plot(x_data, prediction_value, 'r-', lw=5)
    ax_begin.set_title("Begin")
    plt.tight_layout()

    for i in range(1000):
        # training
        sess.run(train_step, feed_dict={xs: x_data, ys: y_data})
        if i % 50 == 0:
            # to see the step improvement
            print(sess.run(loss, feed_dict={xs: x_data, ys: y_data}))

    # 经过迭代后的版本
    prediction_value = sess.run(prediction, feed_dict={xs: x_data})
    # plot the prediction
    ax_end.plot(x_data, prediction_value, 'r-', lw=5)
    ax_end.set_title("End")
    plt.show()

 

激活函数

激活函数的性质

非线性： 当激活函数是线性的时候，一个两层的神经网络就可以逼近基本上所有的函数了。但是，如果激活函数是恒等激活函数的时候（即），就不满足这个性质了，而且如果MLP使用的是恒等激活函数，那么其实整个网络跟单层神经网络是等价的。
可微性： 当优化方法是基于梯度的时候，这个性质是必须的。
单调性： 当激活函数是单调的时候，单层网络能够保证是凸函数
 

为什么要用激活函数？

神经网络中激活函数的主要作用是提供网络的非线性建模能力，如不特别说明，激活函数一般而言是非线性函数。假设一个示例神经网络中仅包含线性卷积和全连接运算，那么该网络仅能够表达线性映射，即便增加网络的深度也依旧还是线性映射，难以有效建模实际环境中非线性分布的数据。加入（非线性）激活函数之后，深度神经网络才具备了分层的非线性映射学习能力。因此，激活函数是深度神经网络中不可或缺的部分。

激活函数可以帮助神经网络隔离噪声点。即激活有用的信息，抑制无关的数据点。
 

激活函数种类

sigmod函数

Sigmoid 是使用范围最广的一类激活函数，具有指数函数形状 。正式定义为：

函数对应图像为：

优点：

•  sigmoid函数的输出映射在(0,1)之间，单调连续，输出范围有限，优化稳定，可以用于输入的归一化，也可以用作输出层。
•  求导容易

缺点：

•  由于其软饱和性，即容易产生梯度消失，导致训练出现问题。
•  其输出并不是以0为中心的

说明：

饱和性可以分为软饱和、硬饱和。其中，软饱和是指函数的导数趋近于0，硬饱和是指函数的导数等于0。

Sigmoid 的软饱和性，使得深度神经网络在二三十年里一直难以有效的训练，是阻碍神经网络发展的重要原因。具体来说，由于在后向传递过程中，sigmoid向下传导的梯度包含了一个f'(x) 因子（sigmoid关于输入的导数），因此一旦输入落入饱和区，f'(x) 就会变得接近于0，导致了向底层传递的梯度也变得非常小。此时，网络参数很难得到有效训练。这种现象被称为梯度消失。一般来说， sigmoid 网络在 5 层之内就会产生梯度消失现象[2]。梯度消失问题至今仍然存在，但被新的优化方法有效缓解了，例如DBN中的分层预训练，Batch Normalization的逐层归一化，Xavier和MSRA权重初始化等代表性技术。

Sigmoid 的饱和性虽然会导致梯度消失，但也有其有利的一面。例如它在物理意义上最为接近生物神经元。 (0, 1) 的输出还可以被表示作概率，或用于输入的归一化，代表性的如Sigmoid交叉熵损失函数

sigmoid的输出均大于0，使得输出不是0均值，称为偏移现象，这将导致后一层的神经元将上一层输出的非0均值的信号作为输入。关于原点对称的输入和中心对称的输出，网络会收敛地更好。
 

tanh函数

tanh的公式如下：

函数对应的图像如下：

优点：

 比sigmoid函数收敛速度更快。
 相比sigmoid函数，其输出以0为中心。
缺点：

 依旧具有软饱和问题。
说明：

Xavier在文献[2]中分析了sigmoid与tanh的饱和现象及特点，具体见原论文。此外，文献 [3] 中提到tanh 网络的收敛速度要比sigmoid快。因为 tanh 的输出均值比 sigmoid 更接近 0，SGD会更接近 natural gradient[4]（一种二次优化技术），从而降低所需的迭代次数。

ReLU函数

Relu的公式如下：

函数对应的图像如下：

优点：

•  Relu具有线性、非饱和的特点，并且相比Sigmoid和tanh，Relu的收敛速度更快。
•  Relu实现比较简单。
•  Relu有效缓解了梯度下降问题。
•  提供了神经网络的稀疏表达能力

缺点：

•  随着训练的进行，可能会出现神经元死亡，权重无法更新的情况。
•  当x<0时，Relu是硬饱和的。

说明：

ReLU是一种后来才出现的激活函数。从图中可以看到，当x<0时，出现硬饱和，当x>0时，不存在饱和问题。因此，ReLU 能
够在x>0时保持梯度不衰减，从而缓解梯度消失问题。然而，随着训练的推进，部分输入会落入硬饱和区，导致对应权重无法更

新，这种现象被称为“神经元死亡”。

与sigmoid类似，ReLU的输出均值也大于0。偏移现象和神经元死亡会共同影响网络的收敛性。

激活函数大面积没有被激活的原因可能是：1）初始化时，参数的设置使得ReLU没有被激活；2）学习速率太高，神经元在一定范围内波动，可能会发生数据多样性的丢失，这种情况下神经元不会被激活，数据多样性的丢失不可逆转。
 

Leaky-ReLU 与 Parametric -ReLU函数

针对ReLU函数在x<0时的硬饱和问题，出现了Leaky-ReLU与P-ReLU进行改进，它们在形式上相似，不同的是在Leaky-ReLU中，α 是一个常数，实际中必须必须非常小心谨慎地重复训练，从而选取合适的参数a；在P-ReLU中，α 可以作为参数来学习，自适应地从数据中学习参数。PReLU具有收敛速度快、错误率低的特点，可以用于反向传播的训练。

函数图像如下：

 

激活函数选择的建议

1 ) 由于梯度消失问题，有时要避免使用sigmoid和tanh函数

2）ReLU函数基本用在隐藏层。使用 ReLU，一定要小心设置 learning rate，注意不要让你的网络出现很多 “dead” 神经元

3）在人工神经网络（ANN）中，Softmax通常被用作输出层的激活函数。这不仅是因为它的效果好，而且因为它使得ANN的输出值更易于理解。

• softmax函数最明显的特点在于：它把每个神经元的输入占当前层所有神经元输入之和的比值，当作该神经元的输出。这使得输出更容易被解释：神经元的输出值越大，则该神经元对应的类别是真实类别的可能性更高。
• softmax不仅把神经元输出构造成概率分布，而且还起到了归一化的作用，适用于很多需要进行归一化处理的分类问题。
• softmax配合log似然代价函数，其训练效果也要比采用二次代价函数的方式好：二次代价函数在训练ANN时可能会导致训练速度变慢的问题（初始的输出值离真实值越远，训练速度就越慢）。这个问题可以通过采用交叉熵代价函数来解决（当激活函数是sigmod时候），也可以通过softmax的log似然代价函数。
   

深度学习中的正则化

 

回顾过拟合

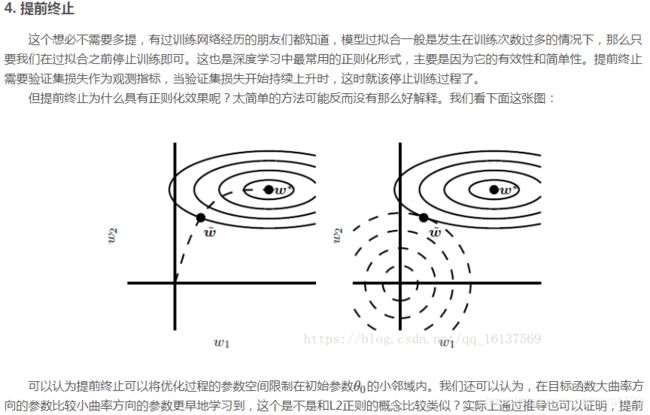
上一篇博客《浅谈机器学习中的过拟合》对过拟合进行了比较详细的分析。过拟合是指学习时选择的模型所包含的参数过多，以至于出现这一模型对已知数据预测的很好，但对未知数据预测的很差的现象。过拟合的是由数据和模型两方面原因共同造成的，最直接防止过拟合的方法是无限增大训练集的大小，让训练集样本与真实数据分布尽可能接近，但这么做实在是不太现实，一是我们根本无从知晓数据真实分布是什么样，二来增加数据集是一个很花费人力物力的而且不能保证效果的方法。所以比较常用的办法是正则化。

什么是正则化

在《Deep Learning》书中定义正则化为“对学习算法的修改——旨在减少泛化误差而不是训练误差”，《统计学习方法》中认为正则化是选择模型的一种方法。我个人比较倾向于后一种解释。在上一篇博客也提到了，模型可以看成是一个高维函数，当模型参数确定了，这个函数也就确定了。对于不同的模型参数，能得到千千万万个不同的模型，我们将这所有的可能得到的模型称之为假设空间。理想情况下，我们希望真实数据的生成过程也包括在这个假设空间中，然后我们只需要通过训练将代表该生成过程的一组模型参数找出来即可。然而，真实数据的生成过程几乎肯定在假设空间之外，我们做的事无非是从已有的假设空间中通过训练找到一个泛化能力优秀的拟合模型（即尽量匹配真实数据生成过程）。正则化可以帮助我们从假设空间中找到这样一个模型：训练误差较低，而且模型复杂度也较小。所以正则化是一种选择模型的方法。 
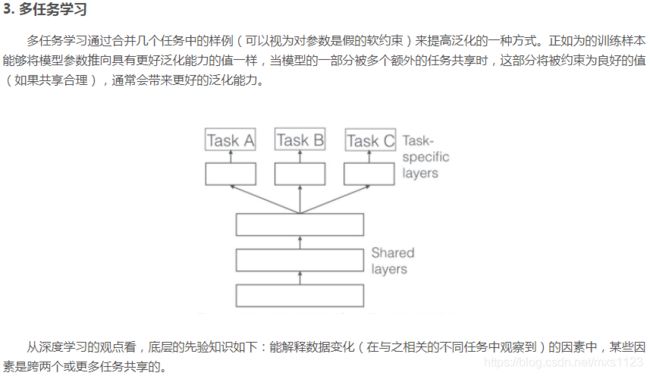
　　正则化的作用是选择经验风险与模型复杂度同时较小的模型。在实际深度学习场景中我们几乎总是会发现，最好的拟合模型（从最小化泛化误差的意义上）是一个适当正则化的大型模型。
 

几种常见的正则化策略

1. 参数范数惩罚

深度模型中的优化

1、学习与纯优化有什么不同

2、神经网络优化中的挑战

3、基本算法

4、自适应学习率算法

5 、优化策略与元算法

Returns:
v -- python dictionary containing the current velocity.
                v['dW' + str(l)] = velocity of dWl
                v['db' + str(l)] = velocity of dbl
"""

L = len(parameters) // 2 # number of layers in the neural networks
v = {}

# Initialize velocity
for l in range(L):
    ### START CODE HERE ### (approx. 2 lines)
    v["dW" + str(l+1)] = np.zeros_like(parameters["W" + str(l+1)])
    v["db" + str(l+1)] = np.zeros_like(parameters["b" + str(l+1)])
    ### END CODE HERE ###

return v

2、更新权值

def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):
"""
Update parameters using Momentum

Arguments:
parameters -- python dictionary containing your parameters:
                parameters['W' + str(l)] = Wl
                parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
                grads['dW' + str(l)] = dWl
                grads['db' + str(l)] = dbl
v -- python dictionary containing the current velocity:
                v['dW' + str(l)] = ...
                v['db' + str(l)] = ...
beta -- the momentum hyperparameter, scalar
learning_rate -- the learning rate, scalar

Returns:
parameters -- python dictionary containing your updated parameters 
v -- python dictionary containing your updated velocities
"""

L = len(parameters) // 2 # number of layers in the neural networks

# Momentum update for each parameter
for l in range(L):

    ### START CODE HERE ### (approx. 4 lines)
    # compute velocities
    v["dW" + str(l+1)] = beta *v["dW" + str(l+1)] +(1-beta)*grads["dW" + str(l+1)]
    v["db" + str(l+1)] = beta *v["db" + str(l+1)] +(1-beta)*grads["db" + str(l+1)]
    # update parameters
    parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * v["dW" + str(l+1)]
    parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * v["db" + str(l+1)]
    ### END CODE HERE ###

return parameters, v

python 实现

def initialize_adam(parameters) :
"""
Initializes v and s as two python dictionaries with:
            - keys: "dW1", "db1", ..., "dWL", "dbL" 
            - values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.

Arguments:
parameters -- python dictionary containing your parameters.
                parameters["W" + str(l)] = Wl
                parameters["b" + str(l)] = bl

Returns: 
v -- python dictionary that will contain the exponentially weighted average of the gradient.
                v["dW" + str(l)] = ...
                v["db" + str(l)] = ...
s -- python dictionary that will contain the exponentially weighted average of the squared gradient.
                s["dW" + str(l)] = ...
                s["db" + str(l)] = ...

"""

L = len(parameters) // 2 # number of layers in the neural networks
v = {}
s = {}

# Initialize v, s. Input: "parameters". Outputs: "v, s".
for l in range(L):
### START CODE HERE ### (approx. 4 lines)
    v["dW" + str(l+1)] = np.zeros_like(parameters['W' + str(l+1)])
    v["db" + str(l+1)] = np.zeros_like(parameters['b' + str(l+1)])
    s["dW" + str(l+1)] = np.zeros_like(parameters['W' + str(l+1)])
    s["db" + str(l+1)] = np.zeros_like(parameters['b' + str(l+1)])
### END CODE HERE ###

return v, s

def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.01, 
beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8): 
“”” 
 

Arguments:
parameters -- python dictionary containing your parameters:
                parameters['W' + str(l)] = Wl
                parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
                grads['dW' + str(l)] = dWl
                grads['db' + str(l)] = dbl
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
learning_rate -- the learning rate, scalar.
beta1 -- Exponential decay hyperparameter for the first moment estimates 
beta2 -- Exponential decay hyperparameter for the second moment estimates 
epsilon -- hyperparameter preventing division by zero in Adam updates

Returns:
parameters -- python dictionary containing your updated parameters 
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
"""

L = len(parameters) // 2                 # number of layers in the neural networks
v_corrected = {}                         # Initializing first moment estimate, python dictionary
s_corrected = {}                         # Initializing second moment estimate, python dictionary

# Perform Adam update on all parameters
for l in range(L):
    # Moving average of the gradients. Inputs: "v, grads, beta1". Output: "v".
    ### START CODE HERE ### (approx. 2 lines)
    v["dW" + str(l+1)] = beta1 * v["dW" + str(l+1)] + (1-beta1) * grads['dW' + str(l+1)]
    v["db" + str(l+1)] = beta1 * v["db" + str(l+1)] + (1-beta1) * grads['db' + str(l+1)]
    ### END CODE HERE ###

    # Compute bias-corrected first moment estimate. Inputs: "v, beta1, t". Output: "v_corrected".
    ### START CODE HERE ### (approx. 2 lines)
    v_corrected["dW" + str(l+1)] = v["dW" + str(l+1)] / (1- np.power(beta1,t))
    v_corrected["db" + str(l+1)] = v["db" + str(l+1)] / (1- np.power(beta1,t))
    ### END CODE HERE ###

    # Moving average of the squared gradients. Inputs: "s, grads, beta2". Output: "s".
    ### START CODE HERE ### (approx. 2 lines)
    s["dW" + str(l+1)] = beta2 * s["dW" + str(l+1)] + (1- beta2) * np.square(grads['dW' + str(l+1)])
    s["db" + str(l+1)] = beta2 * s["db" + str(l+1)] + (1- beta2) * np.square(grads['db' + str(l+1)])
    ### END CODE HERE ###

    # Compute bias-corrected second raw moment estimate. Inputs: "s, beta2, t". Output: "s_corrected".
    ### START CODE HERE ### (approx. 2 lines)
    s_corrected["dW" + str(l+1)] = s["dW" + str(l+1)] / (1-np.power(beta2,t))
    s_corrected["db" + str(l+1)] = s["db" + str(l+1)] / (1-np.power(beta2,t))
    ### END CODE HERE ###

    # Update parameters. Inputs: "parameters, learning_rate, v_corrected, s_corrected, epsilon". Output: "parameters".
    ### START CODE HERE ### (approx. 2 lines)
    parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * v_corrected["dW" + str(l+1)] /np.sqrt(s_corrected["dW" + str(l+1)] +epsilon)
    parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * v_corrected["db" + str(l+1)] /np.sqrt(s_corrected["db" + str(l+1)] +epsilon)
    ### END CODE HERE ###

return parameters, v, s

 

1. https://blog.csdn.net/a19990412/article/details/82919095 

2. https://blog.csdn.net/u010420283/article/details/83754595  （非常好）

3. https://blog.csdn.net/qq_16137569/article/details/81584165 （正则化）

4. https://blog.csdn.net/u012756814/article/details/79995133（深度模型中的优化）

5. https://blog.csdn.net/justpsss/article/details/77680174（深度模型中的优化）