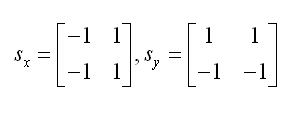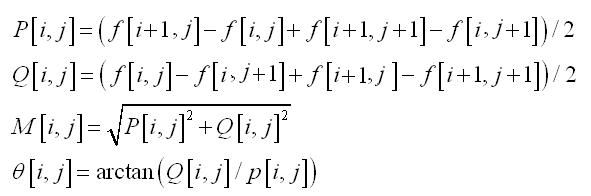几种边缘检测微分算子的比较
预备知识:
梯度------梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值
,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
![]() 该函数就称为函数
该函数就称为函数 ![]() 在点P(x,y)的梯度,记作grad f(x,y)
在点P(x,y)的梯度,记作grad f(x,y)
或![]()
对于图像来说,是一个二维的离散型数集,通过推广二维连续型求函数偏导的方法,来求得图像的偏
导数。
![]()
梯度是一个矢量,则(x,y)处的梯度表示为:![]()
其大小为:![]()
不同图像灰度不同,边界处一般会有明显的边缘,利用此特征可以分割图像。需要说明的是:边缘和物
体间的边界并不等同,边缘指的是图像中像素的值有突变的地方,而物体间的边界指的是现实场景中的存在
于物体之间的边界。有可能有边缘的地方并非边界,也有可能边界的地方并无边缘,因为现实世界中的物体
是三维的,而图像只具有二维信息,从三维到二维的投影成像不可避免的会丢失一部分信息;另外,成像过
程中的光照和噪声也是不可避免的重要因素。正是因为这些原因,基于边缘的图像分割仍然是当前图像研究
中的世界级难题,目前研究者正在试图在边缘提取中加入高层的语义信息。
以像素值为y,以坐标为x(x是二维或者一维),灰度的突变就意味着函数y=f(x)的导数或者高阶导数会
发生突变。因此,我们可以通过检测导数来检测图像的边缘。
在实际中往往只用到一阶和二阶导数,虽然原理上可用更高阶的导数,但因为噪声的影响,在纯粹的二阶导数操作中就会出现对噪声的敏感现象,三阶以上的导数信息往往失去了应用价值。导数操作中就会出现
对噪声的敏感现象,三阶以上的导数信息往往失去了应用价值。二阶导数还可以说明灰度突变的类型。在有
些情况下,如灰度变化均匀的图像,只利用一阶导数可能找不到边界,此时二阶导数就能够提供很有用的信
息。二阶导数对噪声也比较敏感,解决的方法是先对图像进行平滑滤波,消除部分噪声,然后再对处理
后的图像进行边缘检测。不过,利用二阶导数信息的算法是基于过零检测的,因此得到的边缘点数比较少,
有利于后继的处理和识别工作。
各种算子的存在就是对这种导数分割原理进行的实例化计算,是为了在计算过程中直接使用的一种计算
单位。
(1)Roberts算子:边缘定位准,但是对噪声敏感。适用于边缘明显且噪声较少的图像分割。Roberts
边缘检测算子是一种利用局部差分算子寻找边缘的算子,Robert算子图像处理后结果边缘不是很平滑。经分析
,由于Robert算子通常会在图像边缘附近的区域内产生较宽的响应,故采用上述算子检测的边缘图像常需做
细化处理,边缘定位的精度不是很高。
Robert算子是一个2x2算子模板。
![]()
具体使用:
判断f(x,y)是否是边缘点:
![]()
建立一幅二值图像,用于保存边缘检测的结果。如果G(x,y)>T,就将像素值设为1,否则为0。
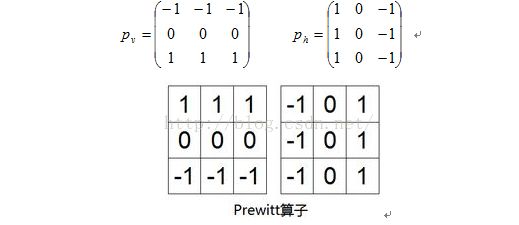
(2)Prewitt算子:对噪声有抑制作用,抑制噪声的原理是通过像素平均,但是像素平均相当于对图像
的低通滤波,所以Prewitt算子对边缘的定位不如Roberts算子。
具体原理和使用:
Pv用于检测水平边缘,Ph用于检测水平边缘。
G(i)=|[f(i-1,j-1)+f(i-1,j)+f(i-1,j+1)]-[f(i+1,j-1)+f(i+1,j)+f(i+1,j+1)]|
G(j)=|[f(i-1,j+1)+f(i,j+1)+f(i+1,j+1)]-[f(i-1,j-1)+f(i,j-1)+f(i+1,j-1)]|
则 P(i,j)=max[G(i),G(j)]或 P(i,j)=G(i)+G(j)
经典Prewitt算子认为:凡灰度新值大于或等于阈值的像素点都是边缘点。即选择适当的阈值T,若P(i,j)
≥T,则(i,j)为边缘点,P(i,j)为边缘图像。P是与原图像同等大小的边缘检测结果。
(3)Sobel算子:Sobel算子和Prewitt算子都是加权平均,但是Sobel算子认为,邻域的像素对当前像素
产生的影响不是等价的,所以距离不同的像素具有不同的权值,对算子结果产生的影响也不同。一般来说,
距离越远,产生的影响越小。抗噪性也比较好。
Sobel算子也有两个,一个是检测垂直边缘的模板(通过计算水平的两个像素值之间的差),另一个是
检测垂直边缘的模板(通过计算垂直的两个像素值之间的差)。
具体计算如下:
Gx = (-1)*f(x-1, y-1) + 0*f(x,y-1) + 1*f(x+1,y-1)
+(-2)*f(x-1,y) + 0*f(x,y)+2*f(x+1,y)
+(-1)*f(x-1,y+1) + 0*f(x,y+1) + 1*f(x+1,y+1)
= [f(x+1,y-1)+2*f(x+1,y)+f(x+1,y+1)]-[f(x-1,y-1)+2*f(x-1,y)
+f(x-1,y+1)]
Gy =1* f(x-1, y-1) + 2*f(x,y-1)+ 1*f(x+1,y-1)
+0*f(x-1,y) 0*f(x,y) + 0*f(x+1,y)
+(-1)*f(x-1,y+1) + (-2)*f(x,y+1) + (-1)*f(x+1, y+1)
= [f(x-1,y-1) + 2f(x,y-1) + f(x+1,y-1)]-[f(x-1, y+1)
+ 2*f(x,y+1)+f(x+1,y+1)]
其中f(x,y), 表示图像(x,y)点的灰度值;
如果梯度G大于某一阀值 则认为该点(x,y)为边缘点。
与Prewitt算子相比,Sobel算子对于象素位置的影响作了加权,因此效果更好。
然后可用以下公式计算梯度方向,从而可以推断边缘所在的方向:
上面的算子是利用一阶导数的信息,属于梯度算子范畴。
下面是基于二阶导数的边缘检测算子。
(4)Laplacian算子
Laplacian算子定义为 ,它的差分形式为
表示成模板的形式就是
![]()
同理,如果是计算八邻域的二阶导数,模板就是:
可以看出,Laplace算子对孤立象素的响应要比对边缘或线的响应要更强烈,因此只适用于无噪声
图象。首先对图像进行高斯卷积滤波进行降噪处理,再采用Laplace算子进行边缘检测,就可以提高算子对
噪声和离散点的鲁棒性。也就是,先用高斯卷积核做滤波降噪,然后再求二阶导检测边缘。用公式表示如下:
![]()
其中,上面这个式子成立的依据是:
![]()
我们把LoG叫做高斯型Laplacian算子(Laplace of Gaussian)。
所以可以先对高斯函数进行偏导操作,然后进行卷积求解。
高斯卷积函数定义为:
![]()
![]()
![]()
因此,我们可以LOG核函数定义为:
![]()
滤波+高斯卷积两步结合,就是直接对有原图像做LoG卷积。高斯卷积的效果是使得图像变得平滑去噪
同时,可以利用零交叉性质来检测边缘。如下图所示:
所以,使用高斯型拉普拉斯算子的步骤为: 1)对原图像进行Log卷积 2)检测图像中的过零点( Zero Crossings,也即从负到正或从正到负,可以采用检查四邻域的方式)
4)抑制非极大值
仅仅得到全局的梯度并不足以确定边缘,因此为确定边缘,必须保留局部梯度最大的点,而抑制非极大
值。解决方法:利用梯度的方向。
四个扇区的标号为0到3,对应3*3邻域的四种可能组合。在每一点上,邻域的中心像素M与沿着梯度线的
两个像素相比。如果M的梯度值不比沿梯度线的两个相邻像素梯度值大,则令M=0。否则不变。这样就保留了
梯度的极大值,抑制了非极大值。
(5)用双阈值算法检测和连接边缘
对非极大值抑制图像作用两个阈值th1和th2,两者关系th1=0.4th2 (这里的0.4是统计图像的直方图,
对阈值进行判定得出的)。首先把梯度幅值的直方图(求出来,选取占直方图总数%多少(自己定,代码中
定义70%)所对应的梯度幅值为高阈值,高阈值的0.4为低阈值,这只是一种简单策略。也可以采用其他的。
我们把梯度值小于th1的像素的灰度值设为0,得到图像1。然后把梯度值小于th2的像素的灰度值设为0,
得到图像2。由于图像2的阈值较高,去除大部分噪音,但同时也损失了有用的边缘信息。而图像1的阈值较低
,保留了较多的信息,我们可以以图像2为基础,以图像1为补充来连结图像的边缘。
链接边缘的具体步骤如下:
对图像2进行扫描,当遇到一个非零灰度的像素p(x,y)时,跟踪以p(x,y)为开始点的轮廓线,直到轮廓线
的终点q(x,y)。
考察图像1中与图像2中q(x,y)点位置对应的点s(x,y)的8邻近区域。如果在s(x,y)点的8邻近区域中有非
零像素s(x,y)存在,则将其包括到图像2中,作为r(x,y)点。从r(x,y)开始,重复第一步,直到我们在图像1
和图像2中都无法继续为止。
当完成对包含p(x,y)的轮廓线的连结之后,将这条轮廓线标记为已经访问。回到第一步,寻找下一条轮
廓线。重复第一步、第二步、第三步,直到图像2中找不到新轮廓线为止。