神经网络的图像识别技术,神经网络的层数怎么看

神经网络是不是层数越多越好？

1、神经网络算法隐含层的选取1.1构造法首先运用三种确定隐含层层数的方法得到三个隐含层层数，找到最小值和最大值，然后从最小值开始逐个验证模型预测误差，直到达到最大值。

最后选取模型误差最小的那个隐含层层数。该方法适用于双隐含层网络。1.2删除法单隐含层网络非线性映射能力较弱，相同问题，为达到预定映射关系，隐层节点要多一些，以增加网络的可调参数，故适合运用删除法。

1.3黄金分割法算法的主要思想:首先在[a,b]内寻找理想的隐含层节点数，这样就充分保证了网络的逼近能力和泛化能力。

为满足高精度逼近的要求，再按照黄金分割原理拓展搜索区间，即得到区间[b,c](其中b=0.619*(c-a)+a)，在区间[b,c]中搜索最优，则得到逼近能力更强的隐含层节点数，在实际应用根据要求，从中选取其一即可。

BP算法中,权值和阈值是每训练一次，调整一次。逐步试验得到隐层节点数就是先设置一个初始值，然后在这个值的基础上逐渐增加，比较每次网络的预测性能，选择性能最好的对应的节点数作为隐含层神经元节点数。

什么是深度学习与机器视觉

深度学习框架，尤其是基于人工神经网络的框架可以追溯到1980年福岛邦彦提出的新认知机[2]，而人工神经网络的历史更为久远rfid。

1989年，燕乐存（YannLeCun）等人开始将1974年提出的标准反向传播算法[3]应用于深度神经网络，这一网络被用于手写邮政编码识别。

尽管算法可以成功执行，但计算代价非常巨大，神经网路的训练时间达到了3天，因而无法投入实际使用[4]。

许多因素导致了这一缓慢的训练过程，其中一种是由于尔根·施密德胡伯（JürgenSchmidhuber）的学生赛普·霍克赖特（SeppHochreiter）于1991年提出的梯度消失问题[5][6]。

与此同时，神经网络也受到了其他更加简单模型的挑战，支持向量机等模型在20世纪90年代到21世纪初成为更加流行的机器学习算法。“深度学习”这一概念从2007年前后开始受到关注。

当时，杰弗里·辛顿（GeoffreyHinton）和鲁斯兰·萨拉赫丁诺夫（RuslanSalakhutdinov）提出了一种在前馈神经网络中进行有效训练的算法。

这一算法将网络中的每一层视为无监督的受限玻尔兹曼机，再使用有监督的反向传播算法进行调优[7]。

在此之前的1992年，在更为普遍的情形下，施密德胡伯也曾在递归神经网络上提出一种类似的训练方法，并在实验中证明这一训练方法能够有效提高有监督学习的执行速度[8][9].自深度学习出现以来，它已成为很多领域，尤其是在计算机视觉和语音识别中，成为各种领先系统的一部分。

在通用的用于检验的数据集，例如语音识别中的TIMIT和图像识别中的ImageNet,Cifar10上的实验证明，深度学习能够提高识别的精度。硬件的进步也是深度学习重新获得关注的重要因素。

高性能图形处理器的出现极大地提高了数值和矩阵运算的速度，使得机器学习算法的运行时间得到了显著的缩短[10][11]。

基本概念[编辑]深度学习的基础是机器学习中的分散表示（distributedrepresentation）。分散表示假定观测值是由不同因子相互作用生成。

在此基础上，深度学习进一步假定这一相互作用的过程可分为多个层次，代表对观测值的多层抽象。不同的层数和层的规模可用于不同程度的抽象[1]。

深度学习运用了这分层次抽象的思想，更高层次的概念从低层次的概念学习得到。

这一分层结构常常使用贪婪算法逐层构建而成，并从中选取有助于机器学习的更有效的特征[1].不少深度学习算法都以无监督学习的形式出现，因而这些算法能被应用于其他算法无法企及的无标签数据，这一类数据比有标签数据更丰富，也更容易获得。

这一点也为深度学习赢得了重要的优势[1]。人工神经网络下的深度学习[编辑]一部分最成功的深度学习方法涉及到对人工神经网络的运用。

人工神经网络受到了1959年由诺贝尔奖得主大卫·休伯尔（DavidH.Hubel）和托斯坦·威泽尔（TorstenWiesel）提出的理论启发。

休伯尔和威泽尔发现，在大脑的初级视觉皮层中存在两种细胞：简单细胞和复杂细胞，这两种细胞承担不同层次的视觉感知功能。受此启发，许多神经网络模型也被设计为不同节点之间的分层模型[12]。

福岛邦彦提出的新认知机引入了使用无监督学习训练的卷积神经网络。燕乐存将有监督的反向传播算法应用于这一架构[13]。

事实上，从反向传播算法自20世纪70年代提出以来，不少研究者都曾试图将其应用于训练有监督的深度神经网络，但最初的尝试大都失败。

赛普·霍克赖特（SeppHochreiter）在其博士论文中将失败的原因归结为梯度消失，这一现象同时在深度前馈神经网络和递归神经网络中出现，后者的训练过程类似深度网络。

在分层训练的过程中，本应用于修正模型参数的误差随着层数的增加指数递减，这导致了模型训练的效率低下[14][15]。为了解决这一问题，研究者们提出了一些不同的方法。

于尔根·施密德胡伯（JürgenSchmidhuber）于1992年提出多层级网络，利用无监督学习训练深度神经网络的每一层，再使用反向传播算法进行调优。

在这一模型中，神经网络中的每一层都代表观测变量的一种压缩表示，这一表示也被传递到下一层网络[8]。

另一种方法是赛普·霍克赖特和于尔根·施密德胡伯提出的长短期记忆神经网络（longshorttermmemory，LSTM）[16]。

2009年，在ICDAR2009举办的连笔手写识别竞赛中，在没有任何先验知识的情况下，深度多维长短期记忆神经网络取得了其中三场比赛的胜利[17][18]。

斯文·贝克提出了在训练时只依赖梯度符号的神经抽象金字塔模型，用以解决图像重建和人脸定位的问题[19]。

其他方法同样采用了无监督预训练来构建神经网络，用以发现有效的特征，此后再采用有监督的反向传播以区分有标签数据。辛顿等人于2006年提出的深度模型提出了使用多层隐变量学习高层表示的方法。

这一方法使用斯摩棱斯基于1986年提出的受限玻尔兹曼机[20]对每一个包含高层特征的层进行建模。模型保证了数据的对数似然下界随着层数的提升而递增。

当足够多的层数被学习完毕，这一深层结构成为一个生成模型，可以通过自上而下的采样重构整个数据集[21]。辛顿声称这一模型在高维结构化数据上能够有效低提取特征[22]。

吴恩达和杰夫·迪恩（JeffDean）领导的谷歌大脑（英语：GoogleBrain）团队创建了一个仅通过YouTube视频学习高层概念（例如猫）的神经网络[23][24]。

其他方法依赖了现代电子计算机的强大计算能力，尤其是GPU。

2010年，在于尔根·施密德胡伯位于瑞士人工智能实验室IDSIA的研究组中，丹·奇雷尚（DanCiresan）和他的同事展示了利用GPU直接执行反向传播算法而忽视梯度消失问题的存在。

这一方法在燕乐存等人给出的手写识别MNIST数据集上战胜了已有的其他方法[10]。

截止2011年，前馈神经网络深度学习中最新的方法是交替使用卷积层（convolutionallayers）和最大值池化层（max-poolinglayers）并加入单纯的分类层作为顶端。

训练过程也无需引入无监督的预训练[25][26]。从2011年起，这一方法的GPU实现[25]多次赢得了各类模式识别竞赛的胜利，包括IJCNN2011交通标志识别竞赛[27]和其他比赛。

这些深度学习算法也是最先在某些识别任务上达到和人类表现具备同等竞争力的算法[28]。深度学习结构[编辑]深度神经网络是一种具备至少一个隐层的神经网络。

与浅层神经网络类似，深度神经网络也能够为复杂非线性系统提供建模，但多出的层次为模型提供了更高的抽象层次，因而提高了模型的能力。

深度神经网络通常都是前馈神经网络，但也有语言建模等方面的研究将其拓展到递归神经网络[29]。

卷积深度神经网络（CovolutionalNeuronNetworks,CNN）在计算机视觉领域得到了成功的应用[30]。

此后，卷积神经网络也作为听觉模型被使用在自动语音识别领域，较以往的方法获得了更优的结果[31]。

深度神经网络[编辑]深度神经网络（deepneuronnetworks,DNN）是一种判别模型，可以使用反向传播算法进行训练。

权重更新可以使用下式进行随机梯度下降求解：其中，为学习率，为代价函数。这一函数的选择与学习的类型（例如监督学习、无监督学习、增强学习）以及激活函数相关。

例如，为了在一个多分类问题上进行监督学习，通常的选择是使用Softmax函数作为激活函数，而使用交叉熵作为代价函数。Softmax函数定义为，其中代表类别的概率，而和分别代表对单元和的输入。

交叉熵定义为，其中代表输出单元的目标概率，代表应用了激活函数后对单元的概率输出[32]。深度神经网络的问题[编辑]与其他神经网络模型类似，如果仅仅是简单地训练，深度神经网络可能会存在很多问题。

常见的两类问题是过拟合和过长的运算时间。深度神经网络很容易产生过拟合现象，因为增加的抽象层使得模型能够对训练数据中较为罕见的依赖关系进行建模。

对此，权重递减（正规化）或者稀疏（-正规化）等方法可以利用在训练过程中以减小过拟合现象[33]。

另一种较晚用于深度神经网络训练的正规化方法是丢弃法（"dropout"regularization），即在训练中随机丢弃一部分隐层单元来避免对较为罕见的依赖进行建模[34]。

反向传播算法和梯度下降法由于其实现简单，与其他方法相比能够收敛到更好的局部最优值而成为神经网络训练的通行方法。

但是，这些方法的计算代价很高，尤其是在训练深度神经网络时，因为深度神经网络的规模（即层数和每层的节点数）、学习率、初始权重等众多参数都需要考虑。

扫描所有参数由于时间代价的原因并不可行，因而小批量训练（mini-batching），即将多个训练样本组合进行训练而不是每次只使用一个样本进行训练，被用于加速模型训练[35]。

而最显著地速度提升来自GPU，因为矩阵和向量计算非常适合使用GPU实现。但使用大规模集群进行深度神经网络训练仍然存在困难，因而深度神经网络在训练并行化方面仍有提升的空间。

深度信念网络[编辑]一个包含完全连接可见层和隐层的受限玻尔兹曼机（RBM）。注意到可见层单元和隐层单元内部彼此不相连。

深度信念网络（deepbeliefnetworks，DBN）是一种包含多层隐单元的概率生成模型，可被视为多层简单学习模型组合而成的复合模型[36]。

深度信念网络可以作为深度神经网络的预训练部分，并为网络提供初始权重，再使用反向传播或者其他判定算法作为调优的手段。

这在训练数据较为缺乏时很有价值，因为不恰当的初始化权重会显著影响最终模型的性能，而预训练获得的权重在权值空间中比随机权重更接近最优的权重。这不仅提升了模型的性能，也加快了调优阶段的收敛速度[37]。

深度信念网络中的每一层都是典型的受限玻尔兹曼机（restrictedBoltzmannmachine，RBM），可以使用高效的无监督逐层训练方法进行训练。

受限玻尔兹曼机是一种无向的基于能量的生成模型，包含一个输入层和一个隐层。图中对的边仅在输入层和隐层之间存在，而输入层节点内部和隐层节点内部则不存在边。

单层RBM的训练方法最初由杰弗里·辛顿在训练“专家乘积”中提出，被称为对比分歧（contrastdivergence,CD）。

对比分歧提供了一种对最大似然的近似，被理想地用于学习受限玻尔兹曼机的权重[35]。当单层RBM被训练完毕后，另一层RBM可被堆叠在已经训练完成的RBM上，形成一个多层模型。

每次堆叠时，原有的多层网络输入层被初始化为训练样本，权重为先前训练得到的权重，该网络的输出作为新增RBM的输入，新的RBM重复先前的单层训练过程，整个过程可以持续进行，直到达到某个期望中的终止条件[38]。

尽管对比分歧对最大似然的近似十分粗略（对比分歧并不在任何函数的梯度方向上），但经验结果证实该方法是训练深度结构的一种有效的方法[35]。

卷积神经网络[编辑]主条目：卷积神经网络卷积神经网络（convolutionalneuronnetworks，CNN）由一个或多个卷积层和顶端的全连通层（对应经典的神经网络）组成，同时也包括关联权重和池化层（poolinglayer）。

这一结构使得卷积神经网络能够利用输入数据的二维结构。与其他深度学习结构相比，卷积神经网络在图像和语音识别方面能够给出更优的结果。这一模型也可以使用反向传播算法进行训练。

相比较其他深度、前馈神经网络，卷积神经网络需要估计的参数更少，使之成为一种颇具吸引力的深度学习结构[39]。

卷积深度信念网络[编辑]卷积深度信念网络（convolutionaldeepbeliefnetworks，CDBN）是深度学习领域较新的分支。

在结构上，卷积深度信念网络与卷积神经网络在结构上相似。因此，与卷积神经网络类似，卷积深度信念网络也具备利用图像二维结构的能力，与此同时，卷积深度信念网络也拥有深度信念网络的预训练优势。

卷积深度信念网络提供了一种能被用于信号和图像处理任务的通用结构，也能够使用类似深度信念网络的训练方法进行训练[40]。

结果[编辑]语音识别[编辑]下表中的结果展示了深度学习在通行的TIMIT数据集上的结果。TIMIT包含630人的语音数据，这些人持八种常见的美式英语口音，每人阅读10句话。

这一数据在深度学习发展之初常被用于验证深度学习结构[41]。TIMIT数据集较小，使得研究者可以在其上实验不同的模型配置。

方法声音误差率(PER,%)随机初始化RNN26.1贝叶斯三音子GMM-HMM25.6单音子重复初始化DNN23.4单音子DBN-DNN22.4带BMMI训练的三音子GMM-HMM21.7共享池上的单音子DBN-DNN20.7卷积DNN20.0图像分类[编辑]图像分类领域中一个公认的评判数据集是MNIST数据集。

MNIST由手写阿拉伯数字组成，包含60,000个训练样本和10,000个测试样本。与TIMIT类似，它的数据规模较小，因而能够很容易地在不同的模型配置下测试。

YannLeCun的网站给出了多种方法得到的实验结果[42]。截至2012年，最好的判别结果由Ciresan等人在当年给出，这一结果的错误率达到了0.23%[43]。

深度学习与神经科学[编辑]计算机领域中的深度学习与20世纪90年代由认知神经科学研究者提出的大脑发育理论（尤其是皮层发育理论）密切相关[44]。

对这一理论最容易理解的是杰弗里·艾尔曼（JeffreyElman）于1996年出版的专著《对天赋的再思考》（RethinkingInnateness）[45]（参见斯拉格和约翰逊[46]以及奎兹和赛杰诺维斯基[47]的表述）。

由于这些理论给出了实际的神经计算模型，因而它们是纯计算驱动的深度学习模型的技术先驱。这些理论指出，大脑中的神经元组成了不同的层次，这些层次相互连接，形成一个过滤体系。

在这些层次中，每层神经元在其所处的环境中获取一部分信息，经过处理后向更深的层级传递。这与后来的单纯与计算相关的深度神经网络模型相似。这一过程的结果是一个与环境相协调的自组织的堆栈式的转换器。

正如1995年在《纽约时报》上刊登的那样，“……婴儿的大脑似乎受到所谓‘营养因素’的影响而进行着自我组织……大脑的不同区域依次相连，不同层次的脑组织依照一定的先后顺序发育成熟，直至整个大脑发育成熟。

”[48]深度结构在人类认知演化和发展中的重要性也在认知神经学家的关注之中。发育时间的改变被认为是人类和其他灵长类动物之间智力发展差异的一个方面[49]。

在灵长类中，人类的大脑在出生后的很长时间都具备可塑性，但其他灵长类动物的大脑则在出生时就几乎完全定型。

因而，人类在大脑发育最具可塑性的阶段能够接触到更加复杂的外部场景，这可能帮助人类的大脑进行调节以适应快速变化的环境，而不是像其他动物的大脑那样更多地受到遗传结构的限制。

这样的发育时间差异也在大脑皮层的发育时间和大脑早期自组织中从刺激环境中获取信息的改变得到体现。当然，伴随着这一可塑性的是更长的儿童期，在此期间人需要依靠抚养者和社会群体的支持和训练。

因而这一理论也揭示了人类演化中文化和意识共同进化的现象[50]。公众视野中的深度学习[编辑]深度学习常常被看作是通向真正人工智能的重要一步[51]，因而许多机构对深度学习的实际应用抱有浓厚的兴趣。

2013年12月，Facebook宣布雇用燕乐存为其新建的人工智能实验室的主管，这一实验室将在加州、伦敦和纽约设立分支机构，帮助Facebook研究利用深度学习算法进行类似自动标记照片中用户姓名这样的任务[52]。

2013年3月，杰弗里·辛顿和他的两位研究生亚历克斯·克里泽夫斯基和伊利娅·苏特斯科娃被谷歌公司雇用，以提升现有的机器学习产品并协助处理谷歌日益增长的数据。

谷歌同时并购了辛顿创办的公司DNNresearch[53]。批评[编辑]对深度学习的主要批评是许多方法缺乏理论支撑。大多数深度结构仅仅是梯度下降的某些变式。

尽管梯度下降已经被充分地研究，但理论涉及的其他算法，例如对比分歧算法，并没有获得充分的研究，其收敛性等问题仍不明确。深度学习方法常常被视为黑盒，大多数的结论确认都由经验而非理论来确定。

也有学者认为，深度学习应当被视为通向真正人工智能的一条途径，而不是一种包罗万象的解决方案。尽管深度学习的能力很强，但和真正的人工智能相比，仍然缺乏诸多重要的能力。

理论心理学家加里·马库斯（GaryMarcus）指出：就现实而言，深度学习只是建造智能机器这一更大挑战中的一部分。

这些技术缺乏表达因果关系的手段……缺乏进行逻辑推理的方法，而且远没有具备集成抽象知识，例如物品属性、代表和典型用途的信息。

最为强大的人工智能系统，例如IBM的人工智能系统沃森，仅仅把深度学习作为一个包含从贝叶斯推理和演绎推理等技术的复杂技术集合中的组成部分[54]。

yolov4卷积神经网络有多少卷积层

神经网络包括卷积层，还包括哪些层

卷积神经网络（ConvolutionalNeuralNetwork,CNN）是一种前馈神经网络，它的人工神经元可以响应一部分覆盖范围内的周围单元，对于大型图像处理有出色表现。

[1]它包括卷积层(alternatingconvolutionallayer)和池层(poolinglayer)。卷积神经网络是近年发展起来，并引起广泛重视的一种高效识别方法。

20世纪60年代，Hubel和Wiesel在研究猫脑皮层中用于局部敏感和方向选择的神经元时发现其独特的网络结构可以有效地降低反馈神经网络的复杂性，继而提出了卷积神经网络（ConvolutionalNeuralNetworks-简称CNN）。

现在，CNN已经成为众多科学领域的研究热点之一，特别是在模式分类领域，由于该网络避免了对图像的复杂前期预处理，可以直接输入原始图像，因而得到了更为广泛的应用。

K.Fukushima在1980年提出的新识别机是卷积神经网络的第一个实现网络。随后，更多的科研工作者对该网络进行了改进。

其中，具有代表性的研究成果是Alexander和Taylor提出的“改进认知机”，该方法综合了各种改进方法的优点并避免了耗时的误差反向传播。

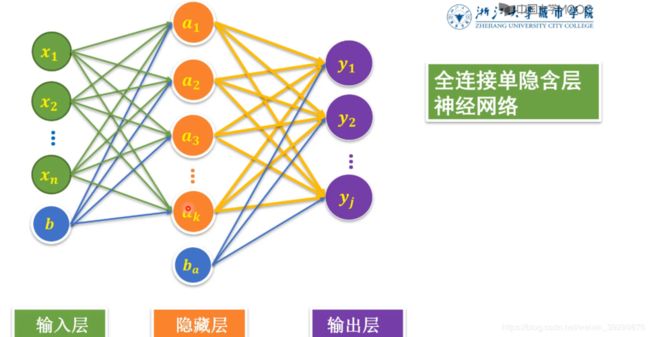
请问如何确定神经网络控制中网络层数和每层神经元个数

目前最常用的神经网络是多少层的

一般认为，增加隐层数可以降低网络误差（也有文献认为不一定能有效降低），提高精度，但也使网络复杂化，从而增加了网络的训练时间和出现“过拟合”的倾向。

一般来讲应设计神经网络应优先考虑3层网络（即有1个隐层）。一般地，靠增加隐层节点数来获得较低的误差，其训练效果要比增加隐层数更容易实现。

对于没有隐层的神经网络模型，实际上就是一个线性或非线性（取决于输出层采用线性或非线性转换函数型式）回归模型。

因此，一般认为，应将不含隐层的网络模型归入回归分析中，技术已很成熟，没有必要在神经网络理论中再讨论之。

如何通过人工神经网络实现图像识别

。

人工神经网络（ArtificialNeuralNetworks）（简称ANN）系统从20世纪40年代末诞生至今仅短短半个多世纪，但由于他具有信息的分布存储、并行处理以及自学习能力等优点，已经在信息处理、模式识别、智能控制及系统建模等领域得到越来越广泛的应用。

尤其是基于误差反向传播（ErrorBackPropagation）算法的多层前馈网络（Multiple-LayerFeedforwardNetwork）(简称BP网络)，可以以任意精度逼近任意的连续函数，所以广泛应用于非线性建模、函数逼近、模式分类等方面。

目标识别是模式识别领域的一项传统的课题，这是因为目标识别不是一个孤立的问题，而是模式识别领域中大多数课题都会遇到的基本问题，并且在不同的课题中，由于具体的条件不同，解决的方法也不尽相同，因而目标识别的研究仍具有理论和实践意义。

这里讨论的是将要识别的目标物体用成像头(红外或可见光等)摄入后形成的图像信号序列送入计算机，用神经网络识别图像的问题。

一、BP神经网络BP网络是采用Widrow-Hoff学习算法和非线性可微转移函数的多层网络。一个典型的BP网络采用的是梯度下降算法，也就是Widrow-Hoff算法所规定的。

backpropagation就是指的为非线性多层网络计算梯度的方法。一个典型的BP网络结构如图所示。我们将它用向量图表示如下图所示。

其中：对于第k个模式对，输出层单元的j的加权输入为该单元的实际输出为而隐含层单元i的加权输入为该单元的实际输出为函数f为可微分递减函数其算法描述如下：（1）初始化网络及学习参数，如设置网络初始权矩阵、学习因子等。

（2）提供训练模式，训练网络，直到满足学习要求。（3）前向传播过程：对给定训练模式输入，计算网络的输出模式，并与期望模式比较，若有误差，则执行（4）；否则，返回（2）。

（4）后向传播过程：a.计算同一层单元的误差；b.修正权值和阈值；c.返回（2）二、BP网络隐层个数的选择对于含有一个隐层的三层BP网络可以实现输入到输出的任何非线性映射。

增加网络隐层数可以降低误差，提高精度，但同时也使网络复杂化，增加网络的训练时间。误差精度的提高也可以通过增加隐层结点数来实现。一般情况下，应优先考虑增加隐含层的结点数。

三、隐含层神经元个数的选择当用神经网络实现网络映射时，隐含层神经元个数直接影响着神经网络的学习能力和归纳能力。

隐含层神经元数目较少时，网络每次学习的时间较短，但有可能因为学习不足导致网络无法记住全部学习内容；隐含层神经元数目较大时，学习能力增强，网络每次学习的时间较长，网络的存储容量随之变大，导致网络对未知输入的归纳能力下降，因为对隐含层神经元个数的选择尚无理论上的指导，一般凭经验确定。

四、神经网络图像识别系统人工神经网络方法实现模式识别，可处理一些环境信息十分复杂，背景知识不清楚，推理规则不明确的问题，允许样品有较大的缺损、畸变，神经网络方法的缺点是其模型在不断丰富完善中，目前能识别的模式类还不够多，神经网络方法允许样品有较大的缺损和畸变，其运行速度快，自适应性能好，具有较高的分辨率。

神经网络的图像识别系统是神经网络模式识别系统的一种，原理是一致的。一般神经网络图像识别系统由预处理，特征提取和神经网络分类器组成。预处理就是将原始数据中的无用信息删除，平滑，二值化和进行幅度归一化等。

神经网络图像识别系统中的特征提取部分不一定存在，这样就分为两大类：①有特征提取部分的：这一类系统实际上是传统方法与神经网络方法技术的结合，这种方法可以充分利用人的经验来获取模式特征以及神经网络分类能力来识别目标图像。

特征提取必须能反应整个图像的特征。但它的抗干扰能力不如第2类。

②无特征提取部分的：省去特征抽取，整副图像直接作为神经网络的输入，这种方式下，系统的神经网络结构的复杂度大大增加了，输入模式维数的增加导致了网络规模的庞大。

此外，神经网络结构需要完全自己消除模式变形的影响。但是网络的抗干扰性能好，识别率高。当BP网用于分类时，首先要选择各类的样本进行训练，每类样本的个数要近似相等。

其原因在于一方面防止训练后网络对样本多的类别响应过于敏感，而对样本数少的类别不敏感。另一方面可以大幅度提高训练速度，避免网络陷入局部最小点。

由于BP网络不具有不变识别的能力，所以要使网络对模式的平移、旋转、伸缩具有不变性，要尽可能选择各种可能情况的样本。

例如要选择不同姿态、不同方位、不同角度、不同背景等有代表性的样本，这样可以保证网络有较高的识别率。

构造神经网络分类器首先要选择适当的网络结构：神经网络分类器的输入就是图像的特征向量；神经网络分类器的输出节点应该是类别数。隐层数要选好，每层神经元数要合适，目前有很多采用一层隐层的网络结构。

然后要选择适当的学习算法，这样才会有很好的识别效果。

在学习阶段应该用大量的样本进行训练学习，通过样本的大量学习对神经网络的各层网络的连接权值进行修正，使其对样本有正确的识别结果，这就像人记数字一样，网络中的神经元就像是人脑细胞，权值的改变就像是人脑细胞的相互作用的改变，神经网络在样本学习中就像人记数字一样，学习样本时的网络权值调整就相当于人记住各个数字的形象，网络权值就是网络记住的内容，网络学习阶段就像人由不认识数字到认识数字反复学习过程是一样的。

神经网络是按整个特征向量的整体来记忆图像的，只要大多数特征符合曾学习过的样本就可识别为同一类别，所以当样本存在较大噪声时神经网络分类器仍可正确识别。

在图像识别阶段，只要将图像的点阵向量作为神经网络分类器的输入，经过网络的计算，分类器的输出就是识别结果。五、仿真实验1、实验对象本实验用MATLAB完成了对神经网络的训练和图像识别模拟。

从实验数据库中选择0～9这十个数字的BMP格式的目标图像。图像大小为16×8像素，每个目标图像分别加10％、20％、30％、40％、50％大小的随机噪声，共产生60个图像样本。

将样本分为两个部分，一部分用于训练，另一部分用于测试。实验中用于训练的样本为40个，用于测试的样本为20个。随机噪声调用函数randn(m,n)产生。

2、网络结构本试验采用三层的BP网络，输入层神经元个数等于样本图像的象素个数16×8个。隐含层选24个神经元，这是在试验中试出的较理想的隐层结点数。

输出层神经元个数就是要识别的模式数目，此例中有10个模式，所以输出层神经元选择10个，10个神经元与10个模式一一对应。

3、基于MATLAB语言的网络训练与仿真建立并初始化网络% ================S1 = 24;% 隐层神经元数目S1 选为24[R,Q] = size(numdata);[S2,Q] = size(targets);F = numdata;P=double(F);net = newff(minmax(P),[S1 S2],{'logsig''logsig'},'traingda','learngdm')这里numdata为训练样本矩阵，大小为128×40，targets为对应的目标输出矩阵，大小为10×40。

newff(PR,[S1S2…SN],{TF1TF2…TFN}，BTF,BLF,PF)为MATLAB函数库中建立一个N层前向BP网络的函数，函数的自变量PR表示网络输入矢量取值范围的矩阵[Pminmax];S1~SN为各层神经元的个数；TF1~TFN用于指定各层神经元的传递函数；BTF用于指定网络的训练函数；BLF用于指定权值和阀值的学习函数；PF用于指定网络的性能函数，缺省值为‘mse’。

设置训练参数net.performFcn = 'sse'; %平方和误差性能函数 = 0.1; %平方和误差目标 = 20; %进程显示频率net.trainParam.epochs = 5000;%最大训练步数 = 0.95; %动量常数网络训练net=init(net);%初始化网络[net,tr] = train(net,P,T);％网络训练对训练好的网络进行仿真D=sim(net,P);A = sim(net,B);B为测试样本向量集,128×20的点阵。

D为网络对训练样本的识别结果，A为测试样本的网络识别结果。实验结果表明：网络对训练样本和对测试样本的识别率均为100％。如图为64579五个数字添加50%随机噪声后网络的识别结果。

六、总结从上述的试验中已经可以看出，采用神经网络识别是切实可行的，给出的例子只是简单的数字识别实验，要想在网络模式下识别复杂的目标图像则需要降低网络规模，增加识别能力，原理是一样的。

神经网络层数包括输入和输出层吗

bp神经网络如何区分单层和多层隐藏

。

这个全靠你自己设的,你喜欢设几层就设几层,不过一般来说,BP都是一个输入层,一个隐层,一个输出层这样.因为听说一个隐层就能够逼近任意的函数了.你如果是用matlab工具箱的话,你可以调用net.numLayers查看网络的层数,若果是2,则说明是一个隐层(你可以认为matlab把输出也当一个隐层),是3,则有2个隐层,这样类推.学习神经网络可以上。