CS231n-assignment3-Self-Supervised Learning
什么是自我监督学习?
现代机器学习需要大量的标记数据。但通常情况下,获取大量人类标记数据是具有挑战性和/昂贵的。有没有一种方法,我们可以让机器自动学习一个模型,可以生成良好的视觉表示,而无需标记数据集?是的,自我监督学习!
自我监督学习(SSL)允许模型使用给定数据集中的数据自动学习“好的”表现空间,而不需要标签。具体来说,如果我们的数据集是一堆图像,那么自我监督学习允许模型学习并生成“好的”图像表现向量。
SSL方法之所以如此流行,是因为学习后的模型在其他数据集上仍然表现良好,例如没有在其上训练过的新数据集!
什么是“好的”表现?
一个“好的”表现向量需要捕获图像的重要特征,因为它与数据集的其余部分相关。这意味着表现语义相似实体的数据集中的图像应该有相似的表现向量,数据集中不同的图像应该有不同的表现向量。例如,两个苹果的图像应该有相似的表现向量,而苹果的图像和香蕉的图像应该有不同的表现向量。
对比学习:SimCLR
最近,SimCLR引入了一种新的体系结构,它使用对比学习来学习好的视觉表现。对比学习的目的是对相似图像学习相似表示,对不同图像学习不同表示。正如我们将在这个笔记本中看到的,这个简单的想法允许我们训练一个惊人的好模型而不使用任何标签。
具体来说,对于数据集中的每个图像,SimCLR生成该图像的两个不同的增强视图,称为正对。然后,鼓励该模型为这对图像生成相似的表现向量。
ln[1]:
# Run this cell to view the SimCLR architecture.
from IPython.display import Image
Image('images/simclr_fig2.png', width=500)
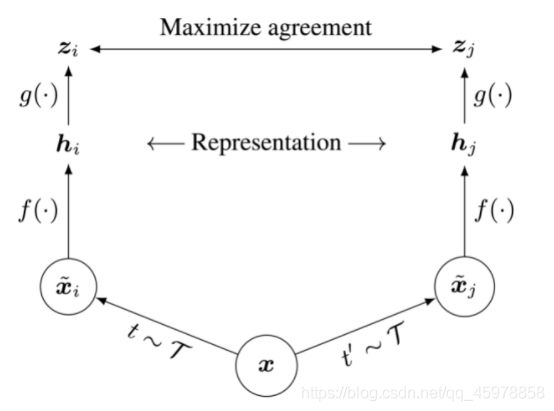
给定图像x, SimCLR使用两种不同的数据增强方案t和t’生成正数对图像̂和̂。是一个基本的编码器网络,它从扩展的数据样本中提取表示向量,分别生成ℎ和ℎ。最后,一个小的神经网络投影头将表示向量映射到应用对比损耗的空间。对比损失的目标是使最终向量=(ℎ)和=(ℎ)之间的一致性最大化。稍后我们将更详细地讨论对比损耗,您将实现它。
训练完成后,我们扔掉投影头,只使用和表示法ℎ来完成下游的任务,如分类等。您将有机会为分类任务优化训练过的SimCLR模型之上的一个层,并将其性能与基线模型进行比较(不需要自我监督学习)。
Pretrained Weights
为了方便您,我们为SimCLR模型提供了预先训练的重量(在CIFAR-10上训练了约18个小时)。运行以下单元以下载稍后使用的预训练模型权重。(这需要大约1分钟)
ln[2]:
# Setup cell.
#%pip install thop
import torch
import os
import importlib
import pandas as pd
import numpy as np
import torch.optim as optim
import torch.nn as nn
import random
from thop import profile, clever_format
from torch.utils.data import DataLoader
from torchvision.datasets import CIFAR10
import matplotlib.pyplot as plt
%matplotlib inline
%load_ext autoreload
%autoreload 2
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
Data Augmentation(数据增强):
我们的第一步是执行数据增强。在cs231n/simclr/data_utils.py中实现compute_train_transform()函数,以应用以下随机转换:
1.随机调整大小和裁剪到32x32。
2.以0.5的概率水平翻转图像
3.使用0.8的概率,应用颜色抖动(参见compute_train_transform()的定义)
4.概率为0.2,将图像转换为灰度
现在在cs231n/simclr/data_utils.py中完成compute_train_transform()和CIFAR10Pair.getitem(),以应用数据扩展转换并生成̂和̂。
def compute_train_transform(seed=123456):
"""
This function returns a composition of data augmentations to a single training image.
Complete the following lines. Hint: look at available functions in torchvision.transforms
"""
random.seed(seed)
torch.random.manual_seed(seed)
# Transformation that applies color jitter with brightness=0.4, contrast=0.4, saturation=0.4, and hue=0.1
color_jitter = transforms.ColorJitter(0.4, 0.4, 0.4, 0.1)
train_transform = transforms.Compose([
##############################################################################
# TODO: Start of your code. #
# #
# Hint: Check out transformation functions defined in torchvision.transforms #
# The first operation is filled out for you as an example.
##############################################################################
# Step 1: Randomly resize and crop to 32x32.
transforms.RandomResizedCrop(32),
# Step 2: Horizontally flip the image with probability 0.5
transforms.RandomHorizontalFlip(p=0.5),
# Step 3: With a probability of 0.8, apply color jitter (you can use "color_jitter" defined above.
transforms.RandomApply(torch.nn.ModuleList([color_jitter]), p=0.8),
# Step 4: With a probability of 0.2, convert the image to grayscale
transforms.RandomGrayscale(p=0.2),
##############################################################################
# END OF YOUR CODE #
##############################################################################
transforms.ToTensor(),
transforms.Normalize([0.4914, 0.4822, 0.4465], [0.2023, 0.1994, 0.2010])])
return train_transform
def compute_test_transform():
test_transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize([0.4914, 0.4822, 0.4465], [0.2023, 0.1994, 0.2010])])
return test_transform
class CIFAR10Pair(CIFAR10):
"""CIFAR10 Dataset.
"""
def __getitem__(self, index):
img, target = self.data[index], self.targets[index]
img = Image.fromarray(img)
x_i = None
x_j = None
if self.transform is not None:
##############################################################################
# TODO: Start of your code. #
# #
# Apply self.transform to the image to produce x_i and x_j in the paper #
##############################################################################
x_i = self.transform(img)
x_j = self.transform(img)
##############################################################################
# END OF YOUR CODE #
##############################################################################
if self.target_transform is not None:
target = self.target_transform(target)
return x_i, x_j, target
测试以确保你的数据增强代码是正确的:
ln[5]:
from cs231n.simclr.data_utils import *
from cs231n.simclr.contrastive_loss import *
answers = torch.load('simclr_sanity_check.key')
ln[6]:
from PIL import Image
import torchvision
from torchvision.datasets import CIFAR10
def test_data_augmentation(correct_output=None):
train_transform = compute_train_transform(seed=2147483647)
trainset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=train_transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=2, shuffle=False, num_workers=2)
dataiter = iter(trainloader)
images, labels = dataiter.next()
img = torchvision.utils.make_grid(images)
img = img / 2 + 0.5 # unnormalize
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
plt.show()
output = images
print("Maximum error in data augmentation: %g"%rel_error( output.numpy(), correct_output.numpy()))
# Should be less than 1e-07.
test_data_augmentation(answers['data_augmentation'])

基础编码器和投影头
基础编码器提取增强样本的表示向量。SimCLR论文发现,使用更深更广的模型可以提高性能,因此选择ResNet作为基础编码器。基本编码器的输出是表示向量ℎ=(̂)和ℎ=(̂)。
投影头是一个小的神经网络,它将表示向量ℎ和ℎ映射到应用对比损耗的空间。采用非线性投影头可以提高前一层的表示质量。具体来说,使用了一个带有一个隐藏层的MLP作为投影头。然后根据输出=(ℎ)和=(ℎ)计算对比损失。
我们在cs231n/simclr/model.py中提供了这两个部分的实现。请浏览文件,并确保您理解了实现。
SimCLR:对比损失
一小批训练图像共生成2数据增强示例。对于每一个增强例子的正数对(,),对比损失函数的目标是使向量和的一致性最大化。具体来说,损失是标准化temperature-scaled交叉熵的损失,目的是最大化和相对于批内所有其他增强示例的一致性:
l ( i , j ) = − log exp ( sim ( z i , z j ) / τ ) ∑ k = 1 2 N 1 k ≠ i exp ( sim ( z i , z k ) / τ ) l \; (i, j) = -\log \frac{\exp (\;\text{sim}(z_i, z_j)\; / \;\tau) }{\sum_{k=1}^{2N} \mathbb{1}_{k \neq i} \exp (\;\text{sim} (z_i, z_k) \;/ \;\tau) } l(i,j)=−log∑k=12N1k=iexp(sim(zi,zk)/τ)exp(sim(zi,zj)/τ)
其中∈{0,1}是指示函数,如果≠,则输出1,否则输出0。是一个temperature参数,它决定了指数增长的速度。
s i m ( z i , z j ) = z i ⋅ z j ∣ ∣ z i ∣ ∣ ∣ ∣ z j ∣ ∣ sim(z_i, z_j) = \frac{z_i \cdot z_j}{|| z_i || || z_j ||} sim(zi,zj)=∣∣zi∣∣∣∣zj∣∣zi⋅zj(标准化)的点积向量和。与相似度越高,点积越大,分子也越大。分母通过对和批处理中所有其他增强示例进行求和来规范化值。标准化值的范围是(0,1),其中接近1的高分对应的是正数对(,)之间的高度相似性,以及与批处理中其他增强示例之间的低相似性。负对数然后将范围(0,1)映射到损失值(inf,0)。
计算批中的所有正对(,)的总损失。让=[1,2,…,2]包括批处理中的所有增强示例,其中1…是左分支的输出,+1…2是右分支的输出。因此,积极的对是(,+)∀∈(1,)。
则总损失为:
L = 1 2 N ∑ k = 1 N [ l ( k , k + N ) + l ( k + N , k ) ] L = \frac{1}{2N} \sum_{k=1}^N [ \; l(k, \;k+N) + l(k+N, \;k)\;] L=2N1∑k=1N[l(k,k+N)+l(k+N,k)]
完成sim, simclr_loss_naive in cs231n/simclr/contrastive_loss.py
def sim(z_i, z_j):
"""Normalized dot product between two vectors.
Inputs:
- z_i: 1xD tensor.
- z_j: 1xD tensor.
Returns:
- A scalar value that is the normalized dot product between z_i and z_j.
"""
norm_dot_product = None
##############################################################################
# TODO: Start of your code. #
# #
# HINT: torch.linalg.norm might be helpful. #
##############################################################################
z_i_normalized = z_i / torch.linalg.vector_norm(z_i)
z_j_normalized = z_j / torch.linalg.vector_norm(z_j)
norm_dot_product = torch.dot(z_i_normalized, z_j_normalized)
##############################################################################
# END OF YOUR CODE #
##############################################################################
return norm_dot_product
def simclr_loss_naive(out_left, out_right, tau):
"""Compute the contrastive loss L over a batch (naive loop version).
Input:
- out_left: NxD tensor; output of the projection head g(), left branch in SimCLR model.
- out_right: NxD tensor; output of the projection head g(), right branch in SimCLR model.
Each row is a z-vector for an augmented sample in the batch. The same row in out_left and out_right form a positive pair.
In other words, (out_left[k], out_right[k]) form a positive pair for all k=0...N-1.
- tau: scalar value, temperature parameter that determines how fast the exponential increases.
Returns:
- A scalar value; the total loss across all positive pairs in the batch. See notebook for definition.
"""
N = out_left.shape[0] # total number of training examples
# Concatenate out_left and out_right into a 2*N x D tensor.
out = torch.cat([out_left, out_right], dim=0) # [2*N, D]
total_loss = 0
for k in range(N): # loop through each positive pair (k, k+N)
z_k, z_k_N = out[k], out[k+N]
##############################################################################
# TODO: Start of your code. #
# #
# Hint: Compute l(k, k+N) and l(k+N, k). #
##############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
den_left, den_right = 0.0, 0.0
for j in range(2 * N):
if j != k:
den_left += torch.exp(sim(z_k, out[j]) / tau)
if j != N + k:
den_right += torch.exp(sim(z_k_N, out[j]) / tau)
loss_left = -torch.log(torch.exp(sim(z_k, z_k_N) / tau) / den_left)
loss_right = -torch.log(torch.exp(sim(z_k_N, z_k) / tau) / den_right)
total_loss += loss_left + loss_right
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
##############################################################################
# END OF YOUR CODE #
##############################################################################
# In the end, we need to divide the total loss by 2N, the number of samples in the batch.
total_loss = total_loss / (2*N)
return total_loss
def sim_positive_pairs(out_left, out_right):
"""Normalized dot product between positive pairs.
Inputs:
- out_left: NxD tensor; output of the projection head g(), left branch in SimCLR model.
- out_right: NxD tensor; output of the projection head g(), right branch in SimCLR model.
Each row is a z-vector for an augmented sample in the batch.
The same row in out_left and out_right form a positive pair.
Returns:
- A Nx1 tensor; each row k is the normalized dot product between out_left[k] and out_right[k].
"""
pos_pairs = None
##############################################################################
# TODO: Start of your code. #
# #
# HINT: torch.linalg.norm might be helpful. #
##############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
left_norm = out_left / torch.linalg.norm(out_left, dim=1, keepdims=True)
right_norm = out_right / torch.linalg.norm(out_right, dim=1, keepdims=True)
pos_pairs = torch.sum(left_norm * right_norm, dim=1, keepdims=True)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
##############################################################################
# END OF YOUR CODE #
##############################################################################
return pos_pairs
通过运行下面的完整性检查来测试代码。
ln[5]:
from cs231n.simclr.contrastive_loss import *
answers = torch.load('simclr_sanity_check.key')
ln[6]:
def test_sim(left_vec, right_vec, correct_output):
output = sim(left_vec, right_vec).cpu().numpy()
print("Maximum error in sim: %g"%rel_error(correct_output.numpy(), output))
# Should be less than 1e-07.
test_sim(answers['left'][0], answers['right'][0], answers['sim'][0])
test_sim(answers['left'][1], answers['right'][1], answers['sim'][1])
ln[7]:
def test_loss_naive(left, right, tau, correct_output):
naive_loss = simclr_loss_naive(left, right, tau).item()
print("Maximum error in simclr_loss_naive: %g"%rel_error(correct_output, naive_loss))
# Should be less than 1e-07.
test_loss_naive(answers['left'], answers['right'], 5.0, answers['loss']['5.0'])
test_loss_naive(answers['left'], answers['right'], 1.0, answers['loss']['1.0'])
![]()
现在通过实现实现矢量化的版本
sim_positive_pairs, compute_sim_matrix, simclr_loss_vectorized in cs231n/simclr/contrastive_loss.py
def sim_positive_pairs(out_left, out_right):
"""Normalized dot product between positive pairs.
Inputs:
- out_left: NxD tensor; output of the projection head g(), left branch in SimCLR model.
- out_right: NxD tensor; output of the projection head g(), right branch in SimCLR model.
Each row is a z-vector for an augmented sample in the batch.
The same row in out_left and out_right form a positive pair.
Returns:
- A Nx1 tensor; each row k is the normalized dot product between out_left[k] and out_right[k].
"""
pos_pairs = None
##############################################################################
# TODO: Start of your code. #
# #
# HINT: torch.linalg.norm might be helpful. #
##############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
left_norm = out_left / torch.linalg.norm(out_left, dim=1, keepdims=True)
right_norm = out_right / torch.linalg.norm(out_right, dim=1, keepdims=True)
pos_pairs = torch.sum(left_norm * right_norm, dim=1, keepdims=True)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
##############################################################################
# END OF YOUR CODE #
##############################################################################
return pos_pairs
def compute_sim_matrix(out):
"""Compute a 2N x 2N matrix of normalized dot products between all pairs of augmented examples in a batch.
Inputs:
- out: 2N x D tensor; each row is the z-vector (output of projection head) of a single augmented example.
There are a total of 2N augmented examples in the batch.
Returns:
- sim_matrix: 2N x 2N tensor; each element i, j in the matrix is the normalized dot product between out[i] and out[j].
"""
sim_matrix = None
##############################################################################
# TODO: Start of your code. #
##############################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
out_norm = out / torch.linalg.norm(out, dim=1, keepdims=True)
sim_matrix = torch.mm(out_norm, out_norm.T)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
##############################################################################
# END OF YOUR CODE #
##############################################################################
return sim_matrix
def simclr_loss_vectorized(out_left, out_right, tau, device='cuda'):
"""Compute the contrastive loss L over a batch (vectorized version). No loops are allowed.
Inputs and output are the same as in simclr_loss_naive.
"""
N = out_left.shape[0]
# Concatenate out_left and out_right into a 2*N x D tensor.
out = torch.cat([out_left, out_right], dim=0) # [2*N, D]
# Compute similarity matrix between all pairs of augmented examples in the batch.
sim_matrix = compute_sim_matrix(out) # [2*N, 2*N]
##############################################################################
# TODO: Start of your code. Follow the hints. #
##############################################################################
# Step 1: Use sim_matrix to compute the denominator value for all augmented samples.
# Hint: Compute e^{sim / tau} and store into exponential, which should have shape 2N x 2N.
exponential = torch.exp(sim_matrix.to(device) / tau) #分子
# This binary mask zeros out terms where k=i.
#torch.eye创建一个2维张量,对角线数字为1, 其他位置为0。也就是一个单位矩阵
mask = (torch.ones_like(exponential, device=device) - torch.eye(2 * N, device=device)).to(device).bool()
# We apply the binary mask.
exponential = exponential.masked_select(mask).view(2 * N, -1) # [2*N, 2*N-1]
# Hint: Compute the denominator values for all augmented samples. This should be a 2N x 1 vector.
denom = torch.sum(exponential, dim=1, keepdims=True)
# Step 2: Compute similarity between positive pairs.
# You can do this in two ways:
# Option 1: Extract the corresponding indices from sim_matrix.
# Option 2: Use sim_positive_pairs().
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
pos_pairs = sim_positive_pairs(out_left, out_right).to(device)
pos_pairs = torch.cat([pos_pairs, pos_pairs], dim=0)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# Step 3: Compute the numerator value for all augmented samples.
numerator = None
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
numerator = torch.exp(pos_pairs / tau)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# Step 4: Now that you have the numerator and denominator for all augmented samples, compute the total loss.
loss = torch.mean(-torch.log(numerator / denom))
##############################################################################
# END OF YOUR CODE #
##############################################################################
return loss
通过运行下面的完整性检查来测试代码。
ln[8]:
def test_sim_positive_pairs(left, right, correct_output):
sim_pair = sim_positive_pairs(left, right).cpu().numpy()
print("Maximum error in sim_positive_pairs: %g"%rel_error(correct_output.numpy(), sim_pair))
# Should be less than 1e-07.
test_sim_positive_pairs(answers['left'], answers['right'], answers['sim'])
def test_sim_matrix(left, right, correct_output):
out = torch.cat([left, right], dim=0)
sim_matrix = compute_sim_matrix(out).cpu()
assert torch.isclose(sim_matrix, correct_output).all(), "correct: {}. got: {}".format(correct_output, sim_matrix)
print("Test passed!")
test_sim_matrix(answers['left'], answers['right'], answers['sim_matrix'])
def test_loss_vectorized(left, right, tau, correct_output):
vec_loss = simclr_loss_vectorized(left, right, tau, device).item()
print("Maximum error in loss_vectorized: %g"%rel_error(correct_output, vec_loss))
# Should be less than 1e-07.
test_loss_vectorized(answers['left'], answers['right'], 5.0, answers['loss']['5.0'])
test_loss_vectorized(answers['left'], answers['right'], 1.0, answers['loss']['1.0'])
实现train function
在cs231n/simclr/utils.py中完成train()函数,得到模型的输出,并使用simclr_loss_vectoized计算损失。(请查看cs231n/simclr/ Model .py中的Model类,以理解模型管道和返回值)
def train(model, data_loader, train_optimizer, epoch, epochs, batch_size=32, temperature=0.5, device='cuda'):
"""Trains the model defined in ./model.py with one epoch.
Inputs:
- model: Model class object as defined in ./model.py.
- data_loader: torch.utils.data.DataLoader object; loads in training data. You can assume the loaded data has been augmented.
- train_optimizer: torch.optim.Optimizer object; applies an optimizer to training.
- epoch: integer; current epoch number.
- epochs: integer; total number of epochs.
- batch_size: Number of training samples per batch.
- temperature: float; temperature (tau) parameter used in simclr_loss_vectorized.
- device: the device name to define torch tensors.
Returns:
- The average loss.
"""
model.train()
total_loss, total_num, train_bar = 0.0, 0, tqdm(data_loader)
for data_pair in train_bar:
x_i, x_j, target = data_pair
x_i, x_j = x_i.to(device), x_j.to(device)
out_left, out_right, loss = None, None, None
##############################################################################
# TODO: Start of your code. #
# #
# Take a look at the model.py file to understand the model's input and output.
# Run x_i and x_j through the model to get out_left, out_right. #
# Then compute the loss using simclr_loss_vectorized. #
##############################################################################
_, out_left = model(x_i)
_, out_right = model(x_j)
loss = simclr_loss_vectorized(out_left, out_right, temperature)
##############################################################################
# END OF YOUR CODE #
##############################################################################
train_optimizer.zero_grad()
loss.backward()
train_optimizer.step()
total_num += batch_size
total_loss += loss.item() * batch_size
train_bar.set_description('Train Epoch: [{}/{}] Loss: {:.4f}'.format(epoch, epochs, total_loss / total_num))
return total_loss / total_num
ln[11]:
from cs231n.simclr.data_utils import *
from cs231n.simclr.model import *
from cs231n.simclr.utils import *
Train the SimCLR model
ln[12]:
# Do not modify this cell.
feature_dim = 128
temperature = 0.5
k = 200
batch_size = 64
epochs = 1
temperature = 0.5
percentage = 0.5
pretrained_path = './pretrained_model/pretrained_simclr_model.pth'
# Prepare the data.
train_transform = compute_train_transform()
train_data = CIFAR10Pair(root='data', train=True, transform=train_transform, download=True)
train_data = torch.utils.data.Subset(train_data, list(np.arange(int(len(train_data)*percentage))))
train_loader = DataLoader(train_data, batch_size=batch_size, shuffle=True, num_workers=16, pin_memory=True, drop_last=True)
test_transform = compute_test_transform()
memory_data = CIFAR10Pair(root='data', train=True, transform=test_transform, download=True)
memory_loader = DataLoader(memory_data, batch_size=batch_size, shuffle=False, num_workers=16, pin_memory=True)
test_data = CIFAR10Pair(root='data', train=False, transform=test_transform, download=True)
test_loader = DataLoader(test_data, batch_size=batch_size, shuffle=False, num_workers=16, pin_memory=True)
# Set up the model and optimizer config.
model = Model(feature_dim)
model.load_state_dict(torch.load(pretrained_path, map_location='cpu'), strict=False)
model = model.to(device)
flops, params = profile(model, inputs=(torch.randn(1, 3, 32, 32).to(device),))
flops, params = clever_format([flops, params])
print('# Model Params: {} FLOPs: {}'.format(params, flops))
optimizer = optim.Adam(model.parameters(), lr=1e-3, weight_decay=1e-6)
c = len(memory_data.classes)
# Training loop.
results = {'train_loss': [], 'test_acc@1': [], 'test_acc@5': []} #<< -- output
if not os.path.exists('results'):
os.mkdir('results')
best_acc = 0.0
for epoch in range(1, epochs + 1):
train_loss = train(model, train_loader, optimizer, epoch, epochs, batch_size=batch_size, temperature=temperature, device=device)
results['train_loss'].append(train_loss)
test_acc_1, test_acc_5 = test(model, memory_loader, test_loader, epoch, epochs, c, k=k, temperature=temperature, device=device)
results['test_acc@1'].append(test_acc_1)
results['test_acc@5'].append(test_acc_5)
# Save statistics.
if test_acc_1 > best_acc:
best_acc = test_acc_1
torch.save(model.state_dict(), './pretrained_model/trained_simclr_model.pth')
现在是测试表示向量的时候了!
我们将投影头从SimCLR模型中移除,并添加一个线性层,以便对简单的分类任务进行微调。对线性层之前的所有层进行冻结,只对最终线性层的权值进行训练。我们比较了SimCLR +微调模型与基线模型的性能,在基线模型中,没有进行自我监督学习,模型中的所有权重都经过训练。您将亲眼看到自我监督学习的力量,以及学习后的表示向量如何提高下游任务的性能。
Baseline: Without Self-Supervised Learning
首先,让我们看看Baseline模型。我们将从SimCLR模型中删除投影头部,并添加一个线性层,以便对简单的分类任务进行微调。事先不进行自我监督学习,对模型中的所有权重进行训练。运行以下单元格。
ln[13]:
class Classifier(nn.Module):
def __init__(self, num_class):
super(Classifier, self).__init__()
# Encoder.
self.f = Model().f
# Classifier.
self.fc = nn.Linear(2048, num_class, bias=True)
def forward(self, x):
x = self.f(x)
feature = torch.flatten(x, start_dim=1)
out = self.fc(feature)
return out
ln[14]:
# Do not modify this cell.
feature_dim = 128
temperature = 0.5
k = 200
batch_size = 128
epochs = 10
percentage = 0.1
train_transform = compute_train_transform()
train_data = CIFAR10(root='data', train=True, transform=train_transform, download=True)
trainset = torch.utils.data.Subset(train_data, list(np.arange(int(len(train_data)*percentage))))
train_loader = DataLoader(trainset, batch_size=batch_size, shuffle=True, num_workers=16, pin_memory=True)
test_transform = compute_test_transform()
test_data = CIFAR10(root='data', train=False, transform=test_transform, download=True)
test_loader = DataLoader(test_data, batch_size=batch_size, shuffle=False, num_workers=16, pin_memory=True)
model = Classifier(num_class=len(train_data.classes)).to(device)
for param in model.f.parameters():
param.requires_grad = False
flops, params = profile(model, inputs=(torch.randn(1, 3, 32, 32).to(device),))
flops, params = clever_format([flops, params])
print('# Model Params: {} FLOPs: {}'.format(params, flops))
optimizer = optim.Adam(model.fc.parameters(), lr=1e-3, weight_decay=1e-6)
no_pretrain_results = {'train_loss': [], 'train_acc@1': [], 'train_acc@5': [],
'test_loss': [], 'test_acc@1': [], 'test_acc@5': []}
best_acc = 0.0
for epoch in range(1, epochs + 1):
train_loss, train_acc_1, train_acc_5 = train_val(model, train_loader, optimizer, epoch, epochs, device='cuda')
no_pretrain_results['train_loss'].append(train_loss)
no_pretrain_results['train_acc@1'].append(train_acc_1)
no_pretrain_results['train_acc@5'].append(train_acc_5)
test_loss, test_acc_1, test_acc_5 = train_val(model, test_loader, None, epoch, epochs)
no_pretrain_results['test_loss'].append(test_loss)
no_pretrain_results['test_acc@1'].append(test_acc_1)
no_pretrain_results['test_acc@5'].append(test_acc_5)
if test_acc_1 > best_acc:
best_acc = test_acc_1
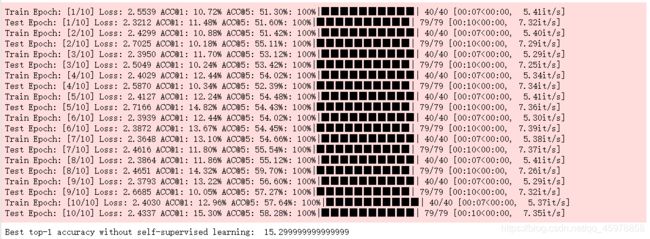
# Print the best test accuracy.
print('Best top-1 accuracy without self-supervised learning: ', best_acc)
With Self-Supervised Learning
ln[15]:
# Do not modify this cell.
feature_dim = 128
temperature = 0.5
k = 200
batch_size = 128
epochs = 10
percentage = 0.1
pretrained_path = './pretrained_model/trained_simclr_model.pth'
train_transform = compute_train_transform()
train_data = CIFAR10(root='data', train=True, transform=train_transform, download=True)
trainset = torch.utils.data.Subset(train_data, list(np.arange(int(len(train_data)*percentage))))
train_loader = DataLoader(trainset, batch_size=batch_size, shuffle=True, num_workers=16, pin_memory=True)
test_transform = compute_test_transform()
test_data = CIFAR10(root='data', train=False, transform=test_transform, download=True)
test_loader = DataLoader(test_data, batch_size=batch_size, shuffle=False, num_workers=16, pin_memory=True)
model = Classifier(num_class=len(train_data.classes))
model.load_state_dict(torch.load(pretrained_path, map_location='cpu'), strict=False)
model = model.to(device)
for param in model.f.parameters():
param.requires_grad = False
flops, params = profile(model, inputs=(torch.randn(1, 3, 32, 32).to(device),))
flops, params = clever_format([flops, params])
print('# Model Params: {} FLOPs: {}'.format(params, flops))
optimizer = optim.Adam(model.fc.parameters(), lr=1e-3, weight_decay=1e-6)
pretrain_results = {'train_loss': [], 'train_acc@1': [], 'train_acc@5': [],
'test_loss': [], 'test_acc@1': [], 'test_acc@5': []}
best_acc = 0.0
for epoch in range(1, epochs + 1):
train_loss, train_acc_1, train_acc_5 = train_val(model, train_loader, optimizer, epoch, epochs)
pretrain_results['train_loss'].append(train_loss)
pretrain_results['train_acc@1'].append(train_acc_1)
pretrain_results['train_acc@5'].append(train_acc_5)
test_loss, test_acc_1, test_acc_5 = train_val(model, test_loader, None, epoch, epochs)
pretrain_results['test_loss'].append(test_loss)
pretrain_results['test_acc@1'].append(test_acc_1)
pretrain_results['test_acc@5'].append(test_acc_5)
if test_acc_1 > best_acc:
best_acc = test_acc_1
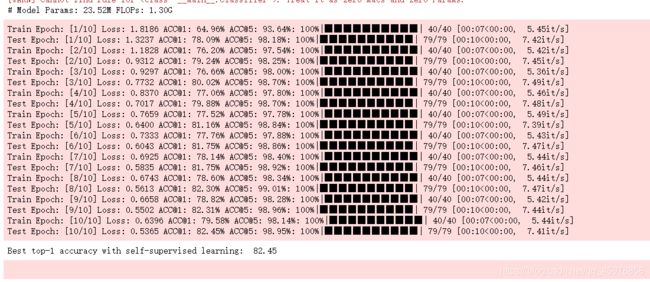
# Print the best test accuracy. You should see a best top-1 accuracy of >=70%.
print('Best top-1 accuracy with self-supervised learning: ', best_acc)
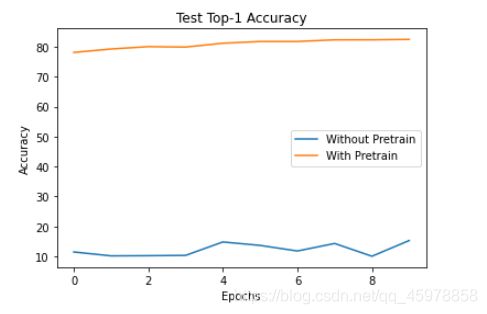
plt.plot(no_pretrain_results['test_acc@1'], label="Without Pretrain")
plt.plot(pretrain_results['test_acc@1'], label="With Pretrain")
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.title('Test Top-1 Accuracy')
plt.legend()
plt.show()