2020_WWW_The Structure of Social Influence in Recommender Networks

[论文阅读笔记]2020_WWW_The Structure of Social Influence in Recommender Networks

论文下载地址： https://doi.org/10.1145/3366423.3380020
发表期刊：WWW
Publish time: 2020
作者及单位:

• Pantelis P. Analytis∗ [email protected] University of Southern Denmark
• Daniel Barkoczi [email protected] University of Southern Denmark
• Philipp Lorenz-Spreen [email protected] Max Planck Institute for Human Development
• Stefan M. Herzog [email protected] Max Planck Institute for Human Development

数据集： 正文中的介绍

• Jester, a widely studied collaborative filtering dataset on humor collected by Goldberg and colleagues [19]; (Jester是Goldberg及其同事收集的一个广泛研究的关于幽默的协作过滤数据集[19]；)
  • [19] Ken Goldberg, Theresa Roeder, Dhruv Gupta, and Chris Perkins. 2001. Eigentaste: A constant time collaborative filtering algorithm. Information Retrieval 4, 2 (2001), 133–151.
• datasets on visual art, architecture, and landscapes collected by Vessel and colleagues [53]; (Vesser及其同事收集的视觉艺术、建筑和景观数据集[53]；)
  • [53] Edward A Vessel, Natalia Maurer, Alexander H Denker, and G Gabrielle Starr. 2018. Stronger shared taste for natural aesthetic domains than for artifacts of human culture. Cognition 179 (2018), 121–131.
• and data on the attractiveness of people’s faces collected by DeBruine and Jones [10]. (DeBruine和Jones收集的关于人脸吸引力的数据[10]。)
  • [10] Lisa DeBruine and Benedict Jones. 2017. Face Research Lab London Set. (5 2017).
    https://doi.org/10.6084/m9.figshare.5047666.v3
  • http://faceresearch.org/ (文中作者给出的)

代码：

• https://osf.io/duj8q/ (文中作者给出的)

其他：

其他人写的文章

简要概括创新点： 这是一篇偏理论分析的文章，用的weighted-KNN，然后就分析分析分析

• (1)We show three novel results that apply both to offline advice taking and online recommender settings. (我们展示了三个新的结果，它们同时适用于离线咨询和在线推荐设置)
  • First, influential individuals have mainstream tastes and high dispersion in their taste similarity with others. (首先，有影响力的人有主流口味，他们与他人的口味相似性高度分散。)
  • Second, the fewer people an individual or algorithm consults (i.e., the lower k is) or the larger the weight placed on the opinions of more similar others, the smaller the group of people with substantial influence. (第二，个人或算法咨询的人越少（即k越低），或者对更相似的人的意见的权重越大，具有重大影响的群体就越小。)
  • Third, the influence networks emerging from deploying the k-nn algorithm are hierarchically organized. (第三，部署k-nn算法产生的影响网络是分层组织的。)
• 细节
  • user之间的相似性用的皮尔逊相关系数
  • We used node strength, defined as the sum of the absolute weights2assigned to each of the $k$ nearest neighbors, as a measure of social influence that naturally fits the weighted $k-nn$ algorithm and weighted networks more generally [4]. 我们使用节点强度（定义为分配给每个$k$近邻的绝对权重之和）作为衡量社会影响力的指标，自然符合加权$k-nn$算法和更一般的加权网络[4]。这种通用方法也可用于在降维空间[34]上计算用户之间相似性的算法，或在使用关于个体的其他可观察信息来计算他们之间的相似性[21]时使用。)
  • In this case, node strength reduces to in-degree, the arguably most basic centrality measure. In our setting, in-degree represents the number of times a node (person) was sought for advice (or involved in the calculation of a recommendation). The analysis shows that in-degree varies greatly across people: For a wide range of values of $k$ there are only a few influential individuals (hubs; see Figure 3). (在这种情况下，节点强度降低到可以说是最基本的中心性度量。在我们的设置中，in-degree表示节点（人员）寻求建议（或参与建议计算）的次数。分析表明，不同的人在程度上差异很大：对于$k$值的广泛范围，只有少数有影响力的人（枢纽；见图3）。)
  • A second metric, the local clustering coefficient— which measures the extent to which an individual’s advisers also advise each other—is inversely related to the in-degree following the power law $C(d)=d^{-\beta }$: the less influence individuals exert over others, the tighter the clusters they tend to form (第二个指标是局部聚集系数，它衡量个人顾问之间相互建议的程度，与幂律$C(d)=d^{-\beta }$的程度成反比：个人对他人施加的影响越小，他们倾向于形成的集群就越紧密

ABSTRACT

• (1)People’s ability to influence others’ opinion on matters of taste varies greatly—both offline and in recommender systems. What are the mechanisms underlying these striking differences? Using the weighted k-nearest neighbors algorithm (k-nn) to represent an array of social learning strategies, we show—leveraging methods from network science—how the k-nn algorithm gives rise to networks of social influence in six real-world domains of taste. (无论是在网上还是在推荐系统中，人们在品味问题上影响他人意见的能力差异很大。这些显著差异背后的机制是什么？使用加权k-最近邻算法（k-nn）来表示一系列社会学习策略，我们展示了利用网络科学的方法，k-nn算法如何在六个现实世界的味觉领域产生社会影响网络。)
• (2)We show three novel results that apply both to offline advice taking and online recommender settings. (我们展示了三个新的结果，它们同时适用于离线咨询和在线推荐设置)
  • First, influential individuals have mainstream tastes and high dispersion in their taste similarity with others. (首先，有影响力的人有主流口味，他们与他人的口味相似性高度分散。)
  • Second, the fewer people an individual or algorithm consults (i.e., the lower k is) or the larger the weight placed on the opinions of more similar others, the smaller the group of people with substantial influence. (第二，个人或算法咨询的人越少（即k越低），或者对更相似的人的意见的权重越大，具有重大影响的群体就越小。)
  • Third, the influence networks emerging from deploying the k-nn algorithm are hierarchically organized. (第三，部署k-nn算法产生的影响网络是分层组织的。)
• (3)Our results shed new light on classic empirical findings in communication and network science and can help improve the understanding of social influence offline and online. (我们的研究结果为传播学和网络科学中的经典实证研究结果提供了新的线索，并有助于提高对线下和线上社会影响的理解。)

KEYWORDS

social influence, influencers, social networks, collaborative filtering

1 INTRODUCTION

• (1)We all have opinions on matters of taste. Whether it is a new song, the design of a building, or the performance of an actor, people are eager to express their opinions offline and online. However, the opinions of some are sought out and appreciated more than the opinions of others. Consider renowned film critics such as Roger Ebert or wine critics like Robert Parker: their opinions are recognized as an indicator of quality by most other critics and the general public alike—and can thus affect the price or financial success of a product [1, 5]. Relative to such highly influential individuals, most people exert little social influence over others. (对于品味问题，我们都有自己的看法。无论是新歌、建筑设计还是演员表演，人们都渴望在线下和网上表达自己的观点。然而，一些人的意见比其他人的意见更容易被寻求和欣赏。想想著名的影评家，比如Roger Ebert或像Robert Parker这样的葡萄酒评论家，他们的意见被大多数评论家和公众认为是质量的指示器，因此可以影响产品的价格或财务上的成功[ 1, 5 ]。与这些有影响力的人相比，大多数人对他人的社会影响力很小。)

• (2)Sociologists and communication scientists have been interested in the study of influential individuals since the mid-20th century, and understandably so. By accurately identifying individuals with influence, policy makers can sway public opinion on critical matters such as public health and the diffusion of socially beneficial innovations. Early studies [27, 33, 55] surveyed large numbers of people, typically residents of representative mid-sized cities in the United States, and asked them whom they would consult for advice in various domains (e.g., public health, fashion, politics). This early work revealed (自20世纪中期以来，社会学家和传播科学家一直对有影响力的个人的研究感兴趣，这是可以理解的。通过准确识别具有影响力的个人，政策制定者可以在公共卫生和传播有益于社会的创新等关键问题上左右公众舆论。早期研究[27,33,55]调查了大量的人，通常是美国有代表性的中等城市的居民，并询问他们在各个领域（如公共卫生、时尚、政治）向谁咨询建议。这项早期工作揭示了)

  • (i) that within each domain people seek advice from a small group of other individuals (typically around 5), (在每个领域内，人们都会向一小群其他人（通常在5人左右）寻求建议，)
  • (ii) that some key individuals, commonly referred to as opinion leaders, are consistently sought out by others for advice, and therefore exert a much larger influence than others, (一些关键人物，通常被称为意见领袖，总是被其他人寻求建议，因此比其他人发挥更大的影响力，)
  • and (iii) that opinion leaders are domain specific. Although this work revealed that people rely on just a few individuals to inform their opinion, there was no way to evaluate the quality of the decisions that people made. (意见领袖是特定领域的。虽然这项研究表明，人们只依赖少数人来表达自己的意见，但无法评估人们所做决定的质量。)

• (3)With the advent of computational methods, network theory, and the Internet, the research focus shifted to describing networks of social influence and developing methods for leveraging the clout of influential individuals in them [3, 28, 35, 54]. Social networks could be directly reconstructed by observing friendships or follower counts on online websites. Seminal methods for ranking search results, such as PageRank, use a network’s structure to assign value to different sources of information or individuals (e.g., webpages or blogs, see [41]). PageRank’s general approach has been used by social scientists to assign status to different people or sources of information in the offline world. Here, social influence is a consequence of the network’s structure, where well-connected (or well-positioned) individuals are most influential [13, 26]. (随着计算方法、网络理论和互联网的出现，研究重点转向描述具有社会影响力的网络，并开发利用其中有影响力的个人影响力的方法[3,28,35,54]。社交网络可以通过观察在线网站上的友谊或关注人数来直接重建。对搜索结果进行排名的开创性方法，如 PageRank ，使用网络结构为不同的信息源或个人（例如网页或博客，见[41]）分配价值。社会学家使用PageRank的一般方法，在离线世界中为不同的人或信息源分配身份。在这里，社会影响力是网络结构的一个结果，其中关系良好（或位置良好）的个人最具影响力[13,26]。)
  

• (4)Coming to grips with the structure of social influence is crucial for the recommender systems and computational social science communities. Classic collaborative filtering algorithms, such as the weighted k-nearest neighbors algorithm (k-nn), essentially distribute social influence among the individuals in the system’s knowledge base [11]. For each target individual, k-nn pays attention to only a relatively small number of similar others (typically between 10 and 50, see [22, 23])—implying a particular network of social influence [29, 32]. Critically, k-nn can also represent a broad array of decision strategies that have been studied by social and behavioral scientists in offline settings (see Table 1). As in the communities studied by sociologists and communication scientists since the 1950s, the opinions of a few, influential individuals might be consulted more often by recommender systems. Going beyond previous research, we can now uncover the statistical properties of the opinions of the individuals whose advice is sought, and investigate the performance of different social learning strategies. (对于推荐系统和计算社会科学社区来说，掌握社会影响力的结构至关重要。经典的协同过滤算法，如加权k近邻算法（k-nn），本质上是在系统知识库中的个体之间分配社会影响[11]。对于每个目标个体，k-nn只关注相对较少的类似个体（通常在10到50之间，见[22,23]）——这意味着一个特定的社会影响网络[29,32]。关键的是，k-nn还可以代表社会和行为科学家在离线环境中研究过的一系列广泛的决策策略（见表1）。正如自20世纪50年代以来社会学家和传播科学家所研究的社区一样，推荐系统可能会更频繁地咨询少数有影响力的个人的意见。除了之前的研究，我们现在可以发现被征求意见的个人意见的统计特性，并调查不同社会学习策略的表现。)

• (5)Previous research on social influence in recommender systems has focused on two main topics. (之前关于推荐系统中社会影响的研究主要集中在两个主题上。)

  • First, motivated by the threat of malicious attacks on recommender systems (i.e., “shilling attacks”), researchers have developed techniques to identify and avert attackers who want to exploit the system for their own benefit [31, 45, 48]. Bot attacks in which each item is rated by its average score (with some random error added to it), are particularly effective in influencing collaborative filtering recommenders [31]. (首先，出于对推荐系统的恶意攻击（即“先令攻击”）的威胁，研究人员开发了一些技术，以识别并避免攻击者利用该系统谋取自身利益[31,45,48]。在机器人攻击中，每个项目都根据其平均分数进行评级（添加了一些随机错误），这在影响协同过滤推荐方面尤其有效[31]。)
  • Second, researchers have leveraged social influence to design more effective collaborative filtering algorithms or run more cost-efficient marketing campaigns [11, 16, 47]. By studying the structure of social influence, we hope to derive insights into how recommendation algorithms can be further improved and made resilient against attacks. (其次，研究人员利用社会影响力来设计更有效的协同过滤算法，或开展更具成本效益的营销活动[11,16,47]。通过研究社会影响力的结构，我们希望能够深入了解如何进一步改进推荐算法，使其具有抵御攻击的能力。)

• (6)Several questions pertaining to both offline and online opinion spaces remain unaddressed: First, is it possible to identify characteristics (e.g., statistical properties) that reliably predict whether somebody is influential or has the potential to become influential within a domain? Second, how do the recommender algorithms or social learning strategies used determine the distribution of social influence (e.g., varying k in k-nn or the number of people asked for advice offline)? Third, what is the structure of the networks produced by k-nn and the corresponding social learning strategies? In this paper, we investigate these three questions in a diverse set of large- and small-scale datasets. (关于离线和在线意见空间的几个问题仍然没有得到解决：首先，是否有可能确定可靠地预测某人在某个领域是否有影响力或有可能成为有影响力的人的特征（例如统计特性）？第二，所使用的推荐算法或社会学习策略如何决定社会影响的分布（例如，k-nn中的k变化或离线咨询的人数）？第三，k-nn产生的网络结构和相应的社会学习策略是什么？在本文中，我们在一组不同的大型和小型数据集中研究这三个问题。)

2 FRAMEWORK AND METHODS

The simulation framework, results, and the code for visualizing the results are publicly available at https://osf.io/duj8q/.

2.1 Recommendation algorithms

• (1)In our analysis, we rely on the widely used k-nearest neighbors algorithm (k-nn) [15, 44, 46], allowing for differential weights [7]. Such a weighted nearest neighbor algorithm can be expressed as follows: (在我们的分析中，我们依赖于广泛使用的k-最近邻算法（k-nn）[15,44,46]，考虑到不同的权重[7]。这种加权最近邻算法可以表示为：)
  

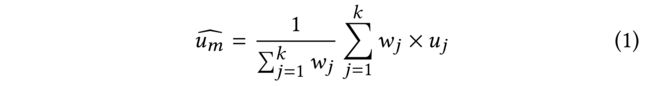
  • where $u_m$ is an individual’s estimate of the utility of an option $m$, (是个人对选项m效用的估计)
  • and $j$ is the $j$th nearest neighbor to the target user. ($j$是目标用户的第$j$个最近邻居。)
  • For $k$ = 1, the algorithm seeks advice from only the most similar other individual. (该算法只向最相似的其他个体寻求建议)
  • Setting $k=N-1$, where $N$ is the total number of people in a dataset, amounts to the weighted averaging strategy. (其中$N$是数据集中的总人数，相当于加权平均策略。)
  • For values of $k$ between these two extremes, we obtain the well-known $k-nn$, but with differential weights. (对于这两个极端之间的$k$值，我们得到了众所周知的$k-nn$，但有不同的权重)

• (2)We used the Pearson correlation coefficient as a measure of similarity ($w$) between two individuals $i$ and $j$ [23], defined as follows: (我们使用皮尔逊相关系数作为两个个体$i$和$j$[23]之间相似性（$w$）的度量，定义如下：)
  

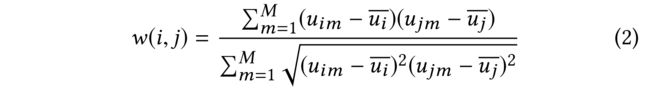
  • where $u_{im}$ is the evaluation that the target individual $i$ gave to item $m$ (是目标个人$i$对项目$m$的评估)
  • and $u_{jm}$ is the evaluation that the $j$th individual gave to the same item $m$. (是第$j$个人对同一物品$m$的评价)
  • $M$ stands for the total number of items. (表示项目总数。)

• (3)We use a similarity sensitivity parameter $\rho$ that allows us to amplify or dampen the weights of different individuals [7, 40]. We directly modify the weights obtained from Eq. 2 using the following scheme: (我们使用了一个相似敏感性参数$\rho$，它允许我们放大或减弱不同个体的权重[7,40]。我们使用以下方案直接修改从等式2获得的权重：)
  

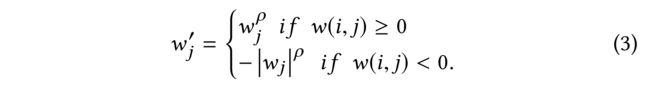
• (4)By varying $k$ and $\rho$, we can produce several collaborative filtering algorithms and social learning and information aggregation strategies studied in the social and behavioral sciences [2]. (通过改变$k$和$\rho$，我们可以产生几种协同过滤算法，以及社会和行为科学[2]研究的社会学习和信息聚合策略。)

  • For instance, setting $\rho =0$ and $k=n$ gives the original formulation of $k-nn$, ($k-nn$的原始公式)
  • while setting $\rho >1$ overweights the opinions of the individuals more similar to the target, as is common in implementations of the weighted nearest neighbors strategy in collaborative filtering [7]. (而设置$\rho >1$会加重与目标更相似的个体的意见，这在协同过滤中的加权最近邻策略实现中很常见[7]。)
  • In Table 1 , we illustrate how different parameterizations of our model map onto different information aggregation strategies. (在表1中，我们说明了模型的不同参数化如何映射到不同的信息聚合策略。)

2.2 The datasets

We analyzed an array of datasets, including

• Jester, a widely studied collaborative filtering dataset on humor collected by Goldberg and colleagues [19]; (Jester是Goldberg及其同事收集的一个广泛研究的关于幽默的协作过滤数据集[19]；)
• datasets on visual art, architecture, and landscapes collected by Vessel and colleagues [53]; (Vesser及其同事收集的视觉艺术、建筑和景观数据集[53]；)
• and data on the attractiveness of people’s faces collected by DeBruine and Jones [10]. (DeBruine和Jones收集的关于人脸吸引力的数据[10]。)
• The Vessel et al. and DeBruine/Jones datasets have the structure of collaborative filtering datasets and represent key domains of interest for the recommender systems community (e.g., real estate, travel, dating). (Vesser等人和DeBruine/Jones数据集具有协同过滤数据集的结构，代表了推荐系统社区感兴趣的关键领域（如房地产、旅游、约会）。)
• Below we specify how the stimuli were selected and describe the study protocols used to elicit the ratings. In the Vessel et al. studies, participants were asked to evaluate the same images on a 7-point scale from “not aesthetically moving” to “very aesthetically moving” two or three times; we used the average evaluation across multiple ratings from the same participant. (下面我们详细说明了如何选择激励，并描述了用于得出评分的研究方案。在Vesser等人的研究中，参与者被要求以7分制对相同的图像进行评估，从“不美的移动”到“非常美的移动”两到三次；我们使用了来自同一参与者的多个评分的平均评价。)
  

Visual art: 24 people evaluated 109 photographs of visual art sourced from the Catalog of Art Images Online (CAMIO) and from museum collections. The collection included lesser-known artwork from a variety of periods, styles, genres, and cultural backgrounds. (24人对109张视觉艺术照片进行了评估，这些照片来源于在线艺术图像目录（CAMIO）和博物馆藏品。该系列包括来自不同时期、风格、流派和文化背景的鲜为人知的艺术品。)

Interior and exterior architecture: 17 people evaluated 118 interior architecture images and 19 people evaluated 108 exterior
architecture images, all of which were chosen to highlight architectural detail. Most of them were selected from ArtStor, an image database that covers many cultures and periods. (室内和室外建筑：17人评估了118张室内建筑图片，19人评估了108张室外建筑图片，所有这些图片都是为了突出建筑细节。其中大部分是从ArtStor中挑选出来的，ArtStor是一个涵盖多种文化和时期的图像数据库。)

Landscapes: 18 people evaluated 148 natural images representing a diverse set of biomes, weather, and views. (景观：18人评估了148幅代表不同生物群落、天气和景观的自然图像。)

Faces: 2,513 people (ages 17–90 years) evaluated the attractiveness of 102 male and female individuals of varying ages and eth-
nic backgrounds on a 1–7 scale ranging from “much less attractive than average” to “much more attractive than average” (see
http://faceresearch.org/). (面孔：2513人（年龄17-90岁）对102名不同年龄和eth-nic背景的男性和女性的吸引力进行了1-7级评估，范围从“远低于平均水平”到“远高于平均水平”（见http://faceresearch.org/).)

Jester jokes: The Jester dataset was collected from April 1999 to May 2003 by an online recommender system that allowed Internet users to read and rate jokes on a scale ranging from “not funny” (−10) to “funny” (+10). Users first evaluated a number of jokes in
random order; the system then recommended jokes from a pool of 100 items until all jokes were presented. For simplicity, we used
only the data from participants who evaluated all jokes (reducing the number of participants from 73,421 to 14,116). (Jester笑话：Jester数据集是由一个在线推荐系统从1999年4月到2003年5月收集的，该系统允许互联网用户阅读笑话，并根据“不好笑”等级别对笑话进行评分(−10） 到“搞笑”（+10）。用户首先以随机顺序评估一些笑话；然后，系统从100个项目中推荐笑话，直到所有笑话都呈现出来。为了简单起见，我们只使用了参与者评估所有笑话的数据（将参与者数量从73421减少到14116）。)

2.3 Performance of k-nn

• For all individuals in the dataset, we calculated the performance of different versions of the weighted k-nearest neighbors algorithm by independently varying the value of k and similarity sensitivity parameter $\rho$. To this end, we assessed the out-of-sample performance of the k-nn algorithm by splitting the data into two equally sized parts: training vs. test sets. We used the training set to estimate the free parameters (i.e., the correlation coefficients between each pair of individuals; see Eq. 2). We then created all possible paired comparisons between two items in the test set and used the correlations obtained from the training set to predict which items people would prefer more strongly (i.e., rate more highly) for each version of (weighted) k-nn (defined by its respective pair of k and ρ).1 For each individual, each version of k-nn, and each dataset, we calculated the proportion of correct predictions across all paired comparisons in the test set. We then averaged the results across 100 simulation repetitions. (对于数据集中的所有个体，我们通过独立改变k值和相似敏感性参数$\rho$来计算不同版本的加权k-最近邻算法的性能。为此，我们通过将数据分成两个大小相等的部分来评估k-nn算法的样本外性能：训练集和测试集。我们使用训练集来估计自由参数（即每对个体之间的相关系数；见等式2）。然后，我们在测试集中的两个项目之间创建了所有可能的配对比较，并使用从训练集中获得的相关性来预测人们对每个版本的（加权）k-nn（由其各自的k和ρ对定义）更强烈（即评分更高）的偏好项目。1 对于每个个体，每个版本的k-nn，对于每个数据集，我们计算了测试集中所有配对比较中正确预测的比例。然后，我们对100次模拟重复的结果进行平均。)

2.4 Reconstructing social influence networks

• For the network analyses, we used the same procedure as described above except that we used all items in a dataset (i.e., no cross validation procedure). We varied the value of $k$ [i.e., 2, 5, 10, and 50] and then constructed advice networks with nodes representing
  the different people in the dataset. While all individuals had by definition the same number of $k$ outgoing edges connecting them to
  other nodes, people could have a varying number of incoming edges depending on how often the recommendation algorithm sought
  their advice for other people. We used node strength, defined as the sum of the absolute weights2assigned to each of the $k$ nearest neighbors, as a measure of social influence that naturally fits the weighted $k-nn$ algorithm and weighted networks more generally [4]. This general approach can be also used with algorithms that calculate similarity between users on a dimensionally reduced space [34] or when using other observable information about individuals to calculate similarity between them [21]. (对于网络分析，我们使用了与上述相同的程序，但我们使用了数据集中的所有项目（即，无交叉验证程序）。我们改变了$k$的值[2,5,10和50]，然后用代表数据集中不同人群的节点构建了建议网络。虽然根据定义，所有个体都有相同数量的$k$传出边将其连接到其他节点，但根据推荐算法为其他人寻求建议的频率，人们可能会有不同数量的传入边。我们使用节点强度（定义为分配给每个$k$近邻的绝对权重之和）作为衡量社会影响力的指标，自然符合加权$k-nn$算法和更一般的加权网络[4]。这种通用方法也可用于在降维空间[34]上计算用户之间相似性的算法，或在使用关于个体的其他可观察信息来计算他们之间的相似性[21]时使用。)

3 RESULTS

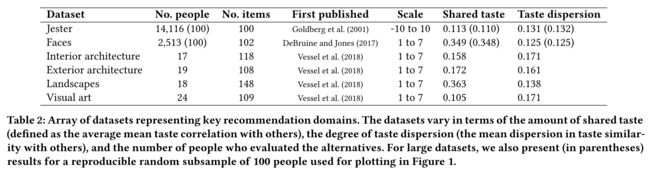
To investigate the relation between the statistical properties of people’s taste and the performance of k-nn, we calculated the mean taste similarity, defined as the (arithmetic) average correlation between each individual’s taste ratings and the ratings of all of their potential peers, and taste dispersion, defined as the standard deviation of those same correlations [2]. In Table 2, we also report the grand mean of those mean taste similarities (referred as shared taste) and taste dispersions for each dataset. Unless otherwise noted, we present results for $\rho =1$. For the Jester and Faces environments, we plot the networks for a subsample of individuals in Figure 1. (为了研究人们口味的统计特性与k-nn性能之间的关系，我们计算了平均口味相似性，定义为每个人的口味评分与其所有潜在同伴的评分之间的（算术）平均相关性，以及味觉分散度，定义为这些相同相关性的标准偏差[2]。在表2中，我们还报告了每个数据集的平均口味相似性（称为共享味觉）和口味分散度的总平均值。除非另有说明，我们给出$\rho =1$的结果。对于Jester和Faces环境，我们在图1中绘制了个人子样本的网络。)

3.1 Who are the most influential individuals?

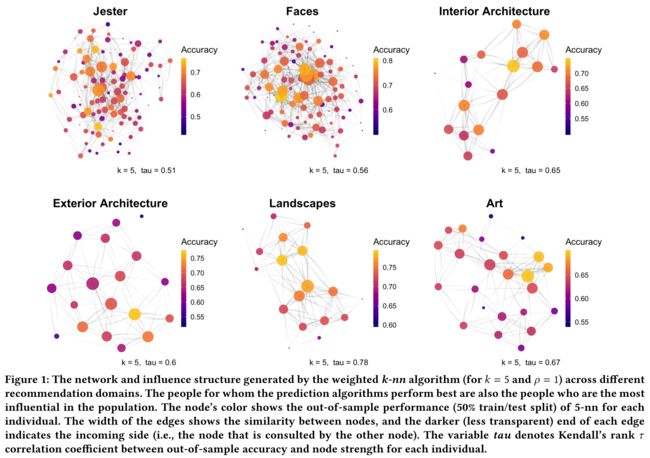
• The most influential individuals are also those who benefit most from weighted $k-nn$’s recommendations; the least influential individuals benefit much less (Figure 1). (最有影响力的个人也是那些从加权$k-nn$推荐中受益最多的人；影响力最小的个人受益要少得多（图1）。)
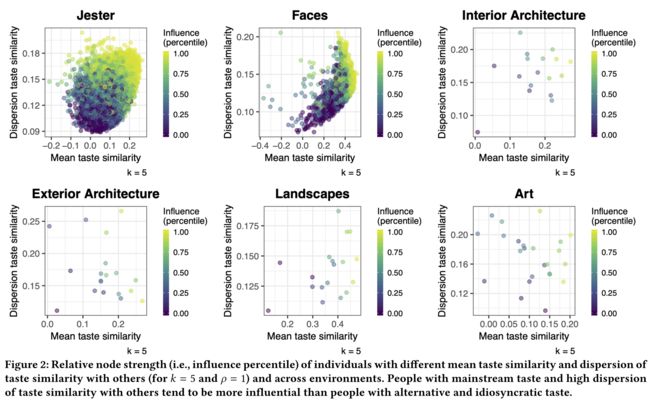
  • To quantify this relationship, we calculated Kendall’s $\tau$ between an agent’s node strength and the predictive out-of-sample performance of the $k-nn$ algorithm for that individual; we found a strong relationship in all datasets (see Figure 1 for the values of τ). The most influential individuals typically have mainstream tastes but also high dispersion in taste similarity with others (Figure 2). These two attributes can be used to directly predict $k-nn$’s performance for different individuals. (为了量化这种关系，我们计算了代理节点强度和对该个体的$k-nn$算法的预测样本外性能之间的Kendall $\tau$；我们在所有数据集中都发现了很强的关系（$\tau$值见图1）。最有影响力的人通常有主流口味，但与其他人的口味相似性也很分散（图2）。这两个属性可用于直接预测k-nnk−nn对不同个体的表现。)
  • For example, when comparing the people with the highest and lowest accuracy in the Jester and Faces datasets, differences can be as large as 30% (see also [2]). When $k=N-1$, the finding that individuals with higher dispersion in taste similarity exert a larger influence follows almost directly from our definition of influence: Their opinions on average correlate more strongly with those of others—either positively or negatively. (例如，在比较Jester和Faces数据集中准确度最高和最低的人时，差异可能高达30%（另见[2]）。当$k=N-1$时口味相似性分散程度越高的个体产生的影响越大，这一发现几乎直接源于我们对影响的定义：他们的观点平均而言与其他人的观点有更强烈的正相关或负相关。)
  • However, this relation is non-trivial for lower values of $k$: As $k$ decreases, people with mainstream taste but low dispersion in taste similarity do not enter the group of consulted individuals as often. They tend to be overshadowed by individuals with slightly higher correlations to the target. (然而，对于$k$值较低的人来说，这种关系并非无关紧要：随着$k$值的降低，具有主流口味但口味相似性分散度较低的人不会经常进入咨询群体。他们往往会被与目标相关度稍高的个体所掩盖。)
    

3.2 Weighting and social influence distribution

• The inequality in social influence stems from two distinct, but mutually compatible, aspects of how weighted $k-nn$ works. (社会影响力的不平等源于$加权k-nn$的两个不同但相互兼容的方面工作。)
  • The first is that unequal weights are assigned to different individuals (Eq. 1). (首先，不同的个体被赋予不同的权重（等式1）。)
  • The second is that—irrespective of any weights—only a few ($k$) individuals are considered. (第二个是，不管权重如何，只考虑少数（k）个个体。)
• For $k=N-1$ and $\rho =1$, the only cause of influence inequality is the simple, proportional weighting (i.e., when $\rho =1$). Even in this case, where the opinion of each individual enters the calculation of recommendations, there is some inherent inequality in people’s clout due to the different extents to which their opinions correlate with those of others. (对于$k=N-1$和$\rho =1$时，影响不平等的唯一原因是简单的比例加权（即当$\rho =1$时）。即使在这种情况下，如果每个人的意见都参与了建议的计算，由于他们的意见与其他人的意见之间的关联程度不同，人们的影响力也存在一些固有的不平等。)
• To quantify this relationship, we calculated the Gini coefficients—a common measure of inequality—for each domain for $k=N-1$ and $\rho =1$. The mean Gini coefficient was 0.23, with the smallest in the landscapes environment (0.13), and the largest in the Jester environment (0.34), indicating that in all domains using the correlations directly as weights produces moderate inequality of social influence. (为了量化这种关系，我们计算了基尼系数，这是k=N的每个域的一个常用不平等性度量$k=N-1$和$\rho =1$。基尼系数的平均值为0.23，在景观环境中最小（0.13），在Jester环境中最大（0.34），这表明在所有领域中，直接使用相关性作为权重会产生适度的社会影响不平等。)
• When $\rho$ is increased, as expected, the Gini coefficient consistently increases as well, producing a mean coefficient across environments of 0.7 for $\rho =10$. Overall, social influence inequality tends to be larger in taste domains with little shared taste. To see this, compare again the Jester environment, which has the second lowest shared taste (shared taste: 0.113, Gini: 0.86) with the Landscapes environment, which has the largest (shared taste: 0.363, Gini: 0.51); this result holds for all values of $\rho$ we investigated. (当$\rho$如预期的那样增加时，基尼系数也会持续增加，当$\rho =10$时，整个环境的平均系数为0.7。总的来说，社会影响不平等往往在没有共同品味的品味领域更大。要了解这一点，请再次比较Jester环境和景观环境，前者的共享品味第二低（共享品味：0.113，基尼：0.86），后者的共享品味最大（共享品味：0.363，基尼：0.51）；这个结果适用于我们研究的所有hoρ值。)

3.3 Attention and social influence distribution

• (1)In many cases, people in real life and recommender systems algorithms do not pay attention to every other individual. There are good reasons for this: focusing on a subset of people, rather than taking everybody’s opinion into account, can lead to better predictive performance [23, 51]. In addition, paying attention to fewer “advisers” can reduce the effort of actively collecting and aggregating information. In other words, even if paying attention to everybody actually improved predictive performance, it may still make sense for people to pay attention to just a few individuals. Our results show that limiting attention to a few similar others can lead to substantial influence inequality. This can be seen by comparing the average Gini coefficient across environments. In the baseline case where $k=5$ and $\rho =1$ (see Figure 1), the mean Gini coefficient is 0.43, which reflects substantial inequality. Influence inequality further increases as the number of individuals to which people or algorithms pay attention decreases. (在许多情况下，现实生活中的人们和推荐系统的算法并不关注其他每一个人。这有很好的理由：关注一部分人，而不是考虑每个人的意见，可以带来更好的预测性能[23,51]。此外，关注较少的“顾问”可以减少积极收集和汇总信息的工作量。换句话说，即使关注每个人实际上提高了预测性能，人们关注少数人可能仍然是有意义的。我们的研究结果表明，将注意力限制在少数类似的人身上可能会对不平等产生重大影响。通过比较不同环境下的平均基尼系数可以看出这一点。在k=5和ρ=1的基线情况下（见图1），基尼系数的平均值为0.43，这反映了实质性的不平等。随着人们或算法关注的个体数量减少，影响力不平等进一步加剧。)
• (2)For example, when $k$ = 2, that is, an individual or algorithm consults only two other people, the influence distributions become even more unequal with a mean Gini coefficient of 0.53. For small values of k, the distribution of social influence is more unequal in environments where people have high levels of shared tastes—the inverse of high $\rho$ values. This can be seen by comparing the landscapes environment with the art environment (Figure 1, Gini 0.43 vs 0.30, respectively, for k = 5), or the faces environment with the Jester environment (Figure 3, Gini 0.67 vs. 0.62, respectively, for k = 5) . (例如，当k=2时，也就是说，一个人或算法只咨询另外两个人，影响分布变得更加不平等，平均基尼系数为0.53。对于较小的k值，在人们有较高共享品味的环境中，社会影响力的分布更不平等，而高$\rho$值正好相反。这可以通过比较风景环境和艺术环境（图1，基尼0.43对0.30，k=5）或faces环境和Jester环境（图3，基尼0.67对0.62，k=5）来看出。)
  

3.4 Resulting network structures

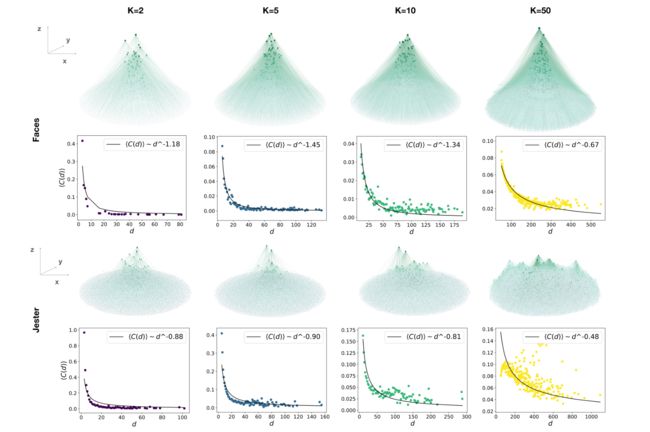
• To shed more light on the social networks that emerge from k-nn, we focused on Jester and Faces, the two large datasets in our collection, and examined the simple case of an unweighted k-nn algorithm (ρ = 0). (为了进一步了解k-nn产生的社交网络，我们将重点放在Jester和Faces上，这是我们收集的两个大型数据集，并研究了未加权k-nn算法（ρ=0）的简单情况。)
• In this case, node strength reduces to in-degree, the arguably most basic centrality measure. In our setting, in-degree represents the number of times a node (person) was sought for advice (or involved in the calculation of a recommendation). The analysis shows that in-degree varies greatly across people: For a wide range of values of $k$ there are only a few influential individuals (hubs; see Figure 3). (在这种情况下，节点强度降低到可以说是最基本的中心性度量。在我们的设置中，in-degree表示节点（人员）寻求建议（或参与建议计算）的次数。分析表明，不同的人在程度上差异很大：对于$k$值的广泛范围，只有少数有影响力的人（枢纽；见图3）。)
• A second metric, the local clustering coefficient— which measures the extent to which an individual’s advisers also advise each other—is inversely related to the in-degree following the power law $C(d)=d^{-\beta }$: the less influence individuals exert over others, the tighter the clusters they tend to form (see scatter plots and fit in Fig. 3). This exact relation is predicted by the hierarchical network model [43] and cannot be accounted for by other scale-free network models. This relation is stable over a wide range of values of k in both datasets; it is only lost in the Jester dataset for very large values of $k$. (第二个指标是局部聚集系数，它衡量个人顾问之间相互建议的程度，与幂律$C(d)=d^{-\beta }$的程度成反比：个人对他人施加的影响越小，他们倾向于形成的集群就越紧密（参见散点图和图3中的拟合）。这种精确的关系由分层网络模型[43]预测，不能由其他无标度网络模型解释。这一关系在两个数据集中的k值范围内都是稳定的；它只在Jester数据集中丢失了非常大的$k$值。)

4 GENERAL DISCUSSION AND CONCLUSION

• (1)Roger Ebert is probably the most famous film critic in the history of film-making. His opinion was sought by scores of movie-goers and a website bearing his name is still active. But was there something special about Ebert’s opinions that made him a nationwide phenomenon in the United States and source of advice for so many people? Are there people like Ebert in recommender systems? And is it possible to identify them solely on the basis of the statistical properties of their tastes? (罗杰·埃伯特可能是电影制作史上最著名的影评人。数十名电影观众征求了他的意见，一个以他的名字命名的网站仍在活跃。但埃伯特的观点是否有什么特别之处，使他在美国成为一个全国性的现象，并为这么多人提供建议？在推荐系统中有像埃伯特这样的人吗？有没有可能仅仅根据它们的口味的统计特性来识别它们？)

• (2)Our work looks at social influence in recommender systems through the lens of network theory. Hitherto, the recommender systems community has used social networks primarily as an additional source of information [18, 37, 50], and used network theory more broadly to visualize recommender systems as bipartite user-item networks (see, e.g., [57]). Here, extending early work by Lathia et al. [32], we investigated the social networks of influence produced by the weighted k-nearest neighbors algorithm (k-nn).We found that skewed social influence distributions are inherent in recommender systems and that the emerging networks are hierarchically organized. The most influential individuals (sitting on top of the hierarchies) tend to be those who benefit the most from the k-nn algorithm. (我们的工作通过网络理论的视角来研究推荐系统中的社会影响。迄今为止，推荐系统社区主要使用社交网络作为额外的信息来源[18,37,50]，并更广泛地使用网络理论将推荐系统可视化为两部分用户项网络（参见，例如[57]）。在这里，我们扩展了Lathia等人[32]的早期工作，研究了加权k-最近邻算法（k-nn）产生的影响的社会网络。我们发现，倾斜的社会影响力分布在推荐系统中是固有的，新兴网络是分层组织的。最有影响力的个人（坐在层次结构的顶端）往往是那些从k-nn算法中受益最多的人。)

• (3)Previous research showed that malicious individuals can game recommender algorithms by designing bots that evaluate options in a way that makes the evaluations appear informative to many similar others [31,45,48]. Our results provide an explanation for the efficiency of averaging attacks on collaborative filtering algorithms (i.e., rating each item by its average and adding some noise). Rating profiles using averaging schemes score very high, in terms of both mean taste correlation and often also dispersion of taste similarity with the crowd. If such an individual actually existed, they would be among the most influential in the settings we studied and would benefit a lot from recommendations. More broadly, our results show that it is possible to consistently identify individuals who are more likely to become influential by looking at the statistical properties of their taste. (之前的研究表明，恶意个人可以通过设计机器人来对选项进行评估，从而让评估结果对许多类似的人来说都是有用的[31,45,48]。我们的结果解释了平均攻击协同过滤算法的效率（即，根据每个项目的平均值对其进行评级，并添加一些噪声）。在平均味觉相关性和味觉相似性在人群中的分散性方面，使用平均方案的评分模式得分非常高。如果真的存在这样一个人，他们将是我们研究的环境中最有影响力的人之一，并将从建议中受益匪浅。更广泛地说，我们的结果表明，通过观察个人品味的统计特性，可以始终如一地识别出更有可能成为有影响力的人。)
  
  

• (4)The k-nn algorithm and its capacity to emulate different social learning strategies provides a fresh way to look at networks of social influence in the offline world. (k-nn算法及其模拟不同社会学习策略的能力为研究离线世界中的社会影响力网络提供了一种新的方法。)

  • For example, our analysis points to a simple yet plausible process by which homophily [38] and opinion leaders [27] might emerge in real-world networks: People can learn more by connecting to people who are similar to them and fare better if they limit their attention to just a few similar others. (例如，我们的分析指出了一个简单但似乎合理的过程，通过这个过程，现实世界中的人际网络中可能会出现嗜同性[38]和意见领袖[27]：人们可以通过与他们相似的人建立联系学到更多，如果他们将注意力限制在少数几个相似的人身上，情况会更好)
  • The relationship between in-degree and clustering coefficient we identified is a property of many real-world networks (e.g., the WWW or protein-interaction networks; see [52]) and we found that such a network structure can also emerge when recommendation algorithms (like k-nn) create links from pairwise similarities in people’s tastes. Some networks observed in the offline world may have emerged from mechanisms akin to those we described here—further amplified or dampened by cognitive or physical limitations that people experience offline (e.g., limitations in the size of the social network they can maintain [12] or in how sensitive they are to differences in similarity [49]). (我们确定的in-degree和聚类系数之间的关系是许多现实世界网络（如WWW或蛋白质相互作用网络；见[52]）的一个特性，我们发现，当推荐算法（如k-nn）从人们口味的成对相似性中创建链接时，也会出现这种网络结构。在离线世界中观察到的一些网络可能来自与我们在这里描述的机制类似的机制，人们在离线时经历的认知或身体限制进一步放大或减弱了这些机制（例如，他们可以维持的社交网络的规模[12]或他们对相似性差异的敏感程度[49]）。)

• Taken together, our results show that it is possible to analyze recommender systems algorithms and their consequences at both the individual and aggregate level. (综上所述，我们的结果表明，在个体和群体层面上分析推荐系统算法及其后果是可能的。)

  • The data of each individual can be seen as a unique environment with its own statistical properties, nested within a larger overarching data structure. (每个人的数据都可以被视为一个独特的环境，具有自己的统计特性，嵌套在一个更大的总体数据结构中。)
  • Understanding how the data from different individuals create structure can help us unpack the workings of recommendation algorithms and lead to the development of better and more robust recommender systems. (了解来自不同个体的数据是如何创建结构的，可以帮助我们解开推荐算法的工作原理，从而开发出更好、更健壮的推荐系统。)

ACKNOWLEDGMENTS

REFERENCES