深度学习中Transformer的原理和方法(李宏毅视频课笔记)
文章目录
- 0 前言
- 1 RNN to CNN
- 2 Self-Attention
-
- 2.1 Base Method
- 2.2 Matrix Representation
- 2.3 Multi-head Self-attention
- 2.4 Positional Encoding
- 3 Seq2Seq Based on Self-Attention
-
- 3.1 Base Method
- 3.2 Transformer
- 4 Attention Visualization
0 前言
本节学习的是Transformer。Google于2017年6月发布在arxiv上的一篇文章《Attention is all you need》,提出解决sequence to sequence问题的transformer模型,用全self-attention的结构代替了lstm,这也是现在主流的BERT模型的基础。本文由整理李宏毅老师视频课笔记和个人理解所得,详细讲述了Transformer的原理及实现方法。我会及时回复评论区的问题,如果觉得本文有帮助欢迎点赞 。
1 RNN to CNN
一般常用的就是RNN,输入是一串Vector Sequence,输出也是一串Vector Sequence。RNN常用于处理输入是有序的情况,但是RNN有问题——不易被平行化(并行运算)。如图,就单向RNN而言,当仅需要输出 b 4 b^4 b4时,则需要等候 a 1 , a 2 , a 3 , a 4 a^1, a^2, a^3, a^4 a1,a2,a3,a4的输入。即使是双向的RNN, b 1 , b 2 , b 3 , b 4 b^1, b^2, b^3, b^4 b1,b2,b3,b4也不能同时计算:

所以有人想使用CNN来代替RNN,输入不变,三角形代表是一个Filter(不止一个),以3个向量为一组进行扫描。多使用几组Filter也可以做到,输入是一个Sequence,对应输出是一个Sequence:
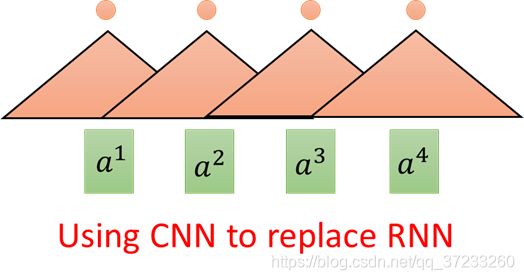
表面上CNN和RNN一样,但是一层CNN的一个输出只考虑三个输入的Vector,但是RNN(双向的)却要考虑整个句子。所以考虑增加CNN的层数,这样就是可以使得感受野增大,即可以考虑所有的输入。CNN的好处是可以平行化,每一个Filter(三角形)都可以单独运算,并不需要等之前或者之后的Filter计算结束。

2 Self-Attention
2.1 Base Method
CNN需要叠很多层,如果只要求一层就要获得所有输入的信息怎么做呢?这里就是引入Self-Attention Layer,可以完美替代双向RNN:

输入是 x i x^i xi,通过一个embedding(映射)W矩阵得到 a i a^i ai,然后将 a i a^i ai输入到self-attention layer,分别乘上三个不同的变换,获得三个不同的vector,即 q i , k i , v i q^i,k^i,v^i qi,ki,vi,代表不同的三种意思:
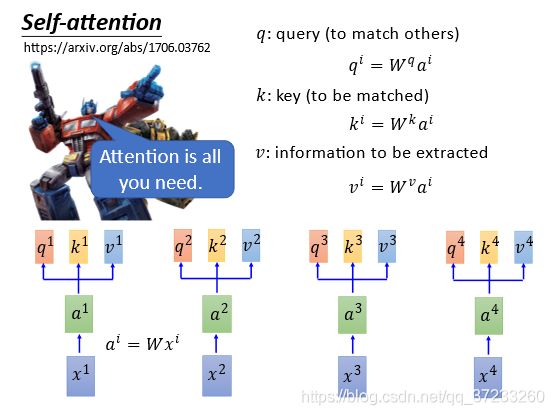
接下来要做拿每一个query q q q去对每一个key k k k做attention(4对4),以 q 1 q^1 q1为例,如下图,得到4个attention: 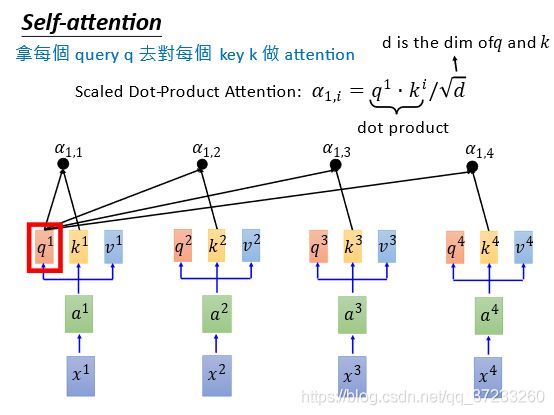
我们已知attention的本质就是匹配度,那么就需要定义匹配度的计算:
α 1 , i = q 1 ⋅ k i / d \alpha_{1, i}=q^{1} \cdot k^{i} / \sqrt{d} α1,i=q1⋅ki/d
其中d是 q q q和 k k k的维度。关于除以 d \sqrt{d} d有个这样的解释: q q q和 k k k的内积的值和维度d大小关系很大,这样除了之后方差就会为1了。当然定义别的匹配度也可以。
接下来通过一个Softmax Layer得到对应的概率值 α ^ 1 , 1 α ^ 1 , 2 α ^ 1 , 3 α ^ 1 , 4 \begin{array}{llll}\hat{\alpha}_{1,1} & \hat{\alpha}_{1,2} & \hat{\alpha}_{1,3} & \hat{\alpha}_{1,4}\end{array} α^1,1α^1,2α^1,3α^1,4:
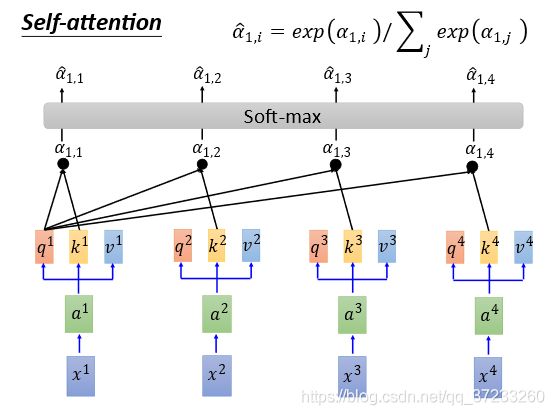
将 α ^ 1 , 1 α ^ 1 , 2 α ^ 1 , 3 α ^ 1 , 4 \begin{array}{llll}\hat{\alpha}_{1,1} & \hat{\alpha}_{1,2} & \hat{\alpha}_{1,3} & \hat{\alpha}_{1,4}\end{array} α^1,1α^1,2α^1,3α^1,4与各自的 v v v相乘之后相加( b 1 = ∑ i α ^ 1 , i v i b^{1}=\sum_{i} \hat{\alpha}_{1, i} v^{i} b1=∑iα^1,ivi 等价于weight sum),得到一个向量 b 1 b^1 b1:
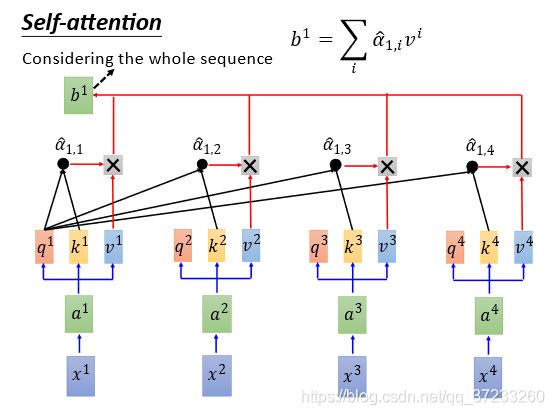
这样Self-Attention就输出一个vector,而且产生这个 b 1 b^1 b1已经考虑了所有输入的信息,如果只想考虑local的信息,只需要将 α ^ 1 , 1 α ^ 1 , 2 α ^ 1 , 3 α ^ 1 , 4 \begin{array}{llll}\hat{\alpha}_{1,1} & \hat{\alpha}_{1,2} & \hat{\alpha}_{1,3} & \hat{\alpha}_{1,4}\end{array} α^1,1α^1,2α^1,3α^1,4中不需要的变成0就可以了。需要什么信息,就获取什么信息。
因为信息是已知的,在同一个时间如下图可以计算 b 2 b^2 b2,并不冲突:
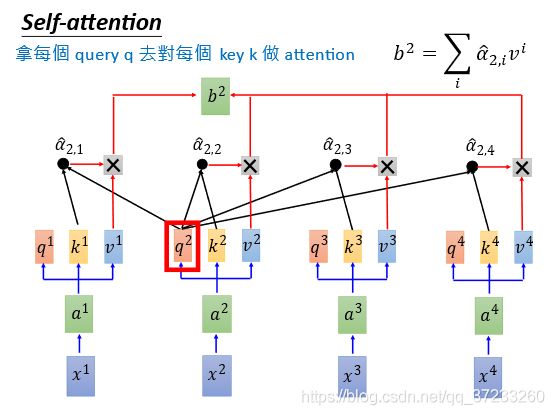
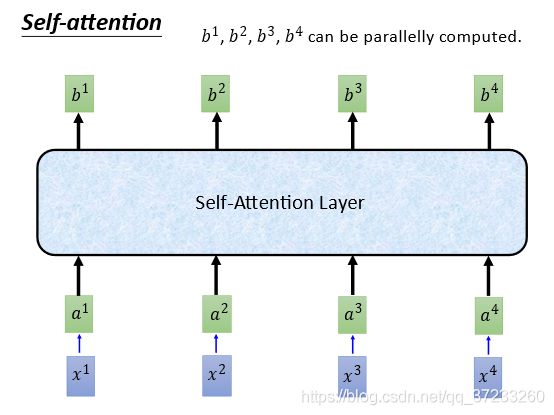
总而言之,输入了 x 1 , x 2 , x 3 , x 4 x^1, x^2, x^3 ,x^4 x1,x2,x3,x4,输出了 b 1 , b 2 , b 3 , b 4 b^1, b^2, b^3, b^4 b1,b2,b3,b4,和RNN做了一样的工作,但是可以平行计算的:
2.2 Matrix Representation
接下来用矩阵的形式表述Self-Attention是怎么做平行化的。将所有的 q q q收集起来作为一个 Q Q Q矩阵,每一列作为一个 q q q,同理可以得到其他的矩阵:
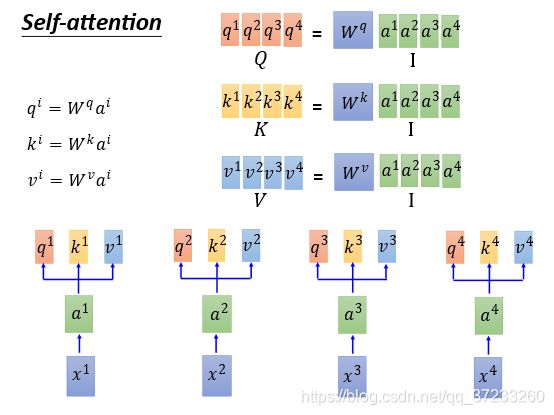
接下来表述 α i , j \alpha_{i,j} αi,j(注意还没有经过Softmax层)的计算。单独的一个 α 1 , 1 \alpha_{1,1} α1,1等于 k 1 k^1 k1的转置乘上 q 1 q^1 q1,为了方便表述先忽略系数 d \sqrt{d} d,将4个都合并起来可以得到:
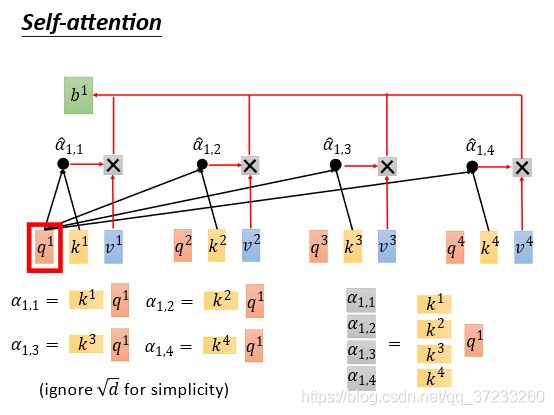
将所有的 α i , j \alpha_{i,j} αi,j合并为一个矩阵,可以得到 A = K T Q A=K^TQ A=KTQ,经过softmax层后得到 A / h a t A^/hat A/hat:
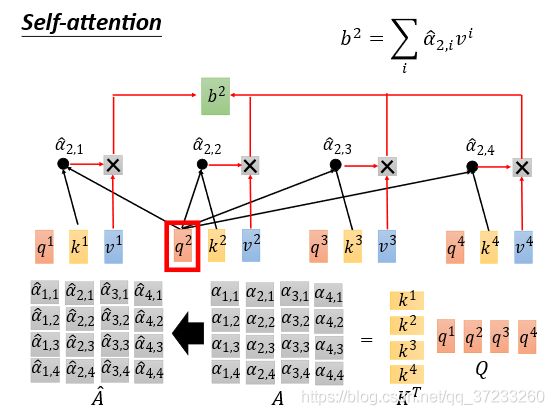
然后表示weight sum,就是self-attention的输出:

2.3 Multi-head Self-attention
Multi-head Self-attention,首先使用2 head的情况举例。每一组的 q I , k I , v i q^I, k^I, v^i qI,kI,vi都分别分裂为两个。但是对应的下标 q , k , v q, k, v q,k,v还是去找其他相同位置的 q , k , v q, k, v q,k,v运算,如图:

通过矩阵拼接可求出 b i b^i bi,也可以使用一个 W 0 W^0 W0获得一个降维的 b i b^i bi:
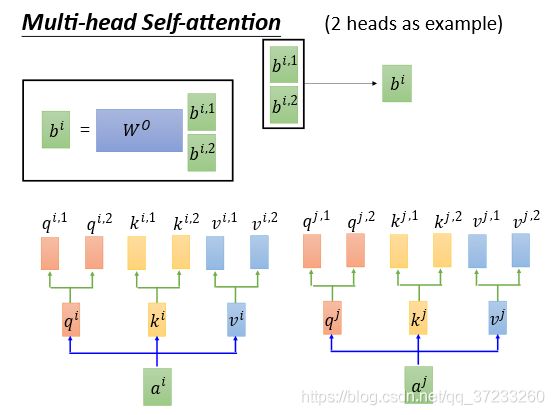
实际在做的时候head的个数是可以调整的。
2.4 Positional Encoding
对于一般的self-attention来说,input的顺序和位置是不重要的,因为做attention的时候所有的输入都会用到,但是这样就少了位置信息。为了解决这个问题,就在 a i a^i ai旁边加上位置向量 e i e^i ei,这两个vector的维度是一样的。这个 e i e^i ei不是学出来的,而是超参数:

为什么是相加而不是接起来呢?这里李宏毅老师给出了一个解释:将每个原始输入 x i x^i xi下面接上一个表征位置信息的独热向量 p i p^i pi,相接的结果乘上一个变换矩阵W,这里的W可以拆解为 W I W^I WI和 W P W^P WP,最后的结果仍然是 a i + e i a^i+e^i ai+ei:
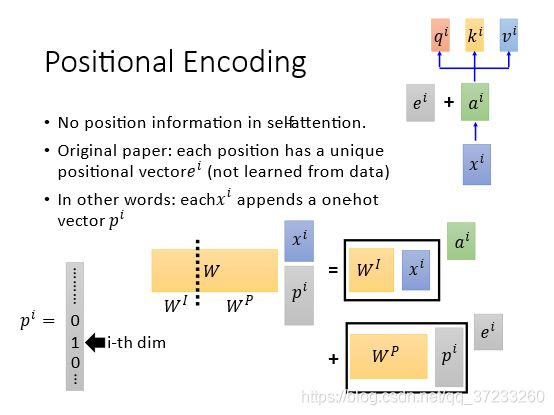
W I W^I WI部分(类似之前的 W W W)和 x i x^i xi相乘得到了 a i a^i ai, W P W^P WP和 p i p^i pi相乘得到了 e i e^i ei。这个 W P W^P WP是可以学习的,不过最好是手动设置的,一般依据的 W P W^P WP画图出来是下面的样子:

3 Seq2Seq Based on Self-Attention
3.1 Base Method
Self-Attention在Seq2Seq模型里是怎么使用的?RNN实现Seq2Seq模型我们已经知道了,一个是Encoder,另外一边是Decoder,可以用来比如训练一个翻译器之类的:
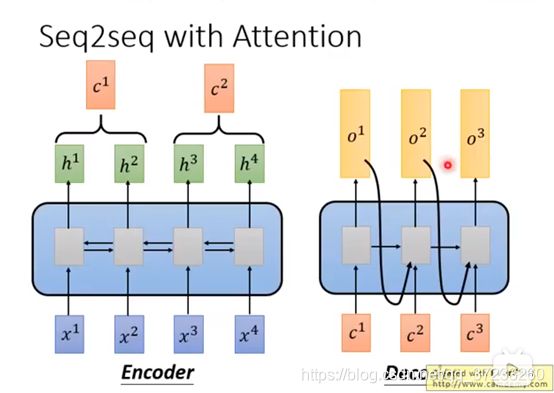
这里的双向的RNN和Decoder的RNN都可以用self-attention替换: 
下图是谷歌制作的self-attention的Encoder和Decoder的运行流程:

3.2 Transformer
这个图是Transformer的模型。输入是“机器学习“,输出是”machine learning“:
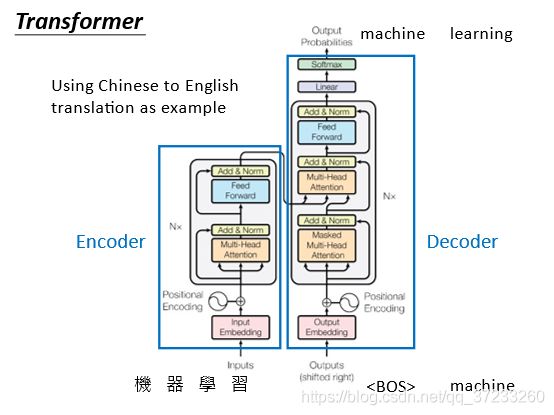
1)先看Encoder的部分。输入input x i x^i xi经过一个embedding 提取特征之后变成之前的 a i a^i ai,然后与位置编码 p i p^i pi在这里加入,会进入灰色的框中。再输入到一个self-attention layer中,输出 b b b之后,经过Add & Norm layer,这个层就是将 b b b和self-attention layer的输入会加起来,加起来之后做一个Layer normalization,可以简单理解为做一个标准化。Feed forward 层可以弥补self-attention的非线性(这里不展开)。
2)再看Decoder部分。Input部分是前一个time step产生的output。这里的第一层是一个叫带masked 的self-attention layer,masked意识是做attention的时候只会关注到已经产生的sequence。然后和Encoder的输出一起做Attention。接下来经过一系列变换后输出:
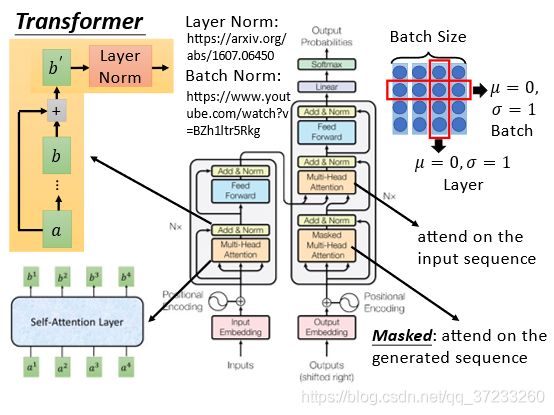
以上就是完整的Transformer的流程。
4 Attention Visualization
将self-attention的结果做可视化操作。当结尾的单词是“tired“时,”it“ attend 更多的是”animal“;如右边的图,当结尾单词是”wide“的时候,”it“ attend 更多的是”street“。

而对于Multi-head Attention来说,一个word可以attend更多的其他词汇:
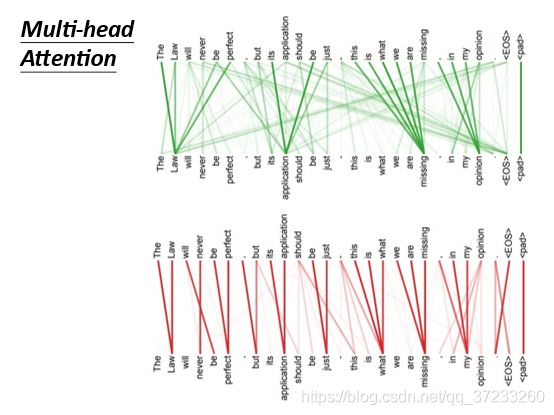
输入一个文章集合,使用transformer生成一篇文章:

在深度上使用RNN的原理将transformer叠加:
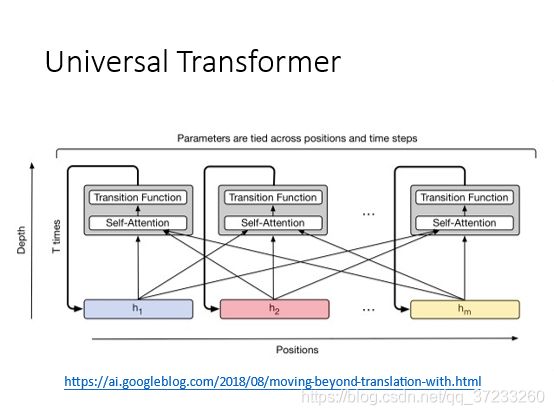
Self-Attention GAN
大意是图像处理时为了获得更多的图像信息,也可以使用Self-Attention: