Learning Affinity from Attention End-to-End Weakly-Supervised Semantic Segmentation withTransformers
Learning Affinity from Attention: End-to-End Weakly-Supervised Semantic Segmentation with Transformers
来源:CVPR 2022,武汉大学、京东、悉尼大学
导言
本文是一篇做自然图像弱监督语义分割的论文,利用图像级的类别标签来实现像素级的语义分割。文中方法采用了基于transformer模块作为骨干网络,利用分类网络各类别对应的CAM作为初始伪标签,同时利用backbone总transformer的多头自注意力(MHSA)的特征得到亲和度图(AFA),结合AFA和random walk方法,并采用像素自适应增强模块(PAR),进一步提升了伪标签质量,作为分割网络的监督信号。实验表明,本文所提方法显著优于近期基于端到端(end-to-end)方法和基于多阶段(multi-stage)方法。论文收录于CVPR 2022,论文地址为:[2203.02664] Learning Affinity from Attention: End-to-End Weakly-Supervised Semantic Segmentation with Transformers (arxiv.org),代码地址为:https://github.com/rulixiang/afa
Abstract
神经网络需要大量训练数据,在语义分割(Semantic Segmentation,简称SS)任务中,fully-supervised方法通常需要大量pixel-level标注,这些标注是labour intensive,成本巨大、代价高昂且耗时耗力。针对这个问题,利用标注成本较低的weak/cheap标注数据(例如image-level、points、bounding box等)的Weakly-supervised SS(简称WSSS)方法吸引了研究人员的广泛关注。文章所提方法属于weakly-supervised范畴,仅仅利用了image-level的标注。受Transformer中self-attention和semantic affinity(语义亲和度)两者间的内在的一致性启发,本文提出了一种…。实验表明,本文所提方法在PASCAL VOC 2012和MS COCO 2014数据集上分别达到66.0%和38.9%的mIoU,显著优于近期基于端到端(end-to-end)方法和基于多阶段(multi-stage)方法。
Introduction
a. 对任务背景的概述
对任务的描述
语义分割的目标是给图像中的每一个像素点分配一个类别标签,从而形成了对整张图像的语义划分。它是计算机视觉的基础任务。
任务难点
由于神经网络需要大量训练数据的特性,fully-supervised方法通常需要大量pixel-level标注,这些标注是labour intensive,成本巨大、代价高昂且耗时耗力。
已有的一些解决方法
利用一些weak/cheap的标注,主要的方法有:
- image-level labels
- points
- scribbles
- bounding boxes
本文方法属于weakly-supervised方法,仅仅利用了image-level的标注。
b. 研究现状
第一阶段 ,基于image-level的WSSS方法通常采用多阶段的框架(multi-stage framework)。不足:这种方法需要训练多个网络,或者多次训练网络,整个训练流程的效率低。
- 首先训练得到一个分类网络,
- 利用分类网络得到类别激活图CAM作为初始伪标签(并非直接就作为label)
- 对得到的CAM进行refinement,作为训练分割网络的label
- 利用supervised方法训练得到一个分割模型
第二阶段,为了避免一阶段存在的不足,很多end-to-end方法被提出。不足:大多利用卷积网络,卷积网络存在对全局特征提取以及全局特征间联系获取能力不足的固有缺陷,这种global relation对于获取整体的激活区域(activating integral object regoin)是至关重要的。如figure 2(a)种所示,CNN-based模型获取到的CAM,只是在一些discriminative的区域较为显著,在目标激活的完整度上是不够的
第三阶段,transformer是个好东西,它的提出,有效解决了卷积网络获取global relation的不足,在多个视觉任务上都取得了重大突破。但是直接利用基于transformer-based的方法得到的CAM作为affinity,仍然是不准确,不完整的。不足:即使是
本文的贡献
- 提出了端到端的、只利用图像级标签的、基于Transformer的 弱监督语义分割框架
- 提出了 Affinity from Attention (AFA) 模块,用于从Transformer的多头自注意力(MHSA)中学得语义亲和度(semantic affinity)的信息,用于 propagate (传播/扩散/生长)伪标签(pseudo label)
- 提出了 Pixel-Adaptive Refinement (PAR) 模块,用于 incorporate (合并/混合)图像的颜色信息(RGB)和空间信息(像素坐标),用于优化伪标签
方法 Methodology
模型整体结构
1. 引入 transformer backbone
一张输入图像首先呗划分为 h × w h \times w h×w 个patches, 这里每一个patch被展平并且经过线性投影从而形成 h × w h \times w h×w 个tokens。
2. CAM 生成以及初始伪标签生成
2.1 CAM生成
Transformer作为编码器,每幅输入的图像都会对应一组它输出的特征图 F ∈ R h w × d F \in \mathbb{R}^{h w \times d} F∈Rhw×d ,这里 d d d 指特征维度。对于给定的类别 c c c,它的类激活图 M c M^c Mc 计算方法由文中公式2给出:
M c = ReLu ( ∑ i = 1 d W i , c F i ) M^{c}=\operatorname{ReLu}\left(\sum_{i=1}^{d} W^{i, c} F^{i}\right) Mc=ReLu(i=1∑dWi,cFi)
这里 R e L U ReLU ReLU 用来移除负激活。最后会用类似GradCAM那样将 M c M^c Mc 缩放到[0,1]。
2.2 初始伪标签 initial pseudo label
论文所给代码中伪标签的生成有两种可选方案。方案一,文中仅设置一个背景区域的阈值 β b \beta_b βb,在CAM中,数值小于 β b \beta_b βb 的位置赋值为 0,反之,赋值 1。
方案二设置了两个超参数 β l \beta_l βl 和 β h \beta_h βh (这里 0 < β l < β h < 1 0 < \beta_l < \beta_h < 1 0<βl<βh<1 )用来将CAM分为可信背景区域、不确定区域和可信前景区域,具体步骤如原文公式4:
Y p i , j = { argmax ( M i , j , : ) , if max ( M i , j , : ) ≥ β h , 0 , if max ( M i , j , : ) ≤ β l , 255 , otherwise Y_{p}^{i, j}=\left\{\begin{array}{lr} \operatorname{argmax}\left(M^{i, j,:}\right), & \text { if } \max \left(M^{i, j,:}\right) \geq \beta_{h}, \\ 0, & \text { if } \max \left(M^{i, j,:}\right) \leq \beta_{l}, \\ 255, & \text { otherwise } \end{array}\right. Ypi,j=⎩⎨⎧argmax(Mi,j,:),0,255, if max(Mi,j,:)≥βh, if max(Mi,j,:)≤βl, otherwise
3. Affinity from Attention (AFA) 和AFA监督信号的生成
3.1 AFA 生成
在transformer中,多头注意力MHSA可表示为: S ∈ R h w × h w × n S \in \mathbb{R}^{h w \times h w \times n} S∈Rhw×hw×n ,其中 h w hw hw 是展平的空间尺寸, n n n 是注意力头的数量。如文章中所说:多头注意力可以看作是有向图,但图像区域之间的亲和度应该是相互对称的。所以这里采用了原注意力矩阵和其自身的转置相加的处理方式来获得对称的注意力矩阵,记为 ( S + S T ) (S+S^T) (S+ST) ,在本文中,AFA 模块通过直接对MHSA进行线性组合,得到亲和度图。具体的步骤文中公式3:
A = M L P ( S + S T ) A = MLP(S + S^T) A=MLP(S+ST)
3.1. AFA监督信号的生成
上面提到的亲和度矩阵缺少对应的标签来监督这个过程,如图3所示,文中AFA监督信号 Y a f f Y_{aff} Yaff由初始化的伪标签,经过PAR模块做优化得到 Y p Y_p Yp,然后按照一定的规则生成亲和度矩阵的标签 Y a f f Y_{aff} Yaff。具体步骤如下:
伪标签转亲和度矩阵标签的过程和 IRNet 中的一处做法类似。 Y p Y_p Yp 取值为 255 的区域代表不确定区域,剩余区域代表确定区域。其中确定区域又分为取值为0的背景区域,和取值为各个类别标签数值的前景区域。对于每个位置,都把它半径 r r r 以内的区域视为邻域,然后分析它与邻域的关系。假设已知某个位置为 i i i,它的一个邻域为 j j j ,规则描述如下:
- 如果 i,j 都是确定区域
- 如果 Y p i Y_{p}^{i} Ypi 和 Y p i j Y_{p}^{ij} Ypij 取值相同,则 Y a f f i , j Y_{aff}^{i,j} Yaffi,j 置为 1,同时位置 i , j i,j i,j 记为positive位置对;
- 如果 Y p i Y_{p}^{i} Ypi 和 Y p j Y_{p}^{j} Ypj 取值不相同,则 Y a f f i , j Y_{aff}^{i,j} Yaffi,j 置为 0,同时位置 i , j i,j i,j 记为negative位置对;
- 如果 i i i 或 j j j 任意一方为不确定区域,则 Y a f f i , j Y_{aff}^{i,j} Yaffi,j 置为 255,表示“忽略”
- 此外,邻域外的关系均置为 255,且 Y a f f i , j Y_{aff}^{i,j} Yaffi,j 和 Y a f f j , i Y_{aff}^{j,i} Yaffj,i 取值相同。
按照上述规则就能得到亲和度矩阵的标签 Y a f f ∈ R h w × h w Y_{aff} \in \mathbb{R}^{h w \times h w} Yaff∈Rhw×hw
4 最终伪标签生成
4.1 伪标签扩散传播 pseudo label propagation
参考IRNet[3]使用随机游走算法(Random Walk)对初始伪标签进行扩散传播。具体步骤如下:
- 先对亲和度矩阵 A ∈ R h w × h w A \in \mathbb{R}^{h w \times h w} A∈Rhw×hw 做处理,求矩阵的 α \alpha α 次方,得到 A α A^{\alpha} Aα,这里 α > 1 \alpha > 1 α>1 时,将削弱亲和度矩阵中小数值的影响
- 对 A α A^{\alpha} Aα进行逐行求和,然后进行行内归一化,得到 T T T
- 然后将 T T T和向量化的CAM矩阵 M ∈ R h × w × c M \in \mathbb{R}^{h \times w \times c} M∈Rh×w×c 相乘,得到处理后的CAM矩阵 M a f f M_{aff} Maff
PAR模块对伪标签的优化
本文PAR的提出收到了其他两篇文章的启发,利用pixel-adaptive convolution来提取RGB以及空间信息,将两者结合得到low-level pairwise affinity。具体步骤如公式8-10
公式8:
κ r g b i j , k l = − ( ∣ I i j − I k l ∣ w 1 σ r g b i j ) 2 , κ p o s i j , k l = − ( ∣ P i j − P k l ∣ w 2 σ pos i j ) 2 \kappa_{r g b}^{i j, k l}=-\left(\frac{\left|I_{i j}-I_{k l}\right|}{w_{1} \sigma_{r g b}^{i j}}\right)^{2}, \quad \kappa_{p o s}^{i j, k l}=-\left(\frac{\left|P_{i j}-P_{k l}\right|}{w_{2} \sigma_{\text {pos }}^{i j}}\right)^{2} κrgbij,kl=−(w1σrgbij∣Iij−Ikl∣)2,κposij,kl=−(w2σpos ij∣Pij−Pkl∣)2
公式9:
κ i j , k l = exp ( κ r g b i j , k l ) ∑ ( x , y ) exp ( κ r g b i j , x y ) + w 3 exp ( κ pos i j , k l ) ∑ ( x , y ) exp ( κ pos i j , x y ) , \kappa^{i j, k l}=\frac{\exp \left(\kappa_{r g b}^{i j, k l}\right)}{\sum_{(x, y)} \exp \left(\kappa_{r g b}^{i j, x y}\right)}+w_{3} \frac{\exp \left(\kappa_{\text {pos }}^{i j, k l}\right)}{\sum_{(x, y)} \exp \left(\kappa_{\text {pos }}^{i j, x y}\right)}, κij,kl=∑(x,y)exp(κrgbij,xy)exp(κrgbij,kl)+w3∑(x,y)exp(κpos ij,xy)exp(κpos ij,kl),
公式10:
M t i , j , c = ∑ ( k , l ) ∈ N ( i , j ) κ i j , k l M t − 1 k , l , c M_{t}^{i, j, c}=\sum_{(k, l) \in \mathcal{N}(i, j)} \kappa^{i j, k l} M_{t-1}^{k, l, c} Mti,j,c=(k,l)∈N(i,j)∑κij,klMt−1k,l,c
需要注意的是,refinement是迭代优化的,我们可以理解为,利用当前位置(像素/特征)和邻域内其他位置处间的联系,来更新当前l位置的label。其迭代次数 t t t,所用到的膨胀卷积的膨胀系数,以及 w 1 , W 2 , W 3 w_1, W_2, W_3 w1,W2,W3 等超参数设置将在后面实验部分给出。
损失函数
整个模型包含四项损失:
-
“类别预测”对应的多标签分类损失
Multi-label Soft Margin Loss -
“分割预测”对应的交叉熵损失
Cross-entropy Loss -
本文定义的亲和度损失
Affinity Loss -
其他文章[4] 用过的正则损失
Regularized Loss Loss
完整的损失函数如下:
L = L c l s + λ 1 L seg + λ 2 L a f f + λ 3 L reg \mathcal{L}=\mathcal{L}_{c l s}+\lambda_{1} \mathcal{L}_{\text {seg }}+\lambda_{2} \mathcal{L}_{a f f}+\lambda_{3} \mathcal{L}_{\text {reg }} L=Lcls+λ1Lseg +λ2Laff+λ3Lreg
其中 λ \lambda λ 用户调节各项损失的权重。
类别损失 L cls \mathcal{L}_{\text {cls }} Lcls
这里的类别损失 L cls \mathcal{L}_{\text {cls }} Lcls 实际上就是一个多标签损失,其定义如下:
L c l s = 1 C ∑ c = 1 C ( y c log ( p c l s c ) + ( 1 − y c ) log ( 1 − p c l s c ) ) \mathcal{L}_{c l s}=\frac{1}{C} \sum_{c=1}^{C}\left(y^{c} \log \left(p_{c l s}^{c}\right)+\left(1-y^{c}\right) \log \left(1-p_{c l s}^{c}\right)\right) Lcls=C1c=1∑C(yclog(pclsc)+(1−yc)log(1−pclsc))
亲和度矩阵损失 L aff \mathcal{L}_{\text {aff }} Laff
这里我们着重强调下 L aff \mathcal{L}_{\text {aff }} Laff ,文中所给出的公式如下:
L a f f = 1 N − ∑ ( i j , k l ) ∈ R − ( 1 − sigmoid ( A i j , k l ) ) + 1 N + ∑ ( i j , k l ) ∈ R + sigmoid ( A i j , k l ) \begin{aligned} \mathcal{L}_{a f f} &=\frac{1}{N^{-}} \sum_{(i j, k l) \in \mathcal{R}^{-}}\left(1-\operatorname{sigmoid}\left(A^{i j, k l}\right)\right) \\ &+\frac{1}{N^{+}} \sum_{(i j, k l) \in \mathcal{R}^{+}} \operatorname{sigmoid}\left(A^{i j, k l}\right) \end{aligned} Laff=N−1(ij,kl)∈R−∑(1−sigmoid(Aij,kl))+N+1(ij,kl)∈R+∑sigmoid(Aij,kl)
实验
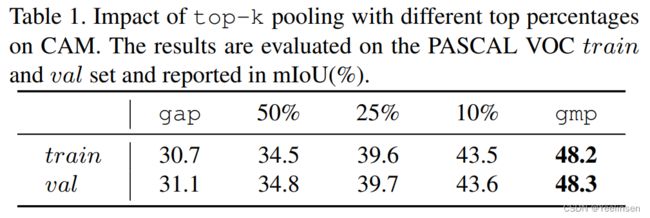
pooling方法
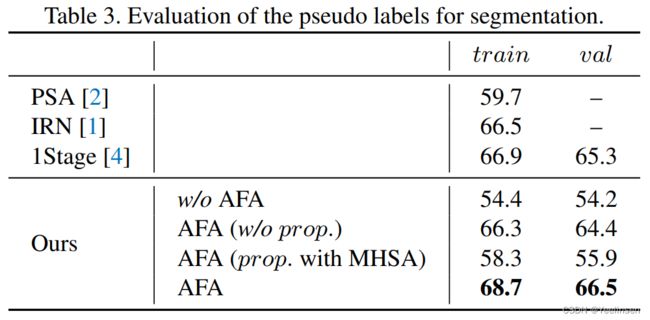
本文所提各个模块的有效性
与其他方法的比较
一些超参数的设置
参考
[1] Learning Affinity from Attention: End-to-End Weakly-Supervised Semantic Segmentation with Transformers, CVPR 2022
[2] 简记:Learning Affinity from Attention: End-to-End Weakly-Supervised Semantic Segmentation with Transformers – hxhen的点滴记录
[3] Learning Pixel-level Semantic Affinity with Image-level Supervision for Weakly Supervised Semantic Segmentation, Jiwoon Ahn and Suha Kwak, CVPR 2018
[4] On Regularized Losses for Weakly-supervised CNN Segmentation, Meng Tang, Federico Perazz, ECCV 2018
[4] On Regularized Losses for Weakly-supervised CNN Segmentation, Meng Tang, Federico Perazz, ECCV 2018