哈工大机器学习实验一多项式拟合正弦函数
一、实验目的
- 掌握最小二乘法求解(无惩罚项的损失函数)
- 掌握加惩罚项(2范数)的损失函数优化
- 掌握梯度下降法、共轭梯度法
- 理解过拟合、克服过拟合的方法(如加惩罚项、增加样本)
二、实验要求及环境
实验要求:
-
生成数据,加入噪声;
-
用高阶多项式函数拟合曲线;
-
用解析解求解两种loss的最优解(无正则项和有正则项)
-
优化方法求解最优解(梯度下降,共轭梯度);
-
用你得到的实验数据,解释过拟合。
-
用不同数据量,不同超参数,不同的多项式阶数,比较实验效果。
-
语言不限,可以用matlab,python。求解解析解时可以利用现成的矩阵求逆。梯度下降,共轭梯度要求自己求梯度,迭代优化自己写。不许用现成的平台,例如pytorch,tensorflow的自动微分工具。
实验环境:
- pycharm 2019.1
- python 3.7
- win10
- X86-64
三、设计思想
1.算法原理
最小二乘法: 又称最小平方法,是一种数学优化方法。它通过最小化误差的平方和寻找数据的最佳函数匹配。因此我们定义损失函数:
L ( ω ) = 1 2 N ∑ ω ( y − X ω ) 2 L(\omega) = \frac{1}{2N}\sum_{\omega}(y-X\omega)^2 L(ω)=2N1ω∑(y−Xω)2
其中 X = ( x 11 x 12 ⋯ x 1 d 1 x 21 x 22 ⋯ x 2 d 1 ⋮ ⋮ ⋱ ⋮ ⋮ x m 1 x m 2 ⋯ x m d 1 ) = ( x 1 T 1 x 2 T 1 ⋮ ⋮ x m T 1 ) X =\left(\begin{array}{cc} x_{11} &x_{12} & \cdots &x_{1d} & 1 \\x_{21} &x_{22} &\cdots &x_{2d} & 1\\ \vdots &\vdots & \ddots &\vdots & \vdots \\ x_{m1} &x_{m2} &\cdots &x_{md} & 1 \end{array}\right) = \left(\begin{array}{cc} x_{1}^T &1\\x_2^T &1\\ \vdots &\vdots \\ x_m^T &1 \end{array}\right) X=⎝⎜⎜⎜⎛x11x21⋮xm1x12x22⋮xm2⋯⋯⋱⋯x1dx2d⋮xmd11⋮1⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛x1Tx2T⋮xmT11⋮1⎠⎟⎟⎟⎞
于是求解 ω \omega ω使得 ω ^ ∗ = a r g m i n ω ^ ( y − X ω ^ ) T ( y − X ω ^ ) \hat{\omega}^* = \mathop {argmin}\limits_{\hat{\omega}} (y-X\hat{\omega})^T(y-X\hat{\omega}) ω^∗=ω^argmin(y−Xω^)T(y−Xω^)
令 E ω ^ = ( y − X ω ^ ) T ( y − X ω ^ ) E_{\hat{\omega}} = (y-X\hat{\omega})^T(y-X\hat{\omega}) Eω^=(y−Xω^)T(y−Xω^), 对 ω ^ \hat{\omega} ω^求导得到 ∂ E ω ^ ∂ ω ^ = 1 N X T ( X ω ^ − y ) \frac{\partial E_{\hat{\omega}}}{\partial \hat{\omega}} = \frac{1}{N}X^T (X\hat{\omega}-y) ∂ω^∂Eω^=N1XT(Xω^−y)
令上式(在梯度下降法中,上面这个式子也是梯度)等于0可得
( X T X ) ω ^ ∗ = X T y (X^TX)\hat{\omega}^*=X^Ty (XTX)ω^∗=XTy
如果 X T X X^TX XTX可逆,则可以直接求解 ω = ( X T X ) − 1 X T y \omega =(X^TX)^{-1}X^Ty ω=(XTX)−1XTy得到解析解;
或者直接运用共轭梯度法求解上面这个方程。
另外,我们在求解析解时,可以在损失函数后面加上 ∣ ∣ ω ∣ ∣ 2 ||\omega||_2 ∣∣ω∣∣2作为惩罚项,比例因子记为 λ \lambda λ, 防止模型太复杂而产生过拟合。加入惩罚项的损失函数为
L ( ω ) = 1 2 N ∑ ω ( y − X ω ) 2 + λ 2 ∣ ∣ ω ∣ ∣ 2 L(\omega) = \frac{1}{2N}\sum_{\omega}(y-X\omega)^2+ \frac{\lambda}{2}||\omega||_2 L(ω)=2N1ω∑(y−Xω)2+2λ∣∣ω∣∣2
利用解析解的方式可以求得
ω = ( X T X + λ N I ) − 1 X T y \omega = (X^TX+\lambda NI)^{-1}X^Ty ω=(XTX+λNI)−1XTy
因为 X T X + λ N I X^TX+\lambda NI XTX+λNI一定可逆,我们可以用这种方式求带惩罚项的解析解
2.算法的实现
- 生成噪声:调用random库,生成高斯噪声

- 求解析解直接套用算法原理中的公式即可
- 梯度下降法:当梯度的2范数小于我们设置的阈值e时,结束迭代(其中lamda是梯度下降法的学习率)

4.共轭梯度下降法:关键代码如下

四、实验结果与分析
分析一:以20数据量为例,分析不同方法对于不同阶的拟合程度
4.1解析式法(不带正则项)
4.1.1研究数据量为20时不同阶数的拟合
一阶

二阶

三阶

四阶

五阶

六阶

七阶

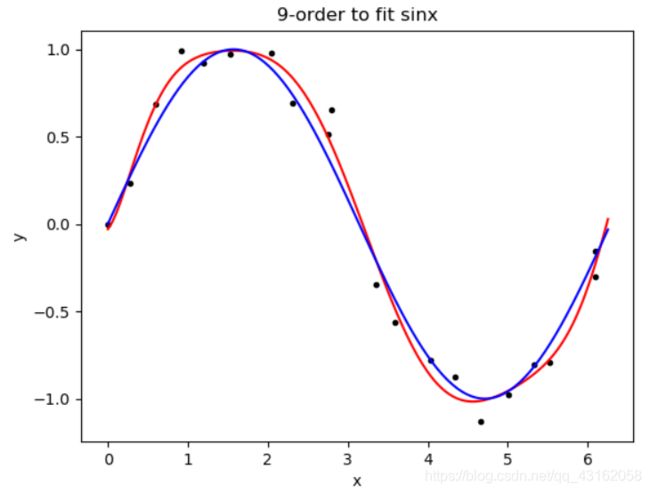
八阶(明显过拟合了)

九阶(过拟合)

4.1.2针对会出现过拟合的八阶拟合,再选用不同的数据量进行比较
不同数据量的平均loss(由于数据量较小时会出现过拟合,所以损失会比较小;当数据规模持续增大,过拟合会减弱,因此损失会增大;当数据量超过90时,曲线已经几乎不出现过拟合的现象,且loss相比6,7阶下降了许多。增大数据量也是克服过拟合的一种手段)

数据量为10

数据量为20

数据量为30

数据量为40

数据量为50

数据量为60

数据量为70
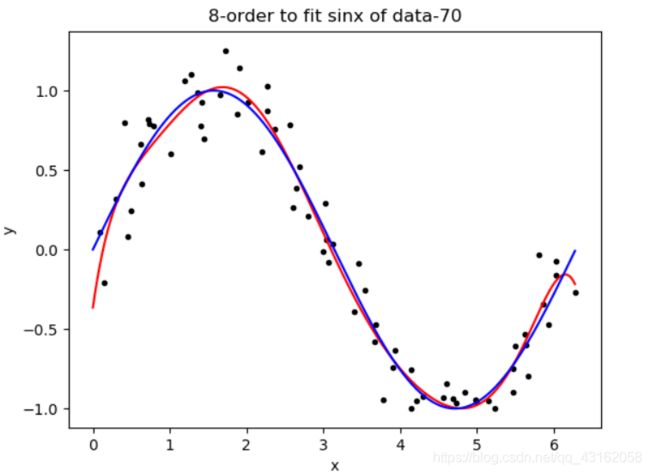
数据量为80

数据量为90

4.2 解析式法(带正则项)
4.2.1当数据量为20时,研究不同的阶数的拟合效果
不同阶的损失如下图,其中 λ = 0.0001 \lambda = 0.0001 λ=0.0001

一阶

二阶

三阶

四阶

五阶

六阶

七阶

八阶

九阶

可以看出,相比不带正则项的解析式解法,8,9阶的过拟合有所好转,(下图单独对这两个进行比较)仍然出现过拟合可能是前面的参数不够好的缘故,接下来会讨论不同的 λ \lambda λ取值的影响
![]()
4.2.1数据量为20时,不同 λ \lambda λ取值对曲线过拟合的影响
取从0至0.01的,绘制出了如下曲线,可以看出当 λ \lambda λ较小时,loss比较小(不含正则项的loss,因为正则项的loss太大了),即使取到0.01,loss值仍然在可接受范围

我们再取一个更小的区间

再缩小

继续缩小
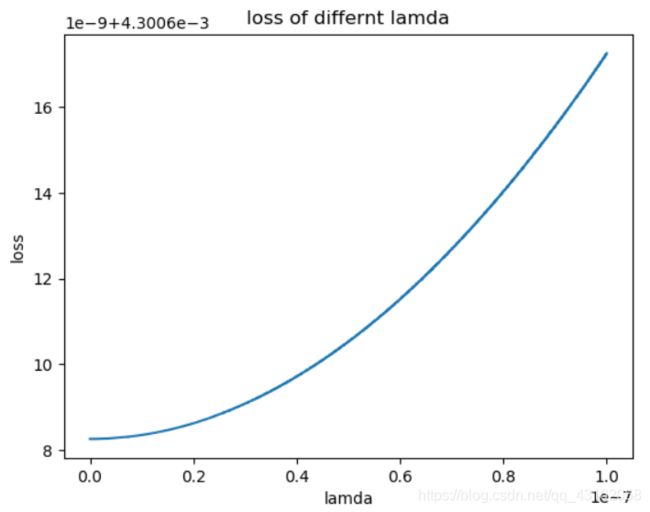
根据上面的loss图,我们抽取 λ = 1 e − 1 , 1 e − 2 , 1 e − 3 , 1 e − 4 , 1 e − 5 , 1 e − 6 \lambda=1e-1,1e-2,1e-3,1e-4,1e-5,1e-6 λ=1e−1,1e−2,1e−3,1e−4,1e−5,1e−6分布和不带正则项的解析式法去比较。
当 λ = 1 e − 1 \lambda=1e-1 λ=1e−1时

当 λ = 1 e − 2 \lambda=1e-2 λ=1e−2时
 当 λ = 1 e − 3 \lambda=1e-3 λ=1e−3时
当 λ = 1 e − 3 \lambda=1e-3 λ=1e−3时
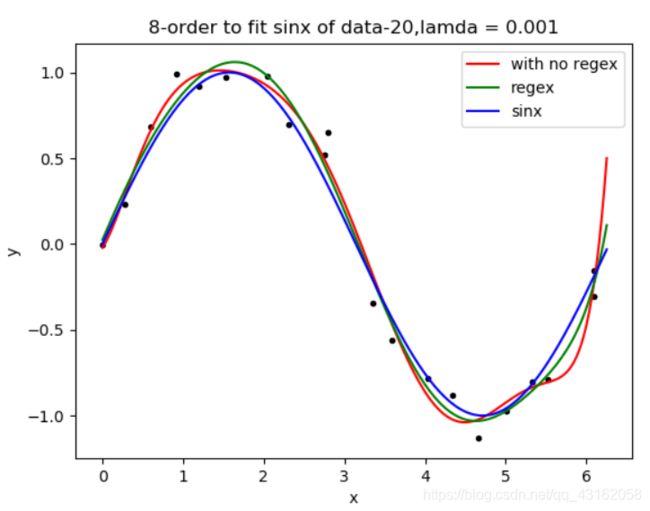
当 λ = 1 e − 4 \lambda=1e-4 λ=1e−4时

当 λ = 1 e − 5 \lambda=1e-5 λ=1e−5时,带正则和不带正则的曲线几乎重合,此时正则系数过小

当 λ = 1 e − 6 \lambda=1e-6 λ=1e−6时,不带正则的曲线和带正则的曲线完全重合

由以上信息可以得出, λ \lambda λ在从0.1到1e-6变化的过程中,曲线有一个拟合先变好再过拟合的过程,我们对lamda取0.01至0.001之间的数进行分析,寻找比较好的值.
先取0.005

再取一下0.002,可以看出和0.001,0.005以及0.01区别不大,可以猜测应该是受数据量的影响,所以拟合得不好。接下来我们减少数据量为10

λ = 0.01 \lambda=0.01 λ=0.01

λ = 0.05 \lambda=0.05 λ=0.05可以看出效果仍然不太好,调小一点

λ = 0.03 \lambda=0.03 λ=0.03如下图,比0.05要好一些,但依然不太理想

再取0.02,不如0.01效果好

又继续减小,当 λ \lambda λ在0.0001至0.01这个区间的拟合都是比较好的,已经不会发生过拟合了



从上面的分析过程还可以得出,不同阶数不同数据量的 λ \lambda λ取值各不相同,当阶数为8,数据量在50以上时,基本不需要正则化也可以拟合得很好
4.2.3关于不同阶数的拟合效果(研究时我们将lamda调到最佳,以数据量为10作为研究)
由前面的可以看出一二阶拟合效果并不好,因此不作进一步观察
三阶

四阶

五阶
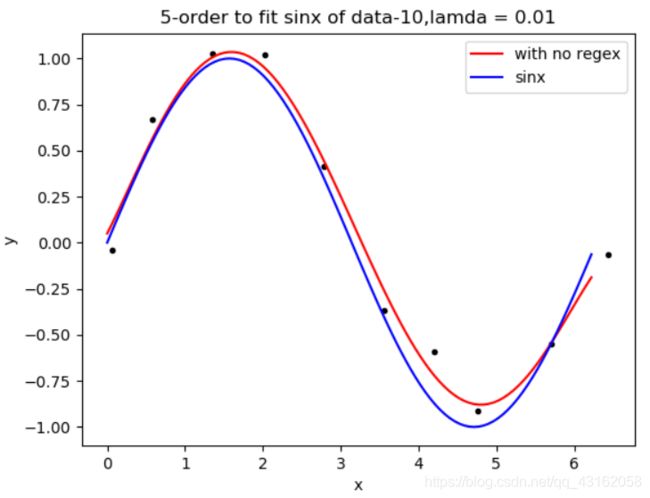
六阶

七阶
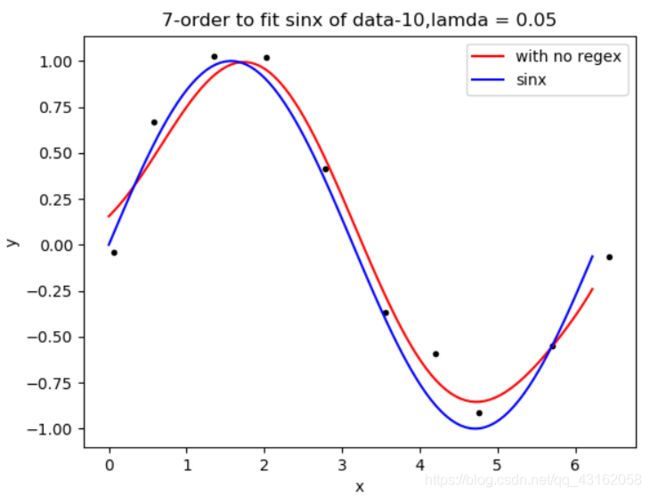
八阶

九阶

由上可以看出,三阶已经拟合得可以接受了,但是还不够,从5阶到8阶都可以拟合得很接近正弦曲线了,但是九阶的拟合依然有点过拟合(也可能是对于参数的寻找要求更高一些)。
4.3梯度下降法
4.3.1不同阶数的梯度下降法
4.3.2 关于步长的选取(以5阶,数据量为10为例)
步长为1e-6

步长为2e-6

步长为5e-7时,运行时间比较长,拟合效果也不太好

从这几组数据来看,1e-6拟合得最好,当增大步长时,矩阵运算过程中会发生溢出,当继续减小步长时,由于步长太小对精度非常敏感,但是如果继续下调精度收敛速度会很慢。
4.4共轭梯度法
数据量为20时不同阶数共轭梯度法的损失如下图所示,从三阶开始损失以及比较小了
一阶

二阶

三阶

四阶

五阶

六阶

七阶

八阶(开始出现明显的过拟合)

九阶

由此可以得出结论,当阶数为1,2时,损失特别大,可能原因是矩阵运算过程中产生了一些误差,并且阶数太小精度不够;3-9阶的损失都比较小,但是阶数为8,9时出现了明显的过拟合。随后我开始增大数据规模,当数据量增大到为40,7阶也出现了过拟合现象

当数据量大于50时,7-9阶基本没有出现出现过拟合现象。
综上,当数据量为10-100时,使用5,6阶拟合sinx损失小,且不会出现过拟合
五、结论
- 通常情况下解析解能解决大多数拟合问题,但是( X T X X^TX XTX)不一定可逆。
- 当数据量和阶数相当时,直接使用最小二乘法容易过拟合,可以通过加入正则项解决。关于正则因子的选择,它与数据量和阶数都相关。通常情况下,数据量越大,正则因子越大;阶数越大,正则因子越大。正则+解析式方法是最简便同时又不容易过拟合的方法,但是正则因子的选择很困难。
- 为了避免谈论( X T X X^TX XTX)是否可导的问题,我们可以采取梯度下降法或者共轭梯度法来替代。梯度下降法很直接,但是下降速度比较慢,而且关于步长的选择及其严苛。共轭梯度法下降速度快,且能得到几乎和解析式重合的拟合曲线,在应对高维数据时具有明显优势。但是共轭梯度法理解起来不够直观,想要改进也比较困难。
- 本实验讨论的损失函数时凸函数,对于非凸函数问题不适用(主要体现在梯度下降法需要给出跳出局部最优的条件。
- 多项式拟合函数能力很强,但是阶数不宜太高,否则在运算过程中容易溢出(当样例中的x比较大,对x乘方很容易溢出)
六、参考文献
机器学习【周志华】
统计学习方法【李航】
数值分析【李庆扬,王能超,易大义】
七、附录:源代码(带注释)
import numpy as np
from numpy import *
import matplotlib.pyplot as plt
np.seterr(divide="ignore", invalid='ignore')
#求解矩阵X
def calX(dataAmount, n, dataMatrix):
X = ones((dataAmount, n+1)) #初始化
for i in range(dataAmount):
for j in range(n):
X[i][j] = dataMatrix[i][0]**(j+1)
X[i][n] = 1
return X
def cal(x, n, w):
rel = 0
for j in range(n):
rel += x**(j+1)*w[j]
rel += w[n]
return rel
#计算loss(不带惩罚项)
def calLoss(w, y, X, dataAmount):
rel = y - np.dot(X, w)
return np.dot(rel.T, rel)/(2*dataAmount)
#不带正则项的解析解
def analysis(dataAmount, n):
doc = str(dataAmount) + ".txt"
dataMatrix = np.loadtxt(doc, dtype=float)
cols = dataMatrix.shape[-1]
y = dataMatrix[:, cols-1:cols]
X = calX(dataAmount, n, dataMatrix)
w = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X)), X.T), y)
loss = calLoss(w, y, X, dataAmount)
dx = []
dx1 = []
d = 2 * np.pi / (dataAmount * 10)
cnt = 0
for i in range(dataAmount):
dx1.append(dataMatrix[i][0])
for i in range(dataAmount * 10):
dx.append(cnt)
cnt += d
dy = []
dy1 = []
for i in range(dataAmount):
dy1.append(dataMatrix[i][1])
for i in range(len(dx)):
dy.append(cal(dx[i], n, w))
plt.plot(dx, dy, 'r')
plt.plot(dx, sin(dx), 'b')
plt.scatter(dx1, dy1, c="#000000", marker='.')
plt.xlabel("x")
plt.ylabel("y")
plt.title(str(n) + "-order to fit sinx of data-"+str(dataAmount))
plt.show()
return loss[0][0]
#analysis(40,7)
#带正则项的解析解
def analysis_regex(dataAmount, n,lamda):
doc = str(dataAmount) + ".txt"
dataMatrix = np.loadtxt(doc, dtype=float)
cols = dataMatrix.shape[-1]
y = dataMatrix[:, cols-1:cols]
X = calX(dataAmount, n, dataMatrix)
I = eye(n+1)
w = np.dot(np.dot(np.linalg.inv(np.dot(X.T, X) + lamda*dataAmount*I), X.T), y)
loss1 = calLoss(w,y,X,dataAmount) #对比不同lamda的损失
#loss = calLoss(w, y, X, dataAmount) + lamda*np.dot(w.T, w)/2
"""
dx = []
dx1 = []
d = 2 * np.pi / (dataAmount * 10)
cnt = 0
for i in range(dataAmount):
dx1.append(dataMatrix[i][0])
for i in range(dataAmount * 10):
dx.append(cnt)
cnt += d
dy = []
dy1 = []
for i in range(dataAmount):
dy1.append(dataMatrix[i][1])
for i in range(len(dx)):
dy.append(cal(dx[i], n, w))
plt.plot(dx, dy, 'r')
plt.plot(dx, sin(dx), 'b')
plt.scatter(dx1, dy1, c="#000000", marker='.')
plt.xlabel("x")
plt.ylabel("y")
plt.title(str(n) + "-order to fit sinx of data-"+str(dataAmount))
plt.show()
"""
return loss1[0][0]
#analysis_regex(20,8,0.001)
#求梯度
def gradient(X,w,y, dataAmount):
return np.dot(X.T, np.dot(X, w)-y)/dataAmount
#梯度下降法
def de_gradient(dataAmount,n,lamda):
doc = str(dataAmount) + ".txt"
dataMatrix = np.loadtxt(doc, dtype=float)
cols = dataMatrix.shape[-1]
y = dataMatrix[:, cols-1:cols]
X = calX(dataAmount, n, dataMatrix)
w = 0.1*ones((n+1, 1))
on = 0.000001
g0 = gradient(X, w, y, dataAmount)
#cnt = 5000000
while 1:
#loss = calLoss(w, y, X, dataAmount)
w += (-lamda) * g0*1000
print(g0)
#loss1 = calLoss(w, y, X, dataAmount)
g = gradient(X, w, y, dataAmount)
#cnt -= 1
if np.linalg.norm(g-g0) < on:
break
g0 = g
dx = []
dx1 = []
d = 2 * np.pi / (dataAmount * 10)
cnt = 0
for i in range(dataAmount):
dx1.append(dataMatrix[i][0])
for i in range(dataAmount * 10):
dx.append(cnt)
cnt += d
dy = []
dy1 = []
for i in range(dataAmount):
dy1.append(dataMatrix[i][1])
for i in range(len(dx)):
dy.append(cal(dx[i], n, w))
plt.plot(dx, dy, 'r')
plt.plot(dx, sin(dx), 'b')
plt.scatter(dx1, dy1, c="#000000", marker='.')
plt.xlabel("x")
plt.ylabel("y")
plt.title(str(n) + "-order to fit sinx of data-"+str(dataAmount))
plt.show()
loss = calLoss(w, y, X, dataAmount)
return loss[0][0]
de_gradient(10,4,0.0000000001)
#共轭梯度法
def cj_gradient(dataAmount,n):
doc = str(dataAmount) + ".txt"
dataMatrix = np.loadtxt(doc, dtype=float)
cols = dataMatrix.shape[-1]
y = dataMatrix[:, cols - 1:cols]
X = calX(dataAmount, n, dataMatrix)
A = np.dot(X.T, X)
w = zeros((n+1, 1))
b = np.dot(X.T, y)
r = b - np.dot(A, w)
p = r
while 1:
if np.dot(r.T, r) == 0 or np.dot(np.dot(p.T, A),p) == 0:
break
a = np.dot(r.T, r) / np.dot(np.dot(p.T, A),p)
w += a*p
r1 = r - np.dot(a*A, p)
beta = np.dot(r1.T, r1)/np.dot(r.T, r)
p = r1 + beta*p
r = r1
loss = calLoss(w, y, X, dataAmount)
dx = []
dx1 = []
d = 2*np.pi/(dataAmount*10)
cnt = 0
for i in range(dataAmount):
dx1.append(dataMatrix[i][0])
for i in range(dataAmount*10):
dx.append(cnt)
cnt += d
dy = []
dy1 = []
for i in range(dataAmount):
dy1.append(dataMatrix[i][1])
for i in range(len(dx)):
dy.append(cal(dx[i], n, w))
plt.plot(dx, dy, 'r')
plt.plot(dx, sin(dx), 'b')
plt.scatter(dx1, dy1, c="#000000", marker='.')
plt.xlabel("x")
plt.ylabel("y")
plt.title(str(n)+"-order to fit sinx of data-"+str(dataAmount))
plt.show()
return loss[0][0]
#cj_gradient(40,7)
#比较数据量为20时不同阶不带正则项解析解的损失
def main1(max_n):
dataAmount = 20
x = []
for i in range(1,max_n):
x.append(i)
y = []
for i in range(1,max_n):
y.append(analysis(dataAmount, x[i-1]))
plt.plot(x, y, 'b')
plt.title("different order's loss")
plt.xlabel("order")
plt.ylabel("loss")
plt.show()