线性代数和矩阵论 基础概念再理解

本文送给修过线性代数和矩阵论，但是考完试后全忘了的朋友。个人理解仅供参考，如果有误欢迎指正。

行列式

第二种定义：

从第二种定义可以想到，任意行列都可以展开，故行列式转置后结果不变。行和列具有对等地位。

计算行列式时注意代数余子式和余子式的区别。

从第二种定义理解交换两行后变号：交换两行可以看成2(j-i)-1次相邻交换，因此逆序数的变化一定是奇数。

用途之一是，给出多元一次方程组的通解。个人认为行列式使得计算机能容易解决多元一次方程组。

有人说矩阵是对非单位阵、经典坐标系（个人说法不严谨，就是指自然基那一套）空间的扭曲形变。行列式的英文是determinant，缩写为det，就是扭曲后的单位向量围成的空间的体积，可以衡量形变的程度。https://zhuanlan.zhihu.com/p/146551798。下图的矩阵的第一列感觉应该是(2,1)，直观展示了“形变”的理解。

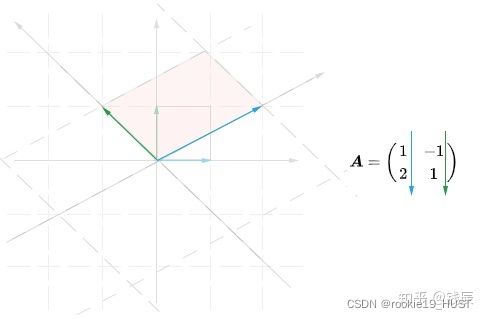
cramer法则，系数行列式不为0则有唯一解。n个未知数需要n个独立方程。

注意，行列式是方程数等于未知数数时的特例，也就是说行列式肯定是方的。从递归定义肯定也能推断出这一点。

一个结论是，行列式等于特征值的连积。

矩阵是什么

方程组系数视角：一开始是为了解决一般的多元一次方程组（方程数可以小于未知数的数）。
映射视角：m x n矩阵是线性变换，是函数。其输入是n维列向量，输出是m维列向量。
基视角：考虑Ax=b，A为矩阵，x和b是列向量，这个可以写成Ax=Ib，也就是说，同一个向量在不同的基下仍然是同一个东西，x是向量在基A下的坐标，b是向量在自然基下的坐标。

因此矩阵乘法就是映射的复合。矩阵乘法的结合律就是映射的结合律。

至于为什么写成gf，原因是f是先作用的，g是后作用的。gf(a)的意思就是g(f(a))，表示把f作用结果作为g的输入。
显然，映射不满足交换律，因为定义域和值域未必能对应上。

矩阵乘法的计算习惯

除了最开始学的点积写法，其实也有其它的理解，
行视角，将第一个矩阵看成行向量。

列视角，将第二个矩阵看成列向量。



矩阵右乘一个列向量，相当于对矩阵的列进行线性组合；
矩阵左乘一个行向量，相当于对矩阵的行进行线性组合。

当我们说，矩阵A的列向量的线性组合，其实就是在说Ax，x是一个列向量。

酉矩阵，酉变换

酉变换是线性变换。
酉矩阵的行列式为±1。
一个没用的解释是，酉变换就是乘一个酉矩阵，酉矩阵就是满足AA^H=A^HA=I的矩阵。
更本质的解释是，酉变换不改变向量的长度，不改变复空间中向量的内积（据此可推出酉矩阵特征值的模长为1）。想想量子逻辑门，酉变换不影响概率归一性，可以辅助记忆。
不改变长度，可以视为旋转变换。可以通过公式求出旋转轴和旋转角。以过原点平面为镜面的变换，其矩阵为I-2uu^T（与投影变换的很像，走一步是投影，走两步就是镜像了）

各个变换中的不变

初等行变换就是方程组消元，不会改变独立方程的个数，因此不会改变秩。
相似变换就是同一个线性变换的易容术，不会改变特征值。

一些结论

如果矩阵不可逆，说明对应行列式为0，特征值的积为0，那至少有一个零特征值。
如果矩阵特征值全为0，则其幂零。反之亦然。
矩阵幂零，则其Jordan标准型幂零，每一个Jordan块也幂零，则其特征值全为0。
A和AA^T的零空间相等，故像空间的维数相等，结合R(AA^T)包含于R(A)，可知R(AA^T)=R(A)。

投影变换

向量到平面的投影Pα = α-(u,α)u，可以从此式看出，P对应的矩阵为I-uu^T。

如何理解矩阵乘积的行列式等于行列式的乘积

为什么 |AB|=|A||B| ，这意味着什么。这个问题我还是没想明白，先当结论记吧。

为什么要定义对称矩阵

有人认为原因是对称矩阵有很好的性质。
实对称矩阵一定可以对角化。
实对称矩阵一定有标准正交的特征向量。

可逆意味着什么

可逆=满秩=非奇异

可逆和方程解数的关系

可逆，意味着它是单射，所以Ax=b有唯一解。

为什么可逆和行列式有关

行列式不为0是可逆的充要条件 。
可逆， |AA^-1|=|A||A^-1|=|i|=1,因此行列式不为0
行列式不为0，就能用伴随矩阵数乘1/|A|来构造出逆矩阵。
我个人感觉，可逆这个概念是从映射和变换角度来看待矩阵的，而行列式和有解/满秩是从方程组的角度来看待矩阵的。所以没有特别直观的解释。

矩阵求逆

矩阵求逆可以看成解了一个线性方程组，可以用来衡量计算量。

特征值，特征向量，特征分解

几何意义，将矩阵视为变换，则特征向量只会被矩阵拉伸，而不会被旋转。
特征值到底体现了矩阵的什么特征？为啥叫特征值？
秩等于特征向量个数，把所有的特征向量排出来，



V里的就是特征向量，Λ里的的就是特征值。
这也就意味着，找出所有的特征值和特征向量，就能还原出原来的矩阵。所以称之为“特征”也算合理。特征分解也叫谱分解，n阶方阵A的n个特征值称为A的谱。
此外，还有主特征值之说。https://zhuanlan.zhihu.com/p/314464267
矩阵反复作用于任意向量，结果会逐渐接近最大特征值对应的特征向量。
最大特征值就是主特征值。图像处理时，用图像最大的几个特征值就能大致复原原图。
也就是说，主特征值代表了矩阵的某种内在特征，代表了矩阵作为变换的主要方向。
对角化的充要条件之一是n个线性无关的特征向量（可以不必有n个不同的特征值，证明用基），此外矩阵论还讲了好几个。如果不能对角化，那就退求其次Jordan化。
能对角化的时候，我们发现矩阵按列分块后形成的列向量恰好满足特征向量的定义。所以对角化和特征向量联系紧密。

特征值的和等于矩阵的迹，特征值的积等于矩阵的行列式。

特征值和可逆的关系

将矩阵看成映射。
特征值中如果有0，说明有一部分非零向量会被映射到0，故这个矩阵肯定不可逆。

对角矩阵

考虑到特征分解，对角矩阵可以分解为单位矩阵和它自己，所以对角矩阵的对角线就是其特征值。

代数重数和几何重数

图源自知乎@123。
代数重数和几何重数是对于单个特征值而言的。

Jordan矩阵，Jordan化

仔细观察Jordan矩阵，发现包含特征值、代数重数、几何重数三个信息。
每个特征值对应一个Jordan矩阵，其线性无关特征向量的个数即为Jordan矩阵中Jordan块的个数，也就是几何重数。
对每个线性无关的特征向量，解Jordan链，确认Jordan链的长度，就能得到Jordan矩阵中的每个Jordan块的尺寸（知道尺寸也就知道了Jordan块）。于是就得到了Jordan标准型。
至于P，Jordan链就是P矩阵。为什么呢，注意到我们对P做了两次按列分块，第一次是有几个特征值就分成几块，第二次是在第一次分出来的块上再分，特征值有几个线性无关特征向量就分几块。每解一条Jordan链，就能得到第二次的一块。

矩阵分解

https://zhuanlan.zhihu.com/p/183065884
矩阵分解的用途非常广泛，比较常用的有奇异值分解 (Singular Value Decomposition 以下简称 SVD分解)，Schur分解，特征值分解(对于可对角化矩阵而言)，Jordan分解(对于不可对角化矩阵而言)等等。矩阵分解的目的很明确，一方面是为了“打开”矩阵，使得矩阵的信息更加一目了然，比如将一个矩阵进行SVD分解后我们就能知道了矩阵的秩，范数(2-范数，F-范数等等)和矩阵条件数等等；另一方面是为了方便对矩阵进行计算，比如解线性方程组，线性最小二乘问题等等。
三角分解（如LU和LDV分解）和满秩分解都可以通过行变换求得。
极分解将一个变换分成旋转变换和拉伸变换两个部分，先求出奇异值分解之后易得极分解。

为什么要提出SVD

一个矩阵，若为n阶方阵，并且有n个线性无关的特征向量，那么它可以对角化，或者说特征分解。
任何矩阵都可以相似于Jordan矩阵。但可惜Jordan次对角线0、1不确定。
正规矩阵 等价于 矩阵可酉相似对角化。
SVD可以看成是，任意尺寸矩阵，的一种广义特征分解。通过构造A^HA这个正规矩阵来做到，逻辑大概如下：
任何矩阵A都有共轭转置A^H。所以每个矩阵A都对应一个A^HA。
因此，任何矩阵A都对应一个能够酉相似对角化的矩阵。
于是任何矩阵A都对应一个对角矩阵。

满秩分解

满秩分解有助于计算广义加号逆，也称MP逆。
A=BC，A是m x n矩阵，秩为r。B是m x r矩阵，秩为r。C是r x n矩阵，秩为r。
则其MP逆可以由公式求得：C^H(CC^H)^-1(B^HB)^-1B。
满秩分解只用初等行变换就能完成，手法比较简单。

向量空间，线性空间，零空间，列空间

向量空间，如R3。空间由集合和运算定义，有点像代数系统。集合中的元素，加法和乘法后仍在空间中。R3的子空间如任意一个过零点的平面。向量空间中肯定有零向量。
矩阵可以看成一系列向量，也就是向量集合。再加上矩阵加法和矩阵数乘就成为空间了。
穷尽列向量的线性组合后形成的空间，就是列空间。
零空间虽然经常跟列空间一起谈，但其实其组成内容完全不一样。列空间是矩阵A中的列张成的，而零空间是使Ax=0的x组成的。一个源于A，一个源于x。
列空间是使Ax=b的有解的那些b，零空间是Ax=0的解空间。
列空间和像空间是同一个东西的两种看待方式。

线性算子乘积只缩小秩

由线性性易证，零向量总是映射到零向量。
零总是映射到零。非零可能映射到零，也可能映射到非零。所以对一个空间使用线性算子，秩（像空间维数）只会缩小。

秩，行秩，列秩

从方程组系数角度来看，秩是独立方程的个数。
行秩是行向量线性无关组的大小，列秩是列向量线性无关组的大小。秩是列空间的维数。
直觉上，维度丢失，是因为被映射到0了。所以线性代数基本定理是，列空间维数 r ，零空间维数n-r。

关于行秩=列秩=秩，我看见、想到两种解释，感觉都能说得通。
第一种，设A为m x n的矩阵，A=BD，B为m x c，D为c x n，c为列秩。由于乘积只可能缩小乘数的秩，所以r≤m，r≤c。
同理，A=PQ，P为m x r，Q为r x n，r为行秩，则c≤r，c≤n。可见r=c。
第二种，设A=BD，将D看成列向量（即把A和D的每一行包装为一个整体）。B是m x c行，D是c x 1行，A是m x 1行。
则A的每一行是D每一行的线性组合。因此A的行空间维数不会超过D的行数，故r≤c。
对A的转置进行类似的推导，可以得到c≤r。所以r=c。

正交补子空间

设U是内积空间的子空间，设U(右上角⊥)是其正交补子空间。
这个术语应该分成三部分，正交，补，子空间。
定义式中只要求正交，即U(右上角⊥)中的每一个向量，都跟U中所有向量内积为0。
可以证明这个定义下，U(右上角⊥)是一个子空间，而且与U互补（与U直和之后即为内积空间）。

线性变换

变换是指集合到自己的映射。
原来共线的三点，线性变换后仍然共线。
线性变换是自同态。未必同构，故未必可逆。
随着基的改变，同一个线性变换就有不同的矩阵，这些矩阵是相似的。
用Jordan化方法找到线性变换对应的最简单的矩阵。

相似矩阵

相似的意义是，他们是同一个线性变换在不同基下的面貌。他们的特征值相同，特征向量不同。
设A是线性变换T在基(α1, α2, … αn)下的矩阵，A的特征向量为X。则X是线性变换的特征向量ξ在基下的坐标。

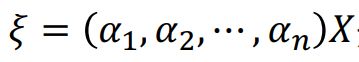
相似矩阵可以化为一样的Jordan标准型，因此相似矩阵的最小多项式相同。这也侧面反映了Jordan标准型的好处，可以一眼看出其最小多项式。有了Jordan标准型，可以利用最小多项式降次，可以利用形似泰勒展开的上三角矩阵计算每一个Jordan块经过多项式运算后的结果。

特征子空间

同一个特征值，对应的线性无关的特征向量，张成的空间。

秩与方程组的解

靠背的话容易记混，特别是齐次和非齐次分开记的时候。围绕增广矩阵的秩，统一的理解如下。
增广前的秩如果小于增广后的秩，说明会有这样的方程：0乘x1 + 0乘x2 = b，b不为0。这样就无解。
增广前后的秩如果相等，则有解。如果秩小于未知数个数（也就是列数），说明独立方程数量不够，有无穷多解。
如果秩等于列数，那就有唯一解。

拓展，单侧逆也可以在这里说。对于AX=b，
如果A列满秩，则A有左逆，X有唯一解，为A左逆乘b。
如果A行满秩，则A有右逆，X有解，如A右逆乘b。

参考文献

关于矩阵乘法结合律，使用了知乎@我心永恒的图。
还使用了知乎@toconscience的图。还有一些来源于网络。