Pytorch：目标检测网络-RetinaNet(不均衡样本问题)

Pytorch: 目标检测-样本不均衡问题-OHEM / Focol Loss(RetinaNet)

Copyright: Jingmin Wei, Pattern Recognition and Intelligent System, School of Artificial and Intelligence, Huazhong University of Science and Technology

Pytorch教程专栏链接

---

本教程不商用，仅供学习和参考交流使用，如需转载，请联系本人。

Reference

OHEM

Focol Loss(RetinaNet)

import torch
import torch.nn as nn
import torch.nn.functional as F

当前主流的物体检测算法，如 Faster RCNN 和 SSD 等，都是将物体检测当做分类问题来考虑，即先使用先验框或者 RPN 等生成感兴趣的区域，再对该区域进行分类与回归位置。这种基于分类思想的物体检测算法存在样本不均衡的问题，因而会降低模型的训练效率与检测精度。

本节首先分析样本不均衡带来的问题，随后会讲解两种经典的缓解不均衡问题的方法。

不均衡问题分析

在当前的物体检测算法中，由于检测算法各不相同，以及数据集之间的差异，可能会存在正负样本、难易样本、类别间样本这 $3$ 种不均衡问题。本节将详细分析这 $3$ 种不均衡问题的来源，以及常用的解决方法。

正负样本不均衡

以 Faster RCNN 为例，在 RPN 部分会生成 $20000$ 个左右的 Anchor，由于一张图中通常有 $10$ 个左右的物体，导致可能只有 $100$ 个左右的 Anchor 会是正样本，正负样本比例约为 $1:200$ ，存在严重的不均衡。

对于物体检测算法，有核心价值的是对应着真实物体的正样本，在训练时会根据其 loss 来调整网络参数。相比之下，负样本对应着图像的背景，如果有大量的负样本参与训练，则会淹没正样本的损失，从而降低网络收敛的效率与检测精度。

难易样本不均衡

除了正负样本，在物体检测中还存在着难易样本的不均衡问题。根据是否容易学习及与标签的重叠程度，可以将所有样本分为 $4$ 类：简单正样本(Easy Positive)、难正样本(Hard Positive)、简单负样本(Easy Negative)及难负样本(Hard Negative)，如图所示。

难样本指的是分类不太明确的边框，处在前景与背景的过渡区域上，在网络训练中难样本损失会较大，也是我们希望模型去学习优化的样本，利用这部分训练可以提升检测的准确率。

然而，大量的样本并非处在前景与背景的过渡区，而是与真实物体没有重叠区域的负样本，或者与真实物体重叠程度很高的正样本，这部分被称为简单样本，单个损失会较小，对参数收敛的作用有限。虽然简单样本单个损失小，但由于数量众多，因此如果全都计算损失的话，其损失也会比难样本大很多，这种难易样本的不均衡也会影响模型的收敛与精度。

值得注意的是，由于负样本中大量的是简单样本，导致难易样本与正负样本这两个不均衡问题有一定的重叠， 解决方法往往能同时对这两个问题起作用。

类别间样本不均衡

在有些物体检测的数据集中，还会存在类别间的不均衡问题。举个例子，数据集中有 $100$ 万个车辆、$1000$ 个行人的实例标签，样本比例为 $1000:1$ ，属于典型的类别不均衡。

这种情况下，如果不做任何处理，使用该数据集进行训练，由于行人这一类别可参考标签太少，会使得模型主要关注车这一类别的检测，网络中的参数主要根据车辆的损失进行优化，导致行人的检测精度大大下降。

解决方法

针对以上 $3$ 种不均衡问题，经典的物体检测算法在处理样本时，总体上有如下 $4$ 种缓解办法:

• Faster RCNN, SSD 等算法在正负样本的筛选时，根据样本与真实物体的 loU 大小，设置了 $3:1$ 的正负样本比例，这一点缓解了正负样本的不均衡，同时也对难易样本不均衡起到了作用。

• Faster RCNN 在 RPN 模块中，通过前景得分排序筛选出了 $2000$ 个左右的候选框，这也会将大量的负样本与简单样本过滤掉，缓解了前两个不均衡问题。

• 权重惩罚：对于难易样本与类别间的不均衡，可以增大难样本与少类别的损失权重，从而增大模型对这些样本的惩罚，缓解不均衡问题。

• 数据增强：从数据侧入手，可以在当前数据集上使用随机生成和添加扰动的方法，也可以利用网络爬虫数据等增加数据集的丰富性，从而缓解难易样本和类别间样本等不均衡问题，可以参考 SSD 的数据增强方法。

在线难样本挖掘: OHEM

针对难易样本不均衡的问题，$2016$ 年 CVPR 会议上的 OHEM(Online Hard Example Mining) 方法高效率地实现了在线难样本的挖掘，在多个数据集上都有着优越的表现，是一个很经典的难样本挖掘方法。

难样本挖据的思想最初在机器学习中被广泛使用，一般被称为难负样本挖掘(Hard Negaive Mining, HNM)，用于解决类别的不均衡问题。以SVMs(Support Vector Machines, 支持向量机)为例，HNM 方法先让模型收敛于当前的工作数据集，然后固定该模型，在数据集中去除简单的样本，添加些当前无法判断的样本，进行新的训练。这样的交替训练可以使得模型性能达到最优。

物体检测方法很难直接使用HNM算法进行挖掘。原因在于物体检测算法通常采用随机梯度下降(Stochastic Gradient Descent, SGD)等优化方法来进行优化，往往需要上万次的参数更新：而如果采用HNM交替训练的方法，每迭代几次就固定模型，训练的速度会大大下降。

OHEM 可以看做是 HNM 在物体检测算法上的应用，在实现时选择了 Fast RCNN 作为基础检测算法。Fast RCNN 与 Faster RCNN 类似，采用了两阶结构，在第二个阶段通过 RCNN 网络得到了边框的预测值，接下来使用了如下 $3$ 点标准来确定正、负样本。

• 当前 RoI 与真实物体的 IoU 大于 $0.5$ 时，判定为正样本。

• 当前 RoI 与真实物体的 IoU 大于 $0$ 且小于 $0.5$ 时，判定为负样本。

• 为了均衡正、负样本的数量，控制正、负样本的比例为 $1:3$ ，总数量不超过 $256$ 。通过这种方式有效缓解了正、负样本的不均衡。

上述方法虽然简单有效，但是容易忽略一些较为重要的难负样本，并且固定了正、负样本的比例与最大数量，显然不是最优的选择。以此为出发点，OHEM 将交替训练与 SGD 优化方法进行了结合，在每张图片的 RoI 中选择了较难的样本，实现了在线的难样本挖掘。

OHEM 实现在线难样本挖掘的网络如图所示。图中包含了两个相同的 RCNN 网络，上半部的 a 部分是只可读的网络，只进行前向运算；下半部的 b 网络即可读也可写，需要完成前向计算与反向传播。

在一个 batch 的训练中，基于 Fast RCNN 的 OHEM 算法可以分为以下 $5$ 步：

1. 按照原始 Fast RCNN 算法，经过卷积提取网络与 RoI Pooling 得到了每一张图像的 RoI。
2. 上半部的 a 网络对所有的 Rol 进行前向计算，得到每一个 Rol 的损失。
3. 对 RoI 的损失进行排序，进行一步 NMS 操作，以去除掉重叠严重的 RoI ,并在筛选后的 RoI 中选择出固定数量损失较大的部分，作为难样本。
4. 将筛选出的难样本输入到可读写的 b 网络中，进行前向计算，得到损失。
5. 利用 b 网络得到的反向传播更新网络，并将更新后的参数与上半部的 a 网络同步，完成一次迭代。

当然，为了实现方便，OHEM 也可以仅采用一个 RCNN 网络，在选择完难样本后将剩下的简单样本的损失置 $0$ ，可以起到相同的作用。但是，由于其特殊的损失计算方式，把简单的样本都舍弃了，导致模型无法提升对于简单样本的检测精度，这也是 OHEM 方法的一个弊端。

总体上，OHEM 是一个很经典的难样本挖掘 Trick，实现方式简单，可以显著提升网络训练的效率和检测性能，被广泛地应用于难样本的挖掘场景中，并且数据集越大、难度越高，OHEM 对于检测的提升越明显。

专注难样本: Focal Loss

当前一阶的物体检测算法，如 SSD 和 YOLO 等虽然实现了实时的速度，但精度始终无法与两阶的 Faster RCNN 相比。是什么阻碍了一阶算法的高精度呢？何凯明等人将其归咎于正、负样本的不均衡，并基于此提出了新的损失函数 Focal Loss 及网络结构 RetinaNet，在与同期一阶网络速度相同的前提下，其检测精度比同期最优的二阶网络还要高。

从前面的叙述中可以得知，Faster RCNN 在第一个阶段利用得分筛选出了 $2000$ 个左右的 RoI，可以过滤掉大部分的负样本，在第二个阶段通过固定正负样本比例或者 OHEM 等方法，可以有效解决正、负样本的不均衡问题。

而对于 SSD 等一阶网络，由于其需要直接从所有的预选框中进行筛选，即使使用了固定正、负样本比例的方法，仍然效率低下，简单的负样本仍然占据主要地位，导致其精度不如两阶网络。

为了解决一阶网络中样本的不均衡问题，何凯明等人首先改善了分类过程中的交叉熵函数，提出了可以动态调整权重的 Focal Loss 为了形成对比，接下来分别介绍标准交叉墒、平衡交叉熵及 Focal Loss。

标准交叉熵损失

首先回颇一下标准的交叉熵(Cross Etopy, CE)函数，其形式如下式所示。

$$CE(p,y)=\{\begin{array}{l}-\log (p)if(y=1)\\ -\log (1-p)otherwise\end{array}$$

公式中，$p$ 代表样本在该类别的预测概率，$y$ 代表样本标签。可以看出，当标签为 $1$ 时，$p$ 越接近 $1$ ，则损失越小；标签为$0$ 时 $p$ 越接近 $0$ ，则损失越小，符合优化的方向。

为了方便表示，按照下式将 $p$ 标记为 $p_t$

$$p_t=\{\begin{array}{l}pif(y=1)\\ 1-potherwise\end{array}$$

则交叉熵可以表示为下式的形式:

$$CE(p,y)=CE(p_t)=-\log (p_t)$$

标准的交叉熵中所有样本的权重都是相同的，因此如果正、负样本不均衡，大量简单的负样本会占据主导地位，少量的难样本与正样本会起不到作用，导致精度变差。

平衡交叉熵损失

为了改善样本的不平衡问题，平衡交叉熵在标准的基础上增加了一个系数 ${\alpha }_t$ ，来平衡正、负样本的权重，${\alpha }_t$ 由超参 $\alpha$ 按照下式计算得来，$\alpha$ 取值在 $[0,1]$ 区间内。

$${\alpha }_t=\{\begin{array}{l}\alpha if(y=1)\\ 1-\alpha otherwise\end{array}$$

有了 $\alpha$ ，平衡交叉熵损失公式如式所示。

$$CE(p_t)=-{\alpha }_t\log (p_t)$$

它即为 nn.CrossENtropyLoss 中的 weight 参数。

nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')

weight=None, # 是1维张量，包含n个元素，代表n类的权重，在训练样本不均衡时非常有用
ignore_index=-100, # 指定被忽略且对输入梯度没有贡献的目标值

尽管平衡交叉熵损失改善了正、负样本间的不平衡，但由于其缺乏对难易样本的区分，因此没有办法控制难易样本之间的不均衡。

专注难样本 Focal Loss

Focal Loss 为了同时调节正、负祥本与难易样本，提出了如下式所示的损失函数。
$$FL(p_t)=-{\alpha }_t(1-p_t{)}^{\gamma }\log (p_t)$$
对于该损失函数，有如下 $3$ 个属性：

• 与平衡交叉熵类似，引入了 ${\alpha }_t$ 权重，为了改善正负样本的不均衡，可以提升一些精度。

• $(1-p_t{)}^{\gamma }$ 是为了调节难易样本的权重。当一个边框被误分类时，$p_t$ 较小，则 $(1-p_t{)}^{\gamma }$ 接近于 $1$ 其损失几乎不受影响；当 $p_t$ 接近于 $1$ 时，表明其分类预测较好，是简单样本， $(1-p_t{)}^{\gamma }$ 接近于 $0$ ，因此其损失被调低了。

• $\gamma$ 是一个调制因子，$\gamma$ 越大，简单样本损失的贡献会越低。

RetinaNet

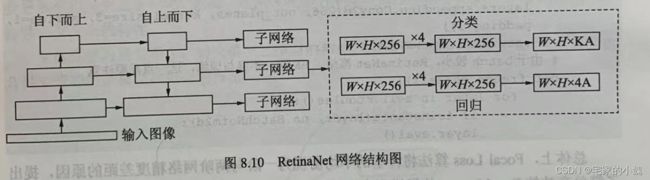
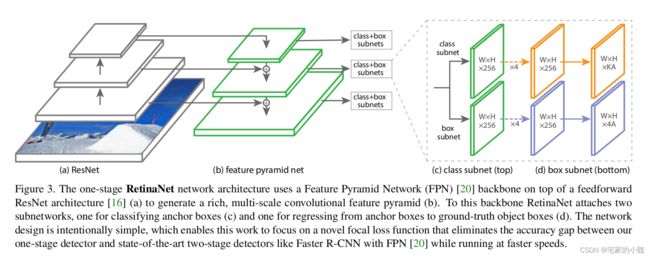
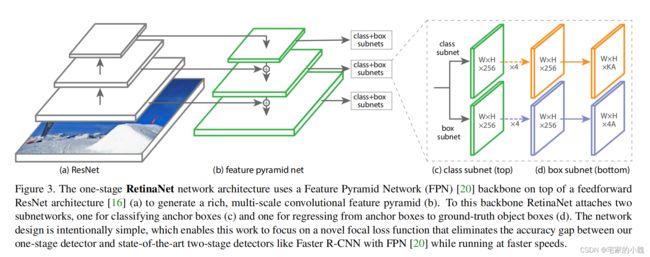
为了验证 Focal Loss 的效果，何凯明等人还提出了一个一阶物体检测结构 RetinaNet，结构如图所示。

对于 RetinaNet 的网络结构，有以下 $5$ 个细节:

• 在 Backbone 部分，RetinaNet 利用 ResNet 与 FPN 构建了一个多尺度特征的特征金字塔。

• RetinaNet 使用了类似于 Anchor 的预选框，在每一个金字塔层，使用了 $9$ 个大小不同的预选框。

• 分类子网络：分类子网络为每一个预选框预测其类别，因此其输出特征大小为 $KA\times W\times H$ ，$A$ 默认为 $9$ ，$K$ 代表类别数。中间使用全卷积网络与 ReLU 激活函数，最后利用 Sigmoid 函数输出预测值。

• 回归子网络：回归子网络与分类子网络平行，预测每一个预选框的偏移量，最终输出特征大小为 $4A\times W\times H$ 。与当前主流工作不同的是，两个子网络没有权重的共享。

• Focal Loss：与 OHEM 等方法不同，Focal Loss 在训练时作用到所有的预选框上。对于两个超参数，通常来讲，当 $\gamma$ 增大时，$\alpha$ 应当适当减小。实验中 $\gamma$ 取 $2$ ，$\alpha$ 取 $0.25$ 时效果最好。

代码实现

首先搭建 FPN 网络：

# 定义ResNet的Bottleneck类
class Bottleneck(nn.Module):
    expansion = 4 # 定义一个类属性，而非实例属性
    def __init__(self, in_channels, channels, stride=1, downsample=None):
        super(Bottleneck, self).__init__()
        # 网路堆叠层是由3个卷积+BN组成
        self.bottleneck = nn.Sequential(
            nn.Conv2d(in_channels, channels, 1, stride=1, bias=False),
            nn.BatchNorm2d(channels),
            nn.ReLU(True),
            nn.Conv2d(channels, channels, 3, stride=stride, padding=1, bias=False),
            nn.BatchNorm2d(channels),
            nn.ReLU(inplace=True),
            nn.Conv2d(channels, channels*self.expansion, 1, stride=1, bias=False),
            nn.BatchNorm2d(channels * self.expansion)
        )
        self.relu = nn.ReLU(inplace=True)

        # Down sample由一个包含BN的1*1卷积构成
        self.downsample = downsample

    def forward(self, x):
        identity = x 
        output = self.bottleneck(x)
        
        if self.downsample is not None:
            identity = self.downsample(x)
        # 将identity(恒等映射)与堆叠层输出相加
        output += identity
        output = self.relu(output)
        return output

# 定义FPN类，初始化需要一个list，代表ResNet每个阶段的Bottleneck的数量
class FPN(nn.Module):
    def __init__(self, layers):
        super(FPN, self).__init__()
        self.in_channels = 64
        # 处理输入的C1模块
        self.conv1 = nn.Conv2d(3, 64, 7, stride=2, padding=3, bias=False)
        self.bn1 = nn.BatchNorm2d(64)
        self.relu = nn.ReLU(inplace=True)
        self.maxpool = nn.MaxPool2d(3, stride=2, padding=1)
        # 搭建自下而上的C2,C3,C4,C5
        self.layer1 = self._make_layer(64, layers[0]) # stride=1
        self.layer2 = self._make_layer(128, layers[1], 2) # stride=2
        self.layer3 = self._make_layer(256, layers[2], 2) # stride=2
        self.layer4 = self._make_layer(512, layers[3], 2) # stride=2
        # 对C5减少通道数，得到M5
        self.toplayer = nn.Conv2d(2048, 256, 1, stride=1, padding=0)
        # 3*3卷积融合特征
        self.smooth1 = nn.Conv2d(256, 256, 3, 1, 1)
        self.smooth2 = nn.Conv2d(256, 256, 3, 1, 1)
        self.smooth3 = nn.Conv2d(256, 256, 3, 1, 1)
        # 横向连接，保证通道数相同
        self.latlayer1 = nn.Conv2d(1024, 256, 1, 1, 0)
        self.latlayer2 = nn.Conv2d(512, 256, 1, 1, 0)
        self.latlayer3 = nn.Conv2d(256, 256, 1, 1, 0)


    # 定义一个protected方法，构建C2-C5
    # 思想类似于ResNet，注意区分stride=1/2的情况
    def _make_layer(self, channels, blocks, stride=1):
        downsample = None
        # stride为2时，Residual Block存在恒等映射
        if stride != 1 or self.in_channels != Bottleneck.expansion * channels:
            downsample = nn.Sequential(
                nn.Conv2d(self.in_channels, Bottleneck.expansion*channels, 1, stride, bias=False),
                nn.BatchNorm2d(Bottleneck.expansion*channels)
            )
        layers = []
        layers.append(Bottleneck(self.in_channels, channels, stride, downsample))
        self.in_channels = channels*Bottleneck.expansion
        for i in range(1, blocks):
            layers.append(Bottleneck(self.in_channels, channels))
        return nn.Sequential(*layers)


    # 自上而下的上采样模块
    def _upsample_add(self, x, y):
        _, _, H, W = y.shape
        return F.interpolate(x, size=(H, W)) + y


    def forward(self, x):
        # 自下而上
        c1 = self.maxpool(self.relu(self.bn1(self.conv1(x))))
        c2 = self.layer1(c1)
        c3 = self.layer2(c2)
        c4 = self.layer3(c3)
        c5 = self.layer4(c4)
        # 自上而下
        m5 = self.toplayer(c5)
        m4 = self._upsample_add(m5, self.latlayer1(c4))
        m3 = self._upsample_add(m4, self.latlayer2(c3))
        m2 = self._upsample_add(m3, self.latlayer3(c2)) 
        # 卷积融合，平滑处理
        p5 = m5
        p4 = self.smooth1(m4)
        p3 = self.smooth2(m3)
        p2 = self.smooth3(m2)
        return p2, p3, p4, p5

def FPN50():
    return FPN([3, 4, 6, 3]) # FPN50

def FPN101():
    return FPN([3, 4, 23, 3]) # FPN101

def FPN152():
    return FPN([3, 8, 36, 3]) # FPN152

然后基于 FPN50 的基础网络，搭建一个 RetinaNet 。

class RetinaNet(nn.Module):
    num_anchors = 9 # 绑定类实例，默认使用9个Anchors
    
    def __init__(self, num_classes=20):
        super(RetinaNet, self).__init__()
        self.fpn = FPN50() # 引入FPN50，输出是大小不一的特征图
        self.num_classes = num_classes
        # 定位分支的输出是每个Anchor的4个边框位置
        self.loc_head = self._make_head(self.num_anchors*4)
        # 分类分支的输出是每个Anchor的20个类别得分
        self.cls_head = self._make_head(self.num_anchors*self.num_classes)

    # 定义protected方法，搭建分类和定位的分支
    def _make_head(self, out_planes):
        layers = []
        for _ in range(4):
            layers.append(nn.Conv2d(256, 256, 3, stride=1, padding=1))
            layers.append(nn.ReLU(True))
        layers.append(nn.Conv2d(256, out_planes, 3, stride=1, padding=1))
        return nn.Sequential(*layers)

    # 由于batch较小，RetinaNet冻结了BN层，不参与训练
    def freeze_bn(self):
        for layer in self.modules():
            if isinstance(layer, nn.BatchNorm2d):
                layer.eval()

    def forward(self, x):
        fms = self.fpn(x) # 首先获得Backbone的输出
        loc_preds = []
        cls_preds = []
        for fm in fms:
            # 对每个输出的特征图进行定位和分类分支运算
            loc_pred = self.loc_head(fm)
            cls_pred = self.cls_head(fm)
            # 通道维度变换，从[N,36,H,W]转变为[N,H*W*9,4]
            loc_pred = loc_pred.permute(0, 2, 3, 1).contiguous().view(x.size(0), -1, 4)
            # 通道维度变换，从[N,180,H,W]转变为[N,H*W*9,20]
            cls_pred = cls_pred.permute(0, 2, 3, 1).contiguous().view(x.size(0), -1, self.num_classes)
            # 将定位与分类分支的输出进行拼接，作为最终RetinaNet的输出
            loc_preds.append(loc_pred)
            cls_preds.append(cls_pred)
        return torch.cat(loc_preds, 1), torch.cat(cls_preds, 1)

retinanet = RetinaNet()

input = torch.randn(1, 3, 224, 224)
output = retinanet(input)

# 输出结果的大小
print(output[0].shape)
print(output[1].shape)

torch.Size([1, 37485, 4])
torch.Size([1, 37485, 20])

总体上，Focal Loss 算法将样本的不均衡视为一阶与两阶网络精度差距的原因，提出了简单高效的 Focal Loss ，使得模型专注于难样本上，并提出了一阶网络 RetinaNet ，实现了 SOTA 的精度。