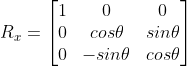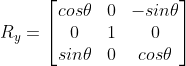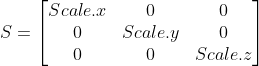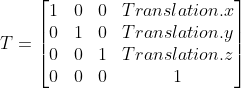详解坐标变换矩阵
在高级驾驶辅助系统(ADAS)领域,存在多种常用的坐标系:LiDAR坐标系、车辆坐标系、相机坐标系、图像坐标系等。在笔者最近的实习过程中,和这些坐标系频繁打交道。作为第一次在CSDN发文,本文将详细总结坐标变换矩阵。
目录
1. 何为坐标变换矩阵 (Transformation Matrix)
2. 旋转变换矩阵(Rotation Matrix)
3. 缩放变换矩阵(Scale Matrix)
4. 平移变换矩阵(Translation Matrix)
5. 综合变换
6. 小结
1. 何为坐标变换矩阵 (Transformation Matrix)
首先要回答一个问题,何为坐标变换矩阵呢?
“横看成岭侧成峰,远近高低各不同”,这说明了参照系的选取对我们观察事物的重要性。在以上所举例的坐标系变换的语境下,点是客观存在的,而坐标系则是根据不同的应用场景人为选择的。处理pcd点云数据时,需要三维的LiDAR坐标系;查看图像时,需要二维的图像坐标系(通常为1920*1080等尺寸)。即:
“点不变,坐标系进行变换。”
而坐标变换矩阵,就是在这种变换坐标系的前后,点的数值的变换映射关系矩阵。注意,点不动,坐标系动。下文讨论三种变换矩阵:旋转变换矩阵、缩放变换矩阵和平移变换矩阵。
2. 旋转变换矩阵(Rotation Matrix)
2.1 二维情形
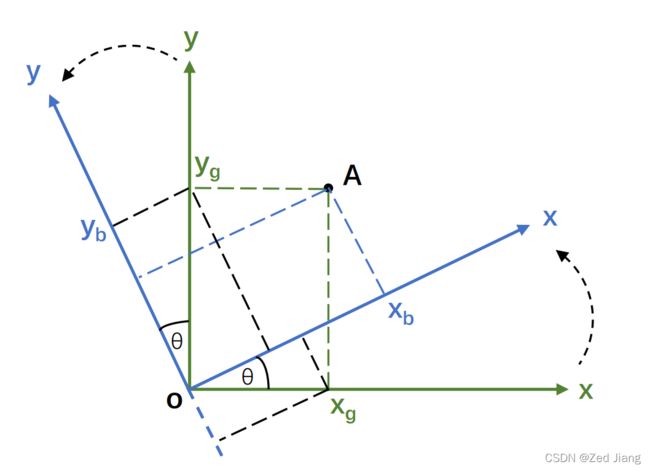
如图1所示,在二维平面xoy上,由绿色坐标系逆时针旋转θ°到蓝色坐标系。可以看到,点A是没有移动的,变化的是点A分别在前后两个坐标系中的坐标,即从![]() 变换到了
变换到了![]() 。
。
如图1中黑色虚线的分解方式所示,通过矢量分解(类似于物理中力、速度等矢量的分解),将绿色坐标系中的![]() 分别分解到蓝色坐标系的x轴和y轴上,可以得到:
分别分解到蓝色坐标系的x轴和y轴上,可以得到:
用矩阵表示为:
其中R则为二维情形下的旋转变换矩阵,它表示了A点在前后坐标系中的值的映射关系。
2.2 三维情形
有了上述在二维平面旋转的基础,三维空间的旋转矩阵也就不难得出了。
即绕x轴,y轴,z轴分别进行旋转。最后将这三个旋转变换矩阵相乘,就能得到在三维空间任意角度的旋转变换矩阵了。(xyz轴满足右手系关系)
在绕x轴旋转的时候,可以看作在yoz二维平面上的旋转,此时x的值不变。
在绕y轴旋转的时候,可以看作在zox二维平面上的旋转,此时y的值不变。
在绕z轴旋转的时候,可以看作在xoy二维平面上的旋转,此时z的值不变。
最终的三维旋转变换矩阵就是上面三个矩阵相乘,意为三维坐标系分别绕x轴、y轴和z轴旋转相应的角度。
2.3 顺时针?逆时针?
在笔者初次接触旋转概念之时,常常对何时顺时针,何时逆时针十分头疼。
高中就接触到点的旋转矩阵R(rotation matrix of a point),在这种情况下是坐标系不变,点绕坐标原点顺时针旋转 θ°。
而在本文的情形下,旋转变换矩阵的形式完全一致,但是方向却相反了——变成了逆时针!究其原因,还是上文老生常谈的那点,高中的矩阵是点动系不动,而本文是系动点不动。因此方向正好相反了。
回到本文的系动点不动,此时再从两种角度推导出顺时针旋转的公式。
1)θ变为-θ:此时就是选择了相反的旋转角度,变成顺时针。
2)求原矩阵的逆矩阵:先逆时针,再顺时针,相当于回到原系,也就是坐标和单位矩阵相乘。
可以得到,坐标系顺时针旋转θ°的旋转变换矩阵为:
3. 缩放变换矩阵(Scale Matrix)
除了旋转变换,还有坐标数值的纯粹放大缩小变换,即缩放变换。下面直接给出缩放变换的公式:
上式中点的x, y, z坐标值分别扩大(缩小)了Scale.x, Scale.y, Scale.z倍。
缩放矩阵同样存在“系动点不动”还是“点动系不动”的问题。如果是“点动系不动”,那么S矩阵中的Scale.x, Scale.y, Scale.z就是单纯的点x, y, z的扩大(缩小)倍数。
如果是本文重点探讨的“系动点不动”,那么S矩阵中的Scale.x, Scale.y, Scale.z就是坐标系的x, y, z轴的单位扩大(缩小)倍数的倒数。换言之,如果坐标轴单位放大Scale倍,那么点x, y, z的值就要缩小Scale倍。可以用千米和米的转换来思考这个问题。如果单位是m,一个物体长1000m。当单位变为km后,这个物体就长1km了。单位扩大的同时,数值上从1000缩小为了1。
4. 平移变换矩阵(Translation Matrix)
坐标系的旋转和缩放可以通过3*3的变换矩阵完成,但是平移就需要将3*3扩展到4*4,引入齐次变换矩阵。下面直接给出平移变换矩阵的公式:
具体过程即:
平移矩阵同样存在“系动点不动”还是“点动系不动”的问题。
如果是本文重点探讨的“系动点不动”。如果系向左(x轴负方向)/后(y轴负方向)/下(z轴负方向)平移,那么T矩阵中的Translation.x, Translation.y, Translation.z为正;如果系向右(x轴正方向)/前(y轴正方向)/上(z轴正方向)平移,那么T矩阵中的Translation.x, Translation.y, Translation.z为负。可以借助爬楼梯来理解,小明在地面抬头看着5楼,五楼相当于+5。当小明爬到5楼的时候,此时五楼相当于0了。小明爬到10楼的时候,此时五楼就相当于-5了。小明就是坐标系的原点,5楼就是不动的一个点。
5. 综合变换
将变换矩阵和点向量全部齐次化:
![]()
那么此时,对于不动点,如果按照“旋转-缩放-平移”的顺序变换坐标系后,此点的值产生如下变换:
![]()
6. 小结
ADAS中涉及多种坐标系的变换,点的坐标会随着坐标系的变换而变化。坐标变换矩阵就是在坐标系变换前后,点的数值的映射关系矩阵。主要有旋转变换矩阵、缩放变换矩阵和平移变换矩阵等。极其重要和容易混淆的是,在具体的应用场景中,是什么在变,什么不变,是系还是点。矩阵的具体实现可以采用python中的numpy模块。