【数学建模】层次分析（Matlab&Python代码实现）

目录

1 概述

2 AHP的基本步骤

 3 简单入门算例

4 升级入门算例

4.1 算例

4.2 Matlab代码实现

5 Python代码实现

---

1 概述

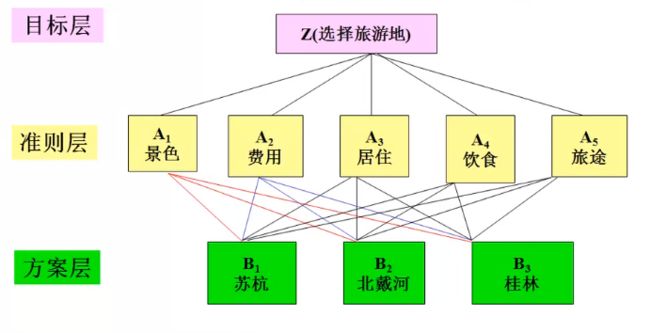
适用于解决多个备选方案决策以及在选择过程中各个因素的重要性比较，比如要选择旅游地，有3个选择方案，苏杭、北戴河和桂林。选择过程需要考虑多个因素，比如景色、费用、居住、饮食和旅途。

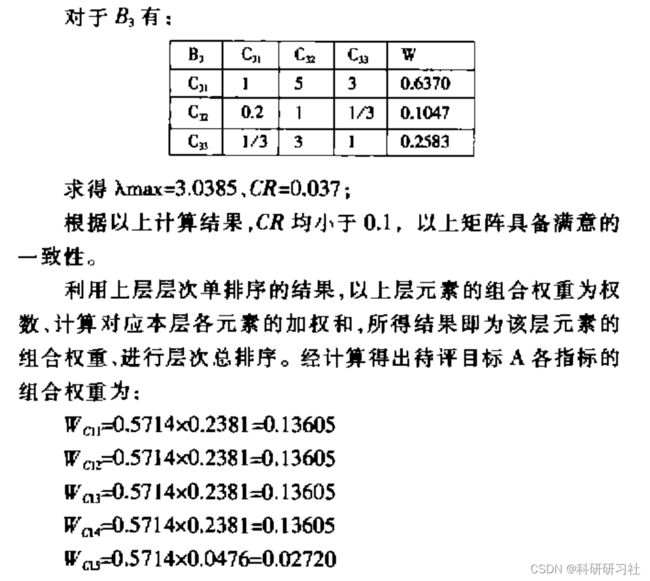
AHP对人们的主观判断加以形式化地表达和处理,逐步剔除主观性,从而尽可能地转化成客观描述。其正确与成功.取决于客观成分能否达到足够合理的地步。由于理论研究的遍历与工程实现的采样之间总是存在着(或大或小,往往又是巨大的}差距.在借助于判断矩阵计算出相对权重后，欲克服两两相比未能穷尽的不足,对判断矩阵做一致性检验,成为不可或缺的环节。

2 AHP的基本步骤

运用AHP方法解决问题,大体可按如下步骤进行:

1）将问题分解.建立层次结构;
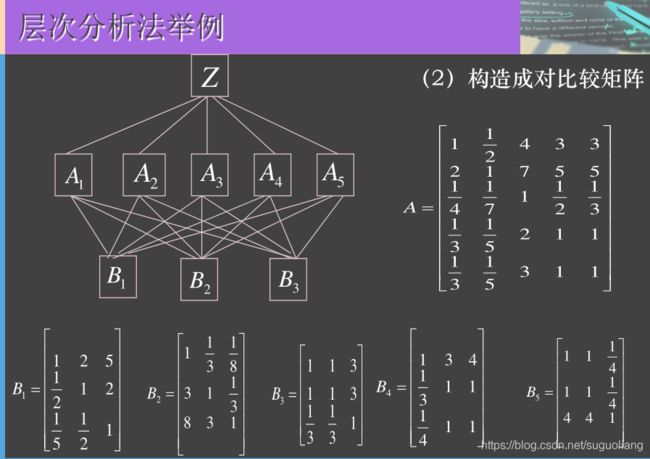
2）构造两两比较判断矩阵:
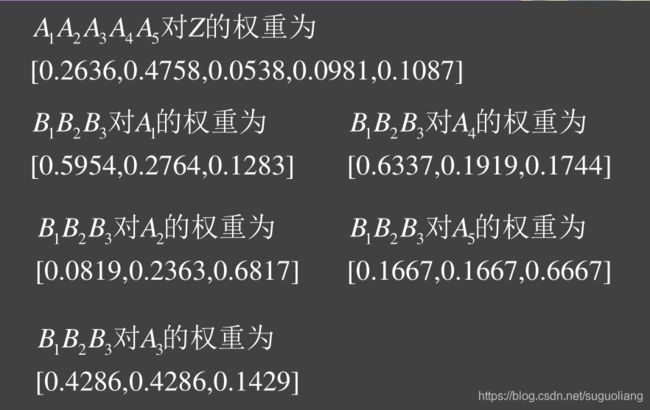
3）由判断矩阵计算比较元素的相对权重:

4）计算各层元素的组合权重。

现举例说明上述过程。 

 

 3 简单入门算例

参考：(1条消息) 层次分析法详解（matlab）_黑脉金的博客-CSDN博客_层次分析法matlab程序

 

4 升级入门算例

4.1 算例

 银行在国家经济社会发展过程中扮演者重要的决策，银行的破产会对企业和个人造成众多不利的影响。相比国内的银行，国际银行的倒闭频次更高，因此国际银行倒闭原因的分析与预测受到众多管理者与学术研究者的广泛关注。附件1中提供了波兰2017年至2021年的现存或倒闭银行的64项指标数据，各项数据指标具有对应的解释。

请你从这64项数据中整理出适合的投入产出数据，并对各银行的效率展开对应评价，同时提供银行倒闭效率的分界线;

 思路：使用二分类的类值

• ·0 - 在预测期内没有破产的公司
• 1 - 破产公司

4.2 Matlab代码实现

clear
clc
%% 加载数据
%load data.txt
load data.txt
X=data(:,3:end); %第一列和第二列：X1净利润/总资产 ；X2 总负债/总资产
%% 归一化
X=mapminmax(X',0,1)';
mapping.mean = mean(X, 1);
C = cov(X);%协方差矩阵
C(isnan(C)) = 0;
C(isinf(C)) = 0;
[M, lambda] = eig(C);%求C矩阵特征向量及特征值
[lambda, ind] = sort(diag(lambda), 'descend');%排序
lambda=lambda./sum(lambda);%特征值归一化
a=lambda;
lambda=cumsum(lambda);%累计贡献率
mapping.lambda = lambda;
M=M(:,ind);
Z=[];
A=[];
%% 第一列和第二列净利润/总资产 ；X2 总负债/总资产
for i=1:size(M,2)
    [~,z]=max(abs(M(:,i)));
    if length(find(Z==z))==0
        Z=[Z,z];
        A=[A,a(i)];
    end
end
%% 五年
Z=Z(1:5);
W=A(1:5)./sum(A(1:5));

%% 确定主要指标
disp('主要指标序号')
disp(Z)%指标序号
disp('权重')
disp(W)
%% 评价值
P=[data(:,1:2),X(:,Z)*W'];

%检验
disp('整体在预测期内没有破产的公司和破产公司的分别求平均值')
[mean(P(find(P(:,2)==0),3)),mean(P(find(P(:,2)==1),3))]
disp('2017年在预测期内没有破产的公司和破产公司的分别求平均值')
[mean(P(find(P(find(P(:,2)==0),1)==2017),3)),mean(P(find(P(find(P(:,2)==1),1)==2017),3))]
disp('2018年在预测期内没有破产的公司和破产公司的分别求平均值')
[mean(P(find(P(find(P(:,2)==0),1)==2018),3)),mean(P(find(P(find(P(:,2)==1),1)==2018),3))]
disp('2019年在预测期内没有破产的公司和破产公司的分别求平均值')
[mean(P(find(P(find(P(:,2)==0),1)==2019),3)),mean(P(find(P(find(P(:,2)==1),1)==2019),3))]
disp('20120年在预测期内没有破产的公司和破产公司的分别求平均值')
[mean(P(find(P(find(P(:,2)==0),1)==2020),3)),mean(P(find(P(find(P(:,2)==1),1)==2020),3))]
disp('2021年在预测期内没有破产的公司和破产公司的分别求平均值')
[mean(P(find(P(find(P(:,2)==0),1)==2021),3)),mean(P(find(P(find(P(:,2)==1),1)==2021),3))]


%检验通过后，接下来就是求分界线，其实就是依次分类统计下均值在取个中间值就好了
%求每个主要指标的
M=[];
for i=1:length(Z);
    M(i,:)=[mean(X(find(data(:,2)==0),Z(i))),mean(X(find(data(:,2)==1),Z(i)))];
end
disp('主要指标分界点')
M=mean(M,2)

数据和代码放不下，点这里下载：主成层份分析

 结果：

主要指标序号
    29    33    34     3    16

权重
    0.6047    0.1617    0.1008    0.0720    0.0608

整体class=0和1的分别求平均值

ans =

    0.4434    0.4181

2017年class=0和1的分别求平均值

ans =

    0.4503    0.4703

2018年class=0和1的分别求平均值

ans =

    0.4464    0.4689

2019年class=0和1的分别求平均值

ans =

    0.4362    0.4706

20120年class=0和1的分别求平均值

ans =

    0.4371    0.4543

2021年class=0和1的分别求平均值

ans =

    0.4502    0.4360

主要指标分界点

M =

    0.5462
    0.0411
    0.1593
    0.8765
    0.2415

>> 

本部分来源于我的男神川川，参考链接点这里：川川

5 Python代码实现

import numpy as np
class AHP:
    """
    相关信息的传入和准备
    """

    def __init__(self, array):
        ## 记录矩阵相关信息
        self.array = array
        ## 记录矩阵大小
        self.n = array.shape[0]
        # 初始化RI值，用于一致性检验
        self.RI_list = [0, 0, 0.52, 0.89, 1.12, 1.26, 1.36, 1.41, 1.46, 1.49, 1.52, 1.54, 1.56, 1.58,
                        1.59]
        # 矩阵的特征值和特征向量
        self.eig_val, self.eig_vector = np.linalg.eig(self.array)
        # 矩阵的最大特征值
        self.max_eig_val = np.max(self.eig_val)
        # 矩阵最大特征值对应的特征向量
        self.max_eig_vector = self.eig_vector[:, np.argmax(self.eig_val)].real
        # 矩阵的一致性指标CI
        self.CI_val = (self.max_eig_val - self.n) / (self.n - 1)
        # 矩阵的一致性比例CR
        self.CR_val = self.CI_val / (self.RI_list[self.n - 1])

    """
    一致性判断
    """

    def test_consist(self):
        # 打印矩阵的一致性指标CI和一致性比例CR
        print("判断矩阵的CI值为：" + str(self.CI_val))
        print("判断矩阵的CR值为：" + str(self.CR_val))
        # 进行一致性检验判断
        if self.n == 2:  # 当只有两个子因素的情况
            print("仅包含两个子因素，不存在一致性问题")
        else:
            if self.CR_val < 0.1:  # CR值小于0.1，可以通过一致性检验
                print("判断矩阵的CR值为" + str(self.CR_val) + ",通过一致性检验")
                return True
            else:  # CR值大于0.1, 一致性检验不通过
                print("判断矩阵的CR值为" + str(self.CR_val) + "未通过一致性检验")
                return False

    """
    算术平均法求权重
    """

    def cal_weight_by_arithmetic_method(self):
        # 求矩阵的每列的和
        col_sum = np.sum(self.array, axis=0)
        # 将判断矩阵按照列归一化
        array_normed = self.array / col_sum
        # 计算权重向量
        array_weight = np.sum(array_normed, axis=1) / self.n
        # 打印权重向量
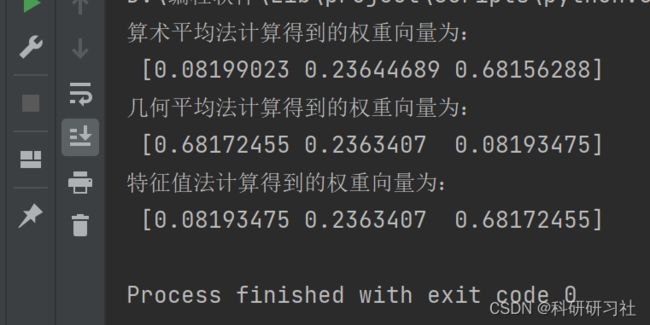
        print("算术平均法计算得到的权重向量为：\n", array_weight)
        # 返回权重向量的值
        return array_weight

    """
    几何平均法求权重
    """

    def cal_weight__by_geometric_method(self):
        # 求矩阵的每列的积
        col_product = np.product(self.array, axis=0)
        # 将得到的积向量的每个分量进行开n次方
        array_power = np.power(col_product, 1 / self.n)
        # 将列向量归一化
        array_weight = array_power / np.sum(array_power)
        # 打印权重向量
        print("几何平均法计算得到的权重向量为：\n", array_weight)
        # 返回权重向量的值
        return array_weight

    """
    特征值法求权重
    """

    def cal_weight__by_eigenvalue_method(self):
        # 将矩阵最大特征值对应的特征向量进行归一化处理就得到了权重
        array_weight = self.max_eig_vector / np.sum(self.max_eig_vector)
        # 打印权重向量
        print("特征值法计算得到的权重向量为：\n", array_weight)
        # 返回权重向量的值
        return array_weight


if __name__ == "__main__":
    # 给出判断矩阵
    b = np.array([[1, 1 / 3, 1 / 8], [3, 1, 1 / 3], [8, 3, 1]])

    # 算术平均法求权重
    weight1 = AHP(b).cal_weight_by_arithmetic_method()
    # 几何平均法求权重
    weight2 = AHP(b).cal_weight__by_geometric_method()
    # 特征值法求权重
    weight3 = AHP(b).cal_weight__by_eigenvalue_method()